Chapter 2: Convex analysis (Part 2)

Dr. Le Hai Yen

Institute of Mathematics, VAST, Hanoi

2022

Chapter 2: Convex analysis (Part 2) 1 / 28

 Convex sets

Table of contents

1 Convex sets

2 Convex functions
Definition and Examples
First Order Characterizations of Convex Functions
Second Order Characterization of Convex Functions
Operations Preserving Convexity
Continuity and Differentiability of Convex Functions

Chapter 2: Convex analysis (Part 2) 2 / 28

 Convex functions

Table of contents

1 Convex sets

2 Convex functions
Definition and Examples
First Order Characterizations of Convex Functions
Second Order Characterization of Convex Functions
Operations Preserving Convexity
Continuity and Differentiability of Convex Functions

Chapter 2: Convex analysis (Part 2) 3 / 28

 Convex functions Definition and Examples

Definition 2.26
A function f : Rn → R ∪ {+∞} is said to be convex when, for all
x, y ∈ Rn and all λ ∈ [0, 1], there holds

f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ). (1)

Chapter 2: Convex analysis (Part 2) 4 / 28

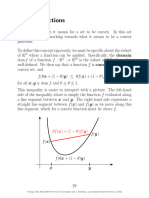
 Convex functions Definition and Examples

Chapter 2: Convex analysis (Part 2) 5 / 28

 Convex functions Definition and Examples

Example 2.27:

1. The affine function f (x) = aT x + b, where a ∈ Rn and b ∈ R is

convex.
2. The norm function f (x) = ∥x∥ is convex.

Chapter 2: Convex analysis (Part 2) 6 / 28

 Convex functions Definition and Examples

Example 2.27:

1. The affine function f (x) = aT x + b, where a ∈ Rn and b ∈ R is

convex.
2. The norm function f (x) = ∥x∥ is convex.

Chapter 2: Convex analysis (Part 2) 6 / 28

 Convex functions Definition and Examples

Definition 2.28:
Let f : Rn → R ∪ {+∞}. The domain (or effective domain) of f is the
nonempty set
domf := {x ∈ Rn | f (x) < +∞}.

Definition 2.29:
Given f : Rn → R ∪ {+∞}, not identically equal to +∞, the epigraph of
f is the nonempty set

epif := {(x, r ) ∈ Rn × R| r ≥ f (x)}.

Chapter 2: Convex analysis (Part 2) 7 / 28

 Convex functions Definition and Examples

Definition 2.28:
Let f : Rn → R ∪ {+∞}. The domain (or effective domain) of f is the
nonempty set
domf := {x ∈ Rn | f (x) < +∞}.

Definition 2.29:
Given f : Rn → R ∪ {+∞}, not identically equal to +∞, the epigraph of
f is the nonempty set

epif := {(x, r ) ∈ Rn × R| r ≥ f (x)}.

Chapter 2: Convex analysis (Part 2) 7 / 28

 Convex functions Definition and Examples

Epigraph

Chapter 2: Convex analysis (Part 2) 8 / 28

 Convex functions Definition and Examples

Proposition 2.30:
Let f : Rn → R ∪ {+∞} be not identically equal to +∞,. The following
properties are equivalent:
(i) f is convex;
(ii) its epigraph is a convex set in Rn × R;

Proof.

Chapter 2: Convex analysis (Part 2) 9 / 28

 Convex functions Definition and Examples

Proposition 2.30:
Let f : Rn → R ∪ {+∞} be not identically equal to +∞,. The following
properties are equivalent:
(i) f is convex;
(ii) its epigraph is a convex set in Rn × R;

Proof.

Chapter 2: Convex analysis (Part 2) 9 / 28

 Convex functions Definition and Examples

Proposition 2.30:
Let f : Rn → R ∪ {+∞} be not identically equal to +∞,. The following
properties are equivalent:
(i) f is convex;
(ii) its epigraph is a convex set in Rn × R;

Proof.

Chapter 2: Convex analysis (Part 2) 9 / 28

 Convex functions Definition and Examples

Definition 2.31:
Let C be a nonempty convex set in Rn . A function f : C → R is said to
be convex on C when, for all x, y ∈ C and all λ ∈ [0, 1], it holds

f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ). (2)

We say that f is strictly convex on C if (2) holds as a strict inequality if

x ̸= y and 0 < λ < 1. The function f is said to be strongly convex on C
if there exists c > 0 such that
1
f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ) − cλ(1 − λ)∥x − y ∥2
2
for all x, y ∈ C and all λ ∈ [0, 1].

Chapter 2: Convex analysis (Part 2) 10 / 28

 Convex functions Definition and Examples

Definition 2.31:
Let C be a nonempty convex set in Rn . A function f : C → R is said to
be convex on C when, for all x, y ∈ C and all λ ∈ [0, 1], it holds

f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ). (2)

We say that f is strictly convex on C if (2) holds as a strict inequality if

x ̸= y and 0 < λ < 1. The function f is said to be strongly convex on C
if there exists c > 0 such that
1
f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ) − cλ(1 − λ)∥x − y ∥2
2
for all x, y ∈ C and all λ ∈ [0, 1].

Chapter 2: Convex analysis (Part 2) 10 / 28

 Convex functions Definition and Examples

Definition 2.31:
Let C be a nonempty convex set in Rn . A function f : C → R is said to
be convex on C when, for all x, y ∈ C and all λ ∈ [0, 1], it holds

f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ). (2)

We say that f is strictly convex on C if (2) holds as a strict inequality if

x ̸= y and 0 < λ < 1. The function f is said to be strongly convex on C
if there exists c > 0 such that
1
f (λx + (1 − λ)y ) ≤ λf (x) + (1 − λ)f (y ) − cλ(1 − λ)∥x − y ∥2
2
for all x, y ∈ C and all λ ∈ [0, 1].

Chapter 2: Convex analysis (Part 2) 10 / 28

 Convex functions Definition and Examples

Proposition 2.32:
The function f is strongly convex with modulus c if and only if the
function f − c2 ∥.∥2 is convex .

Proof.

Chapter 2: Convex analysis (Part 2) 11 / 28

 Convex functions Definition and Examples

Jensen’s inequality

Theorem 2.33:
Let f : C → R be a convex function where C ⊆ Rn is a convex set. Then
for any x1 , . . . , xk ∈ C and λ ∈ △k , the following inequality holds:

Xk k
X
f( λi xi ) ≤ λi f (xi ). (3)
i=1 i=1

Proof.

Chapter 2: Convex analysis (Part 2) 12 / 28

 Convex functions First Order Characterizations of Convex Functions

Theorem 2.34:
Let f : Rn → R and C be a convex set in Rn . Assume that f is
continuously differentiable on an open set containing C . Then f is convex
on C if and only if

f (x) + ∇f (x)T (y − x) ≤ f (y ) ∀x, y ∈ C . (4)

Proof.

Chapter 2: Convex analysis (Part 2) 13 / 28

 Convex functions First Order Characterizations of Convex Functions

Theorem 2.35:
Let f : Rn → R and C be a convex set in Rn . Assume that f is
continuously differentiable on an open set containing C . Then f is strictly
convex over C if and only if

f (x) + ∇f (x)T (y − x) < f (y ) ∀x ̸= y ∈ C . (5)

Theorem 2.36:
Let f : Rn → R be the quadratic function given by
f (x) = x T Ax + 2b T x + c, where A ∈ Rn×n is symmetric, b ∈ Rn , and
c ∈ R. Then f is (strictly) convex if and only if A is positive semi-definite
(positive definite).

Chapter 2: Convex analysis (Part 2) 14 / 28

 Convex functions First Order Characterizations of Convex Functions

Theorem 2.35:
Let f : Rn → R and C be a convex set in Rn . Assume that f is
continuously differentiable on an open set containing C . Then f is strictly
convex over C if and only if

f (x) + ∇f (x)T (y − x) < f (y ) ∀x ̸= y ∈ C . (5)

Theorem 2.36:
Let f : Rn → R be the quadratic function given by
f (x) = x T Ax + 2b T x + c, where A ∈ Rn×n is symmetric, b ∈ Rn , and
c ∈ R. Then f is (strictly) convex if and only if A is positive semi-definite
(positive definite).

Chapter 2: Convex analysis (Part 2) 14 / 28

 Convex functions First Order Characterizations of Convex Functions

Examples of convex and nonconvex quadratic functions are illustrated in

Figure 1.

(b) Noncovex quadratic function

(a) Convex quadratic function

Figure: Source:
https://www.quora.com/Are-all-quadratic-programming-problems-convex

Chapter 2: Convex analysis (Part 2) 15 / 28

 Convex functions First Order Characterizations of Convex Functions

Monotonicity of gradient

Theorem 2.37
Let f : Rn → R and C be a convex set in Rn . Assume that f is
continuously differentiable on an open set containing C . Then f is convex
over C if and only if

(∇f (x) − ∇f (y ))T (x − y ) ≥ 0 ∀x, y ∈ C . (6)

Proof.

Chapter 2: Convex analysis (Part 2) 16 / 28

 Convex functions Second Order Characterization of Convex Functions

Second order characterization of convexity

Theorem 2.38:
Let f : Rn → R and C be an open convex set in Rn . Assume that f is
tiwce continuously differentiable on C . Then f is convex if and only if
∇2 f (x) ⪰ 0 for any x ∈ C .

Proof.

Theorem 2.39:
Let f : Rn → R and C be an open convex set in Rn . Assume that f is
tiwce continuously differentiable on C , and suppose that ∇2 f (x) ≻ 0 for
any x ∈ C . Then f is strictly convex over C .

Proof.

Chapter 2: Convex analysis (Part 2) 17 / 28

 Convex functions Second Order Characterization of Convex Functions

Second order characterization of convexity

Theorem 2.38:
Let f : Rn → R and C be an open convex set in Rn . Assume that f is
tiwce continuously differentiable on C . Then f is convex if and only if
∇2 f (x) ⪰ 0 for any x ∈ C .

Proof.

Theorem 2.39:
Let f : Rn → R and C be an open convex set in Rn . Assume that f is
tiwce continuously differentiable on C , and suppose that ∇2 f (x) ≻ 0 for
any x ∈ C . Then f is strictly convex over C .

Proof.

Chapter 2: Convex analysis (Part 2) 17 / 28

 Convex functions Second Order Characterization of Convex Functions

Second order characterization of convexity

Theorem 2.38:
Let f : Rn → R and C be an open convex set in Rn . Assume that f is
tiwce continuously differentiable on C . Then f is convex if and only if
∇2 f (x) ⪰ 0 for any x ∈ C .

Proof.

Theorem 2.39:
Let f : Rn → R and C be an open convex set in Rn . Assume that f is
tiwce continuously differentiable on C , and suppose that ∇2 f (x) ≻ 0 for
any x ∈ C . Then f is strictly convex over C .

Proof.

Chapter 2: Convex analysis (Part 2) 17 / 28

 Convex functions Second Order Characterization of Convex Functions

Example 2.40:
The log-sum-exp function f (x) = ln(e x1 + e x2 + · · · + e xn ) for
x = (x1 , x2 , . . . , xn ) is convex on Rn .
x12
The quadratic-over-linear function f (x) = x2 is convex on
{x = (x1 , x2 )| x2 > 0}.

Chapter 2: Convex analysis (Part 2) 18 / 28

 Convex functions Second Order Characterization of Convex Functions

Example 2.40:
The log-sum-exp function f (x) = ln(e x1 + e x2 + · · · + e xn ) for
x = (x1 , x2 , . . . , xn ) is convex on Rn .
x12
The quadratic-over-linear function f (x) = x2 is convex on
{x = (x1 , x2 )| x2 > 0}.

Chapter 2: Convex analysis (Part 2) 18 / 28

 Convex functions Second Order Characterization of Convex Functions

Example 2.40:
The log-sum-exp function f (x) = ln(e x1 + e x2 + · · · + e xn ) for
x = (x1 , x2 , . . . , xn ) is convex on Rn .
x12
The quadratic-over-linear function f (x) = x2 is convex on
{x = (x1 , x2 )| x2 > 0}.

Chapter 2: Convex analysis (Part 2) 18 / 28

 Convex functions Operations Preserving Convexity

Preservation of convexity under summation and

multiplication by non-negative scalars

Theorem 2.41
(i) Let f be a convex function defined over a convex set C ⊆ Rn and let
α ≥ 0. Then αf is a convex function over C .
(ii) Let f1 , f2 , . . . , fp be convex functions over a convex set C ⊆ Rn . Then
the sum function f1 + f2 + . . . + fp is convex over C .

Proof.

Chapter 2: Convex analysis (Part 2) 19 / 28

 Convex functions Operations Preserving Convexity

Preservation of convexity under summation and

multiplication by non-negative scalars

Theorem 2.41
(i) Let f be a convex function defined over a convex set C ⊆ Rn and let
α ≥ 0. Then αf is a convex function over C .
(ii) Let f1 , f2 , . . . , fp be convex functions over a convex set C ⊆ Rn . Then
the sum function f1 + f2 + . . . + fp is convex over C .

Proof.

Chapter 2: Convex analysis (Part 2) 19 / 28

 Convex functions Operations Preserving Convexity

Preservation of convexity under summation and

multiplication by non-negative scalars

Theorem 2.41
(i) Let f be a convex function defined over a convex set C ⊆ Rn and let
α ≥ 0. Then αf is a convex function over C .
(ii) Let f1 , f2 , . . . , fp be convex functions over a convex set C ⊆ Rn . Then
the sum function f1 + f2 + . . . + fp is convex over C .

Proof.

Chapter 2: Convex analysis (Part 2) 19 / 28

 Convex functions Operations Preserving Convexity

Preservation of convexity under linear change of variables

Theorem 2.42
Let f : C → R be a convex function defined on a convex set C ⊆ Rn . Let
A ∈ Rn×m and b ∈ Rn . Then the function g defined by

g (y ) = f (Ay + b)

is convex over the convex set D = {y ∈ Rm | Ay + b ∈ C }.

Proof.

Example 2.43:(Generalized quadratic-over-linear)

Let A ∈ Rn×m , b ∈ Rm , c ∈ Rn , and d ∈ R. We assume that c ̸= 0. The
quadratic-over-linear function
∥Ax + b∥2
g (x) =
cT x + d
Chapter 2: Convex analysis (Part 2) 20 / 28
 Convex functions Operations Preserving Convexity

Preservation of convexity under linear change of variables

Theorem 2.42
Let f : C → R be a convex function defined on a convex set C ⊆ Rn . Let
A ∈ Rn×m and b ∈ Rn . Then the function g defined by

g (y ) = f (Ay + b)

is convex over the convex set D = {y ∈ Rm | Ay + b ∈ C }.

Proof.

Example 2.43:(Generalized quadratic-over-linear)

Let A ∈ Rn×m , b ∈ Rm , c ∈ Rn , and d ∈ R. We assume that c ̸= 0. The
quadratic-over-linear function
∥Ax + b∥2
g (x) =
cT x + d
Chapter 2: Convex analysis (Part 2) 20 / 28
 Convex functions Operations Preserving Convexity

Preservation of convexity under linear change of variables

Theorem 2.42
Let f : C → R be a convex function defined on a convex set C ⊆ Rn . Let
A ∈ Rn×m and b ∈ Rn . Then the function g defined by

g (y ) = f (Ay + b)

is convex over the convex set D = {y ∈ Rm | Ay + b ∈ C }.

Proof.

Example 2.43:(Generalized quadratic-over-linear)

Let A ∈ Rn×m , b ∈ Rm , c ∈ Rn , and d ∈ R. We assume that c ̸= 0. The
quadratic-over-linear function
∥Ax + b∥2
g (x) =
cT x + d
Chapter 2: Convex analysis (Part 2) 20 / 28
 Convex functions Operations Preserving Convexity

Theorem 2.44:
Let f : C → R be a convex function over the convex set C ⊆ Rn . Let
g : I → R be a one-dimensional nondecreasing convex function over the
interval I ⊆ R. Assume that the image of C under f is contained in
I : f (C ) ⊆ I . Then the composition of g with f defined by

h(x) := g (f (x)),

is a convex function over C .

Proof.

Chapter 2: Convex analysis (Part 2) 21 / 28

 Convex functions Operations Preserving Convexity

Example 2.45:
2
The function h(x) = e ∥x∥ is a convex function over Rn since it can
be represented as h(x) = g (f (x)), where g (t) = e t is a nondecreasing
convex function and f (x) = ∥x∥2 is a convex function.
The function h(x) = (∥x∥2 + 1)2 is a convex function over Rn since it
can be represented as h(x) = g (f (x)), where g (t) = t 2 and
f (x) = ∥x∥2 + 1.

Chapter 2: Convex analysis (Part 2) 22 / 28

 Convex functions Operations Preserving Convexity

Example 2.45:
2
The function h(x) = e ∥x∥ is a convex function over Rn since it can
be represented as h(x) = g (f (x)), where g (t) = e t is a nondecreasing
convex function and f (x) = ∥x∥2 is a convex function.
The function h(x) = (∥x∥2 + 1)2 is a convex function over Rn since it
can be represented as h(x) = g (f (x)), where g (t) = t 2 and
f (x) = ∥x∥2 + 1.

Chapter 2: Convex analysis (Part 2) 22 / 28

 Convex functions Operations Preserving Convexity

Example 2.45:
2
The function h(x) = e ∥x∥ is a convex function over Rn since it can
be represented as h(x) = g (f (x)), where g (t) = e t is a nondecreasing
convex function and f (x) = ∥x∥2 is a convex function.
The function h(x) = (∥x∥2 + 1)2 is a convex function over Rn since it
can be represented as h(x) = g (f (x)), where g (t) = t 2 and
f (x) = ∥x∥2 + 1.

Chapter 2: Convex analysis (Part 2) 22 / 28

 Convex functions Operations Preserving Convexity

Another important operation that preserves convexity is the pointwise

maximum of convex functions.
Theorem 2.46:
Let f1 , . . . , fp : C → R be p convex functions over the convex set C ⊆ Rn .
Then the maximum function

f (x) := max fi (x)

i=1,...,p

is a convex function over C .

Chapter 2: Convex analysis (Part 2) 23 / 28

 Convex functions Operations Preserving Convexity

Example 2.47:
(i) f (x) = max{x1 , . . . , xn } is convex.
(ii) Given a vector x = (x1 , . . . , xn )T . Let x [i] denote the ith largest
value in x. For example,

x [1] = max{x1 , . . . , xn }

and
x [n] = min{x1 , . . . , xn }.
The function h(x) = x [1] is convex. However, in general the function
h(x) = x [i] is not convex. On the other hand, the sum of the k
largest components

hk (x) = x [1] + · · · + x [k] ,

is convex.

Chapter 2: Convex analysis (Part 2) 24 / 28

 Convex functions Operations Preserving Convexity

Example 2.47:
(i) f (x) = max{x1 , . . . , xn } is convex.
(ii) Given a vector x = (x1 , . . . , xn )T . Let x [i] denote the ith largest
value in x. For example,

x [1] = max{x1 , . . . , xn }

and
x [n] = min{x1 , . . . , xn }.
The function h(x) = x [1] is convex. However, in general the function
h(x) = x [i] is not convex. On the other hand, the sum of the k
largest components

hk (x) = x [1] + · · · + x [k] ,

is convex.

Chapter 2: Convex analysis (Part 2) 24 / 28

 Convex functions Operations Preserving Convexity

Example 2.47:
(i) f (x) = max{x1 , . . . , xn } is convex.
(ii) Given a vector x = (x1 , . . . , xn )T . Let x [i] denote the ith largest
value in x. For example,

x [1] = max{x1 , . . . , xn }

and
x [n] = min{x1 , . . . , xn }.
The function h(x) = x [1] is convex. However, in general the function
h(x) = x [i] is not convex. On the other hand, the sum of the k
largest components

hk (x) = x [1] + · · · + x [k] ,

is convex.

Chapter 2: Convex analysis (Part 2) 24 / 28

 Convex functions Operations Preserving Convexity

Example 2.47:
(i) f (x) = max{x1 , . . . , xn } is convex.
(ii) Given a vector x = (x1 , . . . , xn )T . Let x [i] denote the ith largest
value in x. For example,

x [1] = max{x1 , . . . , xn }

and
x [n] = min{x1 , . . . , xn }.
The function h(x) = x [1] is convex. However, in general the function
h(x) = x [i] is not convex. On the other hand, the sum of the k
largest components

hk (x) = x [1] + · · · + x [k] ,

is convex.

Chapter 2: Convex analysis (Part 2) 24 / 28

 Convex functions Operations Preserving Convexity

Example 2.47:
(i) f (x) = max{x1 , . . . , xn } is convex.
(ii) Given a vector x = (x1 , . . . , xn )T . Let x [i] denote the ith largest
value in x. For example,

x [1] = max{x1 , . . . , xn }

and
x [n] = min{x1 , . . . , xn }.
The function h(x) = x [1] is convex. However, in general the function
h(x) = x [i] is not convex. On the other hand, the sum of the k
largest components

hk (x) = x [1] + · · · + x [k] ,

is convex.

Chapter 2: Convex analysis (Part 2) 24 / 28

 Convex functions Operations Preserving Convexity

Example 2.47:
(i) f (x) = max{x1 , . . . , xn } is convex.
(ii) Given a vector x = (x1 , . . . , xn )T . Let x [i] denote the ith largest
value in x. For example,

x [1] = max{x1 , . . . , xn }

and
x [n] = min{x1 , . . . , xn }.
The function h(x) = x [1] is convex. However, in general the function
h(x) = x [i] is not convex. On the other hand, the sum of the k
largest components

hk (x) = x [1] + · · · + x [k] ,

is convex.

Chapter 2: Convex analysis (Part 2) 24 / 28

 Convex functions Operations Preserving Convexity

Theorem 2.48:
Let f : C × D → R be a convex function defined over the set C × D where
C ⊆ Rm and D ⊆ Rn are convex sets. Let

g (x) = min f (x, y ) ∀x ∈ C ,

y ∈D

where we assume that the minimum in the above definition is finite. Then
g is convex over C .

Proof.

Example 2.49: Let C ⊆ Rn be a convex set. The distance function

defined by
d(x, C ) = min{∥x − y ∥ : y ∈ C }
is convex.

Chapter 2: Convex analysis (Part 2) 25 / 28

 Convex functions Operations Preserving Convexity

Level sets

Definition 2.50:
Let f : C → R be a convex function over the convex set C ⊆ Rn and
α ∈ R. Then the level set of f with level α is given by

Lα f = {x ∈ C | f (x) ≤ α}.

A fundamental property of convex functions is that their level sets are

necessarily convex.

Chapter 2: Convex analysis (Part 2) 26 / 28

 Convex functions Continuity and Differentiability of Convex Functions

Local Lipschitz continuity of convex functions

Theorem 2.51:
Let f : C → R be a convex function over the convex set C ⊆ Rn . Let
x0 ∈ int(C ). Then there exist ϵ > 0 and L > 0 such that B(x0 , ϵ) ⊆ C and

|f (x) − f (x0 )| ≤ L∥x − x0 ∥

for all x ∈ B(x0 , ϵ).

Proof.

Chapter 2: Convex analysis (Part 2) 27 / 28

 Convex functions Continuity and Differentiability of Convex Functions

Existence of directional derivatives for convex function

Theorem 2.52:
Let f : C → R be a convex function over the convex set C ⊆ Rn . Let
x ∈ int(C ). Then for any d ̸= 0, the directional derivative f ′ (x; d) exists.

Chapter 2: Convex analysis (Part 2) 28 / 28