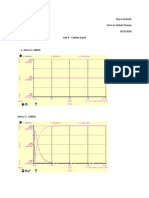
Solution:

Maximum velocity allowed for the rim before which the Batman has to reach to the
Flash = 650 m/s

distance between the Batman and the Flash (X) = 200 m

as both the Batman and the Flash start from rest,

The initial velocity of the Batman (UB) = 0

The initial velocity of the Flash (UF) = 0

Calculations for the Batman:

from V-t graph

Acceleration of the batman (aB) = slope of the graph = 50-0/ 10-0 = 5 m/s2

now time taken by the Batman to cover the distance of 200 m can be calculated by
using third equation of motion:

X = UB * tB + (1/2) * aB * tB2 ( Given UB = 0 )

200*2 = 5 * tB2

tB = ( 400/5)^ 1/2

tB = 8.94 s.

Calculations for the Flash:

We know that area under the acceleration time (a-t) graph gives the change in
velocity (ΔV = area under a-t curve )

therefore total change in velocity for the Flash:

ΔV = 5*50 + 5*100 = 750 m/s2

which is greater than the allowable velocity of 650 m/s2

therefore by putting ΔV = 650 m/s, as the maximum allowable change in velocity, we

can find out the time required to achieve this change,

now,

ΔV = ΔV1 + ΔV2 ( area under a-t graph in the first half + area under a-t graph in
the second half )

for the first half of a-t graph -

ΔVF1 = tF1*aF1

ΔVF1 = 5*50 = 250 m/s

so we know that maximum change will occur in the second half of the a-t graph,
therefore

for the second half-

ΔVF2 = tF2* aF2

ΔVF2 = tF2* 100....(2)

now,

combining 1 and 2 and putting ΔVF = 650 m/s

650 = 250 + tF2* 100

tF2 = 4 s.

Hence total time taken by the Flash to reach ΔV = 650 m/s is

tF = tF1 + tF2

tF = 5 (in the first half) + 4 (in the second half)

tF = 9 s.

as

tB ( 8.94) < tF ( 9 )

therefore the Batman reaches the flash before he attains the maximum allowable
change in his velocity and he will be able to stop the Flash.