Professional Documents
Culture Documents
Lebesgue Dominated Convergence Theorem and Generalized Form
Lebesgue Dominated Convergence Theorem and Generalized Form
Uploaded by
M Shahbaz0 ratings0% found this document useful (0 votes)
15 views4 pagesOriginal Title
Lebesgue dominated convergence theorem and generalized form
Copyright
© © All Rights Reserved
Available Formats
PDF or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
0 ratings0% found this document useful (0 votes)
15 views4 pagesLebesgue Dominated Convergence Theorem and Generalized Form
Lebesgue Dominated Convergence Theorem and Generalized Form
Uploaded by
M ShahbazCopyright:
© All Rights Reserved
Available Formats
Download as PDF or read online from Scribd
You are on page 1of 4
Vheorem 4.6 (Lebesgue Dominated Convergence Theorem)
Le e DoT
ne be integrable on E and {/,} be sequence of measurable
functions such that | f,|<2 on B. Suppose that lim f,(x) = f(x) 4.e, on
fi pp .e.
firms = fr lim fh
#. Then
Proof:
i oe iim IL) Sg 80 tims, = | S| g—fae on E.
Hence by Fatou’s lemma, we get
fires tim (ff +8) and fe-ss um (fe-%
Now fires tim (fats) = Jim (f+ fs) (By 4.4 Gi)
= um f+ fe
it fesim fae fe
Since fe < 2 s0 that {sim lim i oe)
sie forte fr sam fesy-tm frp
fo fi + im, appa Tm ep),
So fem fe see (MD,
Combining (+) and (**) we obtain
fein fos fas fe
Hence fre fe
Theorem 4.10 (Generalized Lebesgue Dominated Convergence Theorem)
Let {G,} be a sequence of integrable functions which
converges a.e. on E to an integrable funciton g. Let (F,} be a
sequence of measurable functions such that |F,| < G, and (F,)
converges tofa.e. on E.If fg = lim {em then f- lim i
Proof:
Since |F,| < G, and each G, is integrable-therefore each F,,
is integrable. Also lim |F,| = |lim F,| = [/] Slim G, = g and g is
integrable so f is integrable. From -G, < F, <'G, we have that
{F,+G,) and {G,-F,) are the sequences of non-negative measurable
functions and
F, +G,>/+gae.onBandG,-F,>g-fae. on E,
‘Thus by Fatou’s lemma, we obtain
ir £5 lim (fF, + G,) and fe-f5 lim ([6,-F,)
jm B+ fe
capter 4 Lebésgue Integration 183
orther i “fe fe psa (fe.-¥,)
im fe, ~ Tm fr, = fe oe
Thus Pe Tim fe
Form (*) and (**) we get the required result.
proposition 4.11
‘Suppose that fis an arbitrary measurable function on E. If
jedae. on E, So then f- 0.
Proof:
Iff = Oae. on E, then either, ff? and f are zero a.e. on E or
f =f ae. on Bin both the cases we get fr- .
.
‘The converse of the above proposition is false as follows:
Example 4.12
+1 forx20
Define f:(-1, > (1-1 bY" 1a forx <0
Clearly fis a measurable function.
tele ir “+120
However the function fis not zero 0. on E
Corollary 4.13
= (41
‘Suppose f is a measurable function on E. If A & E with
n(A)=0, then {f= 0,
a
You might also like
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5813)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (844)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (822)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (348)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1092)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Fato's Lemma and Monotone Convergence TheoremDocument5 pagesFato's Lemma and Monotone Convergence TheoremM ShahbazNo ratings yet
- 5405Document230 pages5405M ShahbazNo ratings yet
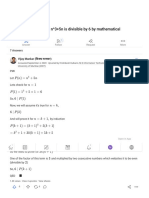
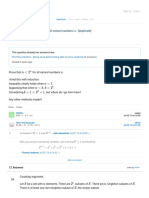
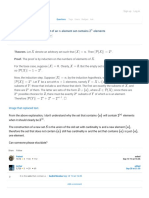
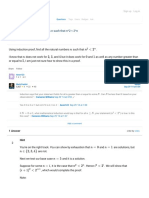
- Prove That Is Divisible by 6 For All (Duplicate) : Mathematics Sign Up Log inDocument4 pagesProve That Is Divisible by 6 For All (Duplicate) : Mathematics Sign Up Log inM ShahbazNo ratings yet
- ConductionOfHeatInSolids 1Document2 pagesConductionOfHeatInSolids 1M ShahbazNo ratings yet
- SAG 2017: Finite Groups: Austin Alderete Jun. 2nd, 2017Document6 pagesSAG 2017: Finite Groups: Austin Alderete Jun. 2nd, 2017M ShahbazNo ratings yet
- HW1 SolutionDocument2 pagesHW1 SolutionM ShahbazNo ratings yet
- Question 6iDocument7 pagesQuestion 6iM ShahbazNo ratings yet
- For David Prove That 5 N - 4n - 1 Is Divisible by 16 For All : Math HomeworkDocument8 pagesFor David Prove That 5 N - 4n - 1 Is Divisible by 16 For All : Math HomeworkM ShahbazNo ratings yet
- Search For Questions & ChaptersDocument4 pagesSearch For Questions & ChaptersM ShahbazNo ratings yet
- For David Prove That 5 N - 4n - 1 Is Divisible by 16 For All : Math HomeworkDocument8 pagesFor David Prove That 5 N - 4n - 1 Is Divisible by 16 For All : Math HomeworkM ShahbazNo ratings yet
- Question 9Document4 pagesQuestion 9M ShahbazNo ratings yet
- N 2 N N 1 N KK 2 K + 1 : Prove That For All Natural Numbers - (Duplicate)Document6 pagesN 2 N N 1 N KK 2 K + 1 : Prove That For All Natural Numbers - (Duplicate)M ShahbazNo ratings yet
- Prove by Induction That (Duplicate)Document3 pagesProve by Induction That (Duplicate)M ShahbazNo ratings yet
- Prove That, For All by Mathematical InductionDocument3 pagesProve That, For All by Mathematical InductionM ShahbazNo ratings yet
- X - N - P (X) - 2: Prove That The Power Set of An - Element Set Contains ElementsDocument5 pagesX - N - P (X) - 2: Prove That The Power Set of An - Element Set Contains ElementsM ShahbazNo ratings yet
- PF 20Document1 pagePF 20M ShahbazNo ratings yet
- Find All Natural Numbers N Such That N 2 2 N: Mathematics Sign Up Log inDocument3 pagesFind All Natural Numbers N Such That N 2 2 N: Mathematics Sign Up Log inM ShahbazNo ratings yet
- Homework6 Solution IanDocument3 pagesHomework6 Solution IanM ShahbazNo ratings yet
- Solutions To Homework 2-MAT319/320: 1 Section 1.3Document3 pagesSolutions To Homework 2-MAT319/320: 1 Section 1.3M ShahbazNo ratings yet