CHAPTER: 12 LINEAR PROGRAMMING CLASS XII

PROBLEMS
DELETED 2020-21
Mathematical formulation of L.P. problems=> NO WORD PROBLEMS
& Unbounded graphical solutions.

Objective function Linear function Z = ax + by, where a, b are constants, which has
to be maximised or minimized is called a linear objective function.

Constraints The linear inequalities or equations or restrictions on the variables of a

linear programming problem are called constraints. The conditions x ≥ 0, y ≥ 0 are
called non-negative restrictions.

Optimisation problem A problem which seeks to maximise or minimise a linear

function (say of two variables x and y) subject to certain constraints as determined
by a set of linear inequalities is called an optimisation problem. Linear
programming problems are special type of optimisation problems.
Feasible region The common region determined by all the constraints including
non-negative constraints x, y ≥ 0 of a linear programming problem is called the
feasible region (or solution region) for the problem. The region other than feasible
region is called an infeasible region.
Optimal (feasible) solution: Any point in the feasible region that gives the optimal
value (maximum or minimum) of the objective function is called an optimal solution.

Theorem 1 Let R be the feasible region (convex polygon) for a linear programming
problem and let Z = ax + by be the objective function. When Z has an optimal value
(maximum or minimum), where the variables x and y are subject to constraints
described by linear inequalities, this optimal value must occur at a corner point*
(vertex) of the feasible region.
Theorem 2 Let R be the feasible region for a linear programming problem, and let
Z = ax + by be the objective function. If R is bounded, then the objective function
Z has both a maximum and a minimum value on R and each of these occurs at a
corner point (vertex) of R.

SMITA DEY KV ONGC PANVEL Page 1 of 16

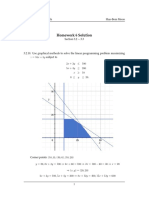
Example: Solve the following problem graphically:
This is objective → Minimise and Maximise Z = 3x + 9y ... (i)
subject to the constraints: x + 3y ≤ 60 ... (ii)
These are → x + y ≥ 10 ... (iii)
x ≤ y ... (iv)
constraints →
x ≥ 0, y ≥ 0
First Step: X + 3y = 60 x + y = 10 x=y
X 0 X 0 x 0
Draw the
y 0 y 0 y 0
inequalities
Eqn (ii)(iii)(iv)
(i.e constraints)
the way it was
done in class XI

Second Step:
Identify all corner Corner points Z = 3x + 9y
points (vertex) of A(0,10) 90
feasible region B(5,5) 60  min
and make a table C(15,15) 180 max
as shown→ D(0,20) 180 max
Conclusion Z min = 60 at (5,5) &
Since Z max at C(15,15) & D(0,20)
 Zmax = 180 at all points on line
segment CD

SMITA DEY KV ONGC PANVEL Page 2 of 16

 EXERCISE 12.1

1 Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
2 Minimise Z = – 3x + 4 y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
3 Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
4 Minimise Z = 3x + 5y
such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0. X unbounded
5 Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
6 Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0. X unbounded
7 Minimise and Maximise Z = 5x + 10 y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
8 Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
9 Maximise Z = – x + 2y, subject to the constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0. X unbounded
10 Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
No feasible region

SMITA DEY KV ONGC PANVEL Page 3 of 16

EXTRA QUESTIONS

1 Maximize and Minimize Z = 5x + 2y

Subject to constraints: x – 2y ≤ 2
3x + 2y ≤ 12 , -3x + 2y ≤ 3, x,y ≥0
Ans: Zmin = 3 at (0,3/2)
Zmax = 19 at (x,y)=(7/2,3/4)

SMITA DEY KV ONGC PANVEL Page 4 of 16

2 Maximize and Minimize Z = 3x + 2y
Subject to constraints: x + y ≤ 100
x + y ≥ 60 , x ≤ 60, y ≤ 50
Ans: Zmin = 130 at (10,50)
Zmax = 260 at (x,y)=(60, 40)

3 Maximize and Minimize Z = 4x + 3y

Subject to constraints: x + y ≤ 200
x ≥ 20 , x ≤ y, x,y≥0

4 Maximize and Minimize Z = 5x + 10y

Subject to constraints: x + 2y ≤ 120
x + y ≥ 60 , x - 2y ≥ 0, x,y ≥ 0
Ans: Zmin = 300 at (60,0)
Zmax = 600 at line segment joining (120,0) & (60,30)

SMITA DEY KV ONGC PANVEL Page 5 of 16

5 Maximize and Minimize Z = x + 2y
Subject to constraints: x + 2y ≥ 100
2x + 5y ≤ 100 , 2x + y ≤ 200, x,y ≥ 0
Ans: Zmin = 100 at line segment joining (20,40) & (0,50)
Zmax = 400 at (0,200)

6 Maximize Z = x + y
Subject to constraints:
8x + 5y ≤ 200 , 2x + 5y ≤ 100, x,y ≥ 0
Ans: Zmax = 30 at (50/3, 40/3)  don’t convert to decimal
or approx… keep it as it is for calculation purpose.

SMITA DEY KV ONGC PANVEL Page 6 of 16

SMITA DEY KV ONGC PANVEL Page 7 of 16
SMITA DEY KV ONGC PANVEL Page 8 of 16
SMITA DEY KV ONGC PANVEL Page 9 of 16
7 Solve the following linear programming problem (L.P.P)
graphically.
Maximize 𝑍=𝑥+2𝑦
subject to constraints ;
𝑥+2𝑦 ≥ 100, 2𝑥−𝑦 ≤ 0, 2𝑥+𝑦 ≤ 200, 𝑥,𝑦≥0
[CBSE SAMPLE PAPER 2020-21]

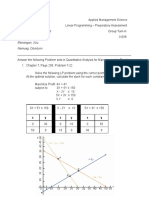
8)
The corner points of
the feasible region
determined by the
system of linear
constraints are as
shown →

Answer each of the

following:

(i) Let 𝑍=3𝑥−4𝑦 be the objective function. Find the maximum

and minimum value of Z and also the corresponding points at
which the maximum and minimum value occurs.

(ii) Let 𝑍=𝑝𝑥+𝑞𝑦,where 𝑝,𝑞>𝑜 be the objective function. Find the

condition on 𝑝 and 𝑞 so that the maximum value of 𝑍 occurs at
B(4,10)𝑎𝑛𝑑 C(6,8). Also mention the number of optimal
solutions in this case.

SMITA DEY KV ONGC PANVEL Page 10 of 16

SMITA DEY KV ONGC PANVEL Page 11 of 16
SMITA DEY KV ONGC PANVEL Page 12 of 16
SMITA DEY KV ONGC PANVEL Page 13 of 16
SMITA DEY KV ONGC PANVEL Page 14 of 16
SMITA DEY KV ONGC PANVEL Page 15 of 16
SMITA DEY KV ONGC PANVEL Page 16 of 16