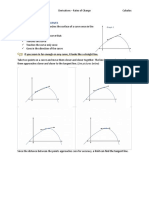
Differential Calculus: Introduction and Let's say you take a ride from Farmers

Definition of Derivatives Cubao going to SM Val. You travel 15

kilometers in 3 hours. What would your
● Differential Calculus – it is a branch average speed be?
of calculus that studies the rates at
which quantities change.
● Differentiate – to find the derivative
of the function.
● Differentiation – the process of
getting the derivatives.
● Derivative – the rate of change of a
function with respect to a variable. Let us relate to Physics in getting the rate of
change. As we can see on the graph, it
Secant Line- A secant line is a started from rest (original position) to its
linear approximation of a function between 2 destination (final position).
points. A secant line, also simply called a
secant, is a line passing through two points The slope of the red line represents the
of a curve. As the two points are brought average rate of change or in this case
together (or, more precisely, as one is average speed.
brought towards the other), the secant line
tends to a tangent line.

Tangent Line- A tangent line to a curve is a

The slope of a secant line represents the
average of the function between two
points (rate of change).
What does it mean by average speed or
average rate of change? It means change of
position (or displacement) with respect to
time over an interval (or in this case
between 2 points)
line that just touches a curve at a given
point. A linear approximation to the curve
at a given point. It represents the
instantaneous rate of change of the
function at a given point. The tangent line
(or simply tangent) to a plane curve at a
given point is the straight line that "just
touches" the curve at that point. Leibniz
defined it as the line through a pair of
infinitely close points on the curve.
What does it mean by instantaneous rate of
change? It is the specific rate of change of
position (or displacement) with respect to
time at a single point.

How can we find the slope of a tangent line

if we only know one point on the line?

Since we are dealing with a secant line, we can easily

find its slope if 2 points are given on the curve. But
how can we find the slope of the tangent line if we
only know one point?
Definition of DERIVATIVES
Start by getting the slope of a secant line by taking
two points.

Commonly Used Notations of Derivatives

From the secant line slope formula, we can also derive the slope of the
tangent line. However, since it’s a tangent line, it only touches the curve at
one point, and to get the slope we need to use 2 points. In this particular
example, we will use the concept of limits. We make delta x become smaller
and smaller as we approach the point of tangency. So papaliitin natin yun
value nya para uusod yung ng secant line until makuha natin yung one point
lang that touches the curve which is the tangent line.
HOW TO FIND THE DERIVATIVE

EXAMPLE: