Assignment-I

MTH-201, MTH-201A
Linear Algebra
Due Tuesday May 27th at 5:00 p.m

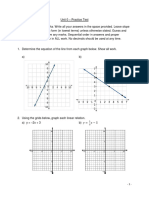
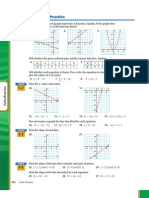
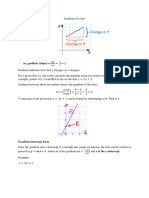
1. Find all solutions to the following linear system of equations by Gauss-Jordan elmi-
nation method (row reduced echelon form):

3x + 2y − z − 2w = 5
4x + 3y − 2z + 2w = 3
−2x − y + 6w = −7

2. Find the inverse of the following matrix using row reduced echelon form:
 
3 4 −1
A =  1 −1 1 
−1 2 3

(Hints: Write the row reduced echelon form of the matrix (A|I). If A reduces to I, then
(A|I) reduces to (I|A−1 ).
3. Show that the vectors u = (1 + i, 2i), v = (1, 1 + i) ∈ C2 are linearly dependent over
C, but linearly independent over R.
4. Find 3 vectors u, v and w in R4 such that {u, v, w} is linearly dependent whereas
{u, v}, {u, w}, and {v, w} are linearly independent. Extend each of the linearly independent
sets to a basis of R4 .
5. Let W1 = {(x, y, z) : x = y = z} and W2 = {(x, y, z) : x = 0}. Prove that
(i) W1 and W2 are subspaces of R3 .
(ii) R3 = W1 ⊕ W2 .
6. Let V and W are finite dimensional vector spaces over a field F and let L(V, W )
denote the set of all linear tranformations from V to W . Prove that
(i) L(V, W ) is a vector space over F .
(ii) Find an explicit basis for L(V, W ) and conclude that dim(L(V, W )) = dim(V ).dim(W ).