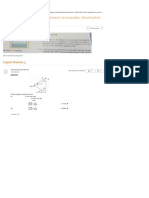
Ke haha has Figure 14-50. Kealized layered sytem. “The basic idca used in Stiles’ method and the Dykstra_Parsons method is to determine the frontal position in each layer at the time water breakthrough ‘occurs in successive layers. Ifthe flow capacity of each layer is defined by the product of permeability and thickness, i. kh, then the water and oil flow rates from all layers can be calculated to yield the producing water-oil ratio. Stiles’ Method ‘Stiles (1949) proposed an approach that takes into account the effect of permeability variations in predicting the performance of waterfloods. Siiles assumes that in a layered systcm, the water breakthrough occurs in ‘a sequence that starts in the layer with the highest permeability. Assum- ing that the reservoir is divided into n layers that are arranged in a descending permeability order with breakthrough occurring in a layer i, all layers from 1 to i have already been swept by water. The remaining layers obviously have not reached breakthrough. “The method assumes that there is piston-like displacement of oil, so that after water breakthrough in a layer, onfy water is produced from this layer. After water breakthrough, the producing WOR is given by:‘where C is the faction of the total flow capacity represented by layers that have water breakthrough. Based on the above concept. Stiles proposed that the vertical sweep cfficiency can be calculated from the following expression: aoe (14-90) where i =breakthrough layer, ie i= 1,23,-.-m If the values of the porosity vary between layers, Fquation 14.90 can be vwiten: “a A ©) ¥(¢0),+ ¥ (an), Gee ‘Stiles also developed the following expression for determining the sur face water-ol ratio as breakthrough occurs in any layer: De, wor, =a) (14-92) (14-93)1052 Reservoir Engineering Hanabook where WOR, = surface water-oil ratio, STR/STR. Ke =relative permesbility to water af Sue ky =relative permeability o oil at Sut Both the vertical swexp efficiency and surface WOR equations arc used multancously to describe the sequential breakthrough as it occurs in yyer I through layer n. It is usually convenient to represent the results of those calcalations graphically in terms of log(WOR,) as a function of Fy. Example 14-21 ‘The Dykstra and Parsons (1950) permeability ordering approach is used to describe a reservoir by the following five-layer system: layer md 1 nS ‘ ss 0 5 30 0 ‘The reservoir is under consideration for further development by water injection. 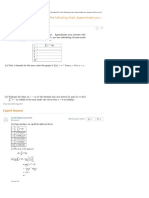The fellowing additional information is available: Calculate the vertical sweep efficiency and surface water-oil ratio using Stiles’ method: Solution Step 1. Calculate parameter A using Equation 14-93: 03 (2.0¥120) ogy 09 (05x00)Prncipes of waterfooding 1033 Step 2. Caleul layer, i =1, by applying Equations 14-90 and 14-92: «Yn, Dk), r 4 [hha eghy +h + phy Kh _{12005) + 0015) + (7000) + (55}10) + (30}10)]_ 5 55 ~ (120\0) - Yom, wor, =(1584) 2 — Sem, Ey and WOR, when breakthrough occurs in the first (in), (ea), + (am), + (en), + (eR), (x oyEsy + HaK 10} + 58KF0) + GOTO) 0.983 STH/STS Step 3. Calculate Ey and WOR, when water breakthrough occurs in the second layer, ic, = 2: WOR, =(1.584) WOR, =(1.584) + Sn), te Ey i seg = Kalba ths) +[ (en), +(e, +(e, Eh, _ 90415-+15) +[(70K10) +(55\(10) + (30)(10)] _ ~~ (9060) 07871054 Reservoir Engineering Handbook 2 Deen), WOR, =(1.584)- 51 —_ Yen), Ss i (kh), + (kh) WOR OST), HO, (120)(15)+(90\(15) (7010) + (5510) + (3010) Step 4. The required calculations can be performed! 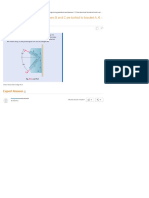more conveniently in the following worksheet WOR, = (1.584) =3.22 STB/STB nae 6 © @ @ layer beh Dh katy eh Soh hha 1 120 15 15 1.800 1,800 1900 7200 0Ks3 0983 2 9 15 30 2700 1350 3150 5400 O77 32 3 7 10 40 2800 700 3850 4200 © 0.86 au 4°55 1 50 2750 550 4400 3300 © ost a2 5 W 10 6 10 30 4700 1800 1.000 =e sum = 4700 Figure 14-51 shows the resulting relationship between the vertical sweep efficiency and producing WOR. The curve can be extended to WOR = 0 to give the vertical sweep efficiency at breakthrough Ev. ‘The Dykstra—Parsons Method Dykstra and Parsons (1950) correlated the vertical sweep efficiency with the following parameters: + Permeability variation V ‘+ Mobility ratio M ‘+ Watcr-oil ratio WOR, as expressed in bbY/bbL ‘The authors presented their correlation in 2 graphical form for water-oil ratios of 0.1, 0.2, 0.5, 1, 2, 5, 10, 25, 50, and 100 BbUbbI. Figure 14.52 shows Dykstra and Parsons’ graphical correlation for a WOR of 50 bbWMbl. Using a regression analysis model, deSouza and Brigham