Sommerfeld’s relativistic atom model:

To explain the observed fine structure of spectral lines, Sommerfeld introduced

two main modification in Bohr’s theory.
(1) According to Sommerfeld, the path of an electron around the nucleus, in
general, is elliptic i.e., an electron revolve round the nucleus in elliptic orbits with
the nucleus at one of the foci. The circular orbits are a special case.
(2) The velocity of electron moving in an elliptic orbit varies considerably at
different parts of the orbit. This causes relativistic variation in the mass of the
𝑚0
moving electron {v=2.2x106 ms-1, 𝑚 = 2
}. Therefore he took into account
√1−𝑣2
𝑐
the relativistic variation of the mass of the electron with velocity. Hence this
model is also called as relativistic atom model.
Theory:
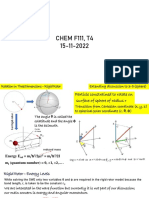
Consider the electron moving in an elliptic orbit around
the nucleus. Its position at any instant is described in
terms of polar coordinates r and φ as shown in figure.
Since r and φ both varies in an elliptical orbit, the
electron is endowed with two momentums with
changing r and φ i.e., radial momentum Pr and azimuthal
or orbital momentum Pφ. According to Bohr’s theory, these two momenta should
be quantised. The two quantisation condition are
∫ 𝑃𝑟 𝑑𝑟 = nr h ......... (1) and ∫ 𝑃𝜑 𝑑𝜑 = nφ h ......... (2)
Where nr is called the radial quantum number and nφ is called the angular or
azimuthal quantum number. nr and nφ take only positive integral values such that
nr + nφ = n, where n is the principal quantum number which takes the integral
values 1,2,3 ........∞.
Determination of allowed elliptical orbits:
The allowed elliptical orbits of an electron are determined by evaluating integrals
in equation (1) and (2).
Consider the integral in equation (2). The momentum 𝑃𝜑 corresponds to the
coordinate φ is merely the angular momentum P of the electron in elliptic orbit
which is constant, from Kepler’s law i.e., Pφ = P = constant. Integrating equation
(2) from 0 to 2π
2π 2π
∫0 𝑃𝜑 𝑑𝜑 = nφ h or 𝑃𝜑 ∫0 𝑑𝜑 = nφ h or
𝒏𝝋 𝒉
𝑷𝝋 = ........ (3)
𝟐𝝅
 1 𝜖 𝑐𝑜𝑠𝜑
Consider the equation of ellipse in polar form = and substituting
𝑟 𝑎(1−𝜖 2 )
this in equation (1) and simplifying further we get the condition for allowed
elliptic orbits
𝑛∅2 𝑏2
1– ε =
2
2
, for an ellipse 1– ε2 = where a and b are semi-major and semi-
𝑛 𝑎2
minor axes respectively.

𝑏2 𝑛∅2 𝒃 𝒏∅
Hence
𝑎2
= 𝑛2 or = ........ (4)
𝒂 𝒏
Equation (4) is the condition that determines the allowed elliptical orbits. The
allowed elliptical orbits are those for which the ratio of semi-major and minor
axes is that of two integers. When
a) nφ = n implies b = a and the orbit becomes circular
b) nφ ≠ 0, since the ellipse would then degenerate into a straight line passing
through the nucleus.
c) nφ cannot be greater than n, since b is always than n.
Hence for a given value of n, nφ can take only n different values, which means
there can be only n elliptical orbits of different eccentricities.

For n=1, there is only one possible orbit which

is circular. For n=2, there are two possible
orbits, one circular and the other elliptic which
are designated as 21 and 22. For n=3, there are
3 possible orbits which are designated as 31, 32
and 33 and so on, the subscript being the
azimuthal quantum number nφ.
Fig. Permitted electron orbits