Professional Documents
Culture Documents
Slides MO Component8
Uploaded by
sreram20220 ratings0% found this document useful (0 votes)
2 views13 pagesOriginal Title
Slides_MO_Component8 (1)
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
2 views13 pagesSlides MO Component8
Uploaded by
sreram2022Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 13
Module MO-Component 8
Chapter 4-Section 4.1.1: Fitting procedure for the
Gamma process
Master course ‘Advanced Maintenance and Service Logistics’
Lecturer: Geert-Jan van Houtum
OVERVIEW
Chapter 4: Degradation models
Component 8 is about:
• Section 4.1.1: Fitting procedure for the Gamma process
1 /School of Industrial Engineering
4.1.1 Fitting procedure for the Gamma process
Given:
Samples of the degradation paths of m items (components),
n measurements per item
2 /School of Industrial Engineering
4.1.1 Fitting procedure for the Gamma process (cont.)
Notation:
• Item i, measurement j: time ti,j , degradation level xi,j
• Define:
• ti,0 :=0 and xi,0 :=0 for all i=1,…,m
• ∆ti,j = ti,j − ti,j-1 and ∆xi,j = xi,j − xi,j-1 for all i=1,…,m and j=1,…,n
• The ∆xi,j are samples for Gamma distributed variables (with
different shape parameters)
3 /School of Industrial Engineering
4.1.1 Fitting procedure for the Gamma process (cont.)
To be estimated: (alternative) parameters µ and σ
Special case: ∆ti,j = t for all i=1,…,m and j=1,…,n
Then:
• All ∆xi,j are samples of a Gamma distribution with mean µt and
variance σ2t
• Unbiased estimator for µt (by standard statistics):
1 𝑚𝑚 𝑛𝑛
� � ∆𝑥𝑥𝑖𝑖,𝑗𝑗
𝑚𝑚𝑚𝑚 𝑖𝑖=1 𝑗𝑗=1
4 /School of Industrial Engineering
4.1.1 Fitting procedure for the Gamma process (cont.)
Special case (cont.):
• Unbiased estimator for µ:
1 1 𝑚𝑚 𝑛𝑛
𝜇𝜇� = � � ∆𝑥𝑥𝑖𝑖,𝑗𝑗
𝑡𝑡 𝑚𝑚𝑚𝑚 𝑖𝑖=1 𝑗𝑗=1
• Unbiased estimator for σ 2t (notice: mean of ∆𝑥𝑥𝑖𝑖,𝑗𝑗 is 𝜇𝜇t): �
1 𝑚𝑚 𝑛𝑛 2
� � ∆𝑥𝑥𝑖𝑖,𝑗𝑗 − 𝜇𝜇𝑡𝑡
�
𝑚𝑚𝑚𝑚 𝑖𝑖=1 𝑗𝑗=1
• Unbiased estimator forσ 2:
2
1 1 𝑚𝑚 𝑛𝑛 2
𝜎𝜎� = � � ∆𝑥𝑥𝑖𝑖,𝑗𝑗 − 𝜇𝜇𝑡𝑡
�
𝑡𝑡 𝑚𝑚𝑚𝑚 𝑖𝑖=1 𝑗𝑗=1
5 /School of Industrial Engineering
4.1.1 Fitting procedure for the Gamma process (cont.)
The following theorem gives the estimators for µ and σ 2 for the
general case.
Theorem 4.1. Unbiased estimators for µ and σ2 are given by
∑𝑚𝑚 ∑ 𝑛𝑛
𝑖𝑖=1 𝑗𝑗=1 ∆𝑥𝑥𝑖𝑖𝑖𝑖
𝜇𝜇̂ = 𝑚𝑚 𝑛𝑛
∑𝑖𝑖=1 ∑𝑗𝑗=1 ∆𝑡𝑡𝑖𝑖𝑖𝑖
2
∑𝑚𝑚 ∑ 𝑛𝑛
∆𝑥𝑥𝑖𝑖𝑖𝑖 − 𝜇𝜇∆𝑡𝑡
𝑖𝑖=1 𝑗𝑗=1 ̂ 𝑖𝑖𝑖𝑖
𝜎𝜎� 2 =
1 2
∑𝑚𝑚 ∑ 𝑛𝑛
∆𝑡𝑡𝑖𝑖𝑖𝑖 − 𝑚𝑚 𝑛𝑛 ∑ 𝑚𝑚 ∑𝑛𝑛
∆𝑡𝑡
𝑖𝑖=1 𝑗𝑗=1 ∑𝑖𝑖=1 ∑𝑗𝑗=1 ∆𝑡𝑡𝑖𝑖𝑖𝑖 𝑖𝑖=1 𝑗𝑗=1 𝑖𝑖𝑖𝑖
6 /School of Industrial Engineering
Example 4.1
7 /School of Industrial Engineering
Example 4.1 (cont.)
8 /School of Industrial Engineering
Example 4.1 (cont.)
• ∆ti,j = 4 for all i=1,…,m and j=1,…,n. Hence simplified formulas
applicable.
• We find the following unbiased estimator for µ (in 10-5 m):
1 1
𝜇𝜇̂ = ∑𝑚𝑚 ∑ 𝑛𝑛
𝑖𝑖=1 𝑗𝑗=1 ∆𝑥𝑥𝑖𝑖,𝑗𝑗
𝑡𝑡 𝑚𝑚𝑚𝑚
1 1
= ∑6𝑖𝑖=1 𝑥𝑥𝑖𝑖,11
4 6×11
1
= 311 + 417 + 300 + 444 + 530 + 403 = 9.1098
264
9 /School of Industrial Engineering
Example 4.1 (cont.)
• We find the following unbiased estimates for µ and σ2:
1 1 2
𝜎𝜎� 2 = ∑𝑚𝑚 ∑𝑛𝑛
𝑖𝑖=1 𝑗𝑗=1 ∆𝑥𝑥𝑖𝑖,𝑗𝑗 − 𝜇𝜇𝑡𝑡
�
𝑡𝑡 𝑚𝑚𝑚𝑚
1 1 6 11 2
= � � ∆𝑥𝑥𝑖𝑖,𝑗𝑗 − 9.1098×4 = … (Excell) … = 234.7164
4 6×11 𝑖𝑖=1 𝑗𝑗=1
• Next, we can compute unbiased estimators for the corresponding
α and β:
𝜇𝜇�2 (9.1098)2 𝜇𝜇� 9.1098
𝛼𝛼� = 2 = ̂
= 0.3536, 𝛽𝛽 = 2 = = 0.0388
𝜎𝜎� 234.7164 𝜎𝜎� 234.7164
10 /School of Industrial Engineering
Example 4.1 (cont.)
Sample paths of
fitted Gamma process:
11 /School of Industrial Engineering
TAKEOUT
Chapter 4: Degradation models
Component 8 is about:
• Section 4.1.1: Fitting procedure for the Gamma process
You are expected to be able to calculate estimators for the parameters of
a Gamma process
12 /School of Industrial Engineering
You might also like
- MScFE 610 ECON - Compiled - Notes - M3Document26 pagesMScFE 610 ECON - Compiled - Notes - M3sadiqpmpNo ratings yet
- Techniques of IntegrationDocument50 pagesTechniques of Integrationhey hey100% (1)
- Lecture 8 BackpropagationDocument28 pagesLecture 8 BackpropagationHodatama Karanna OneNo ratings yet
- WQU Econometrics M3 Compiled Content PDFDocument44 pagesWQU Econometrics M3 Compiled Content PDFNarayani PandeyNo ratings yet
- MOW323 - Semester Test 1Document10 pagesMOW323 - Semester Test 1Nicholas RuestNo ratings yet
- Instruction: Technique Indicated in The Question Will Receive No PointDocument7 pagesInstruction: Technique Indicated in The Question Will Receive No Pointชาเย็น เย็นชาNo ratings yet
- Experiment 09Document6 pagesExperiment 09Usman AliNo ratings yet
- Problema 6-23 ShigleyDocument7 pagesProblema 6-23 ShigleylosdesquiciadosNo ratings yet
- Lecture 01 - Review of FundamentalsDocument6 pagesLecture 01 - Review of FundamentalsCaden LeeNo ratings yet
- Plackett BurmanDocument46 pagesPlackett BurmanalexNo ratings yet
- Experiment 08Document6 pagesExperiment 08Usman AliNo ratings yet
- Stat2 2023 Syllabus B v1.0 Weeks 5-6-7Document41 pagesStat2 2023 Syllabus B v1.0 Weeks 5-6-7Andrei PopaNo ratings yet
- Otto Cycle and Diesel Cycle - MEENG324Document15 pagesOtto Cycle and Diesel Cycle - MEENG324King Cyruz PabloNo ratings yet
- IntegralDocument4 pagesIntegralHarvey SantosNo ratings yet
- MEE 561 Lecture Notes - Free Damped VibrationsDocument17 pagesMEE 561 Lecture Notes - Free Damped VibrationsProspect Teaches MathematicsNo ratings yet
- MEE 411 Lecture Notes - Free Damped VibrationsDocument17 pagesMEE 411 Lecture Notes - Free Damped VibrationsProspect Teaches MathematicsNo ratings yet
- ModalAnalysis ExampleDocument4 pagesModalAnalysis ExampleAmeya BandekarNo ratings yet
- Sample Exam For Luminita Stevens Intermediate MacroeconomicsDocument5 pagesSample Exam For Luminita Stevens Intermediate MacroeconomicsKevin ShaughnessyNo ratings yet
- Data Collection and SummationDocument4 pagesData Collection and SummationJet jet GonzalesNo ratings yet
- 1piece Mathematics Pre Board 1 Solutions 110344Document24 pages1piece Mathematics Pre Board 1 Solutions 110344REMY CUBERONo ratings yet
- Assignment 10 AnsDocument10 pagesAssignment 10 AnsAnuska DeyNo ratings yet
- İTÜ FBE - UUM510E Computational Fluid Dynamics: 2020-2021 Spring Semester Project 3Document11 pagesİTÜ FBE - UUM510E Computational Fluid Dynamics: 2020-2021 Spring Semester Project 3Erkan ÜnNo ratings yet
- Kelompok 3 - Tugas 6 - TRK2-03-dikonversiDocument30 pagesKelompok 3 - Tugas 6 - TRK2-03-dikonversiMuhammad AzharNo ratings yet
- Memo Exam 2023 FinalDocument7 pagesMemo Exam 2023 Finalcawhite0804No ratings yet
- Final Exam-2018Document3 pagesFinal Exam-2018혁준No ratings yet
- Multiple IntegralsDocument5 pagesMultiple IntegralsMohammad Mehdi NorooziNo ratings yet
- Homework 4 SolutionDocument10 pagesHomework 4 SolutionKai SamaNo ratings yet
- Piping NetworksDocument14 pagesPiping NetworksKarel Grace ColotNo ratings yet
- 1.3 Runtime ExpressionsDocument15 pages1.3 Runtime ExpressionsStanley WangNo ratings yet
- ISE503 Project ReportDocument6 pagesISE503 Project ReportDidik HariadiNo ratings yet
- Dimensional Analysis Lecture 21 BatchDocument33 pagesDimensional Analysis Lecture 21 BatchRenuja LakviduNo ratings yet
- BMEN 383 - Lab 6Document10 pagesBMEN 383 - Lab 6Varun NairNo ratings yet
- DSGE Lecture 6 - FES - 00006Document77 pagesDSGE Lecture 6 - FES - 00006imkroslayNo ratings yet
- Bayesian ApproachDocument6 pagesBayesian ApproachJuan Camilo LópezNo ratings yet
- L-19 (P K Formula)Document11 pagesL-19 (P K Formula)Anisha GargNo ratings yet
- CHEG443 Week 9 C7 Lec 13 KDocument34 pagesCHEG443 Week 9 C7 Lec 13 KAnders Rojas Coa.No ratings yet
- The Power FormulaDocument17 pagesThe Power FormulaLyssa ChoiNo ratings yet
- FEE321 Lecture - 5 - Singularity Functions - 2hrsDocument57 pagesFEE321 Lecture - 5 - Singularity Functions - 2hrsPeter JumreNo ratings yet
- Lec 3 Num MeasuresDocument5 pagesLec 3 Num Measuresowronrawan74No ratings yet
- DSP Module 2Document37 pagesDSP Module 2keerti hattiNo ratings yet
- Ee221 Ch9 SolDocument4 pagesEe221 Ch9 SolHarish PallaNo ratings yet
- Solution Session 4 E1 E2 Runoff Hydrograph TransformationDocument11 pagesSolution Session 4 E1 E2 Runoff Hydrograph TransformationTiên PhạmNo ratings yet
- EG2101-L21a RT2014 PDFDocument23 pagesEG2101-L21a RT2014 PDFvilukNo ratings yet
- Exam With SolutionsDocument7 pagesExam With SolutionsCarlos Andres Pinzon LoaizaNo ratings yet
- Integration I Lecture08Document22 pagesIntegration I Lecture08paulkhor74No ratings yet
- Solution of Swing Equation: Home Work - 2. Euler Method: Home Work - 3. Modified Euler MethodDocument10 pagesSolution of Swing Equation: Home Work - 2. Euler Method: Home Work - 3. Modified Euler MethodK.R.Sampath kumarNo ratings yet
- S9-P5 Mrabti PaperDocument10 pagesS9-P5 Mrabti PaperGhita ZazNo ratings yet
- Assignment 1Document13 pagesAssignment 1Si Woo LeeNo ratings yet
- Please Show Your Work in Order To Receive Full CreditDocument4 pagesPlease Show Your Work in Order To Receive Full CreditMarian KhouryNo ratings yet
- Quiz 2 and SolDocument14 pagesQuiz 2 and SolMuhammad AslamNo ratings yet
- Example PHD Seminar - ENCS 8011Document23 pagesExample PHD Seminar - ENCS 8011Anthony ReyNo ratings yet
- AE 411 Module 7 - Two-Dimensional CharacteristicsDocument13 pagesAE 411 Module 7 - Two-Dimensional CharacteristicsJamilaWeinPerilloQuintanaNo ratings yet
- Lec 07-08 - FinalDocument32 pagesLec 07-08 - FinalNadeem ArainNo ratings yet
- ANS. MidtermDocument17 pagesANS. MidtermMohamed rabeaaNo ratings yet
- Lecture No, - 1week No, - 1course Code - BSI242 Noor BadshahDocument33 pagesLecture No, - 1week No, - 1course Code - BSI242 Noor BadshahLeo KhanNo ratings yet
- Technical Note - Autoregressive ModelDocument12 pagesTechnical Note - Autoregressive ModelNumXL ProNo ratings yet
- Application of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsFrom EverandApplication of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- Integer Optimization and its Computation in Emergency ManagementFrom EverandInteger Optimization and its Computation in Emergency ManagementNo ratings yet
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsFrom EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsNo ratings yet
- Paper 6 Efficient and Reliable Handling of Granulated Blast Furnace Slag PDFDocument16 pagesPaper 6 Efficient and Reliable Handling of Granulated Blast Furnace Slag PDFLarisa ChindrișNo ratings yet
- Date Received From Branch Reference Amount: Total Collections 371,905.17 Total Available Cash 527,546.92Document1 pageDate Received From Branch Reference Amount: Total Collections 371,905.17 Total Available Cash 527,546.92Merliza JusayanNo ratings yet
- BanKO Partner Outlet LocatorDocument344 pagesBanKO Partner Outlet LocatorBPI Globe BanKONo ratings yet
- Adobe Scan 02-Jul-2022Document4 pagesAdobe Scan 02-Jul-2022Akshita SethiNo ratings yet
- NSTP 2 Activity Plan BS Accountancy 1Document9 pagesNSTP 2 Activity Plan BS Accountancy 1JEnnie CanoNo ratings yet
- Detailed Advertisement English Nov22Document6 pagesDetailed Advertisement English Nov22VijayNo ratings yet
- Motor Policy: Ref. No. 170721117166 Date: Jul 16, 2021Document4 pagesMotor Policy: Ref. No. 170721117166 Date: Jul 16, 2021Rakshit Raj SinghNo ratings yet
- Economics B ComDocument9 pagesEconomics B ComIkram Ul Haq0% (1)
- Arup Scheme Design GuideDocument139 pagesArup Scheme Design GuideDean TyrrellNo ratings yet
- Summary For The Preparation of Bank Reconciliation StatementDocument5 pagesSummary For The Preparation of Bank Reconciliation StatementGhalib HussainNo ratings yet
- Precast Accessories Catalog 2022Document218 pagesPrecast Accessories Catalog 2022crvishnuramNo ratings yet
- Secular Outlook 2020-2029, YEAR III: Economic and Investment TrendsDocument24 pagesSecular Outlook 2020-2029, YEAR III: Economic and Investment TrendsGustavo KahilNo ratings yet
- Excel Problem Set 2 FIN 5203 SP21 PDFDocument3 pagesExcel Problem Set 2 FIN 5203 SP21 PDFAhmed MahmoudNo ratings yet
- Autocorrelation-Applied TestsDocument16 pagesAutocorrelation-Applied TestsAnsigar ChuwaNo ratings yet
- Kunci JWB Soal B 2015 PDFDocument29 pagesKunci JWB Soal B 2015 PDFAnisaa Okta100% (5)
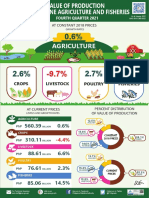
- Infographics, Value of Production in Philippine Agriculture and Fisheries, Fourth Quarter 2021Document1 pageInfographics, Value of Production in Philippine Agriculture and Fisheries, Fourth Quarter 2021Cart LaneNo ratings yet
- Cost AccountingDocument7 pagesCost AccountingShubhamNo ratings yet
- Peningkatan Kapasitas Pemerintahan Daerah Dalam Proses Masyarakat Ekonomi AseanDocument8 pagesPeningkatan Kapasitas Pemerintahan Daerah Dalam Proses Masyarakat Ekonomi AseanZex CeedNo ratings yet
- Course WATODocument81 pagesCourse WATOkmenciorNo ratings yet
- Ps B ABC and JitDocument4 pagesPs B ABC and JitMedalla NikkoNo ratings yet
- Presented Here Are Selected Transactions For Norlan Inc During SeptemberDocument2 pagesPresented Here Are Selected Transactions For Norlan Inc During SeptemberMiroslav GegoskiNo ratings yet
- Barro 2000 - Inequality and Growth in A Panel of CountriesDocument28 pagesBarro 2000 - Inequality and Growth in A Panel of Countriesbb_tt_AANo ratings yet
- Silver Members: Afghanistan Chamber of Commerce and IndustriesDocument78 pagesSilver Members: Afghanistan Chamber of Commerce and IndustriesHari BabuNo ratings yet
- SH Vikas Chaudhary Vs Unknown On 5 May 2021Document27 pagesSH Vikas Chaudhary Vs Unknown On 5 May 2021Mukesh NarayanNo ratings yet
- Plan de Formación para El Cuidado en Tiempos de Covid-19 (Agosto 2020) v1.0 (1-150)Document80 pagesPlan de Formación para El Cuidado en Tiempos de Covid-19 (Agosto 2020) v1.0 (1-150)leidy marcela mercado ibanezNo ratings yet
- The Art of Livin' Virtual Live Event - YouTubeDocument1 pageThe Art of Livin' Virtual Live Event - YouTubeViktor VorskiNo ratings yet
- Product Inventory - XLSX - May 2022Document1 pageProduct Inventory - XLSX - May 2022CRISTINE JOY LAUZNo ratings yet
- Lecture 5 Engineering Economics Interest Equivalence (Part 2) 1Document23 pagesLecture 5 Engineering Economics Interest Equivalence (Part 2) 1Natanael SiraitNo ratings yet
- TQMDocument21 pagesTQMMunaza SheraziNo ratings yet
- Toaz - Info Accounting by Carl S Warren James M Reeve Jonathan Duchac PRDocument80 pagesToaz - Info Accounting by Carl S Warren James M Reeve Jonathan Duchac PRJa DeNo ratings yet