Nonlinear Equation

NONLINEAR EQUATION
E LECTRONIC LECTURE
Hoang Hai Ha
HCMUT-OISP
Email: hoanghaiha@hcmut.edu.vn
August 30, 2023
Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 1 / 30

P ROBLEM
In this chapter, we seek roots of the following equation
x − 2−x = 0.
We need to answer the following questions:
1. How many roots does the equation have?
2. Locate the roots.
3. Find approximately the roots.

Step 1. Determine the number of roots.
The equation has ONLY ONE ROOT.

Step 1. Determine the number of roots.
The equation has ONLY ONE ROOT.

Locate the root: [0, 1] → The isolated interval containing root.

D EFINITION 1.1
The interval [a, b] is called the the isolated interval containing root of
the equation f (x) = 0 if there is only ONE real root on this interval.

D EFINITION 1.1
T HEOREM 1.1
Given an equation f (x) = 0 and an interval [a, b]. If f (x) is continous
on [a, b], f (a). f (b) < 0 and f is monotone on [a, b], then f (x) = 0 has
a unique real root on [a, b].

D EFINITION 1.1
T HEOREM 1.1
Given an equation f (x) = 0 and an interval [a, b]. If f (x) is continous
on [a, b], f (a). f (b) < 0 and f is monotone on [a, b], then f (x) = 0 has
a unique real root on [a, b].
E XAMPLE 1.1
Check that [0, 1] is the isolated interval containing root of x − 2−x = 0.
f (0) = −1, f (1) = 0.5;
f ′ (x) = 1 + 2−x ln 2 > 0 for all x ∈ [0, 1].

E RROR OF APPROXIMATE ROOT
T HEOREM 1.2 (G ENERAL FORMULA OF ERROR OF ROOT EQUATION )

Suppose that f (x) is continuous and differentiable on [a, b] and
∀x ∈ [a, b], | f ′ (x)| Ê m > 0. If equation f (x) = 0 has approximate root
x ∗ and exact root x, then the absolute error ∆x ∗ of x ∗ is:
| f (x ∗ )|
|x ∗ − x| É m
= ∆x ∗ .


| f (x ∗ )|
|x ∗ − x| É m
= ∆x ∗ .
E XAMPLE 1.2
Suppose that the equation f (x) = x 3 − 5x 2 + 12 = 0 has approximate
solution x ∗ = −1.37 on [−2, −1]. Estimate the error of x ∗ , rounding to
4 decimal digits.


| f (x ∗ )|
|x ∗ − x| É m
= ∆x ∗ .
E XAMPLE 1.2
Suppose that the equation f (x) = x 3 − 5x 2 + 12 = 0 has approximate
solution x ∗ = −1.37 on [−2, −1]. Estimate the error of x ∗ , rounding to
4 decimal digits.
Answer. ∆x ∗ ≈ 0.0034.

THE BISECTION METHOD

T HE BISECTION METHOD
Let equation f (x) = 0 have one real root on [a, b].


a0 + b0
Set a 0 = a, b 0 = b, x 0 = , d0 = b0 − a0
2


a0 + b0
Set a 0 = a, b 0 = b, x 0 = , d0 = b0 − a0
2
If f (x 0 ) = 0, we done. If not, there are 2 cases: if f (a 0 ) f (x 0 ) < 0,
then let a 1 = a 0 , b 1 = x 0 , otherwise, set a 1 = x 0 , b 1 = b 0 and
x 1 = (a 1 + b 1 )/2.


a0 + b0
Set a 0 = a, b 0 = b, x 0 = , d0 = b0 − a0
2
If f (x 0 ) = 0, we done. If not, there are 2 cases: if f (a 0 ) f (x 0 ) < 0,
then let a 1 = a 0 , b 1 = x 0 , otherwise, set a 1 = x 0 , b 1 = b 0 and
x 1 = (a 1 + b 1 )/2.
Reapply the process on [a 1 , b 1 ], [a 2 , b 2 ], ....., [a n , b n ].
At the n t h step, we get:
a + bn

 an É x É bn , an É xn = n
 É bn
2 .
 f (a n ). f (b n ) < 0, d n = b n − a n = b − a

2n
And x n is the approximate solution of equation.

T HE ERROR OF ROOT
T HEOREM 2.1
Let function f (x) be continuous and have unique solution x on [a, b] .
Then the bisection method generates a sequence {x n } that converges to
the exact solution x of f (x) = 0 with the error:
¯ ¯
¯ an + bn ¯ 1 b−a
|x n −x| = ¯
¯ −x¯¯ É (b n − a n ) = n+1 .
2 2 2

T HE ERROR OF ROOT
T HEOREM 2.1
Let function f (x) be continuous and have unique solution x on [a, b] .
Then the bisection method generates a sequence {x n } that converges to
the exact solution x of f (x) = 0 with the error:
¯ ¯
¯ an + bn ¯ 1 b−a
|x n −x| = ¯
¯ −x¯¯ É (b n − a n ) = n+1 .
2 2 2
E XAMPLE 2.1
Let the equation f (x) = 5x 3 − cos 3x = 0 have a unique root on [0, 1].
Using the bisection method to find x 4 and estimate its absolute error.

S OLUTION
n a n (−) b n (+) xn sign of f (x n )

0 0 1 0.5 +
1 0 0.5 0.25 -
2 0.25 0.5 0.375 -
3 0.375 0.5 0.4375 +
4 0.375 0.4375 0.40625

S OLUTION
n a n (−) b n (+) xn sign of f (x n )

0 0 1 0.5 +
1 0 0.5 0.25 -
2 0.25 0.5 0.375 -
3 0.375 0.5 0.4375 +
4 0.375 0.4375 0.40625
1
∆x 4 = 5 .
2

E XAMPLE 2.2
Let the equation f (x) = x − tan x = 0 have a root on [4, 4.5]. Using the
bisection method to find approximate solution which has error less
than 10−2 .

E XAMPLE 2.2
than 10−2 .
4.5 − 4
Find the least value n ∈ N such that ∆xn = < 10−2 .
2n+1

E XAMPLE 2.2
than 10−2 .
4.5 − 4
2n+1
n = 5.

E XAMPLE 2.2
than 10−2 .
4.5 − 4
2n+1
n = 5.
x 5 = 4.4921875.

T HE FIXED POINT METHOD
D EFINITION 3.1
A point x is called the fixed point of function g if g (x) = x

D EFINITION 3.1
From a given equation f (x) = 0, we always can define the equivalent

equation x = g (x) in many ways.

D EFINITION 3.1

E XAMPLE 3.1
Given the equation x 3 − x − 1 = 0 , we can rewrite:
x = x 3 − 1.

D EFINITION 3.1

E XAMPLE 3.1
x = x 3 − 1.
p
3
x = 1 + x.

D EFINITION 3.1

E XAMPLE 3.1
x = x 3 − 1.
p
3
x = 1 + x.
1 1
x = + 2.
x x

D EFINITION 3.1

E XAMPLE 3.1
x = x 3 − 1.
p
3
x = 1 + x.
1 1
x = + 2.
x x

T HEOREM 3.1
If g (x) is differentiable on [a, b], moreover
max |g ′ (x)| < 1

[a, b]
then g has exactly one fixed point on [a, b]. Function g is called
contraction mapping.

T HEOREM 3.1
If g (x) is differentiable on [a, b], moreover
max |g ′ (x)| < 1

[a, b]
then g has exactly one fixed point on [a, b]. Function g is called
contraction mapping.
E XAMPLE 3.2
Show that g (x) = (x 2 − 1)/3 has a unique fixed point on the interval
[−1, 1].

F IXED -P OINT I TERATION
Choose an initial value x 0 ∈ [a, b].

Construct the sequence by the formula x n = g (x n−1 ).


T HEOREM 3.2 (C ONDITION OF CONVERGENCE )

If function g is differentiable on [a, b] and q = |g ′ (x)| < 1, ∀x ∈ [a, b],
then for any x 0 ∈ [a, b], the sequence defined by x n = g (x n−1 )
converges to the unique fixed point x of g (x) in [a, b].


T HEOREM 3.2 (C ONDITION OF CONVERGENCE )

If function g is differentiable on [a, b] and q = |g ′ (x)| < 1, ∀x ∈ [a, b],
then for any x 0 ∈ [a, b], the sequence defined by x n = g (x n−1 )
converges to the unique fixed point x of g (x) in [a, b].
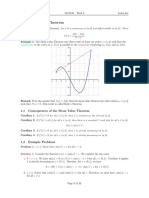
T HEOREM 3.3 (M EAN VALUE THEOREM )

If function f (x) is differentiable on (a, b), then there exists a point c in
(a,b) such that:
f (b) − f (a) = f ′ (c)(b − a).

Proof of Theorem 3.2
Applying the Mean value theorem
|x n − x| = |g (x n−1 ) − g (x)| = |g ′ (ζ1 )||x n−1 − x|

= |g ′ (ζ1 )||g (x n−2 ) − g (x)|
= |g ′ (ζ1 )||g ′ (ζ2 )||x n−2 − x|
≤ q 2 |x n−2 − x|.... ≤ q n |x 0 − x|.
Then lim x n = x.
n→∞

ERROR ESTIMATION
The priori error

qn
|x n − x| ≤ |x 1 − x 0 |.
1−q

ERROR ESTIMATION
The priori error

qn
|x n − x| ≤ |x 1 − x 0 |.
1−q
The posteriori error
q
|x n − x| ≤ |x n − x n−1 |.
1−q

E XAMPLE 3.3
5x 3 + 3
Let the equation x = = g (x) have unique root on (0, 1). Find
20
the approximate solution x 3 by the fixed point method and its error by
two formulas, x 0 is the midpoint on (0, 1).

E XAMPLE 3.3
5x 3 + 3
20
S OLUTION
1 x 0 = 0.5 → x 1 = 29/160 → x 2 = 0.151489(A) → x 3 = 0.150869(B )

E XAMPLE 3.3
5x 3 + 3
20
S OLUTION
1 x 0 = 0.5 → x 1 = 29/160 → x 2 = 0.151489(A) → x 3 = 0.150869(B )
q = max ¯ 3 x 2 ¯ = 3 (M )
¯ ¯
2
x∈[0, 1] 4 4

E XAMPLE 3.3
5x 3 + 3
20
S OLUTION
1 x 0 = 0.5 → x 1 = 29/160 → x 2 = 0.151489(A) → x 3 = 0.150869(B )
q = max ¯ 3 x 2 ¯ = 3 (M )
¯ ¯
2
x∈[0, 1] 4 4
q3
3 Priori error: ∆x 3 = 1−q |x 1 − x 0 | ≈ 0.5379

E XAMPLE 3.3
5x 3 + 3
20
S OLUTION
1 x 0 = 0.5 → x 1 = 29/160 → x 2 = 0.151489(A) → x 3 = 0.150869(B )
q = max ¯ 3 x 2 ¯ = 3 (M )
¯ ¯
2
x∈[0, 1] 4 4
q3
3 Priori error: ∆x 3 = 1−q |x 1 − x 0 | ≈ 0.5379
q q
4 Posterrior error: ∆x 3 = 1−q |x 3 − x 2 | = 1−q |B − A| ≈ 0.0019.

E XAMPLE 3.4
Using the fixed-point iteration method, find the approximate solution
5
x 3 of the equation x = 3 + 2 = g (x) on [3, 4] with x 0 = 3.5 and its
x
priori error .

E XAMPLE 3.4
Using the fixed-point iteration method, find the approximate solution
5
x 3 of the equation x = 3 + 2 = g (x) on [3, 4] with x 0 = 3.5 and its
x
priori error .
A NSWER
x 3 = 3.4248799, ∆x 3 = 0.0074103.

E XAMPLE 3.5
Using
p fixed point method, find the approximate root x 3 for equation
3
x = x + 1 = g (x) on [1, 2] with x 0 = 1.5 and compute its posteriori
error. Find the least number of steps of calculation to get the solution
whose priori error less then 10−3 .
dùng máy tính d/dx để tính đạo hàm cho nhanh

E XAMPLE 3.5
Using
p fixed point method, find the approximate root x 3 for equation
3
x = x + 1 = g (x) on [1, 2] with x 0 = 1.5 and compute its posteriori
error. Find the least number of steps of calculation to get the solution
whose priori error less then 10−3 .
x 3 ≈ 1.3259, ∆x3 ≈ 0.0014.

qn n 10−3 (1 − q)
The priori error ∆xn ≈ |x − x 0 | < 10−3
1−q 1
⇒q < ⇒
|x 1 − x 0 |
10−3 (1 − q)
n > l og q ≈ 3.3, thus n = 4.
|x 1 − x 0 |

E XAMPLE 3.6
Given the function x 4 + 2x 2 − x − 3 = 0. Transform it to the equivalent
equation x = g (x) in two cases below
p4
x = 3 + x − 2x 2
3x 4 + 2x 2 + 3
x=
4x 3 + 4x − 1
With the initial value x 0 = 1, which case gives us better approximate
solution?

E XAMPLE 3.6
Given the function x 4 + 2x 2 − x − 3 = 0. Transform it to the equivalent
equation x = g (x) in two cases below
p4
x = 3 + x − 2x 2
3x 4 + 2x 2 + 3
x=
4x 3 + 4x − 1
With the initial value x 0 = 1, which case gives us better approximate
solution?
n xn g 1 (x n ) g 2 (x n )
1 x1 1.1892 1.1429
2 x2 1.0801 1.1245
3 x3 1.1497 1.1241
4 x4 1.1078 1.1241

G EOMETRIC IDEA

F ORMULA CONSTRUCTION
Suppose that f (x) = 0 has unique root on [a, b].

Guess an initial value x 0 .


The tangent line equation to f (x) at x 0 is
y = f (x 0 ) + f ′ (x 0 )(x − x 0 ).


The tangent line equation to f (x) at x 0 is
y = f (x 0 ) + f ′ (x 0 )(x − x 0 ).
The intersection point between the tangent line and x-axis is
f (x 0 ) f (x 0 )
x = x0 − ′ , then x 1 = x 0 − ′ .
f (x 0 ) f (x 0 )
Repeat the process to find x 2 , x 3 , .., x n .
f (x n−1 )
Generate the sequence x n = x n−1 − ′ .
f (x n−1 )

E XAMPLE 3.7
Given the equation cos x − x = 0, using Newton’s method to find
approximate root on [0, π/2] after 3 iterations with initial guess is
x 0 = 0.

E XAMPLE 3.7
x 0 = 0.
S OLUTION
f = cos x − x, f ′ = − sin x − 1, set function
f (x) cos x − x
g (x) = x − ′ =x−
f (x) − sin x − 1

E XAMPLE 3.7
x 0 = 0.
S OLUTION
f (x) cos x − x
g (x) = x − ′ =x−
f (x) − sin x − 1
First iteration: x 1 = g (x 0 ) = 1

E XAMPLE 3.7
x 0 = 0.
S OLUTION
f (x) cos x − x
g (x) = x − ′ =x−
f (x) − sin x − 1
Second iteration: x 2 = g (x 1 ) = 0.750363867840244

E XAMPLE 3.7
x 0 = 0.
S OLUTION
f (x) cos x − x
g (x) = x − ′ =x−
f (x) − sin x − 1
Second iteration: x 2 = g (x 1 ) = 0.750363867840244
Third iteration: x 3 = g (x 2 ) = 0.739112890911362.

• Exactly root : A = 0.739085133
• B = x 2 = 0.750363867840244 /
• C = x 3 = 0.739112890911362

C ONVERGENCE
T HEOREM 3.4
The sequence x n generated by Newton’s method converges to exact root
x of function f (x) = 0 if the following conditions satisfy:
f ′ (x) ̸= 0, ∀x ∈ [a, b].

C ONVERGENCE
T HEOREM 3.4
f ′ (x) ̸= 0, ∀x ∈ [a, b].
f ′′ (x) is continuous on [a, b].

C ONVERGENCE
T HEOREM 3.4
f ′ (x) ̸= 0, ∀x ∈ [a, b].
f ′′ (x) is continuous on [a, b].
x 0 (initial guest) is sufficiently close to exact root x.

E XAMPLE 3.8
Given the equation f (x) = x 3 − 2x 2 − 5 on [−1, 4], construct the
sequence by Newton’s method with x 0 = −1 after 5 iterations.

E XAMPLE 3.8
Exact root x = 2.690647448028614.

x 1 = 0.142857142857143
x 2 = −9.731428571428571
x 3 = −6.276696653150196
x 4 = −2.398586261805698
x 5 = −1.270038382108753

E XAMPLE 3.8
Exact root x = 2.690647448028614.

x 1 = 0.142857142857143
x 2 = −9.731428571428571
x 3 = −6.276696653150196
x 4 = −2.398586261805698
x 5 = −1.270038382108753
⇒ Method failed

I NITIAL GUESS
Consider the equation f (x) = 0. Let f (x) be such that f ′ , f ′′ do not

change their signs on (a, b).
We will choose x 0 as below:
Taking any point p in (a, b)

I NITIAL GUESS

If f ′ (p) f ′′ (p) < 0, then we choose x 0 = a.

I NITIAL GUESS

If f ′ (p) f ′′ (p) > 0, then we choose x 0 = b.
or

I NITIAL GUESS

or
If f (a) f ′′ (a) > 0 then we choose x 0 = a.

I NITIAL GUESS

or
If f (a) f ′′ (a) > 0 then we choose x 0 = a.
If f (b) f ′′ (b) > 0 then we choose x 0 = b.

E RROR
E RROR
Estimate error of approximate root x n in Newton’s method is
| f (x n )|
|x n − x| É .
m

E XAMPLE 3.9
Let the equation f (x) = x 3 − 3x + 1 = 0 have a root on [0, 0.5]. Using
Newton method, find x 3 and its error.

E XAMPLE 3.9
S OLUTION
f ′ = 3x 2 − 3, f ′′ (x) = 6x

E XAMPLE 3.9
S OLUTION
f ′ = 3x 2 − 3, f ′′ (x) = 6x
Taking p = 0.1 ∈ [0, 0.5], check the sign of f ′ (x) f ′′ (x) at p:
f ′ (0.1) f ′′ (0.1) < 0, then choose x 0 = 0.

E XAMPLE 3.9
S OLUTION
f ′ = 3x 2 − 3, f ′′ (x) = 6x
f ′ (0.1) f ′′ (0.1) < 0, then choose x 0 = 0.
f (x) x 3 − 3x + 1
Consider g (x) = x − ′ =x− ,
f (x) 3x 2 − 3

E XAMPLE 3.9
S OLUTION
f ′ = 3x 2 − 3, f ′′ (x) = 6x
f ′ (0.1) f ′′ (0.1) < 0, then choose x 0 = 0.
f (x) x 3 − 3x + 1
Consider g (x) = x − ′ =x− , x n = g (x n−1 ).
f (x) 3x 2 − 3

E XAMPLE 3.9
S OLUTION
f ′ = 3x 2 − 3, f ′′ (x) = 6x
f ′ (0.1) f ′′ (0.1) < 0, then choose x 0 = 0.
f (x) x 3 − 3x + 1
f (x) 3x 2 − 3
x1 0.333333
x2 0.347222
x3 0.347296

E XAMPLE 3.9
S OLUTION
f ′ = 3x 2 − 3, f ′′ (x) = 6x
f ′ (0.1) f ′′ (0.1) < 0, then choose x 0 = 0.
f (x) x 3 − 3x + 1
f (x) 3x 2 − 3
x1 0.333333 Estimate of error

x2 0.347222 | f (x 3 )|
∆x 3 ≈ ≈ 2.5443 · 10−9 ,
x3 0.347296 m
where m = min | f ′ (x)| = | f ′ (0.5)| = 9/4.
x∈[0,0.5]

E XAMPLE 3.10
Given the equation sin x − e −x = 0, using Newton’s method to
1) Find approximate root x 3 on [0, 1] and estimate its error.
2) Find approximate root x n such that ∆xn < 10−6 .

E XAMPLE 3.10
S OLUTION
f ′ = cos x + e −x , f ′′ = − sin x − e −x .

E XAMPLE 3.10
S OLUTION
f ′ = cos x + e −x , f ′′ = − sin x − e −x .
since f (0) f ′′ (0) > 0 so we choose x 0 = 0.

E XAMPLE 3.10
S OLUTION
f ′ = cos x + e −x , f ′′ = − sin x − e −x .
x1 0.5
x2 0.585644
x3 0.588529

E XAMPLE 3.10
S OLUTION
f ′ = cos x + e −x , f ′′ = − sin x − e −x .
1) Estimate of error
x1 0.5 | f (x 3 )|
∆x 3 ≤ ≈ 6 · 10−6 ,
x2 0.585644 m
x3 0.588529 where m = min | f ′ (x)| = | f ′ (1)| =
x∈[0,1]
cos 1 + e −1 .
2) n = 4.

Nonlinear Equation

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Nonlinear Equation

Uploaded by

Copyright:

Available Formats

NONLINEAR EQUATION

August 30, 2023

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 1 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 2 / 30

The equation has ONLY ONE ROOT.

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 3 / 30

The equation has ONLY ONE ROOT.

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 3 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 4 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 4 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 4 / 30

T HEOREM 1.2 (G ENERAL FORMULA OF ERROR OF ROOT EQUATION )

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 5 / 30

T HEOREM 1.2 (G ENERAL FORMULA OF ERROR OF ROOT EQUATION )

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 5 / 30

T HEOREM 1.2 (G ENERAL FORMULA OF ERROR OF ROOT EQUATION )

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 5 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 6 / 30

Let equation f (x) = 0 have one real root on [a, b].

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 7 / 30

Let equation f (x) = 0 have one real root on [a, b].

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 7 / 30

Let equation f (x) = 0 have one real root on [a, b].

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 7 / 30

Let equation f (x) = 0 have one real root on [a, b].

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 7 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 8 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 8 / 30

n a n (−) b n (+) xn sign of f (x n )

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 9 / 30

n a n (−) b n (+) xn sign of f (x n )

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 9 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 10 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 10 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 10 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 10 / 30

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 11 / 30

From a given equation f (x) = 0, we always can define the equivalent

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 11 / 30

From a given equation f (x) = 0, we always can define the equivalent

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 11 / 30

From a given equation f (x) = 0, we always can define the equivalent

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 11 / 30

From a given equation f (x) = 0, we always can define the equivalent

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 11 / 30

From a given equation f (x) = 0, we always can define the equivalent

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 11 / 30

max |g ′ (x)| < 1

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 12 / 30

max |g ′ (x)| < 1

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 12 / 30

Choose an initial value x 0 ∈ [a, b].

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 13 / 30

Choose an initial value x 0 ∈ [a, b].

T HEOREM 3.2 (C ONDITION OF CONVERGENCE )

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 13 / 30

Choose an initial value x 0 ∈ [a, b].

T HEOREM 3.2 (C ONDITION OF CONVERGENCE )

T HEOREM 3.3 (M EAN VALUE THEOREM )

f (b) − f (a) = f ′ (c)(b − a).

Hoang Hai Ha (HCMUT) NONLINEAR EQUATION August 30, 2023 13 / 30

|x n − x| = |g (x n−1 ) − g (x)| = |g ′ (ζ1 )||x n−1 − x|