Scribd
Upload
33 views4 pages

Meal Frequency and Calorie Analysis

The document discusses frequency distributions and descriptive statistics for calories data from different meals. It computes percentiles, means, and standard deviations for calories for each meal type. It also examines outliers and plots histograms and bar charts to visualize the data distributions.

Uploaded by

Calvince Ambiro
Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
33 views4 pages

Meal Frequency and Calorie Analysis

The document discusses frequency distributions and descriptive statistics for calories data from different meals. It computes percentiles, means, and standard deviations for calories for each meal type. It also examines outliers and plots histograms and bar charts to visualize the data distributions.

Uploaded by

Calvince Ambiro
Copyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd

1.

Frequency distributions and percentile ranks

A. Using the Calories dataset, create a frequency distribution for the variable meal.

Table 1: Frequency Distribution Table For The Meal.


Statistics
Meal
N Valid 25
Missing 0
Mean 2.52
Median 3.00
Mode 3
Std. Deviation 1.122
Variance 1.260
Minimum 1
Maximum 4
Sum 63

Meal

Frequency Percent Valid Percent Cumulative

Percent

Valid Breakfast 6 24.0 24.0 24.0

Lunch 6 24.0 24.0 48.0

Dinner 7 28.0 28.0 76.0

Snack 6 24.0 24.0 100.0

Total 25 100.0 100.0


From the frequency distribution table above, dinner has the highest frequency compared

to other meals. The mean, mode, and median are 2.52, 3.00, and 3.00 respectively for the four

meals.

B. Compute the 20th, 40th, 60th, and 80th percentiles for the variable calories.

Table 2: 20th, 40th, 60th, and 80th percentiles for the calories.

Statistics
Calories
N Valid 25
Missing 0
Variance 13980.667
Minimum 80
Maximum 560
Percentiles 20 104.00
40 130.00
60 222.00
80 296.00
The 20 percentile is 104.00, 40th
th
percentile is 130.00, 60 percentile is 222.00, and 80th
th

percentile is 296.00 for variable calories.

2. Descriptive statistics for a single group


From the descriptive table above, the number of observations are 25, mean is 201.60,

median is 150.00, mode is 130, standard deviation is 118.20, maximum is 560, minimum is 80,

and range is 480.


3. Central Tendencies and Dispersion for Multiple Groups

Compute the mean and standard deviation of the variable calories for each meal. Report the

results in complete sentences.

4. Calculate z-scores: Determine the z-scores for calories. Are there calorie values more than 3

standard deviations away from the mean?

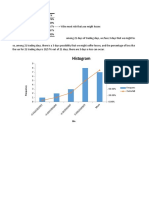
5. Histograms and Bar Charts

A. Plot the variable calories in a histogram.

B. Plot the variable meal using a bar chart.

6. Scatterplots: Construct a scatterplot to explore the relationship between cholesterol (X-axis)

and calories (Y-axis).

You might also like