Professional Documents
Culture Documents
Milne Thomson Method
Milne Thomson Method
Uploaded by
Ramkumar Mondal0 ratings0% found this document useful (0 votes)
8 views12 pagesOriginal Title
Milne_Thomson_Method (1)
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
8 views12 pagesMilne Thomson Method
Milne Thomson Method
Uploaded by
Ramkumar MondalCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 12
Milne-Thomson Method
Arpan Saha
UG 3rd Year
Ramakrishna Mission Vidyamandira
April 2, 2024
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 1 / 12
Table of Contents
1 Introduction
2 Analytic Functions
3 Working Rule
4 Examples
5 References
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 2 / 12
Introduction
This method was developed by Louis Melville Milne-Thomson (1937). It
helped greatly to simplify the process of finding an Analytic function
whose real or imaginary part is given.
Louis Melville Milne-Thomson
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 3 / 12
Analytic Functions
Definition
A function is said to be Analytic at a point if it is differentiable
everywhere in some neighborhood of the point.
A function is Analytic in a domain if it is analytic at every point in
the domain.
Example
1
The function f (z) = (z−1) is analytic at z = 1 + i.
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 4 / 12
Working Rule: To construct an Analytic Function by Milne
Thomson Method
Case 1: When u is given
Let f (z) = u(x, y ) + iv (x, y ) be analytic in a region D of C.
Let z = x + iy ∈ D. So, z̄ = x − iy .
So, x = z+z̄ z−z̄
2 , y = 2i .
This relation may be regarded as a formal identity in z and z̄.
Now, put z = z̄.
So, f (z) = u(z, 0) + iv (z, 0)
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 5 / 12
Working Rule: To construct an Analytic Function by Milne
Thomson Method (Continued)
Now, f ′ (z) = ux + ivx = ux − iuy . (By Cauchy-Riemann Equations)
Let ϕ1 (x, y ) = ux (x, y ) & ϕ2 (x, y ) = uy (x, y ).
Then f ′ (z) = ϕ1 (x, y ) − iϕR2 (x, y ) = ϕ1 (z, 0) − iϕ2 (z, 0).
Integrating we get, f (z) = (ϕ1 (z, 0) − iϕ2 (z, 0))dz + k.
Where k is an arbitrary constant
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 6 / 12
Working Rule: To construct an Analytic Function by Milne
Thomson Method (Continued)
Case 2: When v is given
Similar as previous. RTake f ′ (z) = −ify (x, y )
Integrating, f (z) = (ψ1 (z, 0) + iψ2 (z, 0))dz + h.
Where h is an arbitrary constant
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 7 / 12
Examples
Example 1 (When the real part is given)
If u = x 2 − y 2 , find a corresponding analytic function.
Let ϕ1 (x, y ) = ux (x, y ) = 2x, ϕ2 (x, y ) = uy (x, y ) = −2y .
So, ϕ1 (z, 0) = 2z, ϕ2 (z, 0) = 0
Therefore, f ′ (z) = ϕ1 (z, 0) − iϕ2 (z, 0) = 2z
So, f (z) = z 2 + c is the required analytic function,
Where c is an arbitrary constant.
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 8 / 12
Examples (Continued)
Example 2 (When the imaginary part is given)
Show that e x (xcosy − ysiny ) is a harmonic function. Find the analytic
function for which e x (xcosy − ysiny ) is the imaginary part.
Here, v = e x (xcosy − ysiny ).
So, vx = e x (xcosy − ysiny ) + e x cosy
vxx = e x (xcosy − ysiny + 2cosy )
vy = e x (−xsiny − ycosy − siny )
vyy = e x (−xcosy + ysiny − 2cosy )
So, vxx + vyy = 0
Hence, it is a harmonic function.
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 9 / 12
Examples (Continued)
let ψ1 (x, y ) = vy (x, y ), ψ2 (x, y ) = vx (x, y )
Therefore, f ′ (z) = i(ze z + e z )
So, f (z) = i(ze z ) + d, where d is an arbitrary constant
This is the required analytic function.
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 10 / 12
References
Ponnusamy, S., & Silverman, H. (2007). Complex variables with
applications. Springer Science & Business Media.
Kasana HS. Complex variables: theory and applications. PHI Learning
Pvt. Ltd.; 2005.
Milne-Thomson, L.M., 1937. On the relation of an analytic function
of z to its real and imaginary parts. The Mathematical Gazette,
21(244), pp.228-229.
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 11 / 12
Thank You!
Arpan Saha UG 3rd Year Milne-Thomson Method April 2, 2024 12 / 12
You might also like
- Wma12 01 Que 20240117Document32 pagesWma12 01 Que 20240117rumaiza100% (1)
- Galois Theory: Lectures Delivered at the University of Notre Dame by Emil Artin (Notre Dame Mathematical Lectures,From EverandGalois Theory: Lectures Delivered at the University of Notre Dame by Emil Artin (Notre Dame Mathematical Lectures,Rating: 4 out of 5 stars4/5 (5)
- Brijesh Laxman - A2 - MME IA-2Document2 pagesBrijesh Laxman - A2 - MME IA-2Tanay MathukiaNo ratings yet
- Module 4 Grade 11 General Math Ligutan Day 1Document3 pagesModule 4 Grade 11 General Math Ligutan Day 1anniezabateNo ratings yet
- Applications of The Newton Raphson Method in Decision Sciences and EducationDocument29 pagesApplications of The Newton Raphson Method in Decision Sciences and EducationRahul AkaNo ratings yet
- Complex Maths - 3Document99 pagesComplex Maths - 3Shail BajpaiNo ratings yet
- cmj313 321 ThomsonDocument10 pagescmj313 321 ThomsonsevynNo ratings yet
- Topology: DR S. SrinivasanDocument32 pagesTopology: DR S. SrinivasanKarunNo ratings yet
- A Very Slowly Convergent Sequence of Continuous FunctionsDocument3 pagesA Very Slowly Convergent Sequence of Continuous Functionsykw kcckcNo ratings yet
- Assignment 2Document1 pageAssignment 2harish nigamNo ratings yet
- 30 Days Maths SMS - AcDocument23 pages30 Days Maths SMS - AcPyae Sone KyawNo ratings yet
- Unit 3-Numerical Methods For Solving EquationsDocument20 pagesUnit 3-Numerical Methods For Solving Equationsyeswanth3604No ratings yet
- Mathanalysis1 04Document4 pagesMathanalysis1 04이태호No ratings yet
- Wald's Lemma' For Sums of Order Statistics of I.I.D. Random VariablesDocument14 pagesWald's Lemma' For Sums of Order Statistics of I.I.D. Random VariablesGuillermo MurilloNo ratings yet
- Computational Physics (PHY 362) : Dr. Muhammad KamranDocument57 pagesComputational Physics (PHY 362) : Dr. Muhammad KamranÛžrrFãrròqNo ratings yet
- Sumersión RiemannianaDocument20 pagesSumersión RiemannianaLUIS MANUEL VELAZQUEZ HERNANDEZNo ratings yet
- Sequences (Part 2)Document101 pagesSequences (Part 2)tejaswini muralidharanNo ratings yet
- Simmetries and Recursion Operators For Solution EquationDocument19 pagesSimmetries and Recursion Operators For Solution Equationdnse90900No ratings yet
- Ramanujan's Master Theorem: The Ramanujan Journal December 2012Document21 pagesRamanujan's Master Theorem: The Ramanujan Journal December 2012nisha chikuNo ratings yet
- Derivatives of Functions: Christian Caben M. LarismaDocument18 pagesDerivatives of Functions: Christian Caben M. LarismaEegnayb Majait CuizonNo ratings yet
- Chapter 7 Eigenvalues EigenvectorsDocument32 pagesChapter 7 Eigenvalues EigenvectorsMinh Duy LêNo ratings yet
- The Convergence of Quasi-Gauss-Newton Methods For Nonlinear ProblemsDocument12 pagesThe Convergence of Quasi-Gauss-Newton Methods For Nonlinear ProblemsMárcioBarbozaNo ratings yet
- A Note On Pseudo Operations Decomposable MeasureDocument5 pagesA Note On Pseudo Operations Decomposable MeasuretheijesNo ratings yet
- Limits Involving Trigonometric FunctionsDocument15 pagesLimits Involving Trigonometric FunctionsJenvent Matt50% (2)
- Fourrier Series NotesDocument31 pagesFourrier Series NotesVashish RamrechaNo ratings yet
- 7490 Dmth516 Topology IIDocument90 pages7490 Dmth516 Topology IInaughtydezireschdNo ratings yet
- ComplexDocument7 pagesComplexOmed HajiNo ratings yet
- Limit and Continuity of A Function: Nan Sing School of Cauayan City, IncorporatedDocument7 pagesLimit and Continuity of A Function: Nan Sing School of Cauayan City, IncorporatedJonathan Beltran Jr.No ratings yet
- Generalizations of Popoviciu's Inequality: Darij Grinberg Formal Version 4 March 2009Document40 pagesGeneralizations of Popoviciu's Inequality: Darij Grinberg Formal Version 4 March 2009Eddy StoicaNo ratings yet
- Spectral TheoremDocument8 pagesSpectral TheoremSoumyadeep DebNo ratings yet
- Tarea Ejercicios en InglesDocument6 pagesTarea Ejercicios en InglesJAir RCNo ratings yet
- Chapter 1 PDFDocument139 pagesChapter 1 PDFMaria Edenfe LeccionesNo ratings yet
- New Zealand Mathematical Olympiad Committee Convex FunctionsDocument7 pagesNew Zealand Mathematical Olympiad Committee Convex Functionsalphamale173No ratings yet
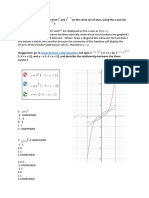
- What Happens If We Graph Both and On The Same Set of Axes, Using The X-Axis For The Input To Both and ?Document3 pagesWhat Happens If We Graph Both and On The Same Set of Axes, Using The X-Axis For The Input To Both and ?JakhongirNo ratings yet
- Lesson6 Functions04Document11 pagesLesson6 Functions04Anonymous SpyNo ratings yet
- Lecture 1: Introduction and Review of Prerequisite Concepts: DR Jay Lee Jay - Lee@unsw - Edu.auDocument33 pagesLecture 1: Introduction and Review of Prerequisite Concepts: DR Jay Lee Jay - Lee@unsw - Edu.auSean WilliamsNo ratings yet
- Math 1210 Signature Assignment - Paige PetersonDocument3 pagesMath 1210 Signature Assignment - Paige Petersonapi-317065066No ratings yet
- Nonlinear Least Squares Data Fitting: Appendix DDocument16 pagesNonlinear Least Squares Data Fitting: Appendix DTâm NguyễnNo ratings yet
- Metric SpacesDocument11 pagesMetric SpacesVibina JosephNo ratings yet
- SEEMOUS 2014 Contest ProblemsDocument1 pageSEEMOUS 2014 Contest ProblemsMitru CarmenNo ratings yet
- Lecture 23Document6 pagesLecture 23Syeda Farkhanda Batool NaqviNo ratings yet
- Section 6 - Projection Pursuit RegressionDocument23 pagesSection 6 - Projection Pursuit RegressionPeper12345No ratings yet
- AMAT 217 Final - Fall 2010Document16 pagesAMAT 217 Final - Fall 2010Stacy SmithNo ratings yet
- Finslerian Nonholonomic Frame For Matsumoto (α,β) -MetricDocument5 pagesFinslerian Nonholonomic Frame For Matsumoto (α,β) -MetricinventionjournalsNo ratings yet
- COMP 3250 B - Design and Analysis of Algorithms (Advanced Class)Document2 pagesCOMP 3250 B - Design and Analysis of Algorithms (Advanced Class)Z GooNo ratings yet
- Note Chapter 3 Mathematics (SM025)Document18 pagesNote Chapter 3 Mathematics (SM025)FATIN HANANI BINTI ROSLEE MoeNo ratings yet
- Mathematical Association of America The College Mathematics JournalDocument11 pagesMathematical Association of America The College Mathematics JournalJuan Andrés PérezNo ratings yet
- (Common To All Candidates) (Answer Questions) The Unit Normal To The Surface If Then 4 at The Point (2, - 2, 3)Document4 pages(Common To All Candidates) (Answer Questions) The Unit Normal To The Surface If Then 4 at The Point (2, - 2, 3)seeralan balakrishnanNo ratings yet
- Module 1 BCDocument6 pagesModule 1 BCJonathan Jr. BeltranNo ratings yet
- TOPOLOGY21Document12 pagesTOPOLOGY21himanshushrivastava2282001No ratings yet
- CH 05. Continuity & DiffnDocument4 pagesCH 05. Continuity & DiffnJanani M GowdaNo ratings yet
- 1-3.8 CalcDocument6 pages1-3.8 CalcJohn Seth Toribio SalazarNo ratings yet
- HKUST Math1013 Lecture02Document12 pagesHKUST Math1013 Lecture02JessicaLiNo ratings yet
- The Convergence Properties of The Credibility Distribution Sequence of Fuzzy VariablesDocument4 pagesThe Convergence Properties of The Credibility Distribution Sequence of Fuzzy VariablesSEP-PublisherNo ratings yet
- Functional Equations HandoutDocument6 pagesFunctional Equations HandoutMohamed MNo ratings yet
- Centroid of Area and Moment of Inertia CalculationDocument4 pagesCentroid of Area and Moment of Inertia CalculationsyakirohNo ratings yet
- Ma-6453 Probability and Queuing Theory - Anna University Important QuestionsDocument15 pagesMa-6453 Probability and Queuing Theory - Anna University Important QuestionsILYASNo ratings yet
- Elgenfunction Expansions Associated with Second Order Differential EquationsFrom EverandElgenfunction Expansions Associated with Second Order Differential EquationsNo ratings yet
- Differentiation (Calculus) Mathematics Question BankFrom EverandDifferentiation (Calculus) Mathematics Question BankRating: 4 out of 5 stars4/5 (1)
- Solving Systems of Linear Equations. Iterative MethodsDocument15 pagesSolving Systems of Linear Equations. Iterative MethodsJulija KaraliunaiteNo ratings yet
- CBSE Sample Paper For Class 9 Maths 2021 Set 1Document6 pagesCBSE Sample Paper For Class 9 Maths 2021 Set 1Aryaman TiwariNo ratings yet
- Grade 11 STEM PreCalculus 11F Week 1Document13 pagesGrade 11 STEM PreCalculus 11F Week 1CamilleTaylaranQuizonNo ratings yet
- NFEM Ch08Document14 pagesNFEM Ch08Rafael AbreuNo ratings yet
- 1 Strange AttractorsDocument28 pages1 Strange Attractorsduraiprakash83No ratings yet
- PrelimsDocument14 pagesPrelimsDeuter Abuso50% (2)
- Class 11 Maths Chapter 3 - Trigonometric FunctionsDocument53 pagesClass 11 Maths Chapter 3 - Trigonometric Functionsmr_agarwalNo ratings yet
- Learning Module 7: What Do You Need To Learn?Document12 pagesLearning Module 7: What Do You Need To Learn?Benedick Conrad R. GlifuniaNo ratings yet
- Fourier SeriesDocument12 pagesFourier SeriesBunga TulipNo ratings yet
- Implicit DifferentiationDocument11 pagesImplicit DifferentiationAna Marie ValenzuelaNo ratings yet
- Ordinary Differential Equations - Wronskian of $X 3$ and $X 2 - X - $ - Mathematics Stack ExchangeDocument3 pagesOrdinary Differential Equations - Wronskian of $X 3$ and $X 2 - X - $ - Mathematics Stack ExchangeKabilan SNo ratings yet
- 2nd Quarter Mathematics 7 CMDocument4 pages2nd Quarter Mathematics 7 CMJeff LacasandileNo ratings yet
- Chapter 7 - Poisson's and Laplace EquationsDocument11 pagesChapter 7 - Poisson's and Laplace EquationsmayankardeshanaNo ratings yet
- PartB Asymptotics&IntegralsDocument90 pagesPartB Asymptotics&Integralsyouness hidaNo ratings yet
- Integral Transform For EngineersDocument365 pagesIntegral Transform For EngineersLe Truong Duy100% (2)
- Midterm Complex AnalysisDocument16 pagesMidterm Complex AnalysisjhjoannaNo ratings yet
- Add Maths Practice Set 12Document6 pagesAdd Maths Practice Set 12Athanaseus ShazamNo ratings yet
- Fourier Transform: Exercise 1Document32 pagesFourier Transform: Exercise 1sreeyukthaNo ratings yet
- Hildreth 1957Document7 pagesHildreth 1957maryjarNo ratings yet
- Homework No. 4 ME 5113Document32 pagesHomework No. 4 ME 5113Nixon LagrisolaNo ratings yet
- 9709 w18 QP 31 PDFDocument20 pages9709 w18 QP 31 PDFFarhad AhmedNo ratings yet
- Mathematics: Quarter 1 - Module 1a: Illustrations of Quadratic EquationsDocument24 pagesMathematics: Quarter 1 - Module 1a: Illustrations of Quadratic EquationsJeng Bong Tan86% (7)
- Polynomial Roots - From Wolfram MathWorldDocument3 pagesPolynomial Roots - From Wolfram MathWorldAnonymous vVG64aC3No ratings yet
- Vertical CURVE 3 10102016Document28 pagesVertical CURVE 3 10102016Jf OngNo ratings yet
- Linear Equations in Two Variables: Grade 8 - MathematicsDocument29 pagesLinear Equations in Two Variables: Grade 8 - MathematicsDiana Rose GrumoNo ratings yet
- Exam 20131Document2 pagesExam 20131Argie AdduruNo ratings yet
- Chapter Content: Real Vector Spaces Subspaces Linear Independence Basis and Dimension Rank and NullityDocument47 pagesChapter Content: Real Vector Spaces Subspaces Linear Independence Basis and Dimension Rank and NullityBhavya SNo ratings yet