MECH 350 Instrumentation and Design of

Experiments

Assessing and presenting experimental data
Main topics
3 o principle and its application
The bound of uncertainty with confidence
level
Assessing Small Sample Sizes
Department of Mechanical Engineering and
Technology
Wentworth Institute of Technology
Gaussian Distributions
3 sigma (o) principle
If the random variable complies with the
normal distribution, the probability of the
Physical meaning of 3o principle in
measurement
If the measurement can be described by normal
distribution:
(1) Any measured value in the range (-3o, +3o)
has the probability of 99.74%. In other word,
any real measured value should or must be in
this range because the probability is 99.74%.
% 74 . 99 9974 . 0
2
1
exp
2
1
) 3 3 (
3
3 -
= =
(

|
.
|

\
|

= + < <
}
+
o

t o
o o
o
o
x
x P
(2) The probability of a measured value which is
larger than (+3o) or less than (-3o) is 0.0036
(0.36). That is, the chance of a real
measured value out of range (-3o, +3o) is
only 0.36%.
(3) If a real measured value out of range (-3o,
+3o) does happen, this measured value will
be rejected because of:
a) Something is wrong with the instrument, or
measurement system, or measurement setting, or
there was some mistake.
b) The measured parameter had significant change
due to machine setting.
In one word, There was some mistake during
measurement or the measured parameter was
not the same.
Application of the 3o principle in
measurement
The 3o principle is a tool to pre-analyze your
measured data to check whether the
measurement system and the experimental
setting is in normal status. If some data is
out the value range defined by 3o principle,
you should stop experiment and
measurement and find the possible causes
before you resume your experiment and
measurement. Otherwise, you will waste
your time because the measured data might
not be the data you intend to obtain.
Example: Followings were 20 measured sound levels (dBA) of
a type of machine:101.03; 100.98; 101.30; 100.98; 101.10;
101.25; 100.68; 100.75; 101.36; 101.67; 100.56; 100.85;
100.39; 101.25; 101.56; 101.23; 101.40; 100.95; 100.67;
100.56. The mean and standard deviation of these data
are 101.03 dBA and 0.35 dBA. Now, another 3 test data:
98.10, 101.45 and 103.89 were obtained. Are these three
measured data acceptable?
Solution:
Based on 6 o principle, the measured data should be in the
range (101.03-3X0.35=99.98, 101.03+3X0.35=102.08) with
the probability 99.74%.
The test data 98.10 was too low and should be rejected
(the cause for this was to use the wrong type of filter)
the test data 103.89 was too high and should be
rejected (the cause for this was to wrong RPM setting).
The test data 101.45 was normal and acceptable.
Application of probability theory in
measurement
Population vs. sample
Population: The set of
data (numerical or
otherwise)
corresponding to the
entire collection of units
about which information
is sought
Sample: A subset of the
population data that are
actually collected in the
course of a study.
In any real-life situation, we always deal with
samples from a population and not the population
itself.
Typically, our objectives for measurement are to
use measurement of sample to estimate:
a) the mean and standard deviation of the
population.
b) the bound of measured parameter with a
confidence level.
Since we normally use the average of the
measurement data to represent the measured
parameter, it is good to determine the bound of the
mean with a confidence level.
c) the bound of the mean with a confidence level.

The confidence intervals for measurement
If the measured parameter complies with normal
distribution and the sample number is big enough (>30),
the actual value of the measured parameter inside the
range (z
o/2
o, +z
o/2
o) will have the confidence level o
as listed in following table. -mean. o-standard deviation
Table 1 The confidence intervals
Confidence
level
85% 90% 95% 99%
Z
a/2
1.439 1.645 1.960 2.575
Bounds (-1.439o,
+1.439o)
(-1.645o,
+1.645o)
(-1.960o,
+1.960o)
(-2.575o,
+2.575o)
Z
a/2
can be determined by use of table 3.2 in page 50.
For example, probability level is 95%. Half of 0.95 is
0.475. From table 3.2, the z value for 0.475 is 1.960.

Example 1
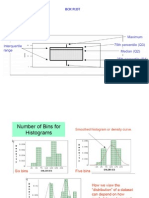
During a 12-hour test of a steam generator, the inlet
pressure was measured 100 times. The inlet pressure
should be held constant at 4.00 MPA. The results of a 12-
hour pressure test is shown in following table. (page 52).
The histogram is shown in following.
Pressure, p, in
MPA
Number of results,
m
(3.965,3.975)
(3.975,3.985)
(3.985,3.995)
(3.995,4.005)
(4.005,4.015)
(4.015,4.025)
(4.025,4.035)
(4.035,4.045)
(4.045,4.055)
1
3
12
25
33
17
6
2
1
The mean and standard deviation are =4.008 MPA,
o=0.014 MPA. For proper performance, the pressure
should no deviate from setting value 4.00 MPA by more
than about 1%.
(1) Determine the interval containing 95% of pressure
readings.
(2) Based on the test measurement, what is the probability
of pressure reading whose deviation from setting value
4.00MPA is less than 1%.
Solution:
(1) The probability level is 99%. From previous table, we
have Z
a/2
=2.575. The interval containing 99% of
pressure reading is:
(2.575o MPA)=(4.0082.575X0.014 MPA)
=(4.0080.036 MPA)
So, the interval containing 99% of pressure reading is:
(3.972, 4.044) MPA
The probability level for mean at
large samples (n>=30)
If the bias errors have been reduced to minimum
(proper calibration on the proper instrument with
proper measurement procedure), it is reasonable
to assume that the mean of the measurement is
very close to the true mean value in ideal
condition.

Now lets assess the uncertainty between the
measured mean and the true mean
If we do 100 measurement at one time, we
calculate the arithmetic average and will get
one value for the mean.
If we do another 100 measurement, we will get
another value of the mean, which will certainly
different from previous one.
If we repeat these kind of measurement, we would
obtain a set of samples for the mean. (this is
not the set of sample of measurement.)

Actually, we dont need to do above in order
to assess the uncertainty between the
measured mean and the true mean. We need
use one of probabilistic theory (Central limit
theorem).
Let us set a new random variable for
representing the mean:



x is the arithmetic average
n-is the sample size of the measurement
o is the standard deviation of the measurement

Here z is the random variable of mean and
still complies with normal distribution.

n
x x
z
x
o

o

=

=
Now let assume that we have a sample of
measurement. The sample size is n and the
mean is X and the standard deviation is S
x
.
Use the same concept in previous, we can get
the confidence intervals for mean with
probability level c%:





Z
c/2
can be obtained from table 1 in this lecture.


n
S
z x
n
S
z x
x
c
x
c 2 / 2 /
+ < <
Example 2 (cont.)
Determine a 99% confidence interval for the mean
pressure calculated in example 1.
Solution:
For the 100 pressure measurement, the mean and
standard deviation are 4.008 and 0.014 MPA. So
n=100, x=4.008 MPA, S
x
=0.014 MPA
For probability level of 99% from table 1, z
c/2
=2.575.
The intervals of mean pressure with probability level
99% is:

0036 . 0 008 . 4
100
014 . 0
575 . 2 008 . 4
2 /
= =
n
S
z x
x
c
Compare and notice the conceptual
difference
(1) The interval containing 99% of pressure
readings is: (expected range of measured
pressures)
(2.575o MPA)=(4.0082.575X0.014 MPA)
=(4.0080.036 MPA)
(2) The interval of mean pressure with probability
level 99% is: (Range of the true mean)

0036 . 0 008 . 4
100
014 . 0
575 . 2 008 . 4
2 /
= =
n
S
z x
x
c
Probability intervals for mean at
small samples (n<30)
When sample size is small (n<30), we will
not use normal distribution to describe the
mean random variable.

The probability theory proves that at this
time (n<30), the mean random variable
complies with t-distribution.
In figure v is degree of freedom. v=n-1. The
shape of t-distribution is similar to the normal
distribution. When v is big enough, the t-
distribution is the same as normal distribution.
The two-sided confidence interval for mean
x of a small sample (n<30) with probability
level c% is




Where o=1-c, v=n-1. The sample size is n and the
mean is X and the standard deviation is S
x
.
t
a/2, v
can be obtained from table 3.5 Students
t-distribution in page 58.

n
S
t x
n
S
t x
x
v c
x
v c , 2 / , 2 /
+ < <
Example 3
The 12 sound pressure-level measurement has mean
101.35 dBA and standard deviation 0.27 dBA. What is the
two-sided 95% confidence interval for the true mean
sound pressure-level?
Solution:
The required probability level is 95%, so o=1-0.95=0.05.
v=n-1=12-1=11. According to table 3-5 in page 58:
t
a/2, v
=t
0.025, 11
=2.201.
Hence the two-sided 95% confidence interval for sound
pressure level is:

53 . 101 17 . 101
11
27 . 0
201 . 2 35 . 101
11
27 . 0
201 . 2 35 . 101
, 2 / , 2 /
< <
+ < <
+ < <

n
S
t x
n
S
t x
x
v c
x
v c
Homework
Blackboard Assignments