Professional Documents
Culture Documents
Wave
Wave
Uploaded by
Ajay SinghCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Wave
Wave
Uploaded by
Ajay SinghCopyright:
Available Formats
Derivation of the Wave Equation
In these notes we apply Newtons law to an elastic string, concluding that small amplitude transverse vibrations of the string obey the wave equation. Consider a tiny element of the string. T (x + x, t) (x + x, t) u (x, t) x T (x, t) u(x, t)
x The basic notation is u(x, t) = vertical displacement of the string from the x axis at position x and time t (x, t) = angle between the string and a horizontal line at position x and time t T (x, t) = tension in the string at position x and time t (x) = mass density of the string at position x The forces acting on the tiny element of string are (a) tension pulling to the right, which has magnitude T (x + x, t) and acts at an angle (x + x, t) above horizontal (b) tension pulling to the left, which has magnitude T (x, t) and acts at an angle (x, t) below horizontal and, possibly, (c) various external forces, like gravity. We shall assume that all of the external forces act vertically and we shall denote by F (x, t)x the net magnitude of the external The mass of the element of string is essentially (x) x2 + u2 so the vertical component of Newtons law says that
u (x) x2 + u2 t2 (x, t) = T (x + x, t) sin (x + x, t) T (x, t) sin (x, t) + F (x, t)x
2
force acting on the element of string.
Dividing by x and taking the limit as x 0 gives ( x) 1 +
u 2 2 u x t2 (x, t)
= =
T (x, t) sin (x, t) + F (x, t) T (x, t) cos (x, t)
x (x, t)
(1) + F (x, t)
T x (x, t) sin (x, t) +
We can dispose of all the s by observing from the gure that tan (x, t) = lim
u x0 x
u (x, t) x
which implies, using the gure on the right below, that
u x (x, t)
sin (x, t) =
1+ (x, t) = tan1
2 u (x, t) x u x (x, t)
cos (x, t) = 1+
x (x, t)
1
2 u (x, t) x
1 + tan2 1
tan
= 1
2u x2 (x, t) 2 + u x (x, t)
Substituting these formulae into (1) give a horrendous mess. However, we can get considerable simplication by looking only at small vibrations. By a small vibration, we mean that | (x, t)| and hence that 1+
u 2 x
1 for all x and t. This implies that | tan (x, t)|
1, hence that
u x (x, t)
sin (x, t)
u x (x, t)
cos (x, t) 1
x (x, t)
2u x2 (x, t)
(2)
Substituting these into equation (1) give
u ( x) t2 (x, t) =
2
T u x (x, t) x (x, t)
u + T (x, t) x2 (x, t) + F (x, t)
(3)
which is indeed relatively simple, but still exhibits a problem. This is one equation in the two unknowns u and T . Fortunately there is a second equation lurking in the background, that we havent used. Namely, the horizontal component of Newtons law of motion. As a second simplication, we assume that there are only transverse vibrations. Our tiny string element moves only vertically. Then the net horizontal force on it must be zero. That is, T (x + x, t) cos (x + x, t) T (x, t) cos (x, t) = 0 2
Dividing by x and taking the limit as x tends to zero gives
x
T (x, t) cos (x, t) = 0
T (x, t) x
For small amplitude vibrations, cos is very close to one and
is very close to zero.
In other words T is a function of t only, which is determined by how hard you are pulling on the ends of the string at time t. So for small, transverse vibrations, (3) simplies further to
u u ( x) t2 (x, t) = T (t) x2 (x, t) + F (x, t)
2 2
(4)
In the event that the string density is a constant, independent of x, the string tension T (t) is a constant independent of t (in other words you are not continually playing with the tuning pegs) and there are no external forces F we end up with
2u (x, t) t2
= c2
2u (x, t) x2
where c=
T
You might also like
- Quiz-6 Answers and Solutions: Coursera. Stochastic Processes December 30, 2020Document4 pagesQuiz-6 Answers and Solutions: Coursera. Stochastic Processes December 30, 2020sirj0_hnNo ratings yet
- Soil InvestigationDocument12 pagesSoil InvestigationDerek AcalaNo ratings yet
- C1677 11aDocument3 pagesC1677 11adiego rodriguezNo ratings yet
- Note2 PDFDocument15 pagesNote2 PDFAvinash KumarNo ratings yet
- Brownian Motion and The Heat Equation: Denis Bell University of North FloridaDocument14 pagesBrownian Motion and The Heat Equation: Denis Bell University of North FloridaThuy Tran Dinh VinhNo ratings yet
- Today's Goal: X U X X (T) U (T)Document5 pagesToday's Goal: X U X X (T) U (T)Abdesselem BoulkrouneNo ratings yet
- Lecture10 - Pontryagins Minimum PrincipleDocument9 pagesLecture10 - Pontryagins Minimum PrincipleAmit BansodNo ratings yet
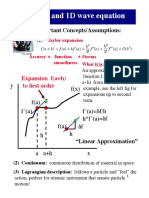
- Strings and 1D Wave Equation: Important Concepts/AssumptionsDocument17 pagesStrings and 1D Wave Equation: Important Concepts/AssumptionsOnur AkturkNo ratings yet
- Lecture 6: Introduction To Linear Dynamical Systems and ODE ReviewDocument13 pagesLecture 6: Introduction To Linear Dynamical Systems and ODE ReviewBabiiMuffinkNo ratings yet
- Lecture 6: Introduction To Linear Dynamical Systems and ODE ReviewDocument12 pagesLecture 6: Introduction To Linear Dynamical Systems and ODE ReviewBabiiMuffinkNo ratings yet
- Solutions HWA Chap 6 7Document8 pagesSolutions HWA Chap 6 7KenNo ratings yet
- L7 PH11003 22decDocument34 pagesL7 PH11003 22decDrashti ChoudharyNo ratings yet
- Lec 08-09Document6 pagesLec 08-09Alvaro Rafael MartínezNo ratings yet
- 1 Transverse Vibration of A Taut String: 1.138J/2.062J/18.376J, WAVE PROPAGATIONDocument4 pages1 Transverse Vibration of A Taut String: 1.138J/2.062J/18.376J, WAVE PROPAGATIONabolfazl sanchoolyNo ratings yet
- 1 The Hamilton-Jacobi-Bellman EquationDocument7 pages1 The Hamilton-Jacobi-Bellman EquationMakinita CerveraNo ratings yet
- Numerical PDEDocument12 pagesNumerical PDEsalkr30720No ratings yet
- Solution of Ordinary Differential Equations: 1 General TheoryDocument3 pagesSolution of Ordinary Differential Equations: 1 General TheoryvlukovychNo ratings yet
- 5.1. Derivation of The Wave EquationDocument21 pages5.1. Derivation of The Wave EquationAlejandro RodriguezNo ratings yet
- ECEN 314: Signals and Systems: 1 Continuous-Time ConvolutionDocument6 pagesECEN 314: Signals and Systems: 1 Continuous-Time ConvolutionJaanwar DeshNo ratings yet
- Lecture5 Worksheet SolnsDocument6 pagesLecture5 Worksheet Solnsjoanna.karczmarekNo ratings yet
- Pde - T6Q9Document2 pagesPde - T6Q9Bumi BumsNo ratings yet
- Taylor 2 DDocument5 pagesTaylor 2 DSumit AggarwalNo ratings yet
- Informal Derivation of Ito LemmaDocument2 pagesInformal Derivation of Ito LemmavtomozeiNo ratings yet
- Deterministic Continuous Time Optimal Control and The Hamilton-Jacobi-Bellman EquationDocument7 pagesDeterministic Continuous Time Optimal Control and The Hamilton-Jacobi-Bellman EquationAbdesselem BoulkrouneNo ratings yet
- PDE Textbook (101 150)Document50 pagesPDE Textbook (101 150)ancelmomtmtcNo ratings yet
- Stable Manifold ProofDocument4 pagesStable Manifold Proofanderjoe20No ratings yet
- 1 Continued... : Weston Barger August 7, 2016Document11 pages1 Continued... : Weston Barger August 7, 2016ranvNo ratings yet
- Mid Term Solutions PDFDocument2 pagesMid Term Solutions PDFMd Nur-A-Adam DonyNo ratings yet
- Wave EquationDocument18 pagesWave EquationBibekNo ratings yet
- Oscillations of A Hanging Chain: Math 3410, Spring Semester 2018Document5 pagesOscillations of A Hanging Chain: Math 3410, Spring Semester 2018Esteban BellizziaNo ratings yet
- 1 More Dispersion: Weston Barger June 30, 2016Document6 pages1 More Dispersion: Weston Barger June 30, 2016ranvNo ratings yet
- 2017optimalcontrol Solution AprilDocument4 pages2017optimalcontrol Solution Aprilenrico.michelatoNo ratings yet
- The Behaviour of The Wave Function Inside A Potential TunnelDocument2 pagesThe Behaviour of The Wave Function Inside A Potential TunnelAyman AmkassouNo ratings yet
- Oscillations of A Hanging Chain: Math 3510, Fall Semester 2019Document5 pagesOscillations of A Hanging Chain: Math 3510, Fall Semester 2019Kirti SaharanNo ratings yet
- Sample Paper: Math Comprehensive ExaminationDocument2 pagesSample Paper: Math Comprehensive ExaminationMansingh YadavNo ratings yet
- Wave EqnDocument15 pagesWave EqnALNo ratings yet
- Transmission of A Signals Through Linear SystemsDocument12 pagesTransmission of A Signals Through Linear SystemsRamoni WafaNo ratings yet
- Hyperbolic Equations: 8.1 D'Alembert's SolutionDocument10 pagesHyperbolic Equations: 8.1 D'Alembert's Solutionrohit singhNo ratings yet
- Principles of CommunicationDocument42 pagesPrinciples of CommunicationSachin DoddamaniNo ratings yet
- 1 D'alembert's Solution: Weston Barger July 12, 2016Document11 pages1 D'alembert's Solution: Weston Barger July 12, 2016ranvNo ratings yet
- EEE 303 HW # 1 SolutionsDocument22 pagesEEE 303 HW # 1 SolutionsDhirendra Kumar SinghNo ratings yet
- 4 - Stain TensorDocument12 pages4 - Stain TensorRishan Joshua DsilvaNo ratings yet
- The Wave Equation IIDocument3 pagesThe Wave Equation IIShahbaz KhanNo ratings yet
- Optimization Via The Hamilton-Jacobi-Bellman Method Theory and ApplicationsDocument9 pagesOptimization Via The Hamilton-Jacobi-Bellman Method Theory and ApplicationsYunli ShaoNo ratings yet
- Assignment 2b SolutionsDocument12 pagesAssignment 2b SolutionsvbweuhvbwNo ratings yet
- Fluid Mechanics AssignmentDocument10 pagesFluid Mechanics AssignmentabhijeetNo ratings yet
- Wave EquationDocument18 pagesWave Equationcoty mariNo ratings yet
- Func Anal HW p7Document3 pagesFunc Anal HW p7Tamás TornyiNo ratings yet
- Properties of The Wave Equation On RDocument12 pagesProperties of The Wave Equation On RElohim Ortiz CaballeroNo ratings yet
- Burgers Equation InviscidDocument19 pagesBurgers Equation InviscidSai Subrahmanyam PvkNo ratings yet
- Lesson 4Document10 pagesLesson 4Aram ShojaeiNo ratings yet
- Module-5 Convolution in Time and Frequency Domain Objective: To Understand The Importance of Convolution Operation in LTI SystemsDocument15 pagesModule-5 Convolution in Time and Frequency Domain Objective: To Understand The Importance of Convolution Operation in LTI SystemsMehul MayankNo ratings yet
- Lecture9 ImpedanceDocument10 pagesLecture9 ImpedanceYimy GarciaNo ratings yet
- Module 12 - Differential Equations 1Document7 pagesModule 12 - Differential Equations 1api-3827096No ratings yet
- Signals and Systems 02Document8 pagesSignals and Systems 02SamNo ratings yet
- Waveequation1 PDFDocument27 pagesWaveequation1 PDFAndrian RussuNo ratings yet
- Week 12Document15 pagesWeek 12Vu Quoc TrungNo ratings yet
- Note-Optimal Control Theory - From Surash P. SethiDocument5 pagesNote-Optimal Control Theory - From Surash P. SethiBereket HidoNo ratings yet
- 3 4 PontryaginDocument36 pages3 4 PontryaginAbdesselem BoulkrouneNo ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Tables of The Legendre Functions P—½+it(x): Mathematical Tables SeriesFrom EverandTables of The Legendre Functions P—½+it(x): Mathematical Tables SeriesNo ratings yet
- FieldsDocument14 pagesFieldsOmaar Mustaine RattleheadNo ratings yet
- 19 Rennes STNFSDocument51 pages19 Rennes STNFSOmaar Mustaine RattleheadNo ratings yet
- On The Number of Maximal Subgroups in A Finite Group: L.-K. LauderdaleDocument17 pagesOn The Number of Maximal Subgroups in A Finite Group: L.-K. LauderdaleOmaar Mustaine RattleheadNo ratings yet
- 1 P N p+1 N N N N P N N P NDocument2 pages1 P N p+1 N N N N P N N P NOmaar Mustaine RattleheadNo ratings yet
- Elliptic Curves: C H A P T E R 5Document26 pagesElliptic Curves: C H A P T E R 5Omaar Mustaine RattleheadNo ratings yet
- B N H N S N N K 0 KDocument12 pagesB N H N S N N K 0 KOmaar Mustaine RattleheadNo ratings yet
- A Scholar's Introduction To Stocks, Bonds and Derivatives: Martin V. Day June 8, 2004Document5 pagesA Scholar's Introduction To Stocks, Bonds and Derivatives: Martin V. Day June 8, 2004Omaar Mustaine RattleheadNo ratings yet
- Errata Michael Rosing - Implementing Elliptic Curve CryptographyDocument5 pagesErrata Michael Rosing - Implementing Elliptic Curve CryptographyOmaar Mustaine RattleheadNo ratings yet
- Stat 8501 Lecture Notes Baby Measure Theory Charles J. Geyer November 29, 2016 1 Old Probability Theory and NewDocument18 pagesStat 8501 Lecture Notes Baby Measure Theory Charles J. Geyer November 29, 2016 1 Old Probability Theory and NewOmaar Mustaine RattleheadNo ratings yet
- Volumes of Solids of Revolution. A Unified ApproachDocument7 pagesVolumes of Solids of Revolution. A Unified ApproachOmaar Mustaine RattleheadNo ratings yet
- IntroChains PDFDocument257 pagesIntroChains PDFOmaar Mustaine RattleheadNo ratings yet
- MATH 436 Notes: Functions and InversesDocument5 pagesMATH 436 Notes: Functions and InversesOmaar Mustaine RattleheadNo ratings yet
- Vipul Naik: (Result Stated)Document4 pagesVipul Naik: (Result Stated)Omaar Mustaine RattleheadNo ratings yet
- DR H Du DV V + H DW : Lines of Constant VDocument16 pagesDR H Du DV V + H DW : Lines of Constant VOmaar Mustaine RattleheadNo ratings yet
- VincentDocument130 pagesVincentOmaar Mustaine RattleheadNo ratings yet
- Uniform Continuity of Sinc XDocument8 pagesUniform Continuity of Sinc XOmaar Mustaine RattleheadNo ratings yet
- Le I78 Le I78 AY83 RW12 S 12: My WebsiteDocument7 pagesLe I78 Le I78 AY83 RW12 S 12: My WebsiteOmaar Mustaine RattleheadNo ratings yet
- (Ruffini's Rule) : 1) Synthetic Division: The ProcessDocument5 pages(Ruffini's Rule) : 1) Synthetic Division: The ProcessOmaar Mustaine RattleheadNo ratings yet
- Practica 6 FinalDocument25 pagesPractica 6 FinalOmaar Mustaine RattleheadNo ratings yet
- Protection and Switchgear by U.A.Bakshi and M.V.Bakshi PDFDocument389 pagesProtection and Switchgear by U.A.Bakshi and M.V.Bakshi PDFRutuja patilNo ratings yet
- SUZUKI DF40 50 Servisnaya InformatsiyaDocument8 pagesSUZUKI DF40 50 Servisnaya Informatsiyapaul_portegeNo ratings yet
- 2015 Logik 9 GBDocument2 pages2015 Logik 9 GBsebastianNo ratings yet
- En Visual Testing ProcedureDocument7 pagesEn Visual Testing ProcedureAdham AhmedNo ratings yet
- PROFIS Anchor 2.0.7Document4 pagesPROFIS Anchor 2.0.7Miky CastenNo ratings yet
- BACANI E101 Newtons 2nd Law of Motion Data SheetDocument2 pagesBACANI E101 Newtons 2nd Law of Motion Data SheetKurt BacaniNo ratings yet
- Adi Manual Treining Aeg ElectroluxDocument59 pagesAdi Manual Treining Aeg Electroluxbioteky100% (1)
- 2.1.2 Beam DeflectionDocument4 pages2.1.2 Beam DeflectionLuka VulinNo ratings yet
- Welding PlasticsDocument22 pagesWelding Plasticssav33No ratings yet
- W8L20 - Safety Spare Parts RecommendationDocument8 pagesW8L20 - Safety Spare Parts RecommendationTuan Linh VoNo ratings yet
- Tribology The Science of Combatting WearDocument33 pagesTribology The Science of Combatting Wearahmed titoNo ratings yet
- Kollmorgen TBM Frameless Motor Selection GuideDocument18 pagesKollmorgen TBM Frameless Motor Selection Guidejonan1991No ratings yet
- Biomedical Physics Lecture 1Document12 pagesBiomedical Physics Lecture 1Derrick VangennepNo ratings yet
- KTM Technical Handbook 7.0 Bomba Saturación NikuniDocument12 pagesKTM Technical Handbook 7.0 Bomba Saturación NikuniAnonymous w4ZnisPlazNo ratings yet
- Kartu Riwayat AlatDocument26 pagesKartu Riwayat AlatAwaluddin HanafieNo ratings yet
- United States PatentDocument10 pagesUnited States PatentendhylakausuNo ratings yet
- Calculation and Design of Bolted Connections: Structural Engineering Techniques Leeds Beckett UniversityDocument9 pagesCalculation and Design of Bolted Connections: Structural Engineering Techniques Leeds Beckett UniversityAhmet Selim ÇağinNo ratings yet
- Crankshaft Deflection MeasurementDocument7 pagesCrankshaft Deflection MeasurementJose OrtizNo ratings yet
- Seismic Performance of Emulative Precast Concrete Beam-Column Connections With Alternative Reinforcing DetailsDocument14 pagesSeismic Performance of Emulative Precast Concrete Beam-Column Connections With Alternative Reinforcing DetailsMălíķ ĂsfęnđýårNo ratings yet
- Cetex - ICS - Cabling DetailsDocument20 pagesCetex - ICS - Cabling DetailsPrasanna RamanathanNo ratings yet
- Bop 2FZ18-21 Rig202Document23 pagesBop 2FZ18-21 Rig202marthos ericson muñoz castilloNo ratings yet
- Column Interaction CurvesDocument58 pagesColumn Interaction Curvesdbircs1981No ratings yet
- Kinematics (Teachers)Document33 pagesKinematics (Teachers)Rajiv BiswasNo ratings yet
- Impulse Turbine (Fm60)Document6 pagesImpulse Turbine (Fm60)Mintesnot Abera100% (1)
- BJHL TFV00 0000 PRS Turbine Technical DescriptionDocument23 pagesBJHL TFV00 0000 PRS Turbine Technical Descriptionpavankumar001No ratings yet
- Line Sizing ManualDocument17 pagesLine Sizing ManualAkshay bhuranNo ratings yet
- Chapter 11 - V - Belts and V - Belt PulleysDocument62 pagesChapter 11 - V - Belts and V - Belt PulleysCésar Tapia100% (1)
- ALPHA Series BETA Series: Ac/Dc Inverter Tig DC InverterDocument1 pageALPHA Series BETA Series: Ac/Dc Inverter Tig DC InverterSajjad Rasheed QureshiNo ratings yet