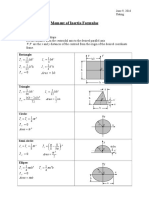
Useful Moment of Inertia Formulas

Note: In the table below, the overbar indicates the moment of inertia is taken about an axis that
passes through the centroid, denoted as C. Parallel axis theorems are:


2
Ad I I
x x
+ =
2
Ad I I
y y
+ = y x A I I
xy xy
+ =
Here, A is the area of the shape, d is the distance from the centroidal axis to the desired parallel
axis, and y x are the x and y distances of the centroid from the origin of the desired coordinate
frame.

Rectangle:
3
12
1
bh I
x
=
'

3
3
1
bh I
x
=
h b I
y
3
12
1
=
'
h b I
y
3
3
1
=
0 =
' y x
I Area = bh

Triangle:
3
36
1
bh I
x
=
'

3
12
1
bh I
x
=
72
) 2 (
2
h s b b
I
xy

= bh Area
2
1
=
( ) 3 2 s b x = 3 h y =
Circle:
4
4
1
r I I
y x
t = =
0 =
' y x
I
2
r Area t =
Semi-circle:
4
8
1
r I I
y x
t = =
4
'
9
8
8
r I
x
|
.
|

\
|
=
t
t

0 =
' y x
I
2
2
r
Area
t
=
Ellipse:
3
4
1
ab I
x
t = b a I
y
3
4
1
t =
0 =
' y x
I
ab Area t =

y
x
y`
x`
b
h
C
b/2
h/2
b
h
x
x`
C
h/3
s
C
r
y
x
C
r
y
x
4r/3
x`
C
r
y
x
a
b