Aci Rectangular Tanks2010

UWU/Civil&EnvironmentalEngineeringCVNG3016DesignofEnvironmentalEngineeringSystems
2010
CVNG 3016 DESIGN OF ENVIRONMENTAL SYSTEMS

TOPIC:
Design of Reinforced Concrete Liquid Retaining Structures
LECTURER: Dr.WilliamWilson
DESIGNOFREINFORCEDCONCRETETANKS(ACI318/ACI350)
Recommended Reading:
A. Codes
1. ASCE7-05 - Minimum Design Loads for Buildings and other Structures
2. ACI 318-06 Building Code requirements for Reinforced Concrete
3. ACI 350R 06 Environmental Engineering Concrete Structures.
B. Technical Literature
1. Munshi, Javeed A. Rectangular Concrete Tanks (Rev. 5th Ed.), Portland Cement
Association, 1998.
2. Portland Cement Association, 1992. Underground Concrete Tanks
3. Portland Cement Association, 1993. Circular Concrete Tanks without prestressing
RECTANGULARTANKS
DesignConsiderations
Flexure
bendinginwallsandbase
Shear
- wall-to-base, wall-to-wall junctions
Tension
- horizontal tension in walls, base
Deflection
vertical/ horizontal deflections of wall
Cracking
Flotation
thermal, flexural, tension cracks
- when base is located below water table level
Base Fixity - (i) Fixed (ii) Pinned

LoadingConditions
Condition 1 Condition 2 Condition 3 -
in reality neither of these

conditions may actually exist
Both may need to be investigated
Internal Water Pressure only (before backfilling, i.e. leakage test)

External Earth Pressure only (before filling tank)
Tank full and Soil backfilled (resistance provided by soil is ignored)
1
2010
Moments
pinned base
fixed base
+
Fv
(a) Liquid pressure in Tank
Fv
Ft
(b) Vertical Forces
Fv
M (-)
Fv
Ft
Ft
M (+)
Fv
(shear)
Ft
M
Fv
M (-)
Fv
Fv
(c) Horizontal Forces
FIGURE 1 FORCES IN RECTANGULAR TANK WALLS
2010
STRENGTHDESIGNMETHOD
Basic Requirement:
Design Strength Required Strength
(Nominal Strength) U
Rn U
(ACI 318 Sect. 9.2)
U = 1.4 (D + F)
(2.1)
(ACI 350 cl. 2.6.5)
U = 1.7 (D + F)
(2.2)
D = dead load
F = liquid pressure
Sanitary Durability Factors - ACI 350 applies sanitary durability factors (based on crack width
calculations) to obtain the Required Strength
Required Strength = Sanitary Coefficient x U
Ur = Cs x U
(2.3)
Sanitary Coefficients are:

(bending)
Cs = 1.3
Cs = 1.65
(direct tension / hoop tension)
Cs = 1.3
(shear beyond shear capacity of concrete stirrup design)
Cs = 1.0
(concrete shear)
Strength Design Requirements

(a) Flexural Reinforcement
Design Strength 1.3U
Mn 1.3(1.4MD+ 1.7 ML+1.7 MF)
(2.4)
(b) Direct Tension Reinforcement

Design Strength 1.65U
Nn 1.65(1.4ND+ 1.7NL+1.7NF)
(2.6)
2010
(c) Stirrup Shear Reinforcement

Design Strength 1.3 (Vc - Vc)
Vs 1.3 (Vu - Vc)
(2.7)
(d) Concrete Shear and Compression Reinforcement

Design Strength 1.0 U
Vn 1.0Vu
(2.8)
(e) Minimum reinforcement (ACI 318-05 cl. 10.5)
As, min =
f c
fy
b w d 200
(f) Minimum cover = 2 in.
bw d
fy
Concrete sections with t 24 use

minimum
temperature
and
(2.9)
shrinkage reinforcement at each
face based on 12 thickness.
Size of rebar #11
Max. spacing of rebar 12
Minimum cover in tank walls = 2
(g) Minimum thickness for walls over 10 ft. high = 12 ins.
Serviceability for Normal Sanitary Exposure (ACI 350, cl. 2.6.6)

Crack Control
Maximum Design crack width
Severe exposure
Aesthetics
= 0.010 in.
= 0.008 in.
Crack width calculation is based on the following equation:
z=f s 3 d c A
(2.10)
Where,
Z is a quantity limiting distribution of flexural reinforcement
(ACI 350 limits)
z 115 kips/in
(crack width = 0.010 in)
z 95 kips/in
(crack width = 0.008 in)
2010
fs = calculated stress in reinforcement at service loads, ksi

dc = concrete cover to centroid of closest rebar
A = effective area of concrete surrounding flexural reinforcement with same
centroid divided by the number of bars, in2.
The maximum spacing it given by,
Z3
bw = 2 3
2d c f s
(2.11)
A= 2dcbw
t
dc
bw
Fig. 1.0 - Calculation of A
EXAMPLE 1
2010
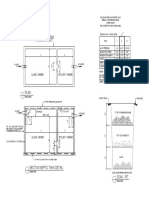
RectangularTank
20'-0
10'-0
30'-0
2.5'
Cross Section
350
20'-0
Longitudinal Section
30'-0
Plan
Fig. E1 Plan and sections of Tank
Design Data
Weight of Liquid, w =
70 lbs/ft3
Weight of Soil, s =
100 lbs/ft3
=
0.3
ka
'
=
4000 psi
fc
fy
=
60,000 psi
Wall thickness, t
=
18 in.
Base slab projection beyond wall = 2.5 ft.
Water pressure at base,
p = wa = 70 x 10 = 700 lbs/ft2
6
2010
DesignforVerticalBendingMoments
Wall considered fixed at base and free at top
Using PCA Charts to calculate moments (Table 3-29: case 3 Long side)
Ratio of length/height = b/a = 30/10 = 3.0 (long side)
Ratio of width/height = c/a = 20/10 = 2.0 (short side)
Mx = CMx x pa2/1000
= CMx x 700 x 102 / 1000

= CMx x 70 ft-lbs
= CMx x 0.84 in-kips
For sanitary structures
Mu = Sanitary coef x 1.7 x M
Mux = 1.3 x 1.7 x Mx
Mux = 1.3 x 1.7 x CMx x 0.84 in-kips
= 1.86 x CMx
Maximum positive moment at 0.7 a
(CMx = +10) Mux = +18.6 kips-in
Maximum negative moment at bottom (CMx = -129) Mux = -239.9 kips-in
a = 10'
M = + 18.6 kips-in
V = 3500 lbs
M = - 239.9 kips-in
Fig E2 Vertical Moments at mid-length

Assuming No. 5 bars at 12in. c/c
Cover = 2 in.
Wall thickness = 18 in.
d = 18 2 5/16 = 15.7 in.
(db = 5/8 in.)

7
f c bd
239.9
0.9x4x12x (15.7 )
(From Appendix A)
A s =bd
2010
=0.0225
= 0.023
f c'
4
= 0.023x12x15.7x
= 0.29in 2
fy
60
Checkminimumsteel (ACI 318-05 cl. 10.5)
fc'
4000
x12x15.7=0.595in 2 200 bwd/fy
fy
60000
200b w d 200x12x15.7
=
=
=0.628in 2 (governs)
fy
60,000
Asmin =
bw d=
(ACI 318 -05 cl. 10.5.3)
Use 4/3 of As required by analysis
As = 4/3 x 0.29 = 0.39in2
Provide No. 5 @ 9 in c/c on inside face (As =0.41 in2)

DesignforHorizontalBendingMoments
2590 lbs
2590
-65.6 in-kip
1890 lbs
-65.6
1890
1890
2590
2590
+35.93 in-kip
+35.93
1890
-65.6
1890
-65.6
1890 lbs
2590
2590
Fig. E3- Horizontal Forces (un-factored) at mid-height of tank)

NB: Shear Forces calculations on Page 9 below
8
(a)
2010
At Corner - Horizontal Moment Steel
Muy = 1.3 x 1.7 x 65.66

Muy = 145.1 in-kips
Mu
145.1
=
=0.0136
1
2
f c bd 0.9x4x12x15.7 2
(From Appendix A)
= 0.014
A s =bd
(b)
f c'
4
=0.014x12x15.7x
=0.18in 2
fy
60
Steel required for Direct Tension in Long Wall

Factored tension Nu = 1.65 x 3213 = 5301 lbs/ft width
As=
Nu
5301
=
=0.1in 2
0.9f y 0.9x60,000
Direct tension steel is equally distributed on inside and outside faces of wall.
Total steel required on inside face =
As,min =
0.18+
0.1
=0.23in 2
2
200b w d
=0.625in 2 (governs)
fy
4/3 of As required by analysis = 4/3 x 0.23 = 0.31 in2

Provide No.5 @ 12 in (As = 0.31 in2) horizontal steel on inside face of long walls.
(c)
2010
Horizontal steel near centre of outside face of wall

Design for M = 40.91 in-kips
(d)
CrackControl - Check Maximum Spacing of bars

Maximum un-factored moment
M=
239.9
=108.6in-kips
(1.7x1.3)
Stress in steel reinforcement

M
A s jd
As = 0.41 in2/ft
fs =
n=
29,000
57
4000
d = 15.7 in
=8
0.41
= 0.00218
(12 x 15.7 )
k = 2 n + ( n ) n = 0.17
2
j = 1 k/3 = 0.94
fs =
108.6
=17.95ksi
0.41x0.94x15.7
z3
s m ax =
( 2 x d c2 x f s3 )
dc = cover +
2
z = 115 kips/in
= 2 + 0.313=2.313in
fs = 17.95 ksi
115 3
s max =
=24.6in>9in
2x2.313 2 x17.95 3
OK
10
2010
DesignforShearForces
Using PCA Charts to calculate moments (Table 2-17: CASE 3 Long side)
Ratio of length/height = b/a = 30/10 = 3.0 (long side)
Ratio of width/height = c/a = 20/10 = 2.0 (short side)
Shear, V = Cs x p x a
(a)
Check Shear at bottom of Wall

Maximum shear at bottom of long wall,
V = 0.50 x 700 x 10 = 3500 lbs
Vu =1.7x3500=5950 lbs
Since tensile force from adjacent wall is small
Vc =2 fc' bd
=2 4000x12x15.7 = 23,831 lbs
Vc = 0.85 x 23,831= 20,256lbs > 5950 lbs
(b)
OK
Check Shear at side edge of long wall

V = 0.37 x 700 x 10 = 2590 lbs
Vu = 1.7 V = 1.7 x 2590 = 4403 lbs
Wall subjected to simultaneous tensile force due to shear in short side wall;
(ACI 318 cl.11.3.2.3) gives allowable shear as:
Nu
V c = 2 1+
500A g
f c' b d
Nu = tension in long wall due to shear in short wall.

Shear in short side wall V = 0.27 x 700 x 10 = 1890 lbs.
11
2010
Nu = -1.7 x 1890 = -3213 lbs

Ag = 18 x 12 = 216 in2
-3213 1
Vc =2 1+
f c bd
500x216
=1.94 4000x12x15.7 = 23,116 lbs
Vc = 0.85 x 23,116 = 19,649 lbs > 4403 lbs

OK
(e)
ShrinkageandTemperatureReinforcement
Assuming the walls will be in one pour of 30 ft long.
Minimum Temperature and Shrinkage reinforcement
(Fig 1-2)
A st
=0.0033
bh
1
A st = x12x18=0.356in 2 (No. 5 @ 10)
2
< 0.41 in2
(No. 5 @ 9)
OK
SummaryofReinforcement
Inside face vertical
Outside face vertical
Inside face horizontal
Outside face horizontal
No. 5 @ 9 in
No. 5 @ 10 in (Use No. 5 @ 9 in for consistency)
No. 5 @ 12 in
No. 5 @ 12 in
12
2010
BASESLABDESIGN
Design as a 2-way spanning slab, simply supported at edges.
Assume that the pressure beneath the slab is uniform and is generated by the weight
of the walls spread over entire area.
12
10'
30'
Vs = 4150 lbs
3500 lbs
Vls
Mls = 8497 ft-lb
2500 lbs
Mss = 15,413 ft-lb
2500 lbs
3500 lbs
k
Fig E4 Forces on Base Slab
Unit weight of concrete = 150 lbs/ft3
13
2010
Wall Dead load = 150 ( 2 x 1.5 x 10 x ( 30 + 0.75) + ( 20+0.75) ) = 231,750 lbs

Factored DL = 1.4(231,750) = 324,450 lbs
324,450
p=
= 509 lbs/ft 2
( 30.75 x 20.75)
Using PCA Tables
Mss (short span)
Mls (long span)
Vss
Vls
Ft (long span)
=
=
=
=
=
78 x 509 x 202 /1000

43 x 509 x 202 / 1000
0.24 x 509 x 20
0.42 x 509 x 20
0.4 x 700 x 10
= 15,881 ft-lb = 191 in-k

= 8755 ft-lb = 105in-k
= 2443 lbs = 2.4 k
= 4276 lbs = 4.3 k
= 2800 lbs
Design of Short Span
2.4k
12
191 in-k
3.5 k
Assume slab thickness, h = 12 ins.

For #6 bars and 2 cover
d = 12 2 0.75/2 = 9.625 ins.
Short Span
(a)
Mid-span Moment Steel

(NB: ACI 350 is silent on use of sanitary coefficient for slabs, but we will apply
same here)
Muy = 1.3 x 191
Muy = 248.3 in-kips
Mu
248.3
=
= 0.062
'
2
fcbd 0.9 x 4 x 12 (9.625)2
(From Appendix A)
14
2010
= 0.064
f c'
4
A s =bd =0.064 x 12 x 9.7x
= 0.49in 2
fy
60
(b)
Steel required for Direct Tension in short span

As=
Nu
5775
=
=0.11in 2
0.9f y 0.9x60,000
Direct tension steel is equally distributed on inside and outside faces of slab.
Total steel required on top face =
As,min =
0.49+
0.11
=0.55 in 2
2
200b w d 200 (12 x 9.7 )

=
= 0.39 in 2
fy
60000

Provide No.6 @ 7 in crs.
direction.
(As = 0.75 in2) steel on top face of slab in short
(c) Long Span

Muy = 1.3 x 105 in-kips
Muy = 136.5 in-kips

d = 12 -2 -0.625- 0.625/2 = 9.0625
Mu
136.5
=
= 0.0385
1
2
fc bd 0.9 x 4 x 12 x 9.06252
(From Appendix A)
= 0.039
15
2010
f c'
4
A s =bd =0.039 x 12 x 9.0625x
= 0.283 in 2
fy
60
Steel required for Direct Tension in long span
As=
Nu
4620
=
=0.085in 2
0.9f y 0.9x60,000
Direct tension steel is equally distributed on inside and outside faces of slab.
Total steel required on top face =
As,min =
0.283+
0.085
=0.326 in 2
2
200b w d 200 (12 x 9.7 )

=
= 0.39 in 2 (governs)
fy
60000

Provide No.5 @ 8 in crs
(b)
Check Shear at side edge of long span

V = 4276 lbs
Vu = 1.0 V = 4276 lbs
Wall subjected to simultaneous tensile force (ACI 318 cl.11.3.2.3) gives allowable
shear as:
Nu
V c = 2 1+
500A
g
f c' b d
Nu = 3500 lbs
Ag = 12 x 12 = 144 in2
16
2010
-3500 '
Vc =2 1+
fc bd
500 x 144
=1.90 4000x12 x 9.7= 14,008 lbs
Vc = 0.85 x 14,008 = 11,907 lbs > 4276 lbs

OK
(e)
ShrinkageandTemperatureReinforcement
Assuming the walls will be in one pour of 30 ft long.
Minimum Temperature and Shrinkage reinforcement
(Fig 1-2)
A st
=0.0033
bh
1
A st = x 0.0033x12x12=0.238 in 2
2
< 0.73 in2
OK
Summary of Reinforcement
Top face short direction (mid-span)
Top face short direction (edges)
Top face - long direction (mid-span)
Bottom face - both direction (edges)
Bottom face both direction (mid-span)
No. 6 @ 7 in crs
No. 5 @ 7 in crs (for consistency)
No. 5 @ 7 in (for consistency)
No. 5 @ 7 in
No. 5 @ 12 in
17
2010
RectangularTank
No. 5 @ 10 in c/c
No. 5 @ 12 in. c/c
No. 5 @ 12 in. c/c
No. 5 @ 10 in c/c
No. 5 @ 9 in. c/c

Water
stop
No. 6 @ 7 in. c/c

No. 5 @ 7 in. c/c
Water stop
No. 5 @ 7 in. c/c both ways
Section showing Reinforcement Details for Rectangular Tank
Dr. William Wilson

17 March 2010
18

Aci Rectangular Tanks2010

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Aci Rectangular Tanks2010

Uploaded by

Copyright:

Available Formats

UWU/Civil&EnvironmentalEngineeringCVNG3016DesignofEnvironmentalEngineeringSystems

CVNG 3016 DESIGN OF ENVIRONMENTAL SYSTEMS

Design of Reinforced Concrete Liquid Retaining Structures

- wall-to-base, wall-to-wall junctions

- horizontal tension in walls, base

vertical/ horizontal deflections of wall

thermal, flexural, tension cracks

- when base is located below water table level

Base Fixity - (i) Fixed (ii) Pinned

in reality neither of these

Internal Water Pressure only (before backfilling, i.e. leakage test)

(b) Vertical Forces

FIGURE 1 FORCES IN RECTANGULAR TANK WALLS

(ACI 350 cl. 2.6.5)

Sanitary Coefficients are:

Strength Design Requirements

(b) Direct Tension Reinforcement

(c) Stirrup Shear Reinforcement

(d) Concrete Shear and Compression Reinforcement

(e) Minimum reinforcement (ACI 318-05 cl. 10.5)

(f) Minimum cover = 2 in.

Concrete sections with t 24 use

(g) Minimum thickness for walls over 10 ft. high = 12 ins.

Serviceability for Normal Sanitary Exposure (ACI 350, cl. 2.6.6)

Maximum Design crack width

Crack width calculation is based on the following equation:

fs = calculated stress in reinforcement at service loads, ksi

Fig. 1.0 - Calculation of A

= CMx x 700 x 102 / 1000

Fig E2 Vertical Moments at mid-length

(db = 5/8 in.)

Checkminimumsteel (ACI 318-05 cl. 10.5)

(ACI 318 -05 cl. 10.5.3)

Use 4/3 of As required by analysis

As = 4/3 x 0.29 = 0.39in2

Provide No. 5 @ 9 in c/c on inside face (As =0.41 in2)

Fig. E3- Horizontal Forces (un-factored) at mid-height of tank)

At Corner - Horizontal Moment Steel

Muy = 1.3 x 1.7 x 65.66

Steel required for Direct Tension in Long Wall

4/3 of As required by analysis = 4/3 x 0.23 = 0.31 in2

Horizontal steel near centre of outside face of wall

CrackControl - Check Maximum Spacing of bars

Stress in steel reinforcement

Check Shear at bottom of Wall

Vc = 0.85 x 23,831= 20,256lbs > 5950 lbs

Check Shear at side edge of long wall

Nu = tension in long wall due to shear in short wall.

Nu = -1.7 x 1890 = -3213 lbs

Vc = 0.85 x 23,116 = 19,649 lbs > 4403 lbs

Mls = 8497 ft-lb

Mss = 15,413 ft-lb

Fig E4 Forces on Base Slab

Unit weight of concrete = 150 lbs/ft3

Wall Dead load = 150 ( 2 x 1.5 x 10 x ( 30 + 0.75) + ( 20+0.75) ) = 231,750 lbs

78 x 509 x 202 /1000

= 15,881 ft-lb = 191 in-k

Design of Short Span

Assume slab thickness, h = 12 ins.

Mid-span Moment Steel

Steel required for Direct Tension in short span

200b w d 200 (12 x 9.7 )

4/3 of As required by analysis = 4/3 x 0.55 = 0.73 in2

(As = 0.75 in2) steel on top face of slab in short