1

Objective
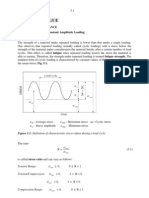
Stress vs
Griffith

Microstructure-Properties: I
Lecture 6B:
Fracture Toughness:
how to use it, and measure it

Plasticity
Plastic
Zone
Example
Measurement
Fractography

27-301
Fall, 2007
Prof. A. D. Rollett

Processing

Performance

MicrostructureProperties

Objective
Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

The objective of this lecture is to build upon

the basic concepts of fracture toughness
and stress intensity introduced in part A.
Realistic approaches to fracture toughness
are considered with information on how to
measure toughness.
Part of the motivation for this lecture is to
prepare the class for a Lab on the sensitivity
of mechanical properties to microstructure.

Key Points
Objective
Stress vs
Griffith

Plasticity
Plastic
Zone

Example
Measurement
Fractography

The Griffith equation applies to technological materials.

Toughness scales with modulus, as does strength.
Toughness is highly dependent on material type: the most
important issue is the presence (toughness) or absence
(brittleness) of plasticity.
Plasticity makes a large contribution to the energy absorbed in
crack propagation because plastic deformation at the crack tip
blunts the tip (lower stress concentration) and substantially
increases the amount of work required per unit crack advance.
Measurement of toughness uses many methods: two basic
methods measure critical stress intensity in plane strain, KIC,
and the energy absorbed in impact (Charpy Test).
Fractography, i.e. classification+quantification of the fracture
surfaces, is useful as a microstructural diagnostic for
toughness, in addition to the quantitative measures of
mechanical behavior.

Toughnesses in Materials

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

Before looking at the influence of microstructure on fracture

toughness, it is useful to review the range of toughnesses
observed in real materials.
We find that to a first (crude!) approximation, toughness
scales with strength.
An immediate refinement is to consider the bonding type in
the various classes of materials: metals tend to have simpler
structures with easier dislocation motion, i.e. more energy
absorbed in crack propagation. Ceramics have covalent or
ionic bonding with much higher resistance to dislocation
motion, especially at ambient conditions.

Map of
toughness vs.
strength

Objective
Stress vs
Griffith

Glass-like
brittleness

Plasticity
Plastic
Zone
Example
Measurement
Fractography

Design with care

below this line!
[Ashby]

Tough

Use of the Griffith equation

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone

Example
Measurement
Fractography

The Griffith equation can be applied immediately to practical

problems.
Problem: estimate the strength of a brittle material (meaning
that we can ignore plastic yield) with properties,
E = 100 GPa, = 1 J.m-2,
2"E
and a crack length of 2.5 m.
! break =
The answer is break = (2E/c) =
#c
(2.1011.1//2.5.10-6)= 160 MPa
Now it is instructive to compare this result with that from the
stress concentration equation, with the crack tip radius set
equal to, say, 8a0:
"E #
break = (E/4a0c) = (E8a0/4a0c) = (2E/c) !
break =
11
-6
(2.10 .1/2.5.10 )= 283 MPa
4a0 c
So, we see that, even for a fairly sharp crack, the Griffith
(energy balance) equation sets the lower limit on fracture
strength.

Which equation controls?

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

Fracture Strength (arbitrary units)

5
Griffith eq.
controls

!fr=!(E"#/4a0c)
(Stress concentration)

!fr=!(2E"/"c)
(Griffith)

2
Stress concentration
equation controls

0
0

5
10
15
Tip Radius (multiples of a0)

20

The paradox: although the Griffith equation (black line) appears to be a

necessary but not sufficient condition for fracture because one also needs for
the stress at the crack tip to exceed the breaking stress (the red line), as a
matter of practical experience, it does successfully predict when fracture will
actually occur.

Application to structural materials

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone

Notwithstanding the previous slides on energy balance

(Griffith) versus stress concentration, the experimental fact is
that the Griffith equation works well for many different
materials.
It works well, not in its literal form with the surface energy
determining the energy consumed, but with an additional
energy term that accounts for the effect of plasticity (crack
bridging, phase transformation.). This was one of Orowans
(many) contributions to the field.

Example
Measurement
Fractography

! break

2(" surface + " plastic)E

=
#c

Toughness

Objective
Stress vs
Griffith
Plasticity

break = Kc/(c)

Plastic
Zone

Fractography

We can also define a toughness, Gc, which is given by

break = (EGc/c)

Example
Measurement

Recall that we define a stress intensity as K=c.

Cracking is defined by K > Kc, where Kc is a critical stress
intensity or fracture toughness, and is a material property.

and allows us to modify (increase) the apparent surface energy

to account for plastic work at the crack tip.
The toughness can be thought of as the combination of
surface energy and plastic work done at the crack tip noted on
the previous slide: Gc = surface + plastic

10

Effect of plasticity
Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

How important is the additional term?

In metals, very important: compared to typical
surface energies between 0.5 and 2 J.m-2, the plastic
work term ranges up to 103 J.m-2. Therefore the
surface energy term can be neglected in most metal
alloys.
Again, we cannot use the Griffith equation in its basic
form, even with the addition of the plastic work,
however.
The plasticity results in a plastic zone immediately in
front of the crack tip. This is the zone within which
significant yielding has occurred. Remember that the
stress concentration leads to locally higher stresses
and so, only in the vicinity of the crack will the yield
stress be exceeded.

11

Plastic Zone

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

The plastic zone is a simple concept to visualize. Within a certain radius of

the crack tip, the yield stress is exceeded
and the material
has deformed
(consuming energy
thereby and
contributing to
toughness). Clearly
the lower the yield
strength, the larger
the plastic zone, rp.
rp
Actually the size
depends on the
ratio of the applied
stress, , to the
yield stress, y :
rp /y
[Dowling]

12

Crack Tip
Objective
Stress vs
Griffith

Different length
scales at which
to view a crack tip

Plasticity
Plastic
Zone
Example
Measurement
Fractography

[McClintock, Argon]

13

Effective crack length

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

An important but slightly counter-intuitive idea is that the effective

crack length is longer than the actual value as a result of the plastic
zone, i.e. ceffective = cactual + rp.
Size of the plastic zone?
rp = K2/202 = 2c/202 2c/22yield.
Substituting this relationship into the standard Griffith equation, we
obtain:
break = Kc/(c),
as
f break = Kc/({c+rp}) = Kc/(c{1 + Kc2/2c02}),
2 {1 + Kc2/2c02} = Kc2/(c),
2 = Kc2(1/(c) - 2 /2c02},
c2 = Kc2(1 - 2 /202),
and re-arrange so that we obtain the following modified form:

0 yield

K effective =

" f #c
2
%
(
1 "
1$ ''
**
2 & " yield )

14

Effective crack length, contd.

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example

This second version is an empirical generalization of the first one: f

is the fracture strength, is the operating stress in the material, and
yield is the yield stress of the material. KIc is the plane strain fracture
toughness (critical stress intensity). A, B and are constants that
depend on crack geometry (of order unity). In the next slides, B is
written as a function of c/a, the ratio of the (elliptical) crack
(semi-)length, a, to its depth, c.
One can either calculate a fracture strength for a given set of
parameters, calculate a maximum operating stress similarly, or,
determine whether the fracture toughness dictated by the quantities
on the RHS is higher than the actual fracture toughness of the
material.

Measurement
Fractography

K Ic =

" f #$c
& " )
B % A((
++
' " yield *

, " f = K Ic

& " )2
B % A((
++
' " yield *
#$c

15

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example

Example
problem

Measurement
Fractography

[Courtney, p431]

16

Measuring Fracture Toughness

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

How do we measure fracture toughness?

Two examples:
A - measure the critical stress intensity (KIc) in plane
strain by measuring the stress required to propagate
a sharp crack.
B - measure the energy absorbed in a rapid fracture
of a bar - the Charpy test.
The first method measures a quantity corresponding
to the values in the equations discussed (but a preexisting crack is used).
The second test is a more macroscopic test but it
includes the effect of crack nucleation (which may be
difficult enough to raise the effective toughness).

17

Compact Tension test

The load is increased until crack propagation starts: for a large enough
specimen, the stress intensity at this point is the critical stress intensity, KIC. P
is the load, t is the specimen thickness, b is the distance from the loading
point to the right-hand face, and Fp is a function of the crack geometry.

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

Fatigue
crack;
grown
before
fracture
expt.

[Dowling]

18

Charpy Test
Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

The Charpy test uses a

square bar with a small
notch in it.
The further the pendulum
swings after breaking the
specimen, the less
energy was absorbed in
the impact, and vice
versa.
Higher toughness results
in higher energy
absorbed.

19

Fractography
Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

Fractography is the practice of characterizing

fracture surfaces.
Surface preparation is not needed - one needs to
examine the surfaces as fractured, which means
that it should be done promptly so as to avoid
changes from oxidation, corrosion etc.
The rough, irregular nature of fracture surfaces
means that optical microscopy is of little use.
Scanning electron microscopy is most useful in
fractography.

20

Sample scale
Example of high strength steel from a compact
tension test.
Objective
Stress vs
Griffith

Crack
propagation

Plasticity
Plastic
Zone
Example
Measurement
Fractography

Shear
Lips
Crack tip

21

Grain scale
Objective

These micrographs contrast the appearance of

ductile and brittle fractures at the microstructural
scale.
[Dowling]

Stress vs
Griffith

Ductile (tearing)

Plasticity
Plastic
Zone
Example
Measurement
Fractography

Brittle (cleavage)

22

Ductile fracture
Cup and cone fracture - each
dimple is a void (which may or
may not have a particle in it)
Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

In contrast to brittle
fracture, which is a
cleavage process
(and, in crystalline
materials typically
follows low index
planes), ductile
fracture only occurs
after much plastic
deformation.

23

Summary (part B)

Objective

Stress vs
Griffith

Plasticity

Plastic
Zone

Example
Measurement
Fractography

The Griffith equation has been extended to technological

materials.
Toughness scales with modulus, as does strength.
Toughness is highly dependent on material type: the most
important issue is the presence (toughness) or absence
(brittleness) of plasticity.
Plasticity makes a large contribution to the energy absorbed in
crack propagation.
Measurement methods contrasted between KIC and impact
testing (Charpy).
Fractography introduced as a diagnostic for toughness, in
addition to the quantitative measures.

24

Case Study:
Failure Analysis of a Rocket Motor Case

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

A rocket motor case was made of a material that had a yield strength of 215 ksi (=
1485 MPa) and a KIC of 53 ksi(in)1/2 (= 58 MPa.m3/2) and it failed at a stress of
150 ksi. Examination of the failed component showed that there was an
elliptical surface crack with a depth of 0.039 inches (= 0.99 mm) and a length
of 1.72 in (= 43.7 mm). Could this flaw have been responsible for the failure?
Answer:
The value of f(c/a) (=B) for this flaw is 1.38. Rearranging the equation that relates
fracture toughness to yield strength and operating stress, we obtain:
2

" fracture =

f (c a ) # 0.212(" " y )
1.20$c

K IC =

1.38 # 0.212(" " y )

1.20$c

K IC

Now we estimate the fracture stress iteratively by substituting values of KIC and
!
the crack depth, c, (not the half-length!) and assume the operating stress
value, , of 150 ksi, in order to estimate the RHS; then we compare the value
on the RHS with the known fracture stress on the LHS. The answer turns out
to be 156 ksi, which is not far off the actual fracture stress of 150 ksi.
Substituting 156 ksi as the operating stress value, , into the RHS produces
156 ksi as the computed fracture stress. At this point the iteration has
converged well enough for our purposes. The close agreement between the
actual and the computed fracture stresses suggests that the flaw was very
likely to have been the cause of the failure.
Source: Courtney: Mechanical Behavior of Materials, Ch. 9.

25

References

Objective
Stress vs
Griffith
Plasticity
Plastic
Zone
Example
Measurement
Fractography

Materials Principles & Practice, Butterworth Heinemann,

Edited by C. Newey & G. Weaver.
G.E. Dieter, Mechanical Metallurgy, McGrawHill, 3rd Ed.
Courtney, T. H. (2000). Mechanical Behavior of Materials.
Boston, McGraw-Hill.
R.W. Hertzberg (1976), Deformation and Fracture Mechanics
of Engineering Materials, Wiley.
N.E. Dowling (1998), Mechanical Behavior of Materials,
Prentice Hall.
D.J. Green (1998). An Introduction to the Mechanical
Properties of Ceramics, Cambridge Univ. Press, NY.
A.H. Cottrell (1964), The Mechanical Properties of Matter,
Wiley, NY.