Professional Documents
Culture Documents
V1i7 Ijertv1is7319 PDF
V1i7 Ijertv1is7319 PDF
Uploaded by
Rolie Sycip M. UyOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
V1i7 Ijertv1is7319 PDF
V1i7 Ijertv1is7319 PDF
Uploaded by
Rolie Sycip M. UyCopyright:
Available Formats
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
Analysis And Design Of R.C. Deep Beams By Finite Strip Method And Comparison
Of Theoretical Results With Experimental Results
Mr. S.S. Patil
Associate Professor, Civil Engineering
Department,
Walchand Institute of Technology.
Solapur India.
Dr. B.R. Niranjan
Professor, Civil Engineering Department.,
U.V.C.E. Bangalore University
Bangalore. India
2.
Abstract
This paper describes analysis and design of deep
beams subjected to two points loading with different
L/D ratios using Programme in FORTRAN 77 for
analysis and codes I.S.456-2000, B.S.8112, ACI 318
and Appendix A of ACI 318 for design purpose, to
plot the variation of flexural stress, strains and shear
stress in deep beam. The parameter, Shear span of
beam was varied during the analysis. Several beams
were cast and tested in laboratory.
Key words: Deep Beam, Finite Strip method, codal
provisions, Design.
1.1.
GENERAL INTRODUCTION
Beams with large depths in relation to spans are
called deep beams10. In IS-456 (2000) Clause 29, a
simply supported beam is classified as
deep when the ratio of its effective span L to overall
depth D is less than 2. Continuous beams are
considered as deep when the ratio
L/D is less than 2.5. The effective span is defined as
the centre-to-centre distance
between the supports or 1.15 times the clear span
whichever is less13.
1.2 OBJECTIVE OF STUDIES:
The main objective of this investigation is to conduct
an experimental study on strength &
behavior of deep beams. The detailed analysis has
been carried out using the finite strip method. The
study also aimed at testing validity & usefulness of IS
456:2000, B.S.8112, ACI 318-2005 and ACI
Appendix A (STM), Draft Eurocode & CEB- FIP
code and Canadian code.
The objectives of the experimental investigation
can be listed as follows.
1. To observe & explain the deflection, cracking &
failure modes of deep beams subjected to two
points loading.
To compare the flexural steel requirement as per
codal provisions with that calculated using the
finite strip method.
3. To comment on suitability of finite strip method
& codal provisions
2. ANALYSIS OF DEEP BEAM
2.1. FINITE STRIP METHOD
The finite strip approach was first introduced by
CHEUNG (1968). For a structure with constant cross
section and end boundary conditions that do not
change transversely, stress analysis can be performed
using finite strips. It is recognized as best method of
analysis for simply supported rectangular plate, deep
beam and box structure in terms of accuracy and
efficiency. Basically, the method is a hybrid
procedure which retains advantages of both the
orthotropic plate Method and finite element concept.
2.2 THE COMPUTER PROGRAM
2.2.1 Introduction: A computer program has been
prepared for the analysis of Deep Beam having
simple support. A computer programme is necessary
for the solution of Equations. It should be noted that
the overall stiffness matrix is symmetrical. Computer
programme is developed on the basis of direct
stiffness method.
The essential steps in writing a programme are as
follows.
1) Presenting input data to computer
2) Evaluation of stiffness matrix of individual strips.
3) Assembling of structure stiffness matrix
4) Forming the load vector
5) Solving the assembled equations for the
displacements.
6) Computing the internal forces in the members and
reactive forces at the support.
7) Presentation of the results.
Features of the Program
1. The programming language used is FORTRAN77.
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
2. The program can handle any number of joints and
members depending upon memory
allocations
available with PC.
3. The program can handle yielding of the support in
all three directions. Also it can handle symmetric
structures in-plane, point load loads etc.
3. VARIATION OF FLEXURAL
STRAIN:
The parametric study to know strain distribution in
case of deep beam is performed here. It is found that
the smaller the span/depth ratio (i.e., less than 2.0),
the more pronounced the deviation of the strain
pattern from that of Euler Bernoulli theory12. Figure 1
& Figure 2 shows that the flexural strain at mid span
of simply supported deep beam for two different
shear span to-depth ratios. The beams have
disturbed region in flexural strain distribution. Deep
beams behave differently from shallow beams. In
these members, the distribution of strain across the
depth of the cross section is nonlinear and a
significant amount of load is carried to the supports
by a compression strut joining the load and the
reaction. These structural elements belong to D
(disturbed) regions. Structural members can be
broadly divided into two regions, namely, B (or
Bernoulli) regions where the strain distributions are
linear, and D (or Disturbed) regions where the strain
distributions are nonlinear. While well defined
theories are available for designing B regions, thumb
rule or empirical equations are still being used to
design D regions, though B and D regions are equally
important. Schlaich et al. (1987) identified deep
beams as discontinuity regions where the strain
distribution is significantly nonlinear and specific
strut-and-tie models need to be developed, whereas
shallow beams are characterized by linear strain
distribution and most of the applied load is
transferred through a fairly uniform diagonal
compression field.
Figure 1 Flexural Strain Distribution shear spanto-depth ratio 0.57
Figure 2 Flexural Strain Distribution shear spanto-depth ratio 0.71
From the variation of flexural strain graphs the
definition of simply supported deep beam as per IS
456:2000 i.e. L/D ratio is less than or equal to 2.0 is
reasonably accurate.
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
4 VARIATION OF FLEXURAL STRESS:
The stresses in isotropic homogeneous deep beams
can be determined using finite strip analysis. It is
found that the smaller the span/depth ratio (i.e., less
than 2.0), the more pronounced the deviation of the
stress pattern from that of Euler Bernoulli theory.
Figure 3 & Figure 4 shows the flexural stress at mid
span of simply supported deep beam for two different
shear span to-depth ratios. The tensile stresses
increase rapidly at the bottom and neutral axis moves
towards soffit of the beam11.
From the variation of flexural stress graphs the
definition of simply supported deep beam as per IS
456:2000 i.e. when L/D ratio is less than or equal to
2.0 is reasonably accurate.
5 VARIATION OF SHEAR STRESS:
Figure 5 & Figure 6 shows the shear stress near
support of simply supported deep beam for two
different shear span to-depth ratios .The beams have
drastic change in shear stress distribution. Deep
beams behave differently from shallow beams. The
shear stress patterns have also changed in case of
deep beam. It is found that the smaller the span/depth
ratio (i.e., less than2.0), the more pronounced the
deviation of the shear stress distribution from that of
Euler Bernoulli theory12.
Figure 3 Flexural Stress Distribution shear spanto-depth ratio 0.57
Figure 5 Shear Stress Distribution shear span-todepth ratio 0.57
Figure 4 Flexural Stress Distribution shear spanto-depth ratio 0.71
Figure 6 Shear Stress Distribution shear span-todepth ratio 0.71
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
From the variation of shear stress graph it is clear that
shear effect is predominant in beams having L/D
ratio less than or equal to 2.0 which may lead to
warping of the section.
6. TENSION REINFORCEMENT
CALCULATIONS FROM GRAPH:
= 4.58062 x 31.819 x 150
0.87 x 415
= 60.55 mm2
Similarly calculations for all the strips are done and
tabulated.
Tension Reinforcement required is calculated from
the flexural stress graphs which are plotted by using
Finite Strip program.
Table 2: Reinforcement required as per FSM for
Shear span 250 mm:
Reinforcement required for Shear span 200 mm:
Sr.No.
Sample calculation of reinforcement for bottom most
strip
Area of steel required =
Flexural stress in strip x Area of Strip
Design stress in steel
1.
2.
3.
4.
5.
6.
= y x Astrip
0.87 fy
= 4.10687 x 31.819 x 150
0.87 x 415
= 54.29 mm2
Similarly calculations for all the strips are done and
tabulated.
Table 1: Reinforcement required as per FSM for
Shear span 200 mm:
Sr.No.
Strip
No.
1.
1
2.
2
3.
3
4.
4
5.
5
6.
6
Total
Reinforcement required mm2
0.86
8.99
17.3
27.183
38.973
54.293
147.6 mm2
Reinforcement required for Shear span 250 mm:
Sample calculation of reinforcement for bottom most
strip
Area of steel required =
Flexural stress in strip x Area of strip
Design stress in steel
= y x Astrip
0.87 fy
Strip
No.
1
2
3
4
5
6
Total
Reinforcement required mm2
0.96
10.032
19.296
30.32
43.805
60.55
164.97 mm2
7. DESIGN OF DEEP BEAMS3
7.1 INTRODUCTION:
Deep beams are designed for two points loading and
for two shear spans viz. 200 mm and 250 mm. Point
loads of 50 kN are applied on deep beams.
Dimensions of deep beams chosen for design purpose
are,
Length = 700 mm,
Depth = 350 mm,
Thickness = 150 mm
7.2 DESIGN METHODS
Design of deep beams is done by following methods.
1. Design by using I.S.456-2000 method
2. Design by using B.S.8112 method
3. Design by using ACI-318 method
4. Design by using ACI-Appendix A (Strut & Tie)
method
For each method mentioned above, several beams
with 200 mm and 250 mm shear spans are designed
and cast for experimental study.
8. EXPERIMENTAL WORK
8.1 INTRODUCTION:
Deep beams are designed by using I.S.456-2000,
B.S.8112, ACI-318 and ACI-Appendix A (strut &
Tie method) for two points loading and for several
shear spans. Dimensions of Deep beams chosen for
design purpose are,
Length = 700 mm,
Depth = 350 mm,
Thickness = 150 mm
9. Testing in Laboratory and Test Results
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
Image 7 Deep beam testing
Mode of failure was found to be shear with diagonal
tension & can be categorized as given in table.
Image 9 Strut formation in deep beams
Image 8 Diagonal cracking in deep beam
TABLE 3: SAMPLE TEST RESULTS
Loading: Two point loading, each point load of 50 kN (working load)
Beam dimensions: Total Length = 700 mm, Effective Span = 600 mm,
Depth = 350 mm, Thickness = 150 mm, Average cube strength = 21 N/mm 2
Beam No.
B 1/1
B 1/2
B 2/1
B 2/2
B 3/1
B3/2
B 4/1
B 4/2
Design Method
I.S.456
I.S.456
B.S.8112
B.S.8112
ACI 318
ACI 318
Strut
& Tie
Strut
& Tie
200
250
200
250
200
250
200
250
0.57
0.71
0.57
0.71
0.57
0.71
0.57
0.71
Shear span (mm)
Shear span to depth
ratio
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
Reinfor
cement
provide
d
(No.of
bars)
Load at
first
crack
Failure
Load
Deflecti
on at
failure
Flexure
steel
Required
in mm2`
Flexure
steel
Provided
i) 10 mm
ii) 08
mm
iii) mm2
231.33
231.33
169.52
215.89
207.24
207.24
207.24
235.62
235.62
200.96
235.62
126
126
113.04
113.04
282.6
282.6
262.5
262.5
105
105
84.78
84.78
113.04
113.04
72
72
6
2
6
2
4
3
4
3
9
4
9
4
5
3
5
3
200kN
190kN
180kN
170kN
220kN
210kN
210kN
200kN
100kN
95kN
90kN
85kN
110kN
105kN
105kN
100kN
300kN
280kN
285kN
275kN
340kN
334kN
330kN
310kN
150kN
140kN
142.5kN
137.5Kn
170kN
167kN
165kN
155kN
3.4 mm
3.8 mm
3.5 mm
4 mm
3.6 mm
3.75 mm
3.5 mm
3.7 mm
Permissi
ble
deflectio
n
2.4 mm
2.4 mm
2.4 mm
2.4 mm
2.4 mm
2.4 mm
2.4 mm
2.4 mm
Deflectio
n at 150
kN load
1.03 mm
1.37 mm
1.24 mm
0.9 mm
1.10 mm
1.26 mm
1.33
mm
1.52 mm
Mode
II- 3
Mode
II- 3
Mode
II- 3
Mode
II- 3
Mode
II- 3
Mode
II- 3
Mode
II- 3
Mode
II- 3
Shear
Required
in mm2`
Vertical
Horizont
al
6 mm
dia.
Vertical
Horizont
al
Total
Each
Point
load
Total
Each
Point
load
Total
Observed mode of
failure
160.74
199.845
160.74
207.24
199.85
Referring to table nos. 1, 2 and 3, it is found that
flexural steel reinforcement as per FINITE STRIP
METHOD is less than that specified by codes.
Description of modes of failure as described by
Salamy et al8:
Failure modes of deep beam can be divided in
following two main categories.
a.
Flexural failure mode
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
b.
Shear failure mode
Shear failure mode can be sub divided into following
three categories.
Mode II-1: Diagonal tension failure, which in the
line of thrust become so eccentric and give rise to
flexural failure in compressive zone. It is important
however to mention that this kind of failure is a result
of tensile crack extension in compressive zone due to
flexural load8.
Mode II-2: Shear compression failure where RC
beam fails due to the development of diagonal crack
into the compressive zone and reduces the area of
resisting region excessively and beam crushes once
generated compressive stress exceeds compressive
strength of concrete8.
Mode II-3: Shear proper or compressive failure of
struts, which is often observed in beams with very
small shear span to depth ratio
(a/d < 1.5).In this
case due to the small a/d ratio, the line of thrust will
be so steep and arch action not
only reserve flexural capacity in most cases but also
efficiently sustains required shear force. Arch is
clearly observed in those beams and finally beams
fail due to either sudden tensile crack formation
parallel to the strut axes or compressive crush in
normal
direction
to
the
strut
axes8.
Fig. 10 GRAPHS OF LOAD VS DEFLECTION
10. CONCLUSION
1.
2.
3.
Following conclusions can be drawn from above
studies.
Failure of deep beams was mainly due to diagonal
cracking and it was along the lines joining the
loading points and supports.
The strength of beams with 250 mm shear span is
about 5 % less than that of 200 mm shear span. It is
clear from these results that the strength of deep
beam is inversely proportional to the shear span for
the constant depth of the beam.
No separate checking for shear is specified in I.S.456.
It is assumed that the arching action of the main
tension steel & the web steel together with concrete
will carry the shear.
4. All the beams had low deflection at failure as there
was no flexural failure.
5. The overall average load at first crack was found
approximately half of the ultimate failure load.
Therefore in design of deep beams, a load factor of
1.5 seems to be reasonable. As reported by F.K.Kong
the shear strength of deep beams is 2 to 3 times
greater than that given by usual equations which is
true as in our case the strength is about 2 times
greater than design loads.
6. Strut-and-tie model is a good approach to design. It is
a simple approach but provisions against web
cracking are not clearly given in this method. Though
it is a conservative method, the area of steel
calculated using the STM is nearly equal to that
required as per IS456:2000, BS8112-2006 and
ACI318-05 codal recommendations.
7. The flexural steel requirement of IS456:2000 & BS
8112-2006 methods are more by a margin of 8.17 %
than Finite Strip Method whereas in case of STM
method this margin is found to be 12.93 %. But in
case of ACI-318 method it is 36.19 % more than
FSM method. Therefore it can be concluded that
tensile reinforcement requirements of I.S., B.S. &
STM methods are near to the FSM whereas the same
by ACI -318 methods is
more. Therefore the
strength of beams designed by ACI -318 method is
about 10 % more than other beams.
8. Web steel requirement of ACI-318 method is more
than other methods due to specification of minimum
spacing of d/5. Due to more web steel, initial
cracking load of the beams designed by ACI-318
method is about 7 % more than that of the beams
designed by other methods. Even if web
reinforcement does not contribute substantially to the
strength of deep beams, it prevents initial cracking of
loads at low loads.
9. B.S. 8112 takes into account the contribution of
horizontal web steel also along with vertical steel.
This reduces the vertical steel requirement. The
design was found conservative.
10. The flexural tensile force as per the FSM analysis
is concentrated in lower 1/3 height for all the
beams. Therefore in the deep beams loaded with
two point loading, steel for the flexural tensile
force may be provided mainly in this height. This
is matching with all the codal provisions.
11. REFERENCES
1. Varghese, and Krishnamurthy, Strength and
Behavior of Deep Reinforced Concrete Beams
Indian Concrete Journal, March 1966,pp 104108,
www.ijert.org
International Journal of Engineering Research & Technology (IJERT)
ISSN: 2278-0181
Vol. 1 Issue 7, September - 2012
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
Peter Marti, Basic Tools of Reinforced Concrete
Beam Design ACI journal, January-February
1985, Title No. 82-4.
Mr.Kotsovos, Design of Reinforced Concrete
Deep Beams Journal of Structural Engg.,
January 1988, pp 28-32.
Matamoros, and Wong, Design of Simply
Supported Deep Beam using strut and tie
models ACI Structural journal, November/
December 2003, Title No.100-S72.
Quintero-Febres, Parra-Montesinos, and Wight,
Strength of Struts in Deep Concrete Members
using Strut and Tie Method, ACI Structural
journal, July/ August 2006,Title No. 103-S61.
David M. Rogowsky, James G. MacGregor, and
See Y. Ong, Tests of Reinforced Concrete Deep
Beam, ACI Journal, July-August1986, pp 614623.
P Nagarajan, Dr T M M Pillai, and Dr N
Ganesan, Design of simply supported Deep
Beam using IS 456: 2000 and Strut and Tie
Method, IE (I) Journal-CV, Vol.88, May 2007.
Pp 38-43,
Mohammed Reza Salamy. Hiroshi Kobayashi
and Shigeki Unjoh. Experimental and
Analytical Study on Deep Beams
Design by Strut and Tie method using ACI
Appendix A from STM website.
P.C. Varghese Advanced Reinforced Concrete
Design, Prentice Hall of India Pvt.Ltd. New
Delhi.
F. K. Kong. Reinforced Concrete Deep Beam,
Van Nostrand Reinhold, New York
R Park and T Pauly. Reinforced Concrete
Structure', Wiely-Interscience Publications.
Indian Standard Code of Practice Plain and
Reinforced Concrete IS 456:2000-. Bureau of
Indian Standards, Manak Bhavan, New Delhi,
India.
ACI 318-05. Building Code Requirements for
Structural
Concrete
and
Commentar.
American Concrete Institute, Detroit, USA.
www.ijert.org
You might also like
- Member Stiffness and Contact Pressure Distribution of Bolted JointsDocument8 pagesMember Stiffness and Contact Pressure Distribution of Bolted JointsreaderScribd9100% (1)
- Ilovepdf Merged PDFDocument784 pagesIlovepdf Merged PDFRe DesignNo ratings yet
- Amharic Language ManualDocument15 pagesAmharic Language ManualVishnu Samy50% (2)
- 1 Wall Floor TilesDocument68 pages1 Wall Floor TilesRaymond Chan100% (2)
- Electrodeposited Copper For Engineering UsesDocument4 pagesElectrodeposited Copper For Engineering UsesVatsalNo ratings yet
- Gusset Plate Stability Using Variable Stress TrajectoriesDocument6 pagesGusset Plate Stability Using Variable Stress TrajectoriestmaNo ratings yet
- Stiffened Plates PDFDocument16 pagesStiffened Plates PDFfarhadmrt6923No ratings yet
- Design With Strut and Tie Models ES en 2015 Training - MoCDocument38 pagesDesign With Strut and Tie Models ES en 2015 Training - MoCAbdifatah HassanNo ratings yet
- Sir AquinoDocument529 pagesSir AquinoJat Bacsafra0% (2)
- Anchor Grout DesignDocument129 pagesAnchor Grout DesignNil DG100% (1)
- Punching of Concrete Slabs Without Shear Reinforcement - GuandaliniDocument9 pagesPunching of Concrete Slabs Without Shear Reinforcement - GuandaliniAnonymous YAHRBwSYnNo ratings yet
- Steel Structures Tension Members 2Document24 pagesSteel Structures Tension Members 2Nafi AykutNo ratings yet
- AB31GDocument9 pagesAB31GDiego Alexander BNo ratings yet
- Effects of Opening On The Behavior of Reinforced Concrete Beam I011275261Document10 pagesEffects of Opening On The Behavior of Reinforced Concrete Beam I01127526101010No ratings yet
- Geo 249 PDFDocument60 pagesGeo 249 PDFリムスィギャン瑞娴No ratings yet
- Mathcad-Cross-Section RESISTANCE Under Bending and CompressionDocument5 pagesMathcad-Cross-Section RESISTANCE Under Bending and CompressionValentinNo ratings yet
- Design of Large Footings For One Way ShearDocument8 pagesDesign of Large Footings For One Way ShearAsad SohailNo ratings yet
- Skempto 1961 Effective Stress in Soils Concrete and RocksDocument13 pagesSkempto 1961 Effective Stress in Soils Concrete and RocksSaid_Lopez_Mx100% (1)
- Esteem 8 Technical Documentation PDFDocument860 pagesEsteem 8 Technical Documentation PDFLau Kim Hwa80% (5)
- Analysis of Cylindrical Shell Structure With Varying Parameters PDFDocument6 pagesAnalysis of Cylindrical Shell Structure With Varying Parameters PDFesatjournalsNo ratings yet
- Comparison of One-And Two-Way Slab Minimum Thickness Provisions in Building Codes and StandardsDocument7 pagesComparison of One-And Two-Way Slab Minimum Thickness Provisions in Building Codes and StandardsM Refaat FathNo ratings yet
- Engineering Vibroacoustic Analysis: Methods and ApplicationsFrom EverandEngineering Vibroacoustic Analysis: Methods and ApplicationsStephen A. HambricNo ratings yet
- Analysis of R.C Deep Beam by Finite Element Method: B.R. Niranjan, S.S.PatilDocument4 pagesAnalysis of R.C Deep Beam by Finite Element Method: B.R. Niranjan, S.S.PatilIJMERNo ratings yet
- Non Linear Finite Element Method of Analysis of Reinforced Concrete Deep BeamDocument7 pagesNon Linear Finite Element Method of Analysis of Reinforced Concrete Deep BeamIJMERNo ratings yet
- Strut-And-Tie Model Design Provisions: Robin G. Tuchscherer, David B. Birrcher, and Oguzhan BayrakDocument16 pagesStrut-And-Tie Model Design Provisions: Robin G. Tuchscherer, David B. Birrcher, and Oguzhan BayrakDavid Apaza QuispeNo ratings yet
- Multi-Axial Fatigue Life Prediction of Bellow Expansion JointDocument8 pagesMulti-Axial Fatigue Life Prediction of Bellow Expansion JointedmondNo ratings yet
- Experimental Stress Analysis (Meen 405) : Strain Gages (Electrical Resistance Strain Gages)Document8 pagesExperimental Stress Analysis (Meen 405) : Strain Gages (Electrical Resistance Strain Gages)CalipherhNo ratings yet
- Development of Strut and Tie Models For Simply Supported Deep Beams Using Topology OptimizationDocument7 pagesDevelopment of Strut and Tie Models For Simply Supported Deep Beams Using Topology OptimizationzxcvhjNo ratings yet
- TTM PDFDocument9 pagesTTM PDFAlemie ShitaNo ratings yet
- IJASC5 Post PrintDocument30 pagesIJASC5 Post PrintHuy NguyenNo ratings yet
- Analysis and Design of Simply Supported Deep Beams Using Strut and Tie MethodDocument10 pagesAnalysis and Design of Simply Supported Deep Beams Using Strut and Tie MethodBrandon LevineNo ratings yet
- ResDocument3 pagesRes245120736081No ratings yet
- Comparison of Experimental Strength of R PDFDocument5 pagesComparison of Experimental Strength of R PDFPiyush PrajapatiNo ratings yet
- Characteristic Withdrawal Capacity and Stiffness of Threaded RodsDocument13 pagesCharacteristic Withdrawal Capacity and Stiffness of Threaded RodsAndrej SørensenNo ratings yet
- Analysis of Expansion Joint - A Case StudyDocument9 pagesAnalysis of Expansion Joint - A Case StudyIJRASETPublicationsNo ratings yet
- Cib8138 PDFDocument6 pagesCib8138 PDFChee Fong MakeNo ratings yet
- Comparison of Analysis of Folded Plate Structures by Simplified Bending Theory and Ansys ProgramDocument8 pagesComparison of Analysis of Folded Plate Structures by Simplified Bending Theory and Ansys Programimad rashidNo ratings yet
- 3 Analysis of Deep Beam Using Cast SoftwareDocument7 pages3 Analysis of Deep Beam Using Cast SoftwareSameer Ul BashirNo ratings yet
- SSRN Id4163209Document7 pagesSSRN Id4163209Deepak KumarNo ratings yet
- Study of Interfacial Pressure Distribution For Preloaded Bolted ConnectionDocument6 pagesStudy of Interfacial Pressure Distribution For Preloaded Bolted ConnectionRohit JayashreeNo ratings yet
- Analysis and Design of Members For TensionDocument84 pagesAnalysis and Design of Members For TensionicpertacortaNo ratings yet
- Analysis and Design of Members For TensionDocument91 pagesAnalysis and Design of Members For TensionAL DANIEL VIN FULVADORANo ratings yet
- Frequency Response of Thin Film Chip ResistorsDocument4 pagesFrequency Response of Thin Film Chip Resistorsaarumugam_rajendranNo ratings yet
- Effective Flange Width For Composite Steel BeamsDocument16 pagesEffective Flange Width For Composite Steel Beamspolash72No ratings yet
- 079180285X PipeStressEngineeringDocument5 pages079180285X PipeStressEngineeringJAVIER RICARDONo ratings yet
- Broadside CouplerDocument6 pagesBroadside CouplerBen WalpoleNo ratings yet
- 01 Olleak Egypt JapanUnivofScienceandTechnology PDocument8 pages01 Olleak Egypt JapanUnivofScienceandTechnology PaykutartacNo ratings yet
- Beam-To-Beam Joints With Bolted End-Plate Connections Concerning Steel Platforms Angra 2 NPPDocument10 pagesBeam-To-Beam Joints With Bolted End-Plate Connections Concerning Steel Platforms Angra 2 NPPihpeterNo ratings yet
- Strain Gauges NptelDocument15 pagesStrain Gauges Nptelsushant271992No ratings yet
- (2008) Chan and Gradner EHSDocument11 pages(2008) Chan and Gradner EHSRaees MazharNo ratings yet
- CIVE 302 - Lab 1 - Tensile Testing of Steel PDFDocument9 pagesCIVE 302 - Lab 1 - Tensile Testing of Steel PDFAhmadAliAKbarPhambraNo ratings yet
- Lab ManualDocument14 pagesLab ManualBenni AmirNo ratings yet
- Sp208-04ex 6Document22 pagesSp208-04ex 6Žarko LazićNo ratings yet
- Cosmos Design Star Study - The Tensile Test of The Rectangular PlateDocument12 pagesCosmos Design Star Study - The Tensile Test of The Rectangular PlateapsarasoNo ratings yet
- 2002 - Shear Lag in Double Angle Truss ConnectionsDocument8 pages2002 - Shear Lag in Double Angle Truss ConnectionsPO AsselinNo ratings yet
- 221 Lab 1 - Tensile Testing of Metals (2017W)Document8 pages221 Lab 1 - Tensile Testing of Metals (2017W)Abdul HafieNo ratings yet
- Ultimate Shear Strength of Fibrous Moderate Deep Beams Without StirrupsDocument6 pagesUltimate Shear Strength of Fibrous Moderate Deep Beams Without StirrupsIJERDNo ratings yet
- School of Civil Engineering Sydney NSW 2006 Australia: Shear Buckling of Thin-Walled Channel SectionsDocument22 pagesSchool of Civil Engineering Sydney NSW 2006 Australia: Shear Buckling of Thin-Walled Channel SectionsDadir AliNo ratings yet
- Module B: Tension MembersDocument21 pagesModule B: Tension MembersFerdz PequiroNo ratings yet
- Effects of Creep and Shrinkage On The DeflectionDocument17 pagesEffects of Creep and Shrinkage On The Deflectionabubakrahmed083No ratings yet
- Design of Compression Members Based On IS 800-2007 AND IS 800-1984-COMPARISONDocument5 pagesDesign of Compression Members Based On IS 800-2007 AND IS 800-1984-COMPARISONHeather CarterNo ratings yet
- Welcome To 2008 SDPWS Diaphragm Deflection DesignDocument45 pagesWelcome To 2008 SDPWS Diaphragm Deflection DesignSaeed HassaniNo ratings yet
- Design of Rounded Dovetail JointsDocument6 pagesDesign of Rounded Dovetail JointsJerry ZhangNo ratings yet
- Stco 201310014Document10 pagesStco 201310014DamirNo ratings yet
- Photoelastic and Numerical Analysis of A Sphere/plan Contact ProblemDocument7 pagesPhotoelastic and Numerical Analysis of A Sphere/plan Contact ProblemfjNo ratings yet
- The Fatigue Strength of Transverse Fillet Welded Joints: A Study of the Influence of Joint GeometryFrom EverandThe Fatigue Strength of Transverse Fillet Welded Joints: A Study of the Influence of Joint GeometryNo ratings yet
- Integrated Imaging of the Earth: Theory and ApplicationsFrom EverandIntegrated Imaging of the Earth: Theory and ApplicationsMax MoorkampNo ratings yet
- Iphone Ringtone: Ca#Gc Fca#Cf Gga#Cca#Gcfca#Cf Gga#Cca#Gcfca#Cf Gga#Cca#Gcfca#CfDocument1 pageIphone Ringtone: Ca#Gc Fca#Cf Gga#Cca#Gcfca#Cf Gga#Cca#Gcfca#Cf Gga#Cca#Gcfca#CfVishnu SamyNo ratings yet
- Tablature For Ilayanila - Guitar Tabs and NotesDocument2 pagesTablature For Ilayanila - Guitar Tabs and NotesVishnu SamyNo ratings yet
- Ilaya Nila - Page 3 - WholeNote Guitar LessonDocument3 pagesIlaya Nila - Page 3 - WholeNote Guitar LessonVishnu SamyNo ratings yet
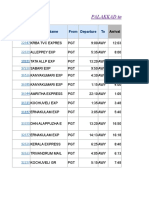
- Palakkad To Aluva Train ScheduleDocument3 pagesPalakkad To Aluva Train ScheduleVishnu SamyNo ratings yet
- Gmail - Your IndiGo Itinerary - M6THHV - Chennai CoimbatoreDocument3 pagesGmail - Your IndiGo Itinerary - M6THHV - Chennai CoimbatoreVishnu SamyNo ratings yet
- Analysis and Design of Multistory Building With Grid Slab Using ETABSDocument12 pagesAnalysis and Design of Multistory Building With Grid Slab Using ETABSVishnu SamyNo ratings yet
- Asking and Giving Directions Conversation English LessonDocument2 pagesAsking and Giving Directions Conversation English LessonVishnu SamyNo ratings yet
- Choose An Outbound Flight: FlightsDocument1 pageChoose An Outbound Flight: FlightsVishnu SamyNo ratings yet
- Booking A Taxi Conversation at A HotelDocument2 pagesBooking A Taxi Conversation at A HotelVishnu SamyNo ratings yet
- Al Musanna College of Technology: Academic Year: 2016 - 2017 (Semester 1 - 01-SEP-16) Attendance SheetDocument3 pagesAl Musanna College of Technology: Academic Year: 2016 - 2017 (Semester 1 - 01-SEP-16) Attendance SheetVishnu SamyNo ratings yet
- Al Musanna College of Technology: Academic Year: 2016 - 2017 (Semester 1 - 01-SEP-16) Attendance SheetDocument3 pagesAl Musanna College of Technology: Academic Year: 2016 - 2017 (Semester 1 - 01-SEP-16) Attendance SheetVishnu SamyNo ratings yet
- Al Musanna College of Technology: Academic Year: 2016 - 2017 (Semester 1 - 01-SEP-16) Attendance SheetDocument2 pagesAl Musanna College of Technology: Academic Year: 2016 - 2017 (Semester 1 - 01-SEP-16) Attendance SheetVishnu SamyNo ratings yet
- Chennai Places To VisitDocument1 pageChennai Places To VisitVishnu SamyNo ratings yet
- Gerd DietDocument2 pagesGerd DietVishnu SamyNo ratings yet
- (Established Under Section 3 of The UGC Act 1956) : Reg. No (12PBECE601)Document1 page(Established Under Section 3 of The UGC Act 1956) : Reg. No (12PBECE601)Vishnu SamyNo ratings yet
- ConcepteursDocument1 pageConcepteursVishnu SamyNo ratings yet
- FAQs For Family LawDocument9 pagesFAQs For Family LawVishnu SamyNo ratings yet
- Stores LocatorDocument1 pageStores LocatorVishnu SamyNo ratings yet
- Karpagam University: Faculty of EngineeringDocument1 pageKarpagam University: Faculty of EngineeringVishnu SamyNo ratings yet
- Zhu Dongqis Thesis PDFDocument188 pagesZhu Dongqis Thesis PDFThomas FritzNo ratings yet
- QTM-Pressure Operations ManualDocument68 pagesQTM-Pressure Operations ManualRizwan FaridNo ratings yet
- Implantes SubperiosticosDocument8 pagesImplantes SubperiosticosJondalys LópezNo ratings yet
- Industry Binder FOAMGLAS Products, Insulation Systems, Accessories Products.Document188 pagesIndustry Binder FOAMGLAS Products, Insulation Systems, Accessories Products.Christian DoriaNo ratings yet
- Structural Maintenance of Dockside Container Cranes 2008 PDFDocument35 pagesStructural Maintenance of Dockside Container Cranes 2008 PDFMajdi JerbiNo ratings yet
- Study of Stress Strain Curve and Moment of Resisitance For Lightweight ConcreteDocument19 pagesStudy of Stress Strain Curve and Moment of Resisitance For Lightweight ConcreteJitendra YadavNo ratings yet
- ASMEPVP2018-84458-Final (Dragged) 2Document1 pageASMEPVP2018-84458-Final (Dragged) 2dowload_bearliaNo ratings yet
- Modeling The ARL 14.5 MM BS41 Surrogate Projectile For Ballistic Impact ComputationsDocument16 pagesModeling The ARL 14.5 MM BS41 Surrogate Projectile For Ballistic Impact Computationscauchyjohn0No ratings yet
- Introduction Compression TestDocument7 pagesIntroduction Compression TestEr Dinesh TambeNo ratings yet
- SSDD Lecture Notes A60130 Image Marked TextmarkDocument51 pagesSSDD Lecture Notes A60130 Image Marked TextmarkNikhilesh VarmaNo ratings yet
- KR Standard For FPR Ships 2020 PDFDocument103 pagesKR Standard For FPR Ships 2020 PDFمجتبی فرامرزیNo ratings yet
- Unit 2 Materials TechnologyDocument17 pagesUnit 2 Materials TechnologyМөнх-Оргил Д.No ratings yet
- Reinforced ConcreteDocument18 pagesReinforced ConcreteWei ShenNo ratings yet
- Engineering Geological Properties and Durability Assessment of TheDocument13 pagesEngineering Geological Properties and Durability Assessment of TheXochiquetzalli Ávila LópezNo ratings yet
- PDC Bit DesignDocument5 pagesPDC Bit Designsuresh_501No ratings yet
- Project DataDocument11 pagesProject DataAbdullah NajjarNo ratings yet
- Aramv22 N1 P1 12Document12 pagesAramv22 N1 P1 12hamedpdmsNo ratings yet
- DME-Module 2-Ktunotes - inDocument45 pagesDME-Module 2-Ktunotes - inme.nithinchandranNo ratings yet
- Elasticity: Engineering Physics Materials by Praveen N. Vaidya, SDMCET, DharwadDocument9 pagesElasticity: Engineering Physics Materials by Praveen N. Vaidya, SDMCET, DharwadpraveenNo ratings yet
- Aluminum Alloy Common Grade 6061 w/T4 TemperDocument7 pagesAluminum Alloy Common Grade 6061 w/T4 TemperPhyo ThuNo ratings yet
- Weldwell Spectrum July Dec 2019Document20 pagesWeldwell Spectrum July Dec 2019Mahesh DeshmukhNo ratings yet