Progression PDF

http://sahatmozac.blogspot.
com
ADDITIONAL MATHEMATICS
FORM 5
MODULE 1
ARITHMETIC PROGRESSION
http://mathsmozac.blogspot.com
http://sahatmozac.blogspot.com
CHAPTER 1: ARITHMETIC PROGRESSION

CONTENTS
PAGE
2
1.1 Identify characteristics of arithmetic progression

1.2
Determine whether a given sequence is an

arithmetic progression
1.3 Determine by using formula:

a) specific terms in arithmetic progressions
b) the number of terms in arithmetic
progressions
1.4
1.5
Find
a) The sum of the first n terms of arithmetic
progressions
b) The sum of a specific number of consecutive
terms of arithmetic progressions
c) The value of n , given the sum of the first n
terms of arithmetic progressions.
Solve problems involving arithmetic progressions
SPM QUESTIONS
4-5
7
8-10
ASSESSMENT
11-12
ANSWERS
13
1
PROGRESSIONS
( Arithmetic Progression)
ARITHMETIC PROGRESSION
The sum of the first n term:
The nth term :

Tn = ___________
Sn = ______________
or
Tn = ___________
Sn = ______________
or
a = _______________
d = _______________
l = _______________
n = _______________
Fill in the blank
1.1 Identify characteristics of arithmetic progression:

EXERCISE 1:
Complete each of the sequence below to form an arithmetic progression.
a) 2, _____ , 8 , ______ , 14 , 17
b) -2 , -5 , ______ , -11 , ________
1
c) -4, ______ , ______ ,
,2
2
d) 2x -3 , 2x -1 , __________ , __________ , 2x + 5
2
1.2 Determine whether a given sequence is an arithmetic progression

EXERCISE 2 :
1. Determine whether a given sequence below is an arithmetic progression.
a) 5 , 11 , 17 , 23 , ..
( ____________________ )
b) -20 , -50 , -30 , -35 , . ( ____________________ )

c) 1 , 4 , 9 , 16 ,
d)
2.
( ____________________ )
2x + y , 4x y , 6x -3y , ( ____________________ )
k +3 , 2k + 6 ,8 are the first three terms of an arithmetic progression,find the

value of k.
Note:
If x,y and z are three terms of
an arithmetic progression ,
yx=z-y
3.
Given that x 2 ,5 x, 7 x 4 are three consecutive terms of an arithmetic progression

W
here x has a positive value. Find the value of x.
4. Given that the first three terms of an arithmetic progression are 2 y,3 y 3 and 5y+1 .
Find the value of y.
3
1.3 Determine by using formula:

a. specific terms in arithmetic progressions
b. the number of terms in arithmetic progressions
Tn a(n1)d
EXERCISE 3:
1. Find the 9th term of the arithmetic
progression.
2, 5 , 8 , ..
Solution:
a=2
d = 5-2=3
2. Find the 11th term of the arithmetic

progression.
5
3, , 2,........
2
T9 2 (9 1)3
= _______
3. For the arithmetic progression
0.7, 2.1 , 3.5, .. ,find the 5th term .
4. Find the nth term of the arithmetic

progression
1
4, 6 , 9,.....
2
5. Find the 7th term of arithmetic

progression k, 2k + 1, 3k+2, 4k+3,.
6. Given that arithmetic progression

9 +6x , 9+4x, 9+2x,
Find the 10th term.
4
EXERCISE 4:
1. Find the number of terms of the

5 , 8 , 11 , . Which term is equal
to 320 ?
a) 4,9.14,.. ,64
Tn 64
4 + (n-1)5=64
4+ 5n-5 =64
5n=65
n= 13
b) -2, -7, -12, , -127
3. The sequence 121 , 116 , 111 , . is

an arithmetic progression. Find the
first negative term in the progression.
1 1
1
c) 1,1 ,1 ,......, 4
6 3
2
d) x y, x y, x 3 y,........., x 31y
4. Find the number of terms of the

a 2b,3a 3b,5a 4b,......, 23a 13b
5
1.4 Find
a) the sum of the first n terms of arithmetic progressions.
b) the sum of a specific number of consecutive terms of arithmetic
progressions.
c) the value of n , given the sum of the first n terms of arithmetic
progressions.
n
2 a n 1 d
2
n
Sn =
a + l
2
l = t h e n th t e r m
S
or
EXERCISE 5:
1. Find the sum of the first 12 terms of
the arithmetic progression
-10 , -7 , -4,

-4 , 1 , 6 , .find the sum of all
the terms from the 6th term to the 14th
term.
2. Find the sum of all the terms of the

38 , 31 , 24 , ., -18
How many terms of the arithmetic

2, 8 , 13 ,18 , must be taken
for the sum to be equal to 1575?
Solution:
Sum of all the terms from the 6th term
to the 14th
= S14 S5
=
=
6
1.5 Solve problems involving arithmetic progressions.

EXERCISE 6:
1. The 5th and 9th of arithmetic
progression are 4 and 16 respectively.
Find the 15th term.
Solution:
T5 4
a (5 1)d 4
a 4d 4 ......(1)
T9 16
The 2nd and 8th terms of an arithmetic

progression are -9 and 3 respectively.
Find
a) the first term and the comman
difference.
b) the sum of 10 terms beginning from
the 12th term.
2.
a+(9-1)d=16
a+8d=16 ......(2)
Solve simultaneous equation to find
the value of a and d, then the 15th term.
3.
The sum of the first 6 terms of an

arithmetic progression is 39 and the
sum of the next 6 terms is -69. Find
a) the first term and the common
difference
b) the sum of all the terms from the
15th term to the 25th term.
4. The sum of the first n terms is given

by S n 6n 2 3n
Find
a) the nth term in terms of n
b) the common difference
7
SPM QUESTIONS:
1. 2003:
Paper 1: (no. 7)
The first three terms of an arithmetic progression are k 3, k 3, 2k 2
Find
a) the value of k
b) the sum of the first 9 terms of the progression
3 marks
2. 2004:
Paper 1: ( no 10)
Given an arithmetic progression -7, -3, 1, . , state three consecutive terms in this
progression which sum up to 75
3 marks
8
3. Paper 1: ( no. 11)

The volume of water in a tank is 450 litres on the first day. Subsequently, 10 litres of
water is added to the tank everyday.
Calculate the volume , in litres , of water in the tank at the end of the 7th day.
2 marks
4. 2005:
Paper 1: (no. 11)
The first three terms of an arithmetic progression are 5, 9, 13
Find
a) the common difference of the progression
b) the sum of the first 20 terms after the 3rd term.
9
4 marks
5. Paper 2 : ( Section A no.3)

Diagram 1 shows part of an arrangement of bricks of equal size.
Diagram 1
The number of bricks in the lowest row is 100. For each of the rows, the number of
bricks is 2 less than in the row below. The height of each bricks is 6 cm.
Ali builds a wall by arranging bricks in this way. The number of bricks in the highest
row is 4. Calculate
a) the height , in cm, of the wall
[ 3 marks ]
b) the total price of the bricks used if the price of one brick is 40 sen. [ 3 marks ]
10
ASSESSMENT:
1. The sequence -13,-10,-7,,128,131 is an arithmetic progression. Find
a) the number of terms in the progression
b) the sum of all the terms in the progression.
2.
3.
Given that k-1 , 2k 4 and k +5 are the first three terms of arithmetic progression.
Find the common difference.
Calculate how many months it will take to repay a debt of RM5800 by monthly
payment of RM100 initially with an increase of RM20 for each month after that.
11
4. The 4th of an arithmetic progression is 18 and the sum of the first eight terms
of the progression is 124. Find
a) the first term and the common difference
b) the sum of all the terms from the 10th term to the 20th term.
5.
Sum of the first ten of the arithmetic progression is 230 and sum of ten terms
after that is 830. Find the first term and the common difference.
12
ANSWERS:
EXERCISE 1:
a) 5,11
b) -8,-14
1
c) 2 , 1
2
d) 2x+1,2x+3
EXERCISE 3:
1. 26
2. -2
3. 6.3
1
4. Tn 5n 3
2
5. 7k+6
6. T10 9 12 x
EXERCISE 5:
1.
2.
3.
4.
78
90
369
40
ASSESSMENT:
1. a) 49
b) 2891
2. 3
3. 20
4. a) 33,-5
b) -407
5. 4,6
EXERCISE 2:
1. a) Arithmetic progression
b) Not an arithmetic progression
c) Not an arithmetic progression
d) Arithmetic progression
1
2. k
3
3. x = 4
4. y = 5
EXERCISE 4:
1. a) 13
b) 26
c) 22
d) 45
2. T106
3. T26 4
4. 12
EXERCISE 6:
1. 34
2. a) -11,2
b) 200
3. a) a=14 , d= -3
b) -473
4. a) Tn=12n-3
b) d=12
PAST YEAR QUESTION:
1. a) k=7
b) S9 252
2. T10 29, T9 25, T8 21
3. T7 510
4. a) 4
b) 1100
5. a) 294
b) RM1019.20
13
ADDITIONAL MATHEMATICS
FORM 5
MODULE 2
PROGRESSIONS
(Geometric Progression)
14
CHAPTER 2 : GEOMETRIC PROGRESSIONS

Contents
Page
2.1
CONCEPT MAP (GEOMETRIC PROGRESSIONS)
2.2
IDENTIFY CHARACTERISTICS OF GEOMETRIC

PROGRESSIONS
2.3
DETERMINE WHETHER A GIVEN SEQUENCE IS A

GEOMETRIC PROGRESSION
2.4
DETERMINE BY USING FORMULA
a) specific terms in geometric progressions

b) The number of terms in geometric progressions
2.5
FIND
6
a) The sum of the first n terms of of geometric
Progressions
b) The sum of a specific number of consecutive terms
of geometric Progressions
c) The value of n ,given the sum of the first n terms
of geometric Progressions
2.6
FIND
a) The sum to infinty of geometric progressions
b) The first term or common ratio, given the sum to
infinity
2.7 SOLVE PROBLEMS INVOLING GEOMETRIC

PROGRESSIONS
SPM Questions
11
14
15
15
Assessment test
18
Answers
20
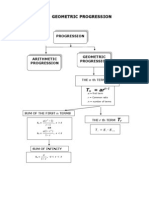
CHAPTER 2 : GEOMETRIC PROGRESSION

2.1 CONCEPT MAP
PROGRESSION
ARITHMETIC
PROGRESSION
GEOMETRIC
PROGRESSION
THE n th TERM
Tn
Tn = arn-1
.a = first term
.r = Common ratio
.n = number of terms
SUM OF THE FIRST n TERMS
Sn =
a (r n 1)
,
r 1
OR
Sn =
THE r th TERM
r >1
16
a (1 r n )
,
1 r
r <1
Tr
T r = S r - S r 1
SUM OF INFINITY
Sn =
a
,
1 r
-1 < r < 1
PROGRESSIONS
( Geometric Progression)
GEOMETRIC PROGRESSION
The sum of the first n term:
The nth term :

Tn = ___________
Sn = ______________
or
Tn = ___________
Sn = ______________
or
a = _______________
r = _______________
l = _______________
n = _______________
2.2
Fill in the blank
Identify characteristics of geometric progression:
EXERCISE 1:
Complete each of the sequence below when give a (fist term ) and r (common ratio) .
17
.r
Example:
a) -3
the first four terms of geometric progression,

-3, (-3)(2)1 = - 6, (-3)(2)2 = -12, (-3)(2)3 = -24
.b)
-2
.c)
.d) -6
-2
.e)
1
2
1
3
.f)
1
y
3
4
y
3
2.3
Determine whether a given sequence is an geometric progression
EXERCISE 2 :
2.3.1
Determine whether a given sequence below is an geometric progression.

.r = common ratio
Example :
a) -8, 4, -2,
.r =
4
1
2
1
=
,
=
8 2
4
2
b) 5, 11, 17, 23,
c) 16, -8, 4,..
d) -20, -50, -30, -35,..
18
(true)
e)
1
2
4
x, x,
x
3
9
27
f) a5, a4 b, a3 b2
g)
h)
1 1
1
,
,
,.
4 12 36
1 1 1
, , ,
27 9 3
EXERCISE 3 :
2.3.2 Given that the first three terms of a geometric progression are below.
Find the value of x
Geometric progression
Example :
a) .x, x + 4, 2x + 2,
Value x
x 4 2x 2
=
x
x4
2
(x + 4) = x(2x + 2)
.x2 + 8x + 16 = 2x2 + 2x
0 = x2 6x 19
0 = (x 8)(x + 2)
.x 8 = 0 @ x + 2 = 0
Hence x = 8 @ x = -2
b) x, x + 2 , x + 3
19
c) x + 3, 5x - 3, 7x + 3
e) x 6, x, 2x + 16
2.4
Determine by using formula:
Tn = arn-1
EXERCISE 4:
20
2.4.1
specific terms in arithmetic progressions
Example :
1. Find the 7 th term of the geometric
progression.
- 8, 4 , -2 , ..
Solution:
4
1
a=-8
r=
=
8 2
1 7-1
T7 = (-8)(
)
2
1
=
8

progression.
16, -8, 4,
3. For the geometric progression

4 2
, , 1 , .. ,find the 9 th term .
9 3

progression
50, 40, 32.
5. Find the 10 th term of geometric

progression a5, a4 b, a3 b2
6. Given that geometric progression

5.6, 1.4, 0.35,
Find the 10th term.
21
2.4.2
Find the number of terms of the arithmetic progression
EXERCISE 5:
Example :
a) 64, - 32, 16,.-
b) 2, -4, 8, 512
1
8
1
1
a = 64, r = 8
2
1
1
64 n1 = 8
2
1 n1 1 1
=

2
64 8
1 n1 1 6 1 3
=

2
2 2
1 n1 1 9
=

2
2
.n - 1 = 9
.n = 10
Tn = -
. c) 405, - 135, 45, -
5
27
.d)
4 2
81
,
, 1.. ,
9 3
16
22
2.5
Find
d) The sum of the first n terms of geometric progressions
e) The sum of a specific number of consecutive terms of geometric progressions
f) The value of n , given the sum of the first n terms of geometric progressions.
Sn =
a (r n 1)
, r >1
r 1
OR
a (1 r n )
Sn =
, r <1
1 r
2.5.1
Find the sum of the first n terms of geometric progressions
EXERCISE 6:
geometric progressions
Find the sum of the first n term
Example :
.a) 2, - 4, 8,
4
.a = 2
r=
= -2
2
b) 5, 10, 20..
c) 12, -6, 3
d)
1
2
4
x, x,
x,.
3
9
27
S7
2(1 (2) 7 )
= 86
1 (2)
S8
S9
S6
23
2.5.2
The sum of a specific number of consecutive terms of geometric progressions
EXERCISE 7:
geometric progressions
Find the sum of the first n term
Example 1
1
.a) 4, 2, 1,
64
.a = 4
r=
1
2
=
4
2
1
64
1
1
4 n1 =
64
2
1 n1 1 1
=

2
4 64
1 n1 1 2 1
=

2
2 2
n1=8
n=9
Tn
4 1 1 / 2
S9 =
1 1 / 2
= 7 63
1, 3, 9,. 2187.
24
64
c) 24, 12, 6, .
2.5.3
3
4
The value of n , given the sum of the first n terms of geometric

progressions.
EXERCISE 8 :
25
2.4
Find :
a) the sum to infinity of geometric progressions
b) the first term or common ratio, given the sum to infinity of geometric
Example :
.a) The first and 4th tems of a geometric progression are
1
27
and
.
2
128
Find the value of r

Solution :
T4 =
27
128
1 3
27
(r ) =
2
128
2

1
(r 3 ) =
27
128
(r 3 ) =
27
3
, Hence r =
64
4
b) The first and 6th tems of a geometric progression are 2
1
1
and 607 .
2
2
Find the value of r
c) The common ratio and 5th tems of a geometric progression are

Find the value of a
26
2
22
and 7
.
3
27
progressions.
S sum to infinity
a
S
1 r
a = first term
r = common ratio
EXERCISE 9:
1.
24, 3.6, 0.54, .
2.
81, -27,9, ..
Find the sum to infinity of a given

geomertric progression below:
Example:
2 2
6, 2, , ,.......
3 9
a=6
2
1
r
6
3
a
S
1 r
6
=
1
1- -
3
9
=
2
3.
1 1 1
, , ,....... ..
2 4 8
27
EXERCISE 10:
1. The sum to infinity of a geometric
progression is 200. Given that the
first
term is 52. Find the common ratio.
2. Given that the common ratio of

1
geometric progression is
. The sum
25
of the first n terms,where n is large
enough such that r n 0 is 75. Find
the first term.
Example:
The sum to infinity of a geometric
progression is 8. Given that the first
term is 2. Find
a) the common ratio
b) the third term
3. The sum to infinity of a geometric

progression is 600 and the common
ratio is 0.4 . Find
a) the first term
b) the minimum number of
terms such that the sum of
terms to be more then 599.
Solution:
a)
S 8
a
8
1 r
2
8
1 r
3
r=
4
b)
28
Tn ar n 1
3
=2
4
9
=
8
31
4. Express each of the recurring decimal below as a fraction in its simplest form.
Example:
Example:
0.3
4.020202
0.3= 0.3 + 0.03 + 0.003 + ..

0.3
1 0.1
0.3
0.9
1
a) 0.444.
4.020202... 4 0.02 0.0002 0.000002 ...

0.02
1-0.01
0.02
=4+
0.99
2
=4
99
=4+
c) 1.121212..
29
b) 0.232323
2.5
d) 5.070707...
Solve problems involving geometric progressions:
EXERCISE 11:
Example:
A garderner has a task of cutting the
grass of a lawn with an area of 1000 m 2 .
On the first day, he cut an area of 16m 2 .
On each successive day, he cuts an area
1.1 times the area that he cut the previous
day the task is completed. Find
a) the area that is cut on the 10th day.
b) The number of the days needed to
complete the task.
Osman is allowed to spend an

allocation of RM1 million where
the maximum withdrawal each day
must not exceed twice the amount
withdrawn the day before. If
Osman withdraws RM200 on the
first day, determine after how
many days the amount of money
allocated will all be used up.
Solution:
a) a=16 , r=1.1
30
Tn ar n 1
T10 16(1.1)9
= 37.73 m 2
b) Sn 1000
1000
16 1.1n -1
1.1-1
160(1.1n 1) 1000
1.1n 1 6.25
1.1n > 7.25
log 1.1n log 7.25

n log1.1 log 7.25
log7.25
n >
log1.1
n >20.79
The smallest integer value of n is 21
hence,the number of the days needed to complete
the task is 21 days.
SPM QUESTIONS:
1. 2003 (Paper 1: No.8)
In a geometric progression, the first term is 64 and the fourth term is 27. Caculate
(a) the common ratio
(b) the sum to infinity of the geometric progression.
[4 marks]
31
2. 2004(Paper 1: No.9)
4
Given a geometric progression y, 2, , p,..... ,express p in terms of y.
y
3. 2004(Paper 1: No.12 )
Express the recurring decimal 0.969696as a fraction in its simplest form.
[4 marks]
4. 2004(Paper2: Section A: No.6)

Diagram 2 shows the arrangement of the first three of an infinite series of similar
triangles. The first triangle has a base of x cm and a height of y cm. The
measurements of the base and height of each subsequent triangle are half of
the measurements of its previous one.
y cm
xcm
Diagram 2
32
(a) Show that the areas of the triangles form a geometric progression and state
the common ratio.
[3 marks]
(b) Given that x= 80 cm and y= 40 cm,
1
(i) determine which triangle has an area of 6 cm 2 ,
4
2
(ii) find the sum to infinity of the areas, in cm , of the triangles. [5 marks]
5. 2005 (Paper 1 : No.10)

The first three terms of a sequence are 2 , x , 8
Find the positive value of x so that the sequence is
(a) an arithmetic progression
(b) a geometric progression
33
[4 marks]
6. 2005 (Paper 1: No. 12)

The sum of the first n terms of the geometric progression 8,24,72,.is 8744.
Find
(a) the common ratio of the progression
(b) the value of n
[4 marks]
ASSESSMENT:
1.
The first three terms of a geometric progression are 2x + 3, x and x 2

with a common ratio r , where -1 < r < 1. Find
(a) the value of x
(b) the sum of the first n terms ,where n is large enough such
that r n 0
34
2.
In the progression 5 , 10 , 20 , 40 , . Find the least number of

terms required such that their sum exceeds 1000.
3.
The third term and the sixth term of a geometric progression are
27 and 8 respectively. Find the second term.
4.
In a geometric progression, the sum of the first five terms is

Given that the common ratio is
31
.
8
1
. Find
2
(a) the first term

(b) the sum of all the terms from the fourth to the sixth term.
35
5.
The third term of a geometric progression exceeds the second term

by 6 while the fourth term exceeds the third term by 2. Find the
sum of the first 5 terms.
ANSWERS:
EXERCISE 1:
b) 3, 6, -12, 24
c) 4, 12, 36, 108
d) -6, 12, 124, 48
1 1 1 1
e)
, , ,
2 6 18 54
y 4 y 2 16 y 3 64 y 4
f)
,
,
,
3
9
27
81
EXERCISE 3:
b) x = -4
c) x = 3
d) x = -12 @ x = 8
EXERCISE 5:
b) n = 9
c) n = 8
d) n = 7
EXERCISE 7:
c) n = 8, S 8 = 3280
d) n = 9, S 9 = -1022
1
e) n = 6, S 6 = 47
4
EXERCISE 2:
a) true
b) false
c) true
d) false
e) true
f) true
g) false
h) true
EXERCISE 4:
1
1. T 7 = 8
1
2. T 8 = 2
26344
3. T 9 =
2304
4. T 3 = 32
b9
5. T 10 = 4
a
6. T 10 = 0.000021
EXERCISE 6:
b) 275
1
c) 8
64
665
d)
729
EXERCISE 8:
b) r = 3
c) a = 3
36
EXERCISE 9:
1. 28.24
3
2. 60
4
3. 1
EXERCISE 10:
2. r=0.74
3. a=72
4. a) 360 b) 7
4
a)
9
23
b)
99
5.
4
c) 1
33
7
d) 5
99
EXERCISE 11:
13 days
SPM QUESTION:
3
1. a) r
b) S 256
4
8
2. p 2
y
32
3.
33
1
4. a) r
4
1
b)i. n=5 ii. 2133
3
5. a) x=5 b) x=4
6. a) r=3 b) n=7
ASSESSMENT:
1. a) x=3 b)
27
2
2. 8
3. 40
1
2
4. a) -2 b)
5. 40
7
16
1
3
37

Progression PDF

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Progression PDF

Uploaded by

Copyright:

Available Formats

http://sahatmozac.blogspot.

CHAPTER 1: ARITHMETIC PROGRESSION

1.1 Identify characteristics of arithmetic progression

Determine whether a given sequence is an

1.3 Determine by using formula:

Solve problems involving arithmetic progressions

The sum of the first n term:

The nth term :

Fill in the blank

1.1 Identify characteristics of arithmetic progression:

1.2 Determine whether a given sequence is an arithmetic progression

b) -20 , -50 , -30 , -35 , . ( ____________________ )

k +3 , 2k + 6 ,8 are the first three terms of an arithmetic progression,find the

Given that x 2 ,5 x, 7 x 4 are three consecutive terms of an arithmetic progression

here x has a positive value. Find the value of x.

1.3 Determine by using formula:

2. Find the 11th term of the arithmetic

4. Find the nth term of the arithmetic

5. Find the 7th term of arithmetic

6. Given that arithmetic progression

2. For the arithmetic progression

3. The sequence 121 , 116 , 111 , . is

4. Find the number of terms of the

3. For the arithmetic progression

2. Find the sum of all the terms of the

How many terms of the arithmetic

1.5 Solve problems involving arithmetic progressions.

The 2nd and 8th terms of an arithmetic

The sum of the first 6 terms of an

4. The sum of the first n terms is given

3. Paper 1: ( no. 11)

5. Paper 2 : ( Section A no.3)

CHAPTER 2 : GEOMETRIC PROGRESSIONS

CONCEPT MAP (GEOMETRIC PROGRESSIONS)

IDENTIFY CHARACTERISTICS OF GEOMETRIC

DETERMINE WHETHER A GIVEN SEQUENCE IS A

DETERMINE BY USING FORMULA

a) specific terms in geometric progressions

2.7 SOLVE PROBLEMS INVOLING GEOMETRIC

CHAPTER 2 : GEOMETRIC PROGRESSION

SUM OF THE FIRST n TERMS

The sum of the first n term:

The nth term :

Fill in the blank

Identify characteristics of geometric progression:

the first four terms of geometric progression,

Determine whether a given sequence is an geometric progression

Determine whether a given sequence below is an geometric progression.

b) 5, 11, 17, 23,

c) 16, -8, 4,..

d) -20, -50, -30, -35,..

Determine by using formula:

specific terms in arithmetic progressions

2. Find the 8 th term of the geometric

3. For the geometric progression

4. Find the 3 th term of the geometric

5. Find the 10 th term of geometric

6. Given that geometric progression

Find the number of terms of the arithmetic progression

. c) 405, - 135, 45, -

Find the sum of the first n terms of geometric progressions

Find the sum of the first n term

The sum of a specific number of consecutive terms of geometric progressions