Professional Documents
Culture Documents
Phase Margin & Gain Margin
Phase Margin & Gain Margin
Uploaded by
Ali Ali Aliali0 ratings0% found this document useful (0 votes)
4 views5 pagesaa
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Documentaa
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
4 views5 pagesPhase Margin & Gain Margin
Phase Margin & Gain Margin
Uploaded by
Ali Ali Alialiaa
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 5
Stability Margins
What is the worst perturbation of the
transfer function that will make the system
marginally stable?
Marginal stability for open loop stable
systems is when the contour goes through
the point (1,0).
Phase Margin & Gain Margin
M. Sami Fadali
Professor of Electrical Engineering
University of Nevada
1
Gain and Phase Margins
Model Perturbation
Gain Margin: gain perturbation that makes
the system marginally stable.
Phase Margin: negative phase perturbation
that makes the system marginally stable.
R(s) +
G(s)
C(s)
G(s)
G(s) = model perturbation
Gain Margin: G(s) = K (gain perturbation)
Phase Margin: G(s) = ej (phase lag
perturbation)
3
Margins on Polar Plot
Definitions of Margins
=gain crossover
/phase crossover
Gain Margin: additional gain that makes the
system on the verge of instability.
Phase Margin: additional phase lag that
makes the system on the verge of
instability.
Polar plot of Unstable System
Point on Bode Plot
Negative real axis for Nyquist plot
.
corresponds to an angle of
Magnitude of unity corresponds to zero dB.
For PM we need to find the phase angle at
magnitude unity (0dB).
For GM we need to find the magnitude at an
angle of
.
Negative GM (dBs) and PM.
7
Bode Plot of Stable System
MATLAB Margin
>> [Gm,Pm,Wcg,Wcp] = margin(g)
Gm =
2.5000
Pm =
22.5359
Wcg =
10.0000 (phase crossover freq.)
Wcp =
6.0783 (gain crossover freq.)
>> margin(g)
9
Gain Margin Calculation
Example: Gain Margin
Multiply numerator and denominator by the
complex conjugate of the denominator.
10
Solve for phase crossover (imaginary part zero)
Equate the imaginary part of the numerator to
zero and solve for the phase crossover
frequency:
Calculate the gain margin
11
12
Phase Margin Calculation
Calculate Gain Margin
Evaluate the magnitude at the phase crossover
frequency
Solve for gain crossover frequency (unity
magnitude)
Calculate the phase margin
13
14
Phase Margin
Phase Margin Calculation
Solve for gain crossover (unity magnitude)
15
16
Delay Margin
Stability Margins
>> g=zpk([],[-1,-5],10)
Nyquist Diagram
1.5
Imaginary Axis
1
0.5
0
System: g
Phase Margin (deg): 104
Delay Margin (sec): 1.12
At frequency (rad/s): 1.62
Closed Loop Stable? Yes
-0.5
= delay margin = time delay for the
system to be on the verge of instability.
Zero/pole/gain:
10
----------(s+1) (s+5)
Transfer function with time delay
>> nyquist(g)
System on verge of instability
-1
-1.5
-1
-0.5
0.5
Real Axis
1.5
17
Delay Margin Calculation
18
Example
Equate angles:
Solve for the delay margin
Same as MATLAB answer.
19
20
You might also like
- Design Via Root Locus and Frequency ResponseDocument15 pagesDesign Via Root Locus and Frequency ResponseBran WzNo ratings yet
- Antenna Azimuth Position Control System Modelling, AnalysisDocument30 pagesAntenna Azimuth Position Control System Modelling, AnalysisMbongeni Maxwell100% (3)
- Lecture 9-10 - Frequency Response MethodsDocument68 pagesLecture 9-10 - Frequency Response MethodsDerrick Maatla Moadi100% (1)
- Frequency ResponseDocument30 pagesFrequency ResponseGovind KumarNo ratings yet
- Design ControllerDocument34 pagesDesign ControllerMaezinha_MarinelaNo ratings yet
- Introduction To Equalization: Guy Wolf Roy Ron Guy ShwartzDocument50 pagesIntroduction To Equalization: Guy Wolf Roy Ron Guy ShwartzShilpi RaiNo ratings yet
- CH5-Frequency Response PDFDocument27 pagesCH5-Frequency Response PDFRidir ZolkefleNo ratings yet
- CS-Lab Assignment-6 1913123Document35 pagesCS-Lab Assignment-6 1913123karthik rajuNo ratings yet
- Frequency Response AnalysisDocument33 pagesFrequency Response AnalysisShiraz HusainNo ratings yet
- ConSys Compre (2017-18)Document2 pagesConSys Compre (2017-18)Dev ShahNo ratings yet
- Aee RCRD FinalDocument16 pagesAee RCRD FinalOCCULTEDNo ratings yet
- Unit III Two MarksDocument6 pagesUnit III Two Marksniya enzieNo ratings yet
- 1 - Compensator Design Procedure - Lead - Lag - With ExamplesDocument12 pages1 - Compensator Design Procedure - Lead - Lag - With ExamplesMadhav SNo ratings yet
- MIT16 30F10 Lec04Document16 pagesMIT16 30F10 Lec04Cristian NapoleNo ratings yet
- Phase Lead Compensator Design Using Bode Plots: ObjectivesDocument7 pagesPhase Lead Compensator Design Using Bode Plots: ObjectivesMuhammad AdeelNo ratings yet
- Control Lab NoteDocument19 pagesControl Lab NoteSK-062; 470; Afsana Anjum AkhiNo ratings yet
- Introduction To Switched-Mode Converter Modeling Using MATLAB/SimulinkDocument37 pagesIntroduction To Switched-Mode Converter Modeling Using MATLAB/SimulinkAhana MalhotraNo ratings yet
- The Frecuency-Response Design Method: Universidad Politecnica SalesianaDocument28 pagesThe Frecuency-Response Design Method: Universidad Politecnica SalesianaFabiola ChachaNo ratings yet
- Tutorial II DesignDocument4 pagesTutorial II Designgeofrey fungoNo ratings yet
- Stability, Gain Margins, Phase MarginsDocument10 pagesStability, Gain Margins, Phase MarginsRavinder KumarNo ratings yet
- Analog Integrated Circuit Design: Nagendra KrishnapuraDocument26 pagesAnalog Integrated Circuit Design: Nagendra KrishnapuraAnkit Bhoomia0% (1)
- CS Exp 8Document7 pagesCS Exp 8Anirudh MittalNo ratings yet
- Notes Tee602 Bode Plot PDFDocument23 pagesNotes Tee602 Bode Plot PDFtansnvarmaNo ratings yet
- Solutions To Homework 4: Problem 1 (15 Points)Document15 pagesSolutions To Homework 4: Problem 1 (15 Points)joa91189100% (1)
- EN5001 - Electronic Control Systems: Department of Electronic and Telecommunication EngineeringDocument11 pagesEN5001 - Electronic Control Systems: Department of Electronic and Telecommunication EngineeringSurangaGNo ratings yet
- CASERES - CoNTROL LABDocument6 pagesCASERES - CoNTROL LABVan Eldridge Kyle CaseresNo ratings yet
- Geng4402 - Assignment 2: Question 1 - Nyquist Plot/Frequency Response PerformanceDocument9 pagesGeng4402 - Assignment 2: Question 1 - Nyquist Plot/Frequency Response PerformanceangelosoutiNo ratings yet
- Notes Tee602 Bode PlotDocument23 pagesNotes Tee602 Bode PlottansnvarmaNo ratings yet
- Bode Plot Design PDFDocument15 pagesBode Plot Design PDFsmileuplease8498No ratings yet
- Prof Chiu Lu EisenhowerDocument1 pageProf Chiu Lu Eisenhowersanjujoshhi7550No ratings yet
- Time & Frequency Response of The System Using MATLAB: SoftwareDocument9 pagesTime & Frequency Response of The System Using MATLAB: SoftwareVenkatesh KumarNo ratings yet
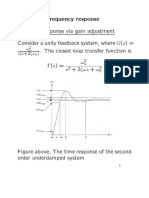
- Design via frequency response Transient response via gain adjustment Consider a unity feedback system, where G(s) = - The closed loop transfer function is T (s) = ω s + 2ζωs + ωDocument12 pagesDesign via frequency response Transient response via gain adjustment Consider a unity feedback system, where G(s) = - The closed loop transfer function is T (s) = ω s + 2ζωs + ωmdthNo ratings yet
- (VTC2006) (Synchronization and Channel Estimation in Cyclic Postfix Based OFDM System)Document18 pages(VTC2006) (Synchronization and Channel Estimation in Cyclic Postfix Based OFDM System)jkkim13No ratings yet
- Lecture 8 - Specification and Limitations: K. J. ÅströmDocument12 pagesLecture 8 - Specification and Limitations: K. J. ÅströmEdutamNo ratings yet
- U2 Bode PlotDocument41 pagesU2 Bode PlotThalía LuceroNo ratings yet
- Phase Lead and Lag CompensatorDocument8 pagesPhase Lead and Lag CompensatorNuradeen MagajiNo ratings yet
- Clase 17 Diseño Por Medio Del LGR PIDDocument46 pagesClase 17 Diseño Por Medio Del LGR PIDCristhian RamosNo ratings yet
- EC602 Control Q Bank 2023Document9 pagesEC602 Control Q Bank 2023ROHAN CHOWDHURYNo ratings yet
- Frequency Response Analysis: Section 6Document45 pagesFrequency Response Analysis: Section 6Ahmed HassanNo ratings yet
- PD, PI, PID Compensation: M. Sami Fadali Professor of Electrical Engineering University of NevadaDocument42 pagesPD, PI, PID Compensation: M. Sami Fadali Professor of Electrical Engineering University of NevadaAsghar AliNo ratings yet
- 6 Signal Flowgraphs: 6.1 DescriptionDocument14 pages6 Signal Flowgraphs: 6.1 DescriptionYuqi ZhaoNo ratings yet
- Frequency Response DesignDocument22 pagesFrequency Response Designمعروف المحجريNo ratings yet
- Ee481 p11 Root Locus DesignDocument77 pagesEe481 p11 Root Locus DesignDwi Ika BasithaNo ratings yet
- Compensator Design II PDFDocument37 pagesCompensator Design II PDFMani Vannan SoundarapandiyanNo ratings yet
- Non-Idealities of Switched Capacitor Filter DesignDocument19 pagesNon-Idealities of Switched Capacitor Filter Designhariprasath_vNo ratings yet
- Module 2 - 2Document68 pagesModule 2 - 2abcdNo ratings yet
- Bode Plot2019Document77 pagesBode Plot2019Krushnasamy SuramaniyanNo ratings yet
- Control de ProcesosDocument12 pagesControl de ProcesosLuis Fernando Pucuhuanca PachecoNo ratings yet
- Unit Iii Frequency ResponseDocument28 pagesUnit Iii Frequency ResponseRaghu RamNo ratings yet
- Lecture 380-21-202 GM and PM NyquistDocument17 pagesLecture 380-21-202 GM and PM Nyquistyfm9bnzb2gNo ratings yet
- Chapter 4 Characteristics of Closed-Loop SystemsDocument25 pagesChapter 4 Characteristics of Closed-Loop SystemsDio ChanNo ratings yet
- Design Problem Matlab Project TFDocument19 pagesDesign Problem Matlab Project TFhumayun azizNo ratings yet
- Matlab Tutorial Part 4: Frequency Domain Analysis and DesignDocument10 pagesMatlab Tutorial Part 4: Frequency Domain Analysis and DesignRobert RoigNo ratings yet
- Control Systems Systems and Their Representations Unit-1: Ms. P. Geethanjali Asst. Professor (SR) SelectDocument72 pagesControl Systems Systems and Their Representations Unit-1: Ms. P. Geethanjali Asst. Professor (SR) SelectVijay IndukuriNo ratings yet
- Repetitive ControlDocument22 pagesRepetitive ControlShri KulkarniNo ratings yet
- BodeDocument8 pagesBodeeeetistNo ratings yet
- Design of Lead and Lag CompensatorDocument3 pagesDesign of Lead and Lag CompensatorShiva Bhasker ReddyNo ratings yet
- علي احمد جباره تقرير تقرير مختبر الكونترولDocument6 pagesعلي احمد جباره تقرير تقرير مختبر الكونترولسيد نعيمNo ratings yet
- Experiment No. 5 Study of The Effect of A Forward-Path Lead Compensator On The Performance of A Linear Feedback Control SystemDocument3 pagesExperiment No. 5 Study of The Effect of A Forward-Path Lead Compensator On The Performance of A Linear Feedback Control SystemSubhaNo ratings yet
- Near-Death-Experiences: Between Spiritual Transmigration and Psychopathological HallucinationsDocument50 pagesNear-Death-Experiences: Between Spiritual Transmigration and Psychopathological HallucinationsTejaswi J DamerlaNo ratings yet
- Program Schedule IshaDocument3 pagesProgram Schedule IshaTejaswi J DamerlaNo ratings yet
- The Inner Engineering Retreat Is A Unique Opportunity To Imbibe The Timeless Science of YogaDocument3 pagesThe Inner Engineering Retreat Is A Unique Opportunity To Imbibe The Timeless Science of YogaTejaswi J DamerlaNo ratings yet
- Health: Green Coffee Extract CapsulesDocument2 pagesHealth: Green Coffee Extract CapsulesTejaswi J DamerlaNo ratings yet
- StepsDocument1 pageStepsTejaswi J DamerlaNo ratings yet
- State Bank of India Clerks PDFDocument2 pagesState Bank of India Clerks PDFTejaswi J DamerlaNo ratings yet