Understanding the Kellogg Equivalent Pressure Method for piping flanges

Remarks
1. This method is a gasket load calculation.
2. This paper counts the gasket load in terms of force per unit
length of circumference, as this approach is usual in the circular plate
theory.
3. For calculation of the reaction on free-to-rotate edge, the
circular plate theory gives results that are quite insensitive vs. variations
of plate rigidity.

a
G

The theory assumes that the flange is a circular plate.

bolts

H G0 =

HG0

HG0

Fbolts

2 a
external loads.

is the gasket load for the case no pressure, no

G
No pressure, no external loads

HG (p)

H G ( p) = H G0

bolts

Fpressure

HG (p)

Fpressure

2 a
is the gasket load for the case internal pressure, no external loads.
Fpressure = a 2 p
and

Internal pressure, no external loads

F
F

ap
2
Remark: A pressure load is decreasing the gasket reaction.
H G ( p) = H G 0

G=2a

bolts

H G ( F) = H G0

HG (F)

HG(F)

G=2a

2 a
is the gasket load for the case no pressure, external tensile force.
Remarks: - A tensile force F > 0 is decreasing the gasket load.
- A compressive force F < 0 is increasing the gasket load.

No pressure, external tensile force

-1-

Understanding the Kellogg Equivalent Pressure Method for piping flanges

M
F

maxHG (M)

A bending moment is changing the gasket load, but H G ( M ) is variable

along the gasket circumference.
The gasket load can be described by the following model, based on the
theory of circular plates.

bolts

minH G(M)

G=2a
M

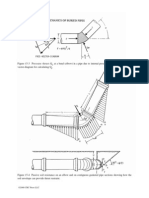
No pressure, external bending moment

-p

a
G

-V

(Vmax)

(Vmin)

ds=ad

a cos

G=2a

pa
cos is the evaluation of the edge reaction
4
following the circular plate theory
(see Theory of Plates and Shells by S. Timoshenko and S.
V=

Woinowsky-Krieger, Second edition, 1959, paragraph 63

Circular Plates under Linearly Varying Loads)

and

a 3 p
pa

M=4
cos (a cos ) ad =
4
4

is the moment equation.

It results:
4M
p= 3
a
pa 4 M a M
Vmax =
=
=
4 a 3 4 a 2
H G ( M ) = H G0 + Vmax cos = H G 0 +

M
cos
a 2

a 2
is the minimum gasket load for the case no pressure,
external bending moment.
min H G ( M ) = H G0

-2-

Understanding the Kellogg Equivalent Pressure Method for piping flanges

THE FOLLOWING EQUIVALENCES CAN BE WRITTEN:

F

The minimum gasket load is

M
F
min H G (M , F ) = H G 0 2
2a
a

M
F

bolts

max HG(M,F)

min H G(M,F)

The maximum gasket load is

M
F
max H G (M , F ) = H G 0 + 2
2a
a

G=2a
No pressure, external bending moment
and external tensile force

IS EQUIVALENT WITH
Feq
F

The equivalence is considered in terms

of tensile force that gives the reaction on
gasket equal to the minimum gasket load given
by the external loads:

bolts

HG (Feq )

min H G ( M , F ) = H G ( Feq ) or

HG (Feq )

G=2a
No pressure, equivalent tensile force

IS EQUIVALENT WITH

Feq
F
M
H G0 2 +
= H G0
2a
2a
a
That means:
Feq
M
F
= 2+
, i.e.
2 a a
2 a
2M
4M
Feq = F +
=F+
a
G
Remark: This equivalence is conservative made
and is really true just for a point, not for the entire gasket
circumference.

Feq pressure
F

HG (peq )

The equivalence is considered in terms of pressure that

gives the same effect as Feq , i.e.

bolts

HG (peq )

p eq a 2 = Feq

or p eq =
G=2a
Equivalent pressure, no external loads

-3-

1
2M
F
2M
F+
= 2 + 3
2
a a
a
a

=
G
a=
2

4 F 16M
+
G 2 G 3

Understanding the Kellogg Equivalent Pressure Method for piping flanges

GASKET LOAD LIMITS

Fpressure

For the tensile loaded part of the flange, the minimum

gasket load is:
Fpressure + Feq pressure
a 2 (p + peq )
H G (peq ,p) = H G 0
= HG0
2 a
2 a

Feq pressure
F

bolts

HG (peq ,p)

HG (peq ,p)

This load must be limited to the value corresponding to

the rating pressure.

G=2a
Internal pressure, equivalent pressure

versus the limit given by the rating pressure

FRATING pressure
F

bolts

H G ( p RATING ) = H G0
HG (pRATING )

a 2 p RATING
2 a

HG (pRATING )

G=2a

The gasket tightness condition means to accept for the gasket load only values that are greater than the
value corresponding to the rating pressure.
The condition H G ( p eq , p) H G ( p RATING ) means p + p eq p RATING .

For the compressed loaded part of the flange, the maximum gasket load is:
M
F
max H G ( M , F ) = H G0 + 2
, where F > 0 is a tensile force, F < 0 is a compressive force.
2 a
a
1
M
F
This load gives a compressive stress for the gasket: H G0 + 2
that may be limited to a
b
2 a
a
maximum stress on the gasket. This condition is not covered by limiting p + p eq p RATING .

-4-