CONFIDENTIAL* 2

1
1. (i) Find ∫x 2
dx [2 marks]
dy 1
(ii) The gradient of a curve is given by = 2 . Find the equation of the curve, given that it
dx x
passes through the point (1, 3). [2 marks]

2. If A, B and C are arbitrary sets, show that

[( A − B ) ∩ ( A − C )] ∪ B ∪ C = A ∪ B ∪ C [4 marks]

1
3. Using the trapezium rule, with 5 ordinates, evaluate ∫ −1
1 + e x dx, giving your answer correct to
three decimal places. [4 marks]

4. Find the square root of − 5 + 12i. [5 marks]

1 1
5. Expand (1 + 2 x ) 3 up to and including the term in x 3 . Use your series to obtain a value for (1.04 ) 3
giving five decimal places in your answer. [6 marks]

2 1 1
6. Show that can be expressed as − . [2 marks]
x(x + 2) x x+2
n
3 9 3(2n + 3)
By using the method of differences, show that ∑ x(x + 2) = 4 − 2(n + 1)(n + 2) .
x =1
[4 marks]

3 3 3 3
Hence, find the sum of the series + + + ... + . [2 marks]
1× 3 2 × 4 3 × 5 10 × 12

 0 2 − 1  2 − 8 6
   
7. The adjoint of matrix A =  0 8 − 1 is  − 4 4 0 .
 4 10 − 1  − 32 k 0 
   
(a) Show that matrix A is non-singular. [3 marks]
(b) Find
(i) the value of k, [2 marks]
(ii) the inverse of matrix A. [2 marks]
 3 1 4a + 10b 
 
The matrix  2b − c 0 8b − c  where a, b and c are constants, is a symmetric matrix.
 29 + c 16 1 
 
(c) Write a system of equations in terms of a, b and c. [2 marks]
(d) Hence, find the values of a , b and c using matrix. [4 marks]

d2y dy
8. Given y = e −2 x cos 3 x, prove that 2
+ 4 + 13 y = 0. [5 marks]
dx dx

954/1 [Turn over

*This question paper is CONFIDENTIAL until the examination is over. CONFIDENTIAL*
CONFIDENTIAL* 3
9. (a) The continuous function f ( x ) is defined by:
 2( x − 1)
 , x <1
f (x ) =  x − 1
 4 x − k , x ≥ 1 and k is a constant
Find
(i) the value of lim− f ( x ), [2 marks]
x →1
(ii) the value of k. [2 marks]
(b) The functions f and g are defined by:
1
f :x→ ,x<0
1+ x2
g : x → − 1− x2 , −1 ≤ x ≤ 1
(i) By using sketch graphs of the functions f and g on the same axes, determine the
range of function f and function g. [5 marks]
(ii) Determine whether the function f o g exists. [2 marks]
(iii) Explain why the function f has an inverse function, f −1 . Find the inverse function
−1
f in the same form as given for f. [3 marks]

5
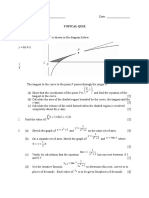
10. Show that the equation 2 ln x = has only one real root that lies between x = 2 and x = 3.
x
[3 marks]
5
Use Theorem Newton Raphson to find the root of 2 ln x = correct to 3 decimal places by using
x
2.5 as the first approximation. [5 marks]
y
11. A (2, 9)
•

• B (10, 3)

O x
The diagram shows a circle which passes through the point A (2, 9) and B (10, 3). AB is a diameter
of the circle.
(i) Calculate the radius of the circle and the coordinates of the centre. [4 marks]
(ii) Show that the equation of the circle may be written in the form
x 2 + y 2 − 12 x − 12 y + 47 = 0. [3 marks]
(iii) The tangent to the circle at the point B cuts the x-axis at C. Find the coordinates of C.
[6 marks]

3x − 9
12. Find the coordinates of the stationary point on the curves y = 2
. Determine the nature of
x −x−2
the stationary points.
Sketch the curve and state the equation of asymptotes.
Show that the equation of the curve can be written in the form yx 2 − ( y + 3)x − (2 y − 9 ) = 0 and has
no real root if ( y − 3)(3 y − 1) < 0. [16 marks]

954/1
*This question paper is CONFIDENTIAL until the examination is over. CONFIDENTIAL*