Professional Documents
Culture Documents
ANOVA - ANalysis of VAriance Between Groups
ANOVA - ANalysis of VAriance Between Groups
Uploaded by
Ravi Gowtham0 ratings0% found this document useful (0 votes)
35 views1 pageThe size of maple leaves depends on the location of the trees. Maple leaves under the shade of tall oaks are smaller than the maple leaves from trees in the prairie. If some group's average leaf-size is "unusually" large or small, it is unlikely to be just "chance"
Original Description:
Original Title
ANOVA_ ANalysis of VAriance Between Groups
Copyright
© Attribution Non-Commercial (BY-NC)
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThe size of maple leaves depends on the location of the trees. Maple leaves under the shade of tall oaks are smaller than the maple leaves from trees in the prairie. If some group's average leaf-size is "unusually" large or small, it is unlikely to be just "chance"
Copyright:
Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
35 views1 pageANOVA - ANalysis of VAriance Between Groups
ANOVA - ANalysis of VAriance Between Groups
Uploaded by
Ravi GowthamThe size of maple leaves depends on the location of the trees. Maple leaves under the shade of tall oaks are smaller than the maple leaves from trees in the prairie. If some group's average leaf-size is "unusually" large or small, it is unlikely to be just "chance"
Copyright:
Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 1
ANOVA: ANalysis Of VAriance between groups
Page 1
ANOVA: ANalysis Of VAriance between groups
Click here to start ANOVA data entry Click here for copy & paste data entry You might guess that the size of maple leaves depends on the location of the trees. For example, that maple leaves under the shade of tall oaks are smaller than the maple leaves from trees in the prairie and that maple leaves from trees in median strips of parking lots are smaller still. To test this hypothesis you collect several (say 7) groups of 10 maple leaves from different locations. Group A is from under the shade of tall oaks; group B is from the prairie; group C from median strips of parking lots, etc. Most likely you would find that the groups are broadly similar, for example, the range between the smallest and the largest leaves of group A probably includes a large fraction of the leaves in each group. Of course, in detail, each group is probably different: has slightly different highs, lows, and hence it is likely that each group has a different average (mean) size. Can we take this difference in average size as evidence that the groups in fact are different (and perhaps that location causes that difference)? Note that even if there is not a "real" effect of location on leaf-size (the null hypothesis), the groups are likely to have different average leaf-sizes. The likely range of variation of the averages if our location-effect hypothesis is wrong, and the null hypothesis is correct, is given by the standard deviation of the estimated means: /N where is the standard deviation of the size of all the leaves and N (10 in our example) is the number of leaves in a group. Thus if we treat the collection of the 7 group means as data and find the standard deviation of those means and it is "significantly" larger than the above, we have evidence that the null hypothesis is not correct and instead location has an effect. This is to say that if some (or several) group's average leaf-size is "unusually" large or small, it is unlikely to be just "chance". The comparison between the actual variation of the group averages and that expected from the above formula is is expressed in terms of the F ratio: F=(found variation of the group averages)/(expected variation of the group averages) Thus if the null hypothesis is correct we expect F to be about 1, whereas "large" F indicates a location effect. How big should F be before we reject the null hypothesis? P reports the significance level. In terms of the details of the ANOVA test, note that the number of degrees of freedom ("d.f.") for the numerator (found variation of group averages) is one less than the number of groups (6); the number of degrees of freedom for the denominator (so called "error" or variation within groups or expected variation) is the total number of leaves minus the total number of groups (63). The F ratio can be computed from the ratio of the mean sum of squared deviations of each group's mean from the overall mean [weighted by the size of the group] ("Mean Square" for "between") and the mean sum of the squared deviations of each item from that item's group mean ("Mean Square" for "error"). In the previous sentence mean means dividing the total "Sum of Squares" by the number of degrees of freedom.
Why not just use the t-test?
The t-test tells us if the variation between two groups is "significant". Why not just do t-tests for all the pairs of locations, thus finding, for example, that leaves from median strips are significantly smaller than leaves from the prairie, whereas shade/prairie and shade/median strips are not significantly different. Multiple t-tests are not the answer because as the number of groups grows, the number of needed pair comparisons grows quickly. For 7 groups there are 21 pairs. If we test 21 pairs we should not be surprised to observe things that happen only 5% of the time. Thus in 21 pairings, a P=.05 for one pair cannot be considered significant. ANOVA puts all the data into one number (F) and gives us one P for the null hypothesis.
http://www.physics.csbsju.edu/stats/anova.html
7/10/2012 10:15:11 AM
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5808)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1092)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (843)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (590)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (897)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (540)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (346)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (122)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (401)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- 1 PRISM Basic Guide v4Document59 pages1 PRISM Basic Guide v4Maria Rolenza PaladoNo ratings yet
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Abs HaldexDocument2 pagesAbs HaldexBom_Jovi_681No ratings yet
- Ejemplos de Ensayos de Discurso PersuasivoDocument6 pagesEjemplos de Ensayos de Discurso Persuasivoz0s1nusef0l3100% (2)
- Pass Microsoft 70-741 Exam With 100% Guarantee: Networking With Windows Server 2016Document34 pagesPass Microsoft 70-741 Exam With 100% Guarantee: Networking With Windows Server 2016lucasNo ratings yet
- HCSCA112 Dual-System Hot StandbyDocument31 pagesHCSCA112 Dual-System Hot Standbymangla\No ratings yet
- 577013-614 Veeder-Root Dispenser Interface Module (DIM) For TLS-350R Systems Installation ManualDocument24 pages577013-614 Veeder-Root Dispenser Interface Module (DIM) For TLS-350R Systems Installation Manualjose moralesNo ratings yet
- Controler Thermoflow TP4Document5 pagesControler Thermoflow TP4Paulo CostaNo ratings yet
- NAV2013 01 Reporting PDFDocument82 pagesNAV2013 01 Reporting PDFMiguel De Dios SinovasNo ratings yet
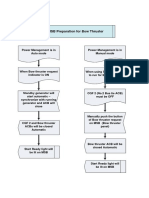
- Bow Thruster Starting ProcedureDocument2 pagesBow Thruster Starting ProcedureThe CapitalNo ratings yet
- Service Notes: Issued by RJADocument15 pagesService Notes: Issued by RJAcarlosNo ratings yet
- STEM in TVET Learning Design FrameworkDocument61 pagesSTEM in TVET Learning Design Frameworkprofjay2023No ratings yet
- Deploying The AlienVault HIDS Agents in AlienVault USM v5Document5 pagesDeploying The AlienVault HIDS Agents in AlienVault USM v5trollcapoeiraNo ratings yet
- App Inventor Cheat SheetDocument9 pagesApp Inventor Cheat SheetNAIR KRISHNA RAVEENDRANNo ratings yet
- Performance Tuning Addedinfo OracleDocument49 pagesPerformance Tuning Addedinfo OraclesridkasNo ratings yet
- FreeBitcoin Script Roll 10000Document4 pagesFreeBitcoin Script Roll 10000shakilanepaliNo ratings yet
- Prog5 ModuleDocument268 pagesProg5 ModuleNica Marie LumbaNo ratings yet
- Temperature Sensor With Buffer-Chain Based Time-To-Digital Converter For Ultralow Voltage OperationDocument14 pagesTemperature Sensor With Buffer-Chain Based Time-To-Digital Converter For Ultralow Voltage OperationJames MorenoNo ratings yet
- Ada4522 1 - 4522 2 - 4522 4Document32 pagesAda4522 1 - 4522 2 - 4522 4Saad AbdullahNo ratings yet
- Proposed Revisions and Addendum On Students' HandbookDocument9 pagesProposed Revisions and Addendum On Students' HandbookHarry Lord M. BolinaNo ratings yet
- Module 3: Hardware-Software Synchronization: Mazen A. R. SaghirDocument50 pagesModule 3: Hardware-Software Synchronization: Mazen A. R. SaghirYehya El hassanNo ratings yet
- TP4000ZC Serial ProtocolDocument2 pagesTP4000ZC Serial ProtocolBluff Flers100% (2)
- TruVista CPNI Cert StatementDocument3 pagesTruVista CPNI Cert StatementFederal Communications Commission (FCC)No ratings yet
- 02 OHC508203 USCDB Principle With Operation and Maintenance (VHSS)Document104 pages02 OHC508203 USCDB Principle With Operation and Maintenance (VHSS)rolandomhNo ratings yet
- Cellular Networks - Positioning Performance Analysis ReliabilityDocument416 pagesCellular Networks - Positioning Performance Analysis Reliabilitystranger_1No ratings yet
- 1982 BMW E528 Electrical Troubleshooting Manual PDFDocument77 pages1982 BMW E528 Electrical Troubleshooting Manual PDFwilderNo ratings yet
- Pumping PDFDocument3 pagesPumping PDFAmit KumarNo ratings yet
- Nokia 9500mpr Mss Indoor PDFDocument2 pagesNokia 9500mpr Mss Indoor PDFMED MOHNo ratings yet
- HDFC Ergo SME HandbookDocument56 pagesHDFC Ergo SME HandbookThe LoanWalaNo ratings yet
- The History of Project ManagementDocument9 pagesThe History of Project ManagementFabio Nelson Rodriguez DiazNo ratings yet
- SYNOPSIS (HOTEL MANAGEMENT SYSTEM Project) 1Document14 pagesSYNOPSIS (HOTEL MANAGEMENT SYSTEM Project) 1Sagar ChakrabartyNo ratings yet