Dynamics of electrons on a lattice - Eective mass

Notes, PHYS208, 1995-2008 - L. Kocbach, Univ. Bergen

Slides version: march 2008
1 0.5 0 0.5 1
0
1
2
3
4
5
6
ka/
(a) Band E
b
= 3 2 cos(ka)
1 0.5 0 0.5 1
3
2
1
0
1
2
3
(b) Velocity v
g
= 2 sin(k)
ka/
1 0.5 0 0.5 1
3
2
1
0
1
2
3
ka/
(c) Inverse eff.m. 1/m* = 2 cos(k)
1 0.5 0 0.5 1
3
2
1
0
1
2
3
ka/
(d) Effective mass m*
Prolog
The concept of Group velocity
We start with a pulse which is a superposition of plane waves. The medium is
such that there is a general relation between wavenumber and frequency
= (k)
i.e. the medium is called dispersive. The time developement of the pulse is
thus
(x, t) =
_
dk

(k)e
i[kx(k)t]
There is also a question about 2 factor. Here it is swallowed by

(k).
(Shapes of pulses: broad frequency spectrum, sharp time; narrow frequency,
long duration, close to monochromatic - or clean tone). Remember by ute
and guitar (which is which?).
The spectrum of the pulse is such that the it is peaked at a certain value k
0
,
such that
max

(k) =

(k
0
)
If the spectral distribution

(k) is suciently narrow in k and limited to narrow
region arround k
0
, we can use a linear approximation for (k)
(k) = (k
0
) +
d
dk
(k k
0
) =
0
+
d
dk
(k k
0
)
By simply setting t=0
(x, 0) =
_
dk

(k)e
i[kx]
This can easily be transformed to
e
i[k
0
x]
_

dk

(k)e
i[(kk
0
)x]
e
i[k
0
x]
_

dk

(k

+ k
0
)e
i[k

x]
We can dene the envelope (or modulation) as
M(x) = e
i[k
0
x]
(x, 0) =
_

dk

(k

+ k
0
)e
i[k

x]
The inverse relation (or denition) for the wavenumber function:

(k) =
1
2
_
dx(x, 0)e
i[kx]
Now we go back to
(x, t) =
_
dk

(k)e
i[kx(k)t]
and transform it like this
_
dk

(k)e
i[k
0
x]
e
i(kk
0
)x
e
i
0
t
e
i[
d
dk
(kk
0
)t]
after rearrangement
e
i[k
0
x]
e
i
0
t
_
dk

(k)e
i(kk
0
)x
e
i[
d
dk
(kk
0
)t]
with anticipated change of variables
(k k
0
) = k

We rewrite this as
e
i[k
0
x
0
t]
_
dk

(k)e
i[(kk
0
)x
d
dk
(kk
0
)t]
and then obtain
e
i[k
0
x
0
t]
_
dk

(k

+ k
0
)e
i[k

xk
d
dk
t]
or rearranged as
(x, t) e
i[k
0
x
0
t]
_
dk

(k

+ k
0
)e
ik

[x
d
dk
t]
With the denition of the envelope above
M(x) =
_

dk

(k

+ k
0
)e
i[k

x]
the (x, t)becomes
(x, t) e
i[k
0
x
0
t]
M
_
x
d
dk
t
_
We thus see that provided that the integral over k

is peaked close enough to

k
0
so that the linear approximation holds, the wave propagates as a plane wave
e
i[k
0
x
0
t]
modulated by the envelope M
_
x
d
dk
t
_
which moves with velocity
v
g
=
d
dk
.
Note that if (k) = ck, then the approximation is in fact an exact expression
and the group velocity is the same as the phase velocity c.
In general, the approximation does not display the fact that the envelope
M (x) is in fact a function of time, M (x, t) . Generally, a pulse broadens in
the dispersive medium.
Quantum - not semiclassical
In most of the textbooks on Solid State Physics this subject is treated in a so
called semiclassical approximation. It is my impression that though the usual
treatment gives a correct result, it is not really understandable, and in some
cases even contains some wrong elements. (Especially in Kittels book)
In this note we propose an alternative form to some steps in Kittels book,
obtain the known result, and we also bring a few further illustrations of the
concept of the eective mass. The present approach seems to be well under-
stood by the students. (Note: not all steps are found in Ashcroft and Mermin!
But some are there.)
1. Overview
Deriving the equation for u
,

k
is more or less straightforward from the
Schr odinger equation for e
i

kx
u
,

k
(We use x for the electron coordi-
nate)
Finding the expectation value of velocity from the expectation value of
momentum
Discussing periodic potential combined with a potential for a constant
force
We establish that the local band energies follow the additional potential
responsible for the (constant) force, i.e. the energies of states in the band
depend on position. Variation from = V , see in the text.
We assume a motion of a wavepacket. Then we can argue that since
the wavepacket is moving, i.e. changing its position, it must change its
(middle) value of

k. From = V then follows

k
dt
=
1
h

F. (derived
in 1 dimension for simplicity)
An expression is derived for acceleration, the concept of (inverse) eective
mass arises
The eective mass is discussed for the simple model band
2. Velocity for Bloch electrons - like group velocity
Now we shall derive the expectation value of momentum in a Bloch state, and
we shall see that it gives the same value as mv
g
,
i.e. mass times group velocity - like expression.
We start from the equation for the periodic function u
,

k
(x)
_

h
2
2m
_
+ i

k
_
2
+ U(r)
_
u
,

k
= (k) u
,

k
take

k
x

k
x
_
+ i

k
_
2
2 i
_
+ i

k
_

h
2
m
i
_
+ i

k
_

h
m
_
i h

x
+ hk
x
_
This was only the part corresponding to the [.....] part. Taking the whole
k
x
-derivative and multiplying by u

k
and integrating, we get
h
m
_
u

k
_
i h

x
+ hk
x
_
u
,

k
+
_
u

k
H
_
u
,

k
k
x
_
=
_
u

k
_
(k)
k
x
_
u
,

k
+
_
(k)u

k
_
u
,

k
k
x
_
We combine the second terms on each side, they give
_
_
u

k
(H (k))
_
_
u
,

k
k
x
_
The term in the {.....} is zero ( Complex Conjugation ) We are then left with
h
m
_
u

k
_
i h

x
+ hk
x
_
u
,

k
=
_
u

k
_
(k)
k
x
_
u
,

k
or simply
h
m
_
u

k
_
i h

x
+ hk
x
_
u
,

k
=
_
(k)
k
x
_
This gives, going back to the whole wavefunctions
,

k
h
m
_

k
_
i h

x
_

k
=
(k)
k
x
i.e. we can write that
1
h
(k)
k
x
=
1
m
p
x
v
x

i.e. meaning the expectation value of momentum divided by mass, which

classicaly is velocity, and this expresion has the same form as the group velocity.
Note that we have derived this by manipulations with symbols, instead of
refering directly to group velocity argument. Remember, (v
g
)
x
= /k
x
etc.
3. Bloch electrons and constant force potential
V (x) =

F x
The picture must be discussed in detail: what do the inclined bands mean.
(x) = V (x)
(f)
+ =
E
E
2
1
(a)
(b)
(c)
(d)
(e)
Figure 1: Potentials: Periodic plus constant eld
(c)
E
E
2
1
(a)
(b)
Figure 2: Bands in inclined potentials
L
(a)
(b)
(c)
(d)
Figure 3: This gure shows a construction of position dependent bands in the
presence of an additional potential. The cut (a) shows a region of length L
which is sucient to establish a quasicontinuous band. Cut (b) shows the
total potential over the region of n L, (n = 3). Cut (c) shows that how
we can chose a sequence of segments of length L, where each of the centers
of the segments we can identify a local band structure. Cut (d) shows the
stepwise approximation to the total potential. The dotted horizontal lines
show a corresponding approximation to the macroscopic potential, i.e. as
piecewise constant over each segment of length L.
E being the energy of a state, or central energy or a wave packet, it will
correspond to dierent at the varying positions. It is easy to see that
= V
Since the relation between and k is identical in each of the segments, we can
e.g. write for each position x

k
(x) = (k(x))
where the function (k) is the relation between energy and wavenumber for
force-free case.
For a given wavepacket, we can write x = v
g
(x)t, where we already indicate
that even the group velocity can - and will - depend on the position.
We can thus write
k
x

k
v
g
(x)t
Once we have established this, we can go to a limiting chain
dk
dt
= v
g
(x)
dk
dx
=
1
h
d
dk
dk
dx
L
x
1
( )
x
1 ( )
x
3
( )
x
2
E
wavepacket
( x ) V
x
1
( ) k
x
2
( ) k ( x ) V
)
3
x ( k
x
2
x
3
Figure 4: This gure also shows a construction of position dependent bands,
but now extended by showing how the other quantities are changing. In par-
ticular, it shows why the wavenumber k is function of position, by showing the
bands displaced according to the changing potential energy.
This can be continued by realizing that = V ,
dk
x
dt
=
1
h

x
=
1
h
V
x
i.e.
dk
x
dt
=
F
x
h
4. Eective mass
We continue by considering the time developement of the group velocity. As
far as the wavepacket is changing the middle energy (x) and wavenumber

k(x), also the group velocity v

g
will be changing along x.
In the following we mean v
g
when using v.
In the same way as befoer, we can talk about a time derivative of a quantity,
in the sense that the time species the position of the wave packet x(t).
We thus write
dv
i
dt
=
d
dt
1
h
d
dk
i
=
1
h
d
dk
i
_
d
dt
_
To evaluate the Time derivative of is the same type of operation as to evaluate
the time derivative of the group velocity, our starting point here.
To perform this operation, we consider the variation of

k with time, i.e.
_
d
dt
_
=
_
_
3

j=1

k
j
dk
j
dt
_
_
Inserting this paranthesis in the previous equation, we obtain
dv
i
dt
=
1
h

k
i
_
_
3

j=1

k
j
dk
j
dt
_
_
Replacing the dk
j
/dt by F
j
/ h, we obtain
dv
i
dt
=
1
h
2
3

j=1

k
i
k
j
F
j
Inverted mass tensor
a =
_
1
m

_
F
Inverted mass components
a
i
=

j
_
1
m

_
i,j
F
j
As partial derivative
_
1
m

_
i,j
=

h

(k)
k
i
k
j
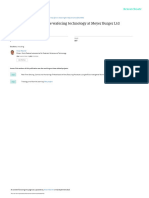
5. Illustrations of the Eective Mass
In the discussion of 3-dimensional bands a very simple expression has been
shown to model the structure of the bands, using the trigonometric functions.
The following gure illustrates how we can understand the behaviour of the
eective mass at the various positions in the band.
The eective mass can be used to describe the density of states in the band.
1 0.5 0 0.5 1
0
1
2
3
4
5
6
ka/
(a) Band E
b
= 3 2 cos(ka)
1 0.5 0 0.5 1
3
2
1
0
1
2
3
(b) Velocity v
g
= 2 sin(k)
ka/
1 0.5 0 0.5 1
3
2
1
0
1
2
3
ka/
(c) Inverse eff.m. 1/m* = 2 cos(k)
1 0.5 0 0.5 1
3
2
1
0
1
2
3
ka/
(d) Effective mass m*
Figure 5: An analytic model for a band - and the concepts of group velocity
and eective mass. The meaning of innite and negative eective mass can be
understood from here, consulting also the previous gure. Note that not the
eective mass itself, but its inverse 1/m

, is shown.
One can use a formula analogous to that one used for the Fermi gas
g() =
V
2
2
_
2m

h
2
_
3
2
|
b
|
1
2
where
b
is the minimal or maximal enrgy in the band. Give a short qualitative
description of how does the local density of states depend on the shape of the
band (as a function of the wavenumber) and how this can be related to the
eective mass. Compare qualitatively a narrow and a broad band, considering
the density of states as seen from the shape of the k diagram and as seen
from the above formula.
The numerical values of the eective mass can even become negative or innite.
The physical meaning can be understood from gure 5.
The eective mass is innite in the region where the dispersion relation means
LOCALLY NO DISPERSION (locally linear proportionality).
Thus, eectively local PHASE VELOCITY = GROUP VELOCITY
nondispersive waves <=> innite eective mass