Professional Documents
Culture Documents
OFDM Basics
Uploaded by
Karthik Mohan KCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
OFDM Basics
Uploaded by
Karthik Mohan KCopyright:
Available Formats
OFDM Based WLAN Systems
Muhammad Imadur Rahman, Suvra Sekhar Das,
Frank H.P. Fitzek
Center for TeleInFrastruktur (CTiF), Aalborg University
Neils Jernes Vej 12, 9220 Aalborg st, Denmark
phone: +45 9635 8688; e-mail: {imr,ssd,}@kom.aau.dk
18 February 2005
Technical Report R-04-1002; v1.2
ISBN 87-90834-43-7
ISSN 0908-1224
c
Aalborg University 2004
Abstract
This report is intended to provide an overview of the present state of WLANs with respect to
physical layer issues and identify some key research issues for future generations of WLANs. The
current standards (IEEE 802.11a in USA, HiperLAN/2 in Europe and MMAC in Japan) are all
based on OFDM in their PHY layer. Thus, detailed attention on basics of OFDM related WLAN
systems are given in the report. This is to introduce the existing techniques that are proposed or
implemented in dierent OFDM based WLANs. A special attention is given on synchronization
and channel estimation issues in WLAN due to the fact that virtually it is impossible to obtain
a reasonable quality of service without perfect (or near perfect or ecient) synchronization and
channel estimation. At the end of the report, some interesting topics that need to be studied in
the development of future generation wireless systems based on OFDM are presented.
It is worth mentioning here that the explanation on various topics presented here are in no
way a complete description. For details, it is suggested to study the references that are mentioned
in this report.
Preface
Science is a wonderful thing if one does not have to earn ones living at it.
-Albert Einstein
This report is an overview of Orthogonal Frequency Division Multiplexing(OFDM). It is an
outcome of the literature survey in the initial phase of our PhD studies under the Department
of Communications Technology of Aalborg University. The main focus of our PhD program is
OFDM for broadband mobile wireless communications.
The scope of the report is limited to a survey of the OFDM eld, establishment of its analytical
description and to list the challenges and areas of research. It does not intend to provide any
solution to the problems listed. This document is targeted for use as a rst hand guide to OFDM
fundamentals, to explore the activities around OFDM till to date, and to survey the potential
research areas involving OFDM implementation towards the next generation communication
systems.
We owe great thanks to Prof. Ramjee Prasad and Assoc. Prof. Ole Olsen for their caring
guidance and kind co-operation in helping us prepare this report. This work was partially
supported by Samsung, Korea under the JADE project framework in our research group. We
highly appreciate their support in this regard.
As we progress with the PhD studies in Aalborg, we intend to improve upon this report with
our increasing knowledge and competencies in OFDM based wireless systems.
Should this report have any factual error or typo mistakes, or should you have any suggestion
on how to improve the contents or writing style, you are always welcome to contact the authors.
Muhammad Imadur Rahman & Suvra Sekhar Das
Aalborg University, Denmark
22 January 2004
c
Aalborg University 2004 Technical Report: R-04-1002 Page i
Document History
date changes author/responsible
September 9, 2003 Initiation of the document Muhammad Imadur Rahman &
Suvra Sekhar Das
January 22, 2004 Version 1.0: Submission of rst draft Muhammad Imadur Rahman, Su-
vra Sekhar Das & Frank H.P.
Fitzek
March 31, 2004 Version 1.1: New format Muhammad Imadur Rahman &
Suvra Sekhar Das
18 February, 2005 Version 1.2: Chapter 4 is included Muhammad Imadur Rahman
c
Aalborg University 2004 Technical Report: R-04-1002 Page ii
Contents
Table of Contents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv
List of Figures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . v
List of Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vi
Abbreviations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vii
1 Introduction 1
1.1 Scope of the Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Organization of the Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2 Channel Impairments and MCM 4
2.1 Multipath Scenario . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2 Doppler Eect . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3 Shadow Fading or Shadowing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.4 Propagation Path Loss . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.5 Time Dispersion and Frequency Selective Fading . . . . . . . . . . . . . . . . . . 6
2.6 The Benet of Using Multicarrier Transmission . . . . . . . . . . . . . . . . . . . 6
3 OFDM Fundamentals 9
3.1 History and Development of OFDM . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.2 OFDM Transceiver Systems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.3 Channel Coding and Interleaving . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.4 Advantages of OFDM System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.4.1 Combating ISI and Reducing ICI . . . . . . . . . . . . . . . . . . . . . . . 13
3.4.2 Spectral Eciency . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.4.3 Some Other Benets of OFDM System . . . . . . . . . . . . . . . . . . . 15
3.5 Disadvantages of OFDM System . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.5.1 Strict Synchronization Requirement . . . . . . . . . . . . . . . . . . . . . 16
3.5.2 Peak-to-Average Power Ratio(PAPR) . . . . . . . . . . . . . . . . . . . . 16
3.5.3 Co-Channel Interference in Cellular OFDM . . . . . . . . . . . . . . . . . 17
3.6 OFDM System Design Issues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.6.1 OFDM System Design Requirements . . . . . . . . . . . . . . . . . . . . . 17
3.6.2 OFDM System Design Parameters . . . . . . . . . . . . . . . . . . . . . . 18
4 OFDM System Model 19
4.1 System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
4.2 Analytical model of OFDM System . . . . . . . . . . . . . . . . . . . . . . . . . . 21
4.2.1 Transmitter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
c
Aalborg University 2004 Technical Report: R-04-1002 Page iii
4.2.2 Channel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
4.2.3 Receiver . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
4.2.4 Sampling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
4.3 Single OFDM Symbol Baseband Model in Matrix Notations . . . . . . . . . . . . 26
5 Multi-Antenna OFDM Systems 29
5.1 Antenna Diversity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
5.1.1 Receiver Diversity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
5.1.2 Transmitter Diversity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
5.1.3 Cyclic Delay Diversity in OFDM Receiver . . . . . . . . . . . . . . . . . . 32
5.2 MIMO Techniques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
5.2.1 Spatial Multiplexing Algorithms . . . . . . . . . . . . . . . . . . . . . . . 34
5.2.2 Space-Time Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
5.2.3 Space-Frequency Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
6 Synchronization Issues 38
6.1 Symbol Timing Synchronization . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
6.2 Sampling Clock Synchronization . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
6.3 Carrier Frequency Synchronization . . . . . . . . . . . . . . . . . . . . . . . . . . 41
7 Channel Estimation 43
7.1 Exploiting Channel Correlation Properties for CSI Estimation . . . . . . . . . . . 43
7.2 Channel Estimation Based on Pilots . . . . . . . . . . . . . . . . . . . . . . . . . 44
7.2.1 Design of Pilot Based Channel Estimator . . . . . . . . . . . . . . . . . . 46
7.3 Channel Estimation Based on Training Symbols . . . . . . . . . . . . . . . . . . . 46
7.4 Blind Channel Estimation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
7.5 Channel Estimation in CDD-OFDM System . . . . . . . . . . . . . . . . . . . . . 47
7.6 Channel Estimation in MIMO Enhanced OFDM Systems . . . . . . . . . . . . . 48
8 Research Challenges 50
8.1 Wireless Channel Modelling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.2 Synchronization Issues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
8.3 Channel Estimation Issues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
8.4 Capacity Enhancement via MIMO . . . . . . . . . . . . . . . . . . . . . . . . . . 52
8.5 System Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
8.6 Peak to Average Power Reduction . . . . . . . . . . . . . . . . . . . . . . . . . . 53
8.7 Dynamic CP Length . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
8.8 OFDM Based Multi-User Systems . . . . . . . . . . . . . . . . . . . . . . . . . . 54
8.9 Miscellaneous Research Directions . . . . . . . . . . . . . . . . . . . . . . . . . . 55
9 Conclusion 56
Reference 56
c
Aalborg University 2004 Technical Report: R-04-1002 Page iv
List of Figures
2.1 Channel Impulse Responses and Corresponding Frequency Response . . . . . . . 5
2.2 Single Carrier Vs Multicarrier Approach . . . . . . . . . . . . . . . . . . . . . . . 7
3.1 OFDM Transceiver Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
3.2 Role of Guard Intervals and Cyclic Prex in Combatting ISI and ICI . . . . . . . 14
3.3 Spectrum Eciency of OFDM Compared to Conventional FDM . . . . . . . . . 15
4.1 Generic OFDM system downlink diagram . . . . . . . . . . . . . . . . . . . . . . 20
4.2 OFDM System model - Transmitter . . . . . . . . . . . . . . . . . . . . . . . . . 22
4.3 OFDM System model - Channel . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
4.4 OFDM System model - Receiver . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
4.5 Single OFDM Symbol System Model . . . . . . . . . . . . . . . . . . . . . . . . . 27
4.6 Simplied Single OFDM Symbol System Model . . . . . . . . . . . . . . . . . . . 28
5.1 Multiple Antenna Receiver Diversity with MRC at subcarrier level . . . . . . . . 30
5.2 OFDM Transmitter with CDD; Cyclic shifts introduced in the original signal are
xed. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
5.3 OFDM receiver with Pre-DFT Combining CDD. The instantaneous channel is
estimated from the received signals to determine the optimum cyclic shifts (and
gain factors, if MARC combining is performed). . . . . . . . . . . . . . . . . . . . 33
5.4 OFDM Based Spatial Multiplexing . . . . . . . . . . . . . . . . . . . . . . . . . . 34
5.5 Alamoutis Space-Time Block Coding Scheme . . . . . . . . . . . . . . . . . . . . 35
5.6 Space-Time OFDM System with STBC Algorithm . . . . . . . . . . . . . . . . . 36
6.1 Synchronization Error in any OFDM System . . . . . . . . . . . . . . . . . . . . 39
6.2 OFDM Preamble Structure Specied in IEEE 802.11a Standard . . . . . . . . . . 40
7.1 OFDM Receiver with Coherent Detection (using Channel Estimation) . . . . . . 44
7.2 Channel Estimation with Pilot Symbols . . . . . . . . . . . . . . . . . . . . . . . 45
7.3 An Example of Pilot Symbol Insertion Method . . . . . . . . . . . . . . . . . . . 46
c
Aalborg University 2004 Technical Report: R-04-1002 Page v
List of Tables
2.1 Comparison of Single Carrier and Multicarrier Approach in terms of Channel
Frequency Selectivity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.1 IEEE 802.11a OFDM PHY Modulation Techniques . . . . . . . . . . . . . . . . . 13
c
Aalborg University 2004 Technical Report: R-04-1002 Page vi
Abbreviations
2G 2
nd
Generation
3G 3
rd
Generation
4G 4
th
Generation
ADC Analog-to-Digital Converter
ADSL Asymmetric Digital Subscriber Lines
ASC Antenna Selection Combining
BPSK Binary Phase Shift Keying
CCK Complementary Code Keying
CDD Cyclic Delay Diversity
COFDM Coded Orthogonal Frequency Division Multiplexing
CP Cyclic Prex
CSI Channel State Information
DA Data Aided Algorithms
DAB Digital Audio Broadcasting
DAC Digital-to-Analog Converter
DBLAST Diagonal Bell Labs LAyered Space-Time
DFT Discrete Fourier Tranform
DVB Digital Video Broadcasting
DVB-T Digital Video Broadcasting - Terrestrial
DSSS Direct Sequence Spread Spectrum
EGC Equal Gain Combining
FEC Forward Error Correction
FFT Fast Fourier Transform
FHSS Frequency Hopping Spread Spectrum
FM Frequency Modulation
HDSL High-bit-rate Digital Subscriber Lines
HDTV High Denition TeleVision
HiperLAN High Performance Radio Local Area Networks
ICI Inter Carrier Interference
IDFT Inverse Discrete Fourier Transform
IFFT Inverse Fast Fourier Transform
IR Infra Red
ISI Inter Symbol Interference
LOS Line-Of-Sight
LS Least Squared
LMMSE Linear Minimum Mean Squared Error
c
Aalborg University 2004 Technical Report: R-04-1002 Page vii
MAN Metropolitan Area Networks
MARC Maximum Average (Signal-to-Noise) Ratio Combining
MIMO Multiple Input Multiple Output
MMAC Multimedia Mobile Access Communications Systems
MMSE Minimum Mean Squared Error
MRC Maximum Ratio Combining
MRRC Maximum Ratio Receiver Combining
MSE Mean Squared Error
MW Millimeter Wave
NDA Non Data-Aided Algorithms
NLOS Non Line-Of-Sight
OFDM Orthogonal Frequency Division Multiplexing
PAPR Peak-to-Average Power Ratio
PBCC Packet Binary Convolutional Coding
QAM Quadrature Amplitude Modulation
QoS Quality of Service
QPSK Quadrature Phase Shift Keying
RF Radio Frequency
RMS Root-Mean-Square
SC Selection Combining
SM Spatial Multiplexing
SNR Signal-to-Noise Ratio
SSC Subcarrier Selection Combining
STC Space-Time Coding
VBLAST Vertical Bell Labs LAyered Space-Time
VDSL Very-high-speed Digital Subscriber Lines
VoWIP Voice over Wireless Internet Protocol
WLAN Wireless Local Area Networks
W-OFDM Wideband Orthogonal Frequency Division Multiplexing
c
Aalborg University 2004 Technical Report: R-04-1002 Page viii
Chapter 1
Introduction
Wireless communication has gained a momentum in the last decade of 20
th
century with the
success of 2
nd
Generations (2G) of digital cellular mobile services. Worldwide successes of GSM,
IS-95, PDC, IS-54/137 etc. systems have shown new way of life for the new information and
communication technology era. These systems were derived from a voice legacy, thus primary
services were all voice transmission. 2G systems provided better quality of services at lower
cost and a better connectivity compared to previous analog cellular systems. Numerous market
researches show that there is a huge demand for high-speed mobile multimedia services all over
the world. With the advent of 3
rd
Generation (3G) wireless systems, it is expected that higher
mobility with reasonable data rate (up to 2Mbps) can be provided to meet the current user needs.
But, 3G is not the end of the tunnel, ever increasing user demands have drawn the industry to
search for better solutions to support data rates of the range of tens of Mbps. Naturally dealing
with ever unpredictable wireless channel at high data rate communications is not an easy task.
Hostile wireless channel has always been proved as a bottleneck for high speed wireless systems.
This motivated the researchers towards nding a better solution for combating all the odds of
wireless channels; thus, the idea of multi-carrier transmission has surfaced recently to be used
for future generations of wireless systems.
3G promises a wire line quality of services via a wireless channel. For wide area coverage,
further expansions of 3G systems are already a question of research in all over the world. Cer-
tainly the bit rate will be much higher than 2Mbps for such a system, up to tens of Mbps.
For local area coverage, Wireless Local Area Networks (WLANs), such as IEEE 802.11a, Hiper-
LAN/2 or MMAC
1
standards are capable of providing data rates up to 54 Mbps. Along with
these three, there are few other emerging short-range wireless applications available, such as
Bluetooth, HomeRF, etc.
WLANs can potentially be a promising tool in dierent user environments, namely home,
corporate and public environment etc. WLANs are used to connect wireless users to a xed LAN
in corporate environments. A major WLAN application will be in public sectors, where WLAN
can be used to connect a user to the backbone network. Airports, hotels, high-rising oces,
city centers will be target area for such public WLAN usage. It is becoming more and more
evident that WLANs will play a greater role in future. A popular vision of future generations of
telecommunications systems suggests that it will be an amalgamation of high data-rate wireless
wide area networks (such as UMTS) and newly standardized WLANs. However systems of the
1
IEEE802.11a is an USA-standard, HiperLAN/2 is a European standard and MMAC is developed in Japan.
All three of the standards are almost similar in their PHY layer.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 1
near future will require WLANs with data rate of greater than 100 Mbps, and so there is a need
to further improve the capacity of existing WLAN systems. Although the term 4G is not yet
clear to the industry, it is likely that they will enhance the 3G networks in capacity, allowing
greater range of applications and better universal access. Some of the visionaries term the system
as Mobile Broadband Services (MBS). A seamless and uninterrupted service quality for a user
regardless of the system he/she is using will be one of the main goals of future systems. The
expected systems will require an extensive amount of bandwidth per user.
Several technologies are considered to be candidates for future applications. According to
many, Wireless Personal Area Networks (WPAN) will be a major application of future wireless
communications [1]. WPAN will enable a kind of ubiquitous communications, that is, WPAN
will provide a continuous network connection to the user. This will revolutionize the future
home, where wireless communications appliances will be an integral part of home life. A user
can communicate through his networked WPAN that includes various communication-enabled
devices and can seamlessly move or address another user or WPAN nearby, through WPAN-
WPAN connections or through some backbone networks or WLAN. WPANs will be very similar
to WLANs in terms of operation, application and implementation, thus OFDM will be vividly
present in all future wireless devices as it appears now.
Orthogonal Frequency Division Multiplexing (OFDM) is a special form of multi-carrier trans-
mission where all the subcarriers are orthogonal to each other. OFDM promises a higher user
data rate and great resilience to severe signal fading eects of the wireless channel at a reasonable
level of implementation complexity. It has been taken as the primary physical layer technology
in high data rate Wireless LAN/MAN standards. IEEE 802.11a and HiperLAN/2 have the ca-
pability to operate in a range of a few tens of meters in typical oce space environment. IEEE
802.16a uses Wideband OFDM (W-OFDM) a patented technology of Wi-LAN to server up to 1
km radius of high data rate xed wireless connectivity. In the upcoming standard IEEE 802.20,
which is targeted at achieving data rate of greater than 1 Mbps at 250 kmph, OFDM is one
of the potential candidate. Thus we see that there is a strong possibility that next generation
wireless era belongs to OFDM technology.
1.1 Scope of the Report
This report attempts to connect the dierent strings of OFDM and create a comprehensive
reference. We attempt to provide an understanding of OFDM system along with a description
of the challenges and research areas for enhancing system capacity and improving link quality.
1.2 Organization of the Report
The rest of this report is organized as follows.
In Chapter 2, we talk about the wireless channel impairments that are encountered in de-
signing a communication system. It covers multipath interference, doppler eect, shadow fading,
propagation path loss, time and frequency selective fading and nally it includes the benet of
using Multi-carrier modulation technique to overcome the channel impairments.
In Chapter 3, we rst introduce the reader to the history and evolution of OFDM. It then
covers the components of an OFDM transceiver one by one. The chapter ends with a discussion of
the the advantages and disadvantages of OFDM systems. It is explained how OFDM deals with
c
Aalborg University 2004 Technical Report: R-04-1002 Page 2
ISI/ICI and how OFDM provides in spectral eciency. Synchronization, PAPR and co-channel
interference issues are also introduced in this chapter.
In Chapter 4, we build an analytical model of OFDM system based on the basics obtained
in the previous chapter. Mainly we have explained the system ow in analytical expressions to
have a better understanding of the scheme. At the end of the chapter, we have also included
a simple matrix model of the system in co-operation with analytical model. The matrix model
will give a better understanding, in case there is a need to prepare a simulation model in certain
programming environment, such as MATLAB.
Chapter 5 deals with diversity issues. We introduced how MIMO techniques can be incorpo-
rated with OFDM systems to signicantly improve the capacity and link quality of the system.
In Chapter 6, we discuss the synchronization issues in detail. It covers carrier frequency
synchronization, symbol timing and sampling clock synchronization.
In Chapter 7, we deal with channel estimation techniques, and explain three methods of
estimation, which are pilot based, training symbol based and blind channel estimation.
Chapter 8 briey identies a number of key research issues related to the development of
OFDM wireless system aimed at high data rate and vehicular mobility.
Finally Chapter 9 concludes the report.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 3
Chapter 2
Channel Impairments and MCM
Wireless channel is always very unpredictable with harsh and challenging propagation situations.
Wireless channel is very dierent from wire line channel in a lot of ways. Multipath reception is
the unique characteristic of wireless channels. Together with multipath, there are other serious
impairments present at the channel, namely propagation path loss, shadow fading, Doppler
spread, time dispersion or delay spread, etc.
2.1 Multipath Scenario
Multipath is the result of reection of wireless signals by objects in the environment between
the transmitter and receiver. The objects can be anything present on the signal travelling path,
i.e. buildings, trees, vehicles, hills or even human beings. Thus, multipath scenario includes
random number of received signal from the same transmission source; depending on the location
of transmitter and receiver, a direct transmission path referred to as the Line-Of-Sight (LOS)
path may be present or may not be present. When LOS component is present (or when one
of the components is much stronger than others), then the environment is modelled as Ricean
channel, and when no LOS signal is present, the environment is described as Rayleigh channel.
Multipaths arrive at the receiver with random phase osets, because each reected wave
follows a dierent path from transmitter to reach the receiver. The reected waves interfere
with direct LOS wave, which causes a severe degradation of network performance. The resultant
is random signal fades as the reections destructively (and/or constructively) superimpose one
another, which eectively cancels part of signal energy for a brief period of time. The severity of
fading will depend on delay spread of the reected signal, as embodied by their relative phases
and their relative power [2].
A common approach to represent the multipath channel is channel impulse response which
gives us the delay spread of the channel. Delay spread is the time spread between the arrival of
the rst and last multipath signal seen by receiver. In a digital system, delay spread can lead
to ISI. In Figure 2.1, delay spread amounts to
max
. It is noted that delay spread is always
measured with respect to the rst arriving component.
Lets assume a system transmitting in the time intervals T
sym
. The longest path with respect
to the earliest path arrives at the receiver with a delay of
max
; in other words, the last path arrives
max
seconds after the rst path arrives. This means that a received symbol can theoretically be
inuenced by previous symbols, which is termed as ISI. With high data rate, T
sym
can be very
small; thus the number of symbols that are aected by ISI can be in multiple of tens or more.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 4
Channel Response in Time
Max delay spread,
max
Channel Response in Frequency
(Frequency Selectivity)
Time
Frequency
H(f)
f
h( )
Figure 2.1: Channel Impulse Responses and Corresponding Frequency Response
Combating the inuence of such large ISI at the receiver is very challenging and sometimes may
become unattainable at very severe channel conditions [3].
2.2 Doppler Eect
Doppler spread is caused by the relative motion of transmitter and receiver. For example, in an
urban environment in the city center, the vehicles are always moving; the walking pedestrians are
also changing their locations continuously, thus their movements aect the transmission medium.
A high Doppler can be experienced when a user is located in a fast moving car or in a speedy
train, because the relative motion will be higher when either transmitter or receiver is moving
very fast. This relative motion of transmitter and receiver changes the received signal from
the original transmitted signal. When they are moving towards each other, the frequency of
the received signal is higher than the source and when they moving away from each other, the
received frequency decreases. When the relative speed is higher, then Doppler shift can be very
high, and thus the receiver may become unable to detect the transmitted signal frequency. Even
at lower relative motion when the Doppler shift is usually very little, if the transmission and
reception technique is very sensitive to carrier frequency oset, then the system may fail.
2.3 Shadow Fading or Shadowing
Shadow fading is another troublesome eect of wireless channel. Wireless signals are obstructed
by large obstacles, like huge buildings, high hills, etc. These large objects cause reections o
their surface and attenuation of signals passing through them, resulting in shadowing, or shadow
fading. These shadows can result in large areas with high path loss, causing problems with
communications. The amount of shadowing depends on the size of the object, the structure of
the material, and the frequency of the RF signal. Large attenuations by huge obstacles can result
in deep fading behind them. Under this condition, most of the received signal energy comes from
reected and diracted paths of the original signal, because LOS is absent due to large object
between the transmitter and the receiver.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 5
2.4 Propagation Path Loss
Together with multipath eect, shadowing and Doppler spread, the propagation loss is also very
signicant at some specic situation. The propagation loss increases by fourth power of distance
[4]. So, for higher distances, propagation loss becomes signicant. Well dened situation specic
path loss models are available to estimate the propagation path loss.
2.5 Time Dispersion and Frequency Selective Fading
Time dispersion represents distortion of the signal that is manifested by the spreading of the
modulation symbols in time domain. We all know that channel is mostly band-limited in case
of broadband multimedia communications, i.e. the coherence bandwidth of the channel is al-
ways smaller than modulation bandwidth. So ISI is unavoidable in wireless channels. In many
instances, fading by the multipath will be frequency selective. This implies that signals will
be aected only at part of the available frequency band. The eect has a random pattern for
any given time. At certain frequencies, it will be enhanced (constructive interference) and will
be completely (or partially) suppressed at other frequencies. Frequency selective fading occurs
when channel introduces time dispersion and the delay spread is larger than the symbol period.
Frequency selective fading is dicult to compensate because the fading characteristics is random
and sometimes may not be easily predictable. When there is no dispersion and the delay spread is
less than the symbol period, the fading will be at, thereby aecting all frequencies in the signal
equally. Practically at fading is easily estimated and compensated with a simple equalization
[2].
2.6 The Benet of Using Multicarrier Transmission
A single carrier system suers from trivial ISI problem when data rate is extremely high. We
need high data rate to support wireless broadband applications, thus these applications always
suer from ISI. According to previous discussions, we have seen that with a bandwidth B and
symbol duration T
sym
, when
max
> T
sym
, then ISI occurs. Multichannel transmission has been
surfaced to solve this problem. The idea is to increase the symbol period of subchannels by
reducing the data rate and thus reducing the eect of ISI. Reducing the eect of ISI yields an
easier equalization, which in turn means simpler reception techniques.
Wireless multimedia solutions require up to tens of Mbps for a reasonable quality of service.
If we consider single carrier high speed wireless data transmission, we see that the delay spread at
such high data rate will denitely be greater than symbol duration even considering the best case
outdoor scenario. Now, if we divide the high data rate channel over number of subcarriers, then
we have larger symbol duration in the subcarriers and maximum delay spread is much smaller
than the symbol duration.
Figure 2.2 describes this very eciently [5]. Lets assume that we have available bandwidth
B of 1MHz. Now in a single carrier approach, we transmit the data at symbol duration of 1s.
Consider a typical outdoor scenario where maximum delay spread can be 10s, so at the worst
case scenario, at least 10 symbols will be aected by each and every symbol. Thus, ISI eect of
every symbol will be spread to 10 successive symbols.
In a single carrier system, this situation is compensated by using adaptive equalization tech-
nique. Adaptive equalization estimates the channel impulse response and multiplies complex
c
Aalborg University 2004 Technical Report: R-04-1002 Page 6
Time
Frequency
T = 1/B = 1s
symbol
B
=
1
M
H
z
Time
Frequency
T = 1/B = 1ms
symbol
B
=
1
M
H
z
f
=
1
K
H
z
a)
Complex equalizer is needed
to reduce severe ISI
Single carrier approach:
a)
Available bandwidth is divided
into subchannels; each symbol
occupies a narrow band but
longer time period
Multicarrier approach:
N
Number of subcarriers = 1000
Figure 2.2: Single Carrier Vs Multicarrier Approach
Design Parameters
for outdoor channel
Required data rate 1Mbps
RMS delay spread, 10s
Channel coherence bandwidth, B
c
=
1
5
20KHz
Frequency selectivity condition >
T
sym
10
Single carrier
approach
Symbol duration, T
sym
1s
Frequency selectivity 10s >
1s
10
= YES
ISI occurs as the channel is frequency selective
Multicarrier
approach
Total number of subcarriers 128
Data rate per subcarrier 7.8125kbps
Symbol duration per subcarrier T
carr
= 128s
Frequency selectivity 10s >
128s
10
= NO
ISI is reduced as at fading occurs.
CP completely removes the remaining ISI
Table 2.1: Comparison of Single Carrier and Multicarrier Approach in terms of Channel Fre-
quency Selectivity
c
Aalborg University 2004 Technical Report: R-04-1002 Page 7
conjugate of the estimated impulse response with the received data signal at the receiver. How-
ever, there are some practical computational diculties in performing these equalization tech-
niques at tens of Mbps with compact and low cost hardware. It is worth mentioning here that
compact and low cost hardware devices do not necessarily function at very high data speed. In
fact, equalization procedures take bulk of receiver resources, costing high computation power
and thus overall service and hardware cost becomes higher. Complex receivers are very ecient
in performance, but not cost ecient.
One way to achieve reasonable quality and solve the problems described above for broadband
mobile communication is to use parallel transmission. In a crude sense, someone can say in prin-
ciple that parallel transmission is just the summation of a number of single carrier transmissions
at the adjacent frequencies. The dierence is that the channels have lower data transmission rate
than the original single carrier system and the low rate streams are orthogonal to each other. If
we consider a multi-carrier approach where we have N number of subcarriers, we can see that
we can have
B
N
Hz of bandwidth per subcarrier. If N = 1000 and B = 1MHz, then we have
subcarrier bandwidth B
carr
of 1kHz. Thus, symbol duration in each subcarrier will be increased
to 1ms (=
1
1kHz
). Here each symbol occupies a narrow band but longer time period. This clearly
shows that maximum delay spread of 1 msec will not have any ISI eects on received symbols
in the outdoor scenario mentioned above. In another thought, multi-carrier approach turns the
channel to a at fading channel and thus can easily be estimated.
Theoretically increasing the number of subcarriers should be able to give better performance
in a sense that we will able to handle larger delay spreads. But several typical implementation
problems arise with large number of subcarriers. When we have large numbers of subcarriers,
then we will have to assign the subcarriers frequencies very close to each other. We know that
receiver needs to synchronize itself to every subcarrier frequency in order to recover data related
to that particular subcarrier. When spacing is very little, then the receiver synchronization
components need to be very accurate, which is still not possible with low-cost RF hardware.
Thus, a reasonable trade-o between carrier spacing and number of subcarriers must be achieved.
Table 2.1 describes how multicarrier approach can convert the channel to at fading channel
from frequency selective fading channel. We have considered a multicarrier system with a single
carrier system, where the system data rate requirement is 1Mbps. When we use 128 subcarriers
for multicarrier system, we can see that the ISI problem is clearly solved. It is obvious that if
we increase the number of subcarriers, the system will provide even better performance.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 8
Chapter 3
OFDM Fundamentals
The nature of WLAN applications demands high data rates. Naturally dealing with ever-
unpredictable wireless channel at high data rate communications is not an easy task. The idea of
multi-carrier transmission has surfaced recently to be used for combating the hostility of wireless
channel as high data rate communications. OFDM is a special form of multi-carrier transmission
where all the subcarriers are orthogonal to each other. OFDM promises a higher user data rate
transmission capability at a reasonable complexity and precision.
At high data rates, the channel distortion to the data is very signicant, and it is some-
what impossible to recover the transmitted data with a simple receiver. A very complex receiver
structure is needed which makes use of computationally extensive equalization and channel es-
timation algorithms to correctly estimate the channel, so that the estimations can be used with
the received data to recover the originally transmitted data. OFDM can drastically simplify
the equalization problem by turning the frequency selective channel to a at channel. A simple
one-tap equalizer is needed to estimate the channel and recover the data.
Future telecommunication systems must be spectrally ecient to support a number of high
data rate users. OFDM uses the available spectrum very eciently which is very useful for
multimedia communications. Thus, OFDM stands a good chance to become the prime technology
for 4G. Pure OFDM or hybrid OFDM will be most likely the choice for physical layer multiple
access technique in the future generation of telecommunications systems.
3.1 History and Development of OFDM
Although OFDM has only recently been gaining interest from telecommunications industry, it
had a long history of existence. It is reported that OFDM based systems were in existence
during the Second World War. OFDM had been used by US military in several high frequency
military systems such as KINEPLEX, ANDEFT and KATHRYN [6]. KATHRYN used AN/GSC-
10 variable rate data modem built for high frequency radio. Up to 34 parallel low rate channels
using PSK modulation were generated by a frequency multiplexed set of subchannels. Orthogonal
frequency assignment was used with channel spacing of 82Hz to provide guard time between
successive signaling elements [7].
In December 1966, Robert W. Chang
1
outlined a theoretical way to transmit simultaneous
data stream trough linear band limited channel without Inter Symbol Interference (ISI) and
1
Robert W. Chang, Synthesis of Band-limited Orthogonal Signals for Multichannel Data Transmission, The
Bell Systems Technical Journal, December 1966.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 9
Inter Carrier Interference (ICI). Subsequently, he obtained the rst US patent on OFDM in
1970 [8]. Around the same time, Saltzberg
2
performed an analysis of the performance of the
OFDM system. Until this time, we needed a large number of subcarrier oscillators to perform
parallel modulations and demodulations.
A major breakthrough in the history of OFDM came in 1971 when Weinstein and Ebert
3
used
Discrete Fourier Transform (DFT) to perform baseband modulation and demodulation focusing
on ecient processing. This eliminated the need for bank of subcarrier oscillators, thus paving
the way for easier, more useful and ecient implementation of the system.
All the proposals until this time used guard spaces in frequency domain and a raised cosine
windowing in time domain to combat ISI and ICI. Another milestone for OFDM history was
when Peled and Ruiz
4
introduced Cyclic Prex (CP) or cyclic extension in 1980. This solved the
problem of maintaining orthogonal characteristics of the transmitted signals at severe transmis-
sion conditions. The generic idea that they placed was to use cyclic extension of OFDM symbols
instead of using empty guard spaces in frequency domain. This eectively turns the channel as
performing cyclic convolution, which provides orthogonality over dispersive channels when CP
is longer than the channel impulse response [6]. It is obvious that introducing CP causes loss of
signal energy proportional to length of CP compared to symbol length, but, on the other hand,
it facilitates a zero ICI advantage which pays o.
By this time, inclusion of FFT and CP in OFDM system and substantial advancements in
Digital Signal Processing (DSP) technology made it an important part of telecommunications
landscape. In the 1990s, OFDM was exploited for wideband data communications over mobile
radio FM channels, High-bit-rate Digital Subscriber Lines (HDSL at 1.6Mbps), Asymmetric Dig-
ital Subscriber Lines (ADSL up to 6Mbps) and Very-high-speed Digital Subscriber Lines (VDSL
at 100Mbps).
Digital Audio Broadcasting (DAB) was the rst commercial use of OFDM technology. Devel-
opment of DAB started in 1987. By 1992, DAB was proposed and the standard was formulated
in 1994. DAB services came to reality in 1995 in UK and Sweden. The development of Digital
Video Broadcasting (DVB) was started in 1993. DVB along with High-Denition TeleVision
(HDTV) terrestrial broadcasting standard was published in 1995. At the dawn of the 20th cen-
tury, several Wireless Local Area Network (WLAN) standards adopted OFDM on their physical
layers. Development of European WLAN standard HiperLAN started in 1995. HiperLAN/2 was
dened in June 1999 which adopts OFDM in physical layer. Recently IEEE 802.11a in USA has
also adopted OFDM in their PHY layer.
Perhaps of even greater importance is the emergence of this technology as a competitor
for future 4th Generations (4G) wireless systems. These systems, expected to emerge by the
year 2010, promise to at last deliver on the wireless Nirvana of anywhere, anytime, anything
communications. Should OFDM gain prominence in this arena, and telecom giants are banking
on just this scenario, then OFDM will become the technology of choice in most wireless links
worldwide [9].
2
B. R. Saltzberg, Performance of an Ecient Parallel Data Transmission System, IEEE Transactions on
Communications, COM-15 (6), pp. 805-811, December 1967.
3
S. B. Weinstein, P. M. Ebert, Data Transmission of Frequency Division Multiplexing Using The Discrete
Frequency Transform, IEEE Transactions on Communications, COM-19(5), pp. 623-634, October 1971.
4
R. Peled & A. Ruiz, Frequency Domain Data Transmission Using Reduced Computational Complexity Algo-
rithms, in Proceeding of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP
80, pp. 964-967, Denver, USA, 1980.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 10
3.2 OFDM Transceiver Systems
A complete OFDM transceiver system is described in Figure 3.1. In this model, Forward Error
Control/Correction (FEC) coding and interleaving are added in the system to obtain the robust-
ness needed to protect against burst errors (see Section 3.3 for details). An OFDM system with
addition of channel coding and interleaving is referred to as Coded OFDM (COFDM).
In a digital domain, binary input data is collected and FEC coded with schemes such as
convolutional codes. The coded bit stream is interleaved to obtain diversity gain. Afterwards,
a group of channel coded bits are gathered together (1 for BPSK, 2 for QPSK, 4 for QPSK,
etc.) and mapped to corresponding constellation points. At this point, the data is represented
in complex numbers and they are in serial. Known pilot symbols mapped with known mapping
schemes can be inserted at this moment. A serial to parallel converter is applied and the IFFT
operation is performed on the parallel complex data. The transformed data is grouped together
again, as per the number of required transmission subcarriers. Cyclic prex is inserted in every
block of data according to the system specication and the data is multiplexed to a serial fashion.
At this point of time, the data is OFDM modulated and ready to be transmitted. A Digital-to-
Analog Converter (DAC) is used to transform the time domain digital data to time domain analog
data. RF modulation is performed and the signal is up-converted to transmission frequency.
After the transmission of OFDM signal from the transmitter antenna, the signals go through
all the anomaly and hostility of wireless channel. After the receiving the signal, the receiver down-
converts the signal; and converts to digital domain using Analog-to-Digital Converter (ADC). At
the time of down-conversion of received signal, carrier frequency synchronization is performed.
After ADC conversion, symbol timing synchronization is achieved. An FFT block is used to
demodulate the OFDM signal. After that, channel estimation is performed using the demodu-
lated pilots. Using the estimations, the complex received data is obtained which are demapped
according to the transmission constellation diagram. At this moment, FEC decoding and de-
interleaving are used to recover the originally transmitted bit stream.
3.3 Channel Coding and Interleaving
Since OFDM carriers are spread over a frequency range, there still may be some frequency
selective attenuation on a time varying basis. A deep fade on a particular frequency may cause
the loss of data on that frequency for that given time, thus some of the subcarriers can be
strongly attenuated and that will cause burst errors. In these situations, FEC in COFDM can
x the errors [10]. An ecient FEC coding in at fading situations leads to a very high coding
gain, especially if soft decision decoding is applied. In a single carrier modulation, if such a deep
fade occurs, too many consecutive symbols may be lost and FEC may not be too eective in
recovering the lost data [11].
Experiences show that basic OFDM system is not able to obtain a BER of 10
5
or 10
6
without channel coding. Thus, all OFDM systems now-a-days are converted to COFDM. The
benets of COFDM are two-fold in terms of performance improvement. First, the benet that
the channel coding brings in, that is the robustness to burst error. Secondly, interleaving brings
frequency diversity. The interleaver ensures that adjacent outputs from channel encoder are
placed far apart in frequency domain. Specically for a rate encoder, the channel encoder
provides two output bits for one source bit. When they are placed far apart from each other (i.e.
placed on subcarriers that are far from each other in frequency domain), then they experience
c
Aalborg University 2004 Technical Report: R-04-1002 Page 11
Error Correction
Coding and
Interleaving
Binary Input Data
Symbol Mapping
(data modulation)
Pilot symbol
insertion
Complex data
constellations
Serial -to- Parallel
OFDM Modulation
via IFFT
I Q
CP
I Q
DAC
I Q
I/Q Modulation
and up-conversion
Baseband
transmitted
signal
RF RF
Down conversion
and I/Q demodulation
Carrier
synchronization
ADC
Received signal
at Baseband
Q
I
Q
I
CP
Time
synchronization
OFDM demodulation
via IFFT
Q
I
Parallel-to-serial
Channel estimation
based on Pilot symbols
Symbol demapping
(data demodulation)
Received Complex
data constellations
Error Correction
decoding and
de-interleaving
Output binary data
Multipath Radio Channel
R
e
c
e
i
v
e
r
T
r
a
n
s
m
i
t
t
e
r
Analog signal
Digital signal
Figure 3.1: OFDM Transceiver Model
c
Aalborg University 2004 Technical Report: R-04-1002 Page 12
Data Modulation Coding Coded Code bits Data bits
rate scheme rate bits per per OFDM per OFDM
(Mbps) subcarrier symbol symbol
6 BPSK
1
2
1 48 24
9 BPSK
3
4
1 48 36
12 QPSK
1
2
2 96 48
18 QPSK
3
4
2 96 72
24 16-QAM
1
2
4 192 96
36 16-QAM
3
4
4 192 144
48 64-QAM
2
3
6 288 192
54 64-QAM
3
4
6 288 216
Table 3.1: IEEE 802.11a OFDM PHY Modulation Techniques
unique gain (and/or unique fade). It is very unlikely that both of the bits will face a deep fade,
and thus at least one of the bits will be received intact on the receiver side, and as a result,
overall BER performance will improve [9].
According to Table 3.1, IEEE 802.11a standard oers wide variety of choices for coding and
modulation, this allows a chance of making trade-os for lot of considerations. The standard
enables several data rates by making use of dierent combinations of modulation and channel
coding scheme. It is worth mentioning here that the standard demands all 802.11a complaint
products to support all the data rates. Table 3.1 presents the dierent arrangement of modulation
and coding scheme that are used to obtain the data rates [12].
3.4 Advantages of OFDM System
3.4.1 Combating ISI and Reducing ICI
When signal passes through a time-dispersive channel, the orthogonality of the signal can be
jeopardized. CP helps to maintain orthogonality between the sub carriers. Before CP was
invented, guard interval was proposed as the solution. Guard interval was dened by an empty
space between two OFDM symbols, which serves as a buer for the multipath reection. The
interval must be chosen as larger than the expected maximum delay spread, such that multi path
reection from one symbol would not interfere with another. In practice, the empty guard time
introduces ICI. ICI is crosstalk between dierent subcarriers, which means they are no longer
orthogonal to each other [6]. A better solution was later found, that is cyclic extension of OFDM
symbol or CP. CP is a copy of the last part of OFDM symbol which is appended to front the
transmitted OFDM symbol [13].
CP still occupies the same time interval as guard period, but it ensures that the delayed
replicas of the OFDM symbols will always have a complete symbol within the FFT interval
(often referred as FFT window); this makes the transmitted signal periodic. This periodicity
plays a very signicant role as this helps maintaining the orthogonality. The concept of being
able to do this, and what it means, comes from the nature of IFFT/FFT process. When the
IFFT is taken for a symbol period during OFDM modulation, the resulting time sample process
c
Aalborg University 2004 Technical Report: R-04-1002 Page 13
Data part of OFDM symbol
Using empty spaces as guard
interval at the beginning of
each symbol
Guard Interval, T >
CP max
t
Complete OFDM symbol
Next OFDM symbol
Complete OFDM symbol
Data part of OFDM symbol Next OFDM symbol
End of symbol is prepended to beginning
Guard interval still equals to T
CP Using cyclic prefix:
OFDM symbol length: T +
Efficiency:
sym
T
T / (T + T )
CP
sym sym CP
Figure 3.2: Role of Guard Intervals and Cyclic Prex in Combatting ISI and ICI
is technically periodic. In a Fourier transform, all the resultant components of the original signal
are orthogonal to each other. So, in short, by providing periodicity to the OFDM source signal,
CP makes sure that subsequent subcarriers are orthogonal to each other.
At the receiver side, CP is removed before any processing starts. As long as the length of CP
interval is larger than maximum expected delay spread
max
, all reections of previous symbols
are removed and orthogonality is restored. The orthogonality is lost when the delay spread is
larger than length of CP interval. Inserting CP has its own cost, we loose a part of signal energy
since it carries no information. The loss is measured as
SNR
loss CP
= 10 log
10
_
1
T
CP
T
sym
_
(3.1)
Here, T
CP
is the interval length of CP and T
sym
is the OFDM symbol duration. It is understood
that although we loose part of signal energy, the fact that zero ICI and ISI situation pay o the
loss.
To conclude, CP gives two fold advantages, rst occupying the guard interval, it removes the
eect of ISI and by maintaining orthogonality it completely removes the ICI. The cost in terms
signal energy loss is not too signicant.
3.4.2 Spectral Eciency
Figure 3.3 illustrates the dierent between conventional FDM and OFDM systems. In the case
of OFDM, a better spectral eciency is achieved by maintaining orthogonality between the sub-
carriers. When orthogonality is maintained between dierent subchannels during transmission,
then it is possible to separate the signals very easily at the receiver side. Classical FDM ensures
this by inserting guard bands between sub channels. These guard bands keep the subchannels
far enough so that separation of dierent subchannels are possible. Naturally inserting guard
bands results to inecient use of spectral resources.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 14
N=1
BW=2R
BW=2R
-R +R -R +R
BW=2R
-R +R
N=2
SC BW=R
BW=3R/2
-R +R
-3R/4 -R/4 R/4 +3R/4
BW=2R
-R +R
N=2
SC BW=2R/3
BW=4R/3
-R +R
-2R/3 -R/3 R/3 +2R/3 -R/3 R/3
Conventional FDM Orthogonal FDM
Figure 3.3: Spectrum Eciency of OFDM Compared to Conventional FDM
Orthogonality makes it possible in OFDM to arrange the subcarriers in such a way that
the sidebands of the individual carriers overlap and still the signals are received at the receiver
without being interfered by ICI. The receiver acts as a bank of demodulator, translating each
subcarrier down to DC, with the resulting signal integrated over a symbol period to recover raw
data. If the other subcarriers all down converted to the frequencies that, in the time domain,
have a whole number of cycles in a symbol period T
sym
, then the integration process results in
zero contribution from all other carriers. Thus, the subcarriers are linearly independent (i.e.,
orthogonal) if the carrier spacing is a multiple of
1
T
sym
[14].
3.4.3 Some Other Benets of OFDM System
1. The beauty of OFDM lies in its simplicity. One trick of the trade that makes OFDM
transmitters low cost is the ability to implement the mapping of bits to unique carriers via
the use of IFFT [9].
2. Unlike CDMA, OFDM receiver collects signal energy in frequency domain, thus it is able
to protect energy loss at frequency domain.
3. In a relatively slow time-varying channel, it is possible to signicantly enhance the capacity
by adapting the data rate per subcarrier according to SNR of that particular subcarrier
[6].
4. OFDM is more resistant to frequency selective fading than single carrier systems.
5. The OFDM transmitter simplies the channel eect, thus a simpler receiver structure is
enough for recovering transmitted data. If we use coherent modulation schemes, then very
simple channel estimation (and/or equalization) is needed, on the other hand, we need no
channel estimator if dierential modulation schemes are used.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 15
6. The orthogonality preservation procedures in OFDM are much simpler compared to CDMA
or TDMA techniques even in very severe multipath conditions.
7. It is possible to use maximum likelihood detection with reasonable complexity [10].
8. OFDM can be used for high-speed multimedia applications with lower service cost.
9. OFDM can support dynamic packet access.
10. Single frequency networks are possible in OFDM, which is especially attractive for broad-
cast applications.
11. Smart antennas can be integrated with OFDM. MIMO systems and space-time coding
can be realized on OFDM and all the benets of MIMO systems can be obtained easily.
Adaptive modulation and tone/power allocation are also realizable on OFDM.
3.5 Disadvantages of OFDM System
3.5.1 Strict Synchronization Requirement
OFDM is highly sensitive to time and frequency synchronization errors, especially at frequency
synchronization errors, everything can go wrong [15]. Demodulation of an OFDM signal with an
oset in the frequency can lead to a high bit error rate.
The source of synchronization errors are two; rst one being the dierence between local os-
cillator frequencies in transmitter and receiver, secondly relative motion between the transmitter
and receiver that gives Doppler spread. Local oscillator frequencies at both points must match
as closely as they can. For higher number of subchannels, the matching should be even more
perfect. Motion of transmitter and receiver causes the other frequency error. So, OFDM may
show signicant performance degradation at high-speed moving vehicles [8].
To optimize the performance of an OFDM link, accurate synchronization is a prime impor-
tance. Synchronization needs to be done in three factors: symbol, carrier frequency and sampling
frequency synchronization. A good description of synchronization procedures is given in [16]. We
have discussed the synchronization issues in detail in Section ??.
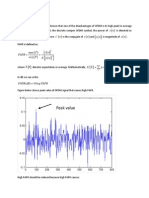
3.5.2 Peak-to-Average Power Ratio(PAPR)
Peak to Average Power Ratio (PAPR) is proportional to the number of sub-carriers used for
OFDM systems. An OFDM system with large number of sub-carriers will thus have a very
large PAPR when the sub-carriers add up coherently. Large PAPR of a system makes the
implementation of Digital-to-Analog Converter (DAC) and Analog-to-Digital Converter(ADC)
to be extremely dicult. The design of RF amplier also becomes increasingly dicult as the
PAPR increases.
There are basically three techniques that are used at present to reduce PAPR, they are Signal
Distortion Techniques, Coding Techniques and nally the Scrambling Technique. Since OFDM
is characterized by
x(t) =
1
N
N
n=1
a
n
e
jw
n
t
. (3.2)
c
Aalborg University 2004 Technical Report: R-04-1002 Page 16
Here a
n
is the modulating signal. For Large number of a
n
both the real and imaginary
parts tend to be Gaussian distributed, thus the amplitude of the OFDM symbol has a Rayleigh
distribution, while the power distribution is central chi squared.
The clipping and windowing technique reduces PAPR by non-linear distortion of the OFDM
signal. It thus introduces self interference as the maximum amplitude level is limited to a xed
level. It also increases the out of band radiation, but this is the simplest method to reduce
the PAPR. To reduce the error rate, additional Forward error correcting codes can be used in
conjunction with the the clipping and windowing method.
Another technique called Linear Peak Cancellation can also be used to reduce the PAPR.
In this method, time shifted and scaled reference function is subtracted from the signal, such
that each subtracted reference function reduces the peak power of at least one signal sample.
By selecting an appropriate reference function with approximately the same bandwidth as the
transmitted function, it can be assured that the peak power reduction does not cause out of band
interference. One example of a suitable reference function is a raised cosine window. Detailed
discussion about coding methods to reduce PAPR can be found in [6].
3.5.3 Co-Channel Interference in Cellular OFDM
In cellular communications systems, CCI is combated by combining adaptive antenna techniques,
such as sectorization, directive antenna, antenna arrays, etc. Using OFDM in cellular systems
will give rise to CCI. Similarly with the traditional techniques, with the aid of beam steering,
it is possible to focus the receivers antenna beam on the served user, while attenuating the
co-channel interferers. This is signicant since OFDM is sensitive to CCI.
3.6 OFDM System Design Issues
System design always needs a complete and comprehensive understanding and consideration of
critical parameters. OFDM system design is of no exception, it deals with some critical, and
often conicting parameters. Basic OFDM philosophy is to decrease data rate at the subcarriers,
so that the symbol duration increases, thus the multipaths are eectively removed. This poses
a challenging problem, as higher value for CP interval will give better result, but it will increase
the loss of energy due to insertion of CP. Thus, a tradeo between these two must be obtained
for a reasonable design.
3.6.1 OFDM System Design Requirements
OFDM systems depend on four system requirement:
Available bandwidth: Bandwidth is always the scarce resource, so the mother of the
system design should be the available for bandwidth for operation. The amount of band-
width will play a signicant role in determining number of subcarriers, because with a large
bandwidth, we can easily t in large number of subcarriers with reasonable guard space.
Required bit rate: The overall system should be able to support the data rate required
by the users. For example, to support broadband wireless multimedia communication, the
system should operate at more than 10 Mbps at least.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 17
Tolerable delay spread: Tolerable delay spread will depend on the user environment.
Measurements show that indoor environment experiences maximum delay spread of few
hundreds of nsec at most, whereas outdoor environment can experience up to 10s. So the
length of CP should be determined according to the tolerable delay spread.
Doppler values: Users on a high speed vehicle will experience higher Doppler shift where
as pedestrians will experience smaller Doppler shift. These considerations must be taken
into account.
3.6.2 OFDM System Design Parameters
The design parameters are derived according to the system requirements. The requirement of the
system design must be fullled by the system parameters. Following are the design parameters
for an OFDM system [6]:
Number of subcarriers: Increasing number of subcarriers will reduce the data rate via
each subcarrier, which will make sure that the relative amount of dispersion in time caused
by multipath delay will be decreased. But when there are large numbers of subcarriers,
the synchronization at the receiver side will be extremely dicult.
Guard time (CP interval) and symbol duration: A good ratio between the CP
interval and symbol duration should be found, so that all multipaths are resolved and
not signicant amount of energy is lost due to CP. As a thumb rule, the CP interval
must be two to four times larger than the Root-Mean-Square (RMS) delay spread. Symbol
duration should be much larger than the guard time to minimize the loss of SNR, but within
reasonable amount. It cannot be arbitrarily large, because larger symbol time means that
more subcarriers can t within the symbol time. More subcarriers increase the signal
processing load at both the transmitter and receiver, increasing the cost and complexity of
the resulting device [17].
Subcarrier spacing: Subcarrier spacing must be kept at a level so that synchronization
is achievable. This parameter will largely depend on available bandwidth and the required
number of subchannels.
Modulation type per subcarrier: This is trivial, because dierent modulation scheme
will give dierent performance. Adaptive modulation and bit loading may be needed de-
pending on the performance requirement. It is interesting to note that the performance of
OFDM systems with dierential modulation compares quite well with systems using non-
dierential and coherent demodulation [18]. Furthermore, the computation complexity in
the demodulation process is quite low for dierential modulations.
FEC coding: Choice of FEC code will play a vital role also. A suitable FEC coding will
make sure that the channel is robust to all the random errors.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 18
Chapter 4
OFDM System Model
In this chapter, an analytical model for OFDM scheme is presented. The rst section provides
the scope of the chapter, and presents an overview of a generic OFDM system. The subsystems of
interest to the modelling are then found. The second section contains an analytical time-domain
model for an OFDM system, disregarding the dierent multiple-access techniques, as we are here
focussing on the OFDM system as a basic transmission scheme. It should be fairly simple to
extend this model to multi-user scenario.
The analytical model that is explained in this chapter is taken from these authors another
work in [19].
4.1 System
In this deliverable, several OFDM-based multiple-access schemes are described in a downlink
(DL) scenario. In the DL scenario, the base station transmits a signal (containing data from
several users) to the dierent mobile stations. At the mobile station, only one user signal is
extracted. This is illustrated in Figure 4.1, where data streams from several users are transmitted
over the same OFDM carrier signal. The source bits from each user are source encoded, and then
digitally modulated (i.e. M bits are grouped and used to determine the constellation point). The
resource mapping combines the dierent user signals in a manner dependent on the multiple-
access scheme used, be it assigning dierent users to dierent subcarriers (as in OFDMA) or
using CDMA techniques (such as in MC-CDMA). Following the resource mapping, the resulting
subcarrier sequence is processed in the OFDM block, where the signal is converted from the
subcarrier domain to the time-domain and the cyclic prex (CP) is added. The signal is then
converted to a carrier frequency and transmitted over the channel.
In the receiver, the signal is down-converted and each OFDM symbol is processed, i.e. the
CP is removed and the signal is converted into the subcarrier domain. The OFDM block also
estimates the channel transfer function in order to compensate for fading. Following OFDM
processing, the user signals are separated and the signal for the u
th
user is extracted.
The functional block that are of interest in this chapter are boxed in Figure 4.1. The analytical
model presented in Section 4.2 only concerns the OFDM modulation/demodulation and the
channel, as this processing is common to any multiple-access schemes on top of basic OFDM
system.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 19
PSfrag replacements
Coding
Coding
Coding
Decoding
User 1
User 2
User u
User U
Mod
Mod
Mod
Demod
R
e
s
o
u
r
c
e
M
a
p
p
i
n
g
R
e
s
o
u
r
c
e
D
e
-
M
a
p
p
i
n
g
OFDM
OFDM
TX
RX
C
h
a
n
n
e
l
System Model
Figure 4.1: Generic OFDM system downlink diagram. Several users are multiplexed onto the
same OFDM carrier signal. The OFDM signal is transmitted via the channel to the receiver,
where only one user signal is extracted. The blocks inside the box are the focus of this chapter.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 20
4.2 Analytical model of OFDM System
In this section, an analytical time-domain model of an OFDM transmitter and receiver, as well
as a channel model, are derived.
4.2.1 Transmitter
The s
th
OFDM symbol is found using the s
th
subcarrier block, X
s
[k]. In practice, the OFDM
signal is generated using an inverse DFT. In the following model, the transmitter is assumed ideal,
i.e. sampling or ltering do not aect the signal on the transmitter side. Therefore, a continuous
transmitter output signal may be constructed directly using a Fourier series representation within
each OFDM symbol interval.
Each OFDM symbol contains N subcarriers, where N is an even number (frequently a power
of two). The OFDM symbol duration is T
u
seconds, which must be a whole number of periods
for each subcarrier. Dening the subcarrier spacing as , the shortest duration that meets this
requirement is written as:
T
u
=
2
=
2
T
u
= 2f (4.1)
Using this relation, the spectrum of the Fourier series for the duration of the s
th
OFDM symbol
is written as:
X
s
() =
N/21
k=N/2
X
s
[k]
c
( k) (4.2)
In order to provide the OFDM symbol in the time-domain, the spectrum in (4.2) is inverse
Fourier transformed and limited to a time interval of T
u
. The time-domain signal, x
s
(t), is
therefore written as:
x
s
(t) = F {X
s
()}
T
u
(t)
=
_
1
T
u
N/21
k=N/2
X
s
[k]e
jkt
0 t < T
u
0 otherwise
(4.3)
(4.4)
where
T
u
is a unity amplitude rectangular gate pulse of duration T
u
. Following the frequency-
to time-domain conversion, the signal is extended, and the cyclic prex is added:
x
s
(t) =
_
_
_
x
s
(t +T
u
T
g
) 0 t < T
g
x
s
(t T
g
) T
g
< t < T
s
0 otherwise
(4.5)
where T
g
is the cyclic prex duration and T
s
= T
u
+T
g
is the total OFDM symbol duration. It
should be noted, that (4.5) has the following property:
x
s
(t) = x
s
(t +T
u
) 0 t < T
g
(4.6)
that is, a periodicity property within the interval [0, T
g
]. The transmitted complex baseband
signal, s(t), is formed by concatenating all OFDM symbols in the time-domain:
s(t) =
S1
s=0
x
s
(t sT
s
) (4.7)
c
Aalborg University 2004 Technical Report: R-04-1002 Page 21
This signal is nally upconverted to a carrier frequency and transmitted:
s(t) = e
_
s(t)e
j2f
c
t
_
(4.8)
where s(t) denotes the transmitted RF signal and f
c
is the RF carrier frequency. For frequency
hopping systems, the carrier frequency is changed at certain intervals. This is written as:
f
c
[s] = f
c,0
+f
h
[s] (4.9)
where f
c
[s] is the carrier frequency for the s
th
OFDM symbol, f
c,0
is the center frequency of the
band and f
h
[s] is the frequency deviation from the band center when transmitting the s
th
OFDM
symbol. The period of f
h
[s] is , where is the hopping sequence period measured in whole
OFDM symbols.
The transmitter model described in this section is illustrated in Figure 4.2.
PSfrag replacements
X
s
N
2
X
s
[k]
X
s
N
2
1
e
j(
N
2
)t
e
jkt
e
j(
N
2
1)t
e
j2fc[s]t
CP+
x
s
(t) x
s
(t) s(t) s
c
(t)
IDFT
Figure 4.2: Transmitter diagram for the OFDM analytical model, given by (4.1)(4.9). The
subcarriers for the s
th
OFDM symbol each modulate a carrier, which are separated by . The
resulting waveforms are then summed, and the CP is added. The symbol represents the
concatenation of the OFDM symbols, given by (4.7). The resulting signal is then converted to a
carrier frequency and transmitted.
4.2.2 Channel
The channel is modeled as a time-domain complex-baseband transfer function, which may then
be convolved with the transmitted signal to determine the signal at the receiver side. The channel
baseband equivalent impulse response function for the u
th
user,
h
u
(t) is dened as:
h
u
(, t) =
L
l=0
h
u,l
(t)
c
(
l
) (4.10)
where h
u,l
(t) is the complex gain of the l
th
multipath component for the u
th
user at time t.
The channel is assumed to be static for the duration of one OFDM symbol, and the path gain
coecients for each path contribution are assumed to be uncorrelated. No assumption is made
c
Aalborg University 2004 Technical Report: R-04-1002 Page 22
PSfrag replacements
r
c
(t) s
c
(t)
c
(t)
h
u,s
(t)e
j2fc[s]t
sT
s
t < (s + 1)T
s
Figure 4.3: A diagram of the channel model given by (4.10) (4.11). The transmitted signal
passes through the channel, and noise is added.
for the autocorrelation properties of each path, except in the case of frequency hopping systems.
In such systems, the channel is assumed to be completely uncorrelated between two frequency
hops, provided that the distance in frequency is suciently large.
As the channel is assumed to be static over each OFDM symbol, (4.10) is redened as:
h
u,s
(t) =
L
l=0
h
u,l
[s]
c
(t
l
) (4.11)
where
h
u,l
[s] = h
u,l
(t); sT
s
t < (s + 1)T
s
The corresponding frequency-domain channel transfer function, H
u,s
, can then be found using
Fourier transformation:
H
u,s
() = F
_
h
u,s
(t)
_
=
_
h
u,s
(t)e
jt
dt (4.12)
The time-domain channel model is illustrated in Figure 4.3.
4.2.3 Receiver
The signal at the receiver side consists of multiple echoes of the transmitted signal, as well as
thermal (white gaussian) noise and interference. The RF signal received by the u
th
user is written
as:
r(t) = e
_
( s(t)
h
u,s
(t))e
j2f
c
[s]t
_
+(t); sT
s
t < (s + 1)T
s
(4.13)
where (t) is a real valued, passband signal combining additive noise and interference. The
receiver now has to recreate the transmitted signal. Aside from noise and multipath eects,
other imperfections in the receiver may also aect this process:
Timing error: In order to demodulate the signal, the receiver must establish the correct timing.
This means that the receiver must estimate which time instant corresponds to t = 0 in the
received signal (as seen from the transmitted signal point of view. As there are dierent
uncertainties involved, a timing error of t is assumed.
Frequency Error Similarly, the local oscillator of the receiver may oscillate at an angular
frequency that is dierent from the angular frequency of the incoming signal. This dierence
is denoted = 2f.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 23
The shifted time scale in the receiver is denoted t
= t t. Furthermore, due to the angular
frequency error , the down-converted signal spectrum is shifted in frequency. The down-
converted signal is therefore written as:
r(t) = ( s(t
h
u,s
(t))e
jt
+ (t
); sT
s
t < (s + 1)T
s
(4.14)
where (t) is the complex envelope of the down-converted AWGN. The signal is divided into
blocks of T
s
each, and the CP is removed from each of them. The s
th
received OFDM symbol
block, y
s
(t) is dened as:
y
s
(t) = r(t
sT
s
); 0 t < T
s
(4.15)
The signal block corresponding to x
s
(t), y
s
(t) is found by removing the CP from the each y
s
(t):
y
s
(t) = y
s
(t +T
g
); 0 t < T
s
T
g
(4.16)
which can be rewritten as:
y
s
(t) = y
s
(t +T
g
); 0 t T
u
= r(t
+T
g
sT
s
)
= ( s(t
+T
g
sT
s
)
h
u,s
(t))e
jt
+ (t
+T
g
sT
s
)
= ( x
s
(t
+T
g
)
h
u,s
(t))e
jt
+
s
(t
)
= ( x
s
(t
h
u,s
(t))e
jt
+
s
(t
) (4.17)
where
s
(t
) is the noise signal block of duration T
u
corresponding to the s
th
OFDM symbol.
In order to recreate the transmitted subcarriers, N correlators are used, each one correlating
the incoming signal with the k
th
subcarrier frequency over an OFDM symbol period:
Y
s
[k] =
1
T
u
_
T
u
0
y
s
(t
)e
jkt
dt (4.18)
In order to determine the correlator output, (4.18) may be seen as taking the continuous Fourier
transform of (4.17) multiplied by the rectangular pulse
T
u
(t) and evaluating it at the corre-
sponding subcarrier frequency. Assuming that the timing error is low enough to avoid ISI:
0 t < T
g
max(
l
)
the continuous Fourier transform can be written as:
Y
s
() = F { y
s
(t)
T
u
(t)}
= F
_
( x
s
(t
h
u,s
(t))e
jt
+
s
(t
)
_
T
u
e
j
sinc
_
_
= F
_
( x
s
(t
h
u,s
(t))e
jt
_
T
u
e
j
sinc
_
_
+N
s
()
= F
_
x
s
(t
h
u,s
(t)
_
c
( ) T
u
e
j
sinc
_
_
+N
s
()
= e
jt
F
_
x
s
(t)
h
u,s
(t)
_
c
( ) T
u
e
j
sinc
_
_
+N
s
()
= e
j(t+
)
N/21
=N/2
X
s
[k
]H
u,s
(k
)sinc
_
k
_
+N
s
() (4.19)
c
Aalborg University 2004 Technical Report: R-04-1002 Page 24
where
N
s
() = F
_
s
(t
)
_
T
u
e
j
sinc
_
_
(4.20)
is the Fourier transform of the AWGN contribution. The correlator output at the k
th
correlator
is then found as:
Y
s
[k] = Y
s
(k)
= e
jk(t+
)
N/21
=N/2
X
s
[k
]H
u,s
(k
)sinc
_
k k
_
+N
s
(k) (4.21)
For zero frequency error, (4.21) reduces to:
Y
s
[k] = e
jk(t+
)
X
s
[k]H
u,s
[k] +N
s
[k]; = 0 (4.22)
where
N
s
[k] = N
s
(k) (4.23)
H
u,s
[k] = H
u,s
(k) (4.24)
From (4.21), it is seen that the k
th
correlator output, Y
s
[k] corresponds to the transmitted
subcarrier, X
s
[k], with AWGN, ICI and a complex gain term (amplitude and phase shift) due
to imperfect timing and channel eects. The analytical model for the receiver is illustrated in
Figure 4.4.
When estimating the channel, the constant phase rotation term and the channel transfer
function would be estimated jointly (as the receiver cannot discern between the two). In the
following, the timing delay phase shift is omitted for clarity. Dening the equalization factor for
the k
th
subcarrier of the s
th
OFDM symbol and u
th
user as Z
u,s
[k], the subcarrier estimate is
written as:
X
s
[k] = Z
u,s
[k] Y
s
[k]
= Z
u,s
[k] H
u,s
[k] X
s
[k] +Z
u,s
[k] N
s
[k] (4.25)
Assuming a zero-forcing, frequency-domain equalizer (as well as perfect channel estimation
and zero frequency error), the corresponding equalizer gain is written as:
Z
u,s
[k] =
1
H
u,s
[k]
and (4.25) is rewritten as:
X
s
[k] = X
s
[k] +
N
s
[k]
H
u,s
[k]
(4.26)
It is observed, that although this is an unbiased estimator for X
s
[k], the signal-to-noise ratio
decreases drastically for subcarriers in deep fades.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 25
PSfrag replacements
Y
s
N
2
Y
s
[k]
Y
s
N
2
1
e
j(
N
2
)t
e
jkt
e
j(
N
2
1)t
e
j2fc[s]t
CP-
y
s
(t) y
s
(t)
r(t) r
c
(t)
Tu
0
Tu
0
Tu
0
sT
u
sT
u
sT
u
DFT
Figure 4.4: Receiver diagram for the OFDM analytical model, given by (4.13)(4.22). The
received signal (suering from multipath eects and AWGN) is converted down to baseband.
The symbol represents the division of the received signal into blocks, given by (4.15). The CP
is removed from each block, and the signal is then correlated with each subcarrier frequency, as
shown by (4.18).
4.2.4 Sampling
Although the receiver may be modeled in the continuous time-domain, an OFDM receiver uses
discrete signal processing to obtain the estimate of the transmitted subcarriers.
When the received signal is modeled as a Dirac impulse train, i.e. an ideally sampled signal,
(4.17) is instead written as:
y
s,d
(t) =
N1
n=0
y
s
[n]
c
(t nT) (4.27)
where:
T =
T
u
N
(4.28)
is the sample duration and:
y
s
[n] = y
s
(nT); n {0, 1, ..., N 1} (4.29)
is the discrete sequence corresponding to the sampled values of y
s
(t). When (4.27) is inserted
into (4.18), the correlation becomes the Discrete Fourier Transform of the received signal. It can
be shown, however, that (4.21)(4.26) are still valid in the discrete-time case.
4.3 Single OFDM Symbol Baseband Model in Matrix Notations
In this section, we explain the above analytical model in matrix model, so that it becomes easier
to implement in simulation programs, such as in MATLAB simulations, we have to model all the
components in the transmission chain in matrix format, thus the following model will be very
useful in that regard. The baseband model for a single OFDM symbol s is shown in Figure 4.5.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 26PSfrag replacements
z
s
r
s
v
F
H
d
s
d
s
Receiver
IDFT
DFT
CP ADD
CP REM
Channel
+
T
cp
T
+
cp
F
G
s
Figure 4.5: Single OFDM Symbol System Model
The single symbol received signal r
s
C
[N
g
+N+
g
1]
may be written as
r
s
= G
s
T
cp
F
H
d
s
+v (4.30)
with
T
cp
=
NN
g
..
N
g
..
_
_
1
.
.
.
1
1
.
.
.
1
.
.
.
1
_
_
denoting the [N
g
+N N] cyclic prex insertion matrix, where N
g
is the number of samples in
the guard period, and with
G
s
=
_
_
g
n
[0] 0 . . . . . . . . . . . .
g
n+1
[1] g
n+1
[0] 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
g
n+L1
[L 1] g
n+L1
[L 2] . . . g
n+L1
[0]
.
.
.
.
.
.
0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
g
n+N
g
+N1
[L 1] . . . . . . g
n+N
g
+N1
[0]
_
_
denoting the [N
g
+N N
g
+N] time-domain channel convolution matrix, where g
n
[l] represents
the gain of the l
th
sample delayed path in respect to the rst path at time n of the time-varying
channel impulse response, and where L is the span of samples from the rst to the last considered
path. The vector v C
[N
g
+N1]
represents complex valued circular symmetric white Gaussian
noise with variance N
0
, and the matrix F
H
C
[NN]
corresponds to the IDFT operation and is
the hermitian transposed of the DFT-matrix F C
[NN]
.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 27
The received vector z
s
C
[N1]
after the DFT-operation may be expressed as
z
s
= FT
+
cp
r
s
(4.31)
= FT
+
cp
G
s
T
cp
F
H
d
s
+FT
+
cp
v (4.32)
with
T
+
cp
=
_
_
1
.
.
.
1
_
_
..
N
g
. .
N
denoting the [N N
g
+N] cyclic prex removal matrix. Assuming that N
g
(L1), the linear
convolution of the transmitted sequence and the channel corresponds to a circular convolution.
Assuming a time-invariant channel in the discrete time interval [n; n+N
g
+N 1], the received
vector z after the DFT-operation may be expressed as
z
s
= H
s
d
s
+n, (4.33)
with H
s
C
[NN]
denoting the frequency domain diagonal channel matrix, where the [k, k]
th
element of H
s
corresponds to the complex-valued channel gain of the k
th
sub-carrier. The vector
n C
[N1]
represents complex valued circular symmetric white Gaussian noise with variance
N
0
. An estimate
d
s
of the transmitted data symbols d
s
may be calculated from z
s
using various
topologies as indicated in Figure 4.6.
PSfrag replacements
d
s
n z
s
d
s
Frequency Domain Channel
H
s
Receiver +
1
Figure 4.6: Simplied Single OFDM Symbol System Model
c
Aalborg University 2004 Technical Report: R-04-1002 Page 28
Chapter 5
Multi-Antenna OFDM Systems
Wireless transmission is impaired by fading and interference as we have discusses in Section 2.
The increasing requirement of data rate and quality of service for wireless communications calls
for new techniques to increase spectrum eciency and to improve link quality [20]. OFDM has
proved to be very eective in mitigating adverse multipath eects of a broadband wireless chan-
nel. The IEEE 802.11a WLAN standard species channel coding (
1
2
rate convolutional coding
with a constraint length of 7) and frequency interleaving to exploit the frequency diversity of
the wideband channel, but this is ecient only if the channel is suciently frequency-selective,
corresponding to long channel delay spreads. In a at fading situation (or in relatively lesser
frequency-selective fading situation), all or most subcarriers are attenuated simultaneously lead-
ing to long error bursts. In this case, frequency interleaving does not provide enough diversity to
signicantly improve the decoding performance [21]. So exploiting spatial diversity is necessary
for any OFDM system [22].
Multiple Input Multiple Output (MIMO) technique has proved its potential by increasing
the link capacity signicantly via spatial multiplexing [23] and improving the link capacity via
space-time coding [24]. Numerous research works are being published on MIMO enhanced OFDM
based wireless systems. It is obvious that MIMO technique will be eectively used with OFDM
based systems for providing mobile multimedia in future with reasonable data rate and quality
of service (in terms bit error rate, BER).
5.1 Antenna Diversity
Diversity is the technique to improve link performance and/or increase data throughput by
manipulating the statistical characteristics of the wireless link. There are dierent forms of
diversity that are traditionally exploited in communications systems, such as temporal diversity
in time-selective fading channels, spectral diversity in frequency-selective fading channels and
spatial diversity in cases where the channel is neither time-selective nor frequency selective (i.e.
when system constraints preclude the use of temporal or spectral forms of diversity, spatial
diversity can be used to provide substantial improvement in system performance). For example,
Interleaving makes use of temporal diversity; and spread spectrum communications and OFDM
exploits spectral diversity.
Spatial diversity involves using of multiple antennas in transmitter and/or receiver. In a
broad sense, the antenna diversity or spatial diversity can be classied in two categories: transmit
diversity and receive diversity. The use of multiple antennas at the receiver is termed as receive
c
Aalborg University 2004 Technical Report: R-04-1002 Page 29
S/P CP DFT
S/P CP
Output
r
1,1
r
M,1
g
1,1
Data
Detection
DFT
OFDM Demodulator
OFDM Demodulator
MR Combiner
r
k
S/P CP DFT
r
2,1
OFDM Demodulator
g
2,1
g
M,1
r
1,k
r
2,k
r
M,k
Figure 5.1: Multiple Antenna Receiver Diversity with MRC at subcarrier level
antenna diversity and the vice versa for transmitter.
5.1.1 Receiver Diversity
Receive diversity can be exploited fairly easily. In principle, multiple copies of transmitted signal
are received at spatially separated antennas and they are appropriately combined according to
specic signal processing (combining) techniques, such as Selection Combining (SC), Maximum
Ratio Combining (MRC) or Equal Gain Combining (EGC). MRC is more complex compared
to SC and EGC, but yields the highest Signal-to-Noise Ratio (SNR) [4]. As the number of
receive antennas increases, the eective channel is seen as an additive Gaussian channel and the
outage probability is driven to zero [25]. In case of OFDM reception, the selection combining
can be separated into two dierent techniques, namely antenna selection combining (ASC) and
subcarrier selection combining (SSC).
Here we discuss the MRC receiver diversity in an OFDM system. In MRC, the signals at
the output of the receivers are linearly combined so as to maximize the instantaneous SNR. This
is achieved by combining the co-phased signals, which requires that the CSI is known at the
receiver. The SNR of the combined signal is equal to the sum of the SNRs of all the branch
signals.
For an MRC-OFDM system as shown in Figure 5.1, the combining operations are performed
at subcarrier level after the DFT operation, thus we denote the process as Post-DFT MRC or
subcarrier combining receiver [26]. The received OFDM signals at dierent antenna branches are
rst transformed via M separate DFTs. Their outputs are assigned to N diversity combiners.
In the linear combiner, the received signal of the m
th
antenna and the k
th
data subcarrier r
m,k
is
multiplied by complex weight factors g
m,k
, such that the signal branches are co-phased (i.e., all
branches have zero phase). The magnitudes of these factors, having the squared sum of one, are
assigned based on the instantaneous subcarrier power (or SNR) of each received signal branch.
If the power is small in one particular branch, then a small gain factor will be assigned, and vice
versa. The resultant signal envelope after adding up the branches is
r
k
=
M
m=1
r
m,k
g
m,k
(5.1)
In EGC, equal values are selected for the magnitudes of g
m,k
.
In [27], a way to improve the radio link quality by introducing M number of receiver anten-
nas in HiperLAN/2 model is presented. Signals from both antennas labelled as A and B, are
c
Aalborg University 2004 Technical Report: R-04-1002 Page 30
demodulated and the values of the k data subcarriers in an OFDM symbol R
A,k
and R
B,k
are
introduced in the combiner block. The combiner, according to a diversity algorithm, will merge
the subcarrier values and the channel state information in order to form the signal R
k
, which will
pass through the channel equalizer and send to the inner receiver. The simulations in [27] show
that MRC and SSC show a high reliability in dispersive channels. In another note, increasing
the number of antennas also signicantly improves the system performance, of course with the
expense of higher hardware cost. It has been shown that the system performance drastically re-
duces under low correlation between transmission channels, and a good performance is obtained
under highly correlated channels.
5.1.2 Transmitter Diversity
Receive diversity can be impractical in a number of applications. In those cases, using multiple
antennas at transmitter, which is referred as transmit diversity, can be more attractive. Typical
WLAN applications fall under this category. Transmit diversity assures that user mobile devices
will become simple and cheaper [25].
S.M. Alamouti proposed a simple transmit diversity technique in [24] which was generalized
by Vahid Tarokh et.el. to form the class of Space-Time Block Codes (STBC) [28]. Based on [24],
[29] applied transmit diversity scheme to OFDM system with two transmit (Tx) antennas and one
receive (Rx) antenna. [30] simulated an OFDM system with the transmit diversity scheme that
[29] proposed. It was demonstrated that although this scheme has low complexity and is easy
to implement, it provides considerable improvements in performance without any bandwidth
expansion. Gains of between 9 to 14 dB were observed depending on the transmission mode
and channel scenario at a BER of 10
4
for the case where two antennas are used in both the
transmitter and receiver. We will discuss STBC in detail in Section 5.2.2.
One way of achieving transmit diversity is using a simple Delay Diversity (DD) scheme [31].
Using DD, the original signal is transmitted via the rst antenna and (a) linearly time-delayed
version(s) of original signal is (are) transmitted via one (or more) additional antenna elements.
The limiting factor for such a diversity system is that the introduced delay is always shorter than
the cyclic prex (CP) to make sure that Inter-Symbol Interference (ISI) is avoided.
To overcome this limiting problem, Cyclic Delay Diversity (CDD) has been proposed in
[32],[21],[22]. In this case, the signal is not truly delayed between respective antennas but cycli-
cally shifted and thus, there are no restrictions for the delay times. The receiver structure in the
DD and CDD schemes are similar to each other. All the signal processing needed is performed in
time domain, so the duplication of the DFT operation for each receiving antenna branch is not
a requirement any more, thus the receiver has lower computational cost compared to STBC and
conventional diversity schemes. Moreover, it is possible to apply CDD as a transmit diversity
technique without the knowledge of CSI at the transmitter side.
We will briey discuss CDD as a mean for transmitter diversity in an OFDM system. Ap-
plying CDD in the transmitter randomizes a relatively at channel, which is not unusual in
indoor WLAN systems, in an ecient way. When we shift the OFDM signal cyclically and add
them up in the receiver linearly, we actually insert some virtual echoes on the channel response.
This eect increases the channel frequency-selectivity, thus higher order frequency diversity can
be achieved, which is eectively exploited by a COFDM system [33]. On average, CDD does
not increase or decrease the total number of errors in the received signal of an uncoded OFDM
system, but it changes the error distribution in a benecial way, yielding an increased coding
gain.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 31
FEC QAM IDFT
Cyclic delay
t
2
t
M
CP
CP
CP
Ant 1
Ant 2
Ant M
Input data stream
Figure 5.2: OFDM Transmitter with CDD; Cyclic shifts introduced in the original signal are
xed.
The transmitter diversity technique is presented in Figure 5.2. To prepare cyclically shifted
transmission signal after the IDFT operation, a cyclic delay of
m
(for m = 2...M) is introduced
to the m
th
antenna. M transmit antennas are available. The resulting CDD signal for m
th
antenna branch is
x
m
[n] = x[(n
m
)modN] =
1
N
N1
k=0
W
k
m
N
d
k
W
kn
N
(5.2)
m
is unique for all antenna branches. For the purpose of simple and ecient implementation, it
is usually chosen to be an integer number of samples of the OFDM signal.
1
is taken to be zero,
which means that the original signal is transmitted via the rst antenna element. After inserting
the cyclic delays, the CP is inserted in the conventional manner and the signals are transmitted
via all the antennas simultaneously.
The optimum cyclic shift for transmitter CDD system has been analyzed in [34]. In that
case, the channel is randomized as much as possible to introduce diversity via CDD. The CSI
is not known at the transmitter, thus there is a possibility that the channel with CDD is worse
than one of the branch channels.
5.1.3 Cyclic Delay Diversity in OFDM Receiver
Traditional receiver diversity combining schemes are explained in Section 5.1.1. Using any of
these schemes in an OFDM system requires multiple DFT blocks in the receiver as seen in Figure
5.1. If the number of receiver antenna branches is M, then M DFT blocks are required. This is
clearly an expensive arrangement. Thus, CDD as explained in Section 5.1.2 can be introduced
at the receiver, where the diversity combining is performed prior to the DFT operation [33,
Section 8.3], as shown in Figure 5.3. We can see that the receiver only requires one DFT block,
regardless of the number of receive antenna branches. At the receiver, the antenna branch signals
can be used for estimating the channel responses for each individual receiver antenna in order
to optimize the diversity combining based on the instantaneous channel behavior. This allows
for an optimized diversity combining using cyclic delays,
i
and complex gain factors, g
i
, where
i = 1, 2, ..., M and M is the number of diversity branches.
We denote this combining technique in the OFDM receiver as Pre-DFT Maximum Average
(signal-to-noise) Ratio Combing (Pre-DFT MARC)[22]. For dual antenna system, where g
1
=
a
and g
2
=
1 a, 0 a 1, are the magnitudes of the gain factors and
2
= n is the delay of
c
Aalborg University 2004 Technical Report: R-04-1002 Page 32
CP
Cyclic
delay
t
2
t
M
CP
CP
Channel
estimation
g
1
g
M
MARC/EGC
g
2
Calculated combined
channel transfer function
FEC
Data
detection
DFT
Output
data stream
Figure 5.3: OFDM receiver with Pre-DFT Combining CDD. The instantaneous channel is es-
timated from the received signals to determine the optimum cyclic shifts (and gain factors, if
MARC combining is performed).
branch two (in samples), we can obtain an expression that is proportional to the average SNR
over all subcarriers in terms of a and n as [22]:
SNR(a, n) = ah
H
1
h
1
+ (1 a)h
H
2
h
2
+ 2
1 a|h
H
1
W
n
N
h
2
|,
(5.3)
where h
1
and h
2
are the channel transfer functions (CTF) of the 1
st
and 2
nd
diversity branches
respectively,
H
denotes the conjugate complex transpose of a vector, N is the number of subcar-
riers, and W
n
N
= diag([W
0
N
, W
n
N
, W
2n
N
, ..., W
(N1)n
N
]), W
N
= e
j2/N
, represents the cyclic delay.
A phase rotation of the branch two signal by = (h
H
1
W
n
N
h
2
) leads to the result given in
(5.3) [22]. The selection of a and n for maximizing the SNR (5.3) has been demonstrated in [22].
If we select equal values for the gain magnitudes (i.e. g
1
= g
2
=
0.5 for the dual antenna
case), the combining technique is named as Pre-DFT Equal Gain Combining (Pre-DFT EGC).
A performance comparison is presented in [22] in terms of BER with and without coding,
between MRC for receiver diversity and CDD for transmitter and receiver diversity in the con-
text of IEEE 802.11a and/or HiperLAN/2 WLAN systems. CDD yields good diversity gains
although the performance of Post-DFT MRC is not reached. On Ricean channels, the optimized
schemes(i.e. Pre-DFT MARC as described in this section) perform much better than CDD with
xed delays(i.e. pure CDD at the transmitter as described in Section 5.1.2), while the gain in
Rayleigh channels is surprisingly small.
5.2 MIMO Techniques
MIMO systems utilize space domain along with temporal and spectral domain to increase the
capacity and link quality of wireless communications. The use of multiple antennas at both
ends of a wireless link promises signicant improvements in terms of spectral eciency and
link reliability. There are two techniques available in MIMO modelling, the rst being Spatial
Multiplexing (SM) and the other Space-Time Coding (STC).
c
Aalborg University 2004 Technical Report: R-04-1002 Page 33
S/P
&
vector
encoder
OFDM
MOD-1 P/S
&
vector
decoder
(Estimates a
and decode)
a
1
a
M
Rich scattering
environment,
H
Received
data
OFDM
MOD-M
OFDM
DEMOD
and
signal
Separation
Figure 5.4: OFDM Based Spatial Multiplexing
5.2.1 Spatial Multiplexing Algorithms
Spatial multiplexing also known as the Bell-labs LAyered Space-Time (BLAST) system yields
substantial increase in data rate in wireless radio link. Two types of BLAST algorithms are avail-
able; one is called Vertical-BLAST (VBLAST) [35] and the other is Diagonal-BLAST (DBLAST)
[23]. V-BLAST as it is devised in [35] is presented in this section.
VBLAST increases data rate by transmitting independent information streams on dierent
antennas. No channel knowledge at the transmitter is required. The capacity improvement is
achieved by orthogonal channel matrix, H. In VBLAST, a single data stream is demultiplexed
into M substreams, and each substream is then encoded into symbols and fed into respective
transmitter. Tx-1 to Tx-M operate co-channel at symbol rate
1
T
symbols/sec. Each transmitter
is itself an ordinary QAM modulator. The receivers, Rx-1 to Rx-N, all operate in co-channel
also, each receiving the signals from all M transmit antennas. A quasi stationary view point
is taken into account, where the channel time variations are stationary for a burst period, and
channel is estimated correctly for each burst period.
Narrowband model of V-BLAST MIMO channel can be expressed as:
H =
_
_
_
_
_
h
1,1
h
1,2
. . . h
1,M
h
2,1
h
2,2
. . . h
2,M
.
.
.
.
.
.
.
.
.
.
.
.
h
N,1
h
N,2
. . . h
N,M
_
_
_
_
_
(5.4)
where the matrix transfer function of the channel is
H
[N,M]
, h
i,j
is the complex transfer function
from transmitter j to receiver i and M N.
The input-output relationship of [N, M] matrix channel is
r =
H s + n, (5.5)
where r =
_
r
1
r
2
. . . r
N
T
is a [N, 1] received signal vector, s =
_
s
1
s
2
. . . s
M
T
is
a [M, 1] transmit signal vector, and n =
_
n
1
n
2
. . . n
N
T
is a [N, 1] additive noise and
interference vector where all components are random complex numbers.
The essential dierence between D-BLAST and V-BLAST lies in the vector encoding process.
In DBLAST, redundancy between the substreams is introduced through the use of specialized
inter-substream block coding. The DBLAST code blocks are organized along diagonals in space-
time. In V-BLAST the vector encoding process is simply a demultiplex operation followed by
c
Aalborg University 2004 Technical Report: R-04-1002 Page 34
S
-S
1
2
*
S
S
2
1
*
Transmit
antenna 1
Transmit
antenna 2
Receive
antenna
+
Channel
estimator
Combiner
Maximum likelihood decoder
h
2
h
1
h
1
h
2
s
1
s
2
h
1
h
2
n
1
n
2
Additive noise
and interferences
Received data after detection
Figure 5.5: Alamoutis Space-Time Block Coding Scheme
independent bit-to-symbol mapping of each substream. No inter-substream coding, or coding
of any kind is required, though conventional coding of individual substreams may certainly be
applied [35].
Figure 5.4 presents an OFDM-based spatial multiplexing based on VBLAST algorithm. In
an OFDM-based spatial multiplexing system, transmission takes place simultaneously from all
M number of Tx antennas. The channel coded source data streams are rst serial-to-parallel
converted and vector encoded according to VBLAST algorithm. Later the respective symbol
blocks are passed through OFDM modulator (OFDM MOD in Figure 5.4) and then OFDM
symbol blocks are launched from the individual transmit antennas. In the receiver, the individual
signals are OFDM demodulated, separated and then vector decoded to recover the original source
data.
5.2.2 Space-Time Coding
[24] presented the transmitter diversity scheme for wireless communications which is a special
form of STC. There are two forms STC available, Space-Time Block Codes (STBC) and Space-
Time Trellis Codes (STTC). The original STC algorithm that [24] proposed is a two branch
transmit diversity with one receiver, in another word it is a form of STBC [28].
This section describes the Alamouti 2Tx-1Rx (2 transmitters - 1 receiver) STBC scheme. In
this scheme, two blocks of symbols namely s
1
and s
2
are transmitted at the same time from the
transmitter antennas. In the rst instance, s
1
and s
2
are transmitted from transmit antenna 1
(Tx1) and transmit antenna 2 (Tx2) respectively. In the following instance, s
2
and s
1
are sent
from the antennas respectively (s
1
means the complex conjugate of s
1
). The channel between the
Tx1 and receiver at time t,h
1
(t), can be modelled by a complex multiplicative distortion; similarly
the channel between Tx2 and receiver can be termed as h
2
(t). Assuming that the multipath
c
Aalborg University 2004 Technical Report: R-04-1002 Page 35
Space-
Time
Block
encoder
OFDM
MOD-1
STB
decoder
Received
data
OFDM
MOD-M
OFDM
DEMOD
Channel Estimator
Figure 5.6: Space-Time OFDM System with STBC Algorithm
fading is constant (or time-invariant) across two symbol blocks (i.e. quasi-static channel), it can
be written that
h
1
(t) = h
1
(t +T) = h
1
=
1
e
j
1
h
2
(t) = h
2
(t +T) = h
2
=
2
e
j
2
(5.6)
In the (5.6), T is the symbol duration. Denoting the received signals as r
1
and r
2
at time t
and t +T respectively; similarly additive noise and interference as n
1
and n
2
respectively where
n
1
and n
2
are complex random variables, the received signals can be expressed as
r
1
= r
1
(t) = h
1
s
1
+h
2
s
2
+n
1
r
2
= r
1
(t +T) = h
1
s
2
+h
2
s
1
+n
2
(5.7)
With the help of channel estimator, the combiner builds the following two combined signals
that are sent to the maximum likelihood (ML) detector:
s
1
= h
1
r
1
+h
2
r
2
=
_
2
1
+
2
2
_
s
1
+h
1
n
1
+h
1
n
2
s
2
= h
2
r
1
h
1
r
2
=
_
2
1
+
2
2
_
s
2
h
1
n
2
+h
2
n
1
(5.8)
These signals are then combined according to the ML principle as described in Figure 5.5
with the help of channel estimates.
It is observed that the diversity order in the 2Tx-1Rx STC is similar to that of 2-branch
Maximum Ratio Receiver Combining (MRRC). [24] also prescribed the way to design 2Tx-MRx
(2-branch transmit diversity with M receivers), to achieve a diversity order of 2M for the appli-
cations where a higher order of diversity is needed and multiple receive antennas at the remote
units are feasible. The total radiated power from Tx antennas is kept proportional to
1
M
; in
case of 2 Tx antenna, it is kept constant by transmitting half the power from each antenna. The
simulations show a 3-dB loss of performance of the scheme compared to MRRC; this is caused
by the fact that the transmitter does not know the channel, so no array gain is present in the
system [20].
The role of OFDM modem in the STC is similar to OFDM based BLAST system. The OFDM
modulation converts the frequency selective channel to frequency at channels, so that STBC
algorithm proposed can be applied to each at fading subchannel over two consecutive OFDM
symbols. High level block diagram of S-T OFDM system is shown in Figure 5.6. As in V-BLAST
OFDM systems in Figure 5.4, source data is S-T block coded and later OFDM modulated over
two consecutive OFDM symbols. These two symbols are sent to the receiver via the transmitter
antennas. In the receiver, the signals are jointly received and OFDM demodulated, before they
are separated and source data is recovered according to algorithm described in Figure 5.5.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 36
5.2.3 Space-Frequency Coding
Space-Frequency Coding (SFC) is actually implementation of Alamouti scheme [24] on OFDM
subcarrier basis. In this case, adjacent subcarriers are coded in a similar fashion as it is done
in STBC between two complete OFDM symbols. SFC is very interesting for severely frequency-
selective scenario. This topic will further be studied and included in the later versions of this
report.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 37
Chapter 6
Synchronization Issues
OFDM signal in time domain looks like a Gaussian noise because it is the superposition of many
subcarriers with random phases and amplitudes depending on user data. There are hundreds or
thousands of samples per OFDM symbol, since the number of samples necessary is proportional to
the number of subcarriers [13]. The subcarriers are spaced closer and closer together in frequency
domain when the number of subcarriers is increased to provide better data rate considering that
the available bandwidth is the same. This brings the need for stricter synchronization in the
system. Thus, synchronization is one of the most critical topics since OFDM demodulation is
virtually impossible with minute synchronization error.
There are three aspects of OFDM synchronization, namely subcarrier frequency synchroniza-
tion, receiver sampling frequency synchronization and symbol timing synchronization. The rst
one can be termed as frequency error and the last two can be grouped as timing error.
Subcarrier frequency oset error between the transmitter and the receiver can cause havoc in
OFDM reception. It can happen for two reasons, rst RF oscillator frequency mismatch between
the transmitter and the receiver and the channel Doppler shift. The frequency oset causes two
problems, one is the reduction of signal amplitude and the other is introduction of ICI [36]. The
carrier frequency oset must be less than 2% of inter-carrier distance [37]. This restriction is
obtained for normal Gaussian and typical Rician channels.
Symbol timing relates to the problem of detecting the start of a symbol. The requirement for
this is somewhat relaxed when CP is used to extend the symbol [13]. The symbol timing result
denes the DFT window; i.e. the set of samples used to calculate DFT of each received OFDM
symbol.
A quite dierent timing estimation problem is tracking the sampling clock frequency. The
oscillators used in DAC and ADC in transmitter and receiver respectively will never have exactly
the same period. Thus the sampling instants slowly shift relative to each other [25]. This will
result in incorrect sampling and thus increase the BER.
6.1 Symbol Timing Synchronization
Dierent OFDM systems have dierent requirements for symbol timing; for example, WLANs
cannot spend more time beyond the preambles whereas a broadcast system can spend several
symbols to acquire accurate symbol timing estimate. We will concentrate on WLAN case.
WLAN standards such as IEEE 802.11a and HiperLAN/2 species a preamble signal at the
beginning of the transmission. The preambles of 802.11a standard are presented in Figure 6.2
c
Aalborg University 2004 Technical Report: R-04-1002 Page 38
Synchronization Errors
Timing error Frequency error
Sampling
clock drift
Symbol
timing
RF oscillator
mismatch
Doppler
effect
Frequency
offset
Estimation
techniques
Timing
offset
Figure 6.1: Synchronization Error in any OFDM System
[38]. In both the standards, the preambles are designed such that the start of the symbols can
be easily determined at the beginning of the transmission. The rst 10 parts starting from A
1
to
A
10
are all short training symbols; all of them are 16 samples long. The lasttwo parts C
1
and C
2
are long training symbols that span 64 samples as it is for a regular OFDM symbol. The middle
part CP is 32 samples long and saves the long training symbols from multipath interferences.
The knowledge of the preamble is available to WLAN receiver, thus it can easily make use
of a simple cross-correlation technique for symbol timing. After the packet detection algorithm
signals the start of a packet, the symbol timing algorithm renes the estimation to sample level
precision. This is done by using the cross-correlation between the received signal r
n
and a known
reference t
k
; for example the end of the short training symbols or the start of the long training
symbols. The value of n that corresponds to the maximum absolute value of the cross-correlation
is the symbol timing estimate [25]. Mathematically it is shown in equation 6.1:
i
s
= arg max
n
_
_
L1
k=0
r
n+k
t
2
_
_
(6.1)
In a multipath environment the symbol timing estimation can be improved if an estimate
of the multipath taps h
n
of the channel impulse response is available [6]. In a multipath en-
vironment, the rst arrived path is not necessarily the strongest path. Thus cross-correlation
algorithm may take a high correlation value corresponding to paths that arrive later than rst
path. In that case, the signal energy at the rst path is lost. If the knowledge of h
n
is available,
then the timing point can be changed such that the energy of h
n
inside the DFT window can be
maximized.
The method that is mentioned above is non-data aided method, where only CP is used to
minimize the symbol timing error. There are data aided methods available also, which are used
in practical OFDM systems. In data-aided methods, pilots are inserted in various locations of
the signals, and symbol timing is derived based on the known pilots.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 39
A
1
A
2
A
3
A
4
A
5
A
6
A
7
A
8
A
9
A
10
CP C
1
C
2
10*0.8 s=8.0 s m m 1.6m m m s+2*3.2 s=8.0 s
8.0 s+8.0 s = 16.0 s m m m
Packet detection,
AGC, diversity scheme
Coarse frequency
offset estimation
symbol timing
Channel estimation
fine frequency offset estimation
Figure 6.2: OFDM Preamble Structure Specied in IEEE 802.11a Standard
6.2 Sampling Clock Synchronization
Considering a relative sampling clock oset between the transmitter and the receiver of
=
T
T
T
, (6.2)
where T and T
are the sampling times in transmitter and receiver respectively. With this, the
overall eect in the frequency domain (i.e. after the DFT block) on the k
th
received subcarriers
of i
th
OFDM symbol, R
i,k
, is [39]:
R
i,k
= exp
_
j2ki
T
sym
T
u
_
X
i
(k)sinc(k)H
i,k
+N
(i, k) (6.3)
Here, H
i,k
refers to channel channel frequency response of i
th
OFDM symbol in k
th
subcarrier
and N
(i, k) is the additional interference due to the sampling frequency oset. The power of
this term is approximated by
P
2
3
(k)
2
(6.4)
(6.4) shows that the degradation increases with the square of the amount of the oset and it
is the highest for outer most subcarriers [25].
Using pilot subcarriers for estimating the sampling frequency error is one of the techniques
that are mostly found in the literature. The sampling frequency oset is estimated by using the
knowledge of the linear relationship between the phase rotation caused by oset and the pilot
subcarrier index [25].
A method that is presented in [40] introduces two sets of pilot subcarriers; p
1
corresponds to
pilots on negative subcarriers and p
2
corresponds to pilots on positive subcarriers. The received
pilots can be represented by:
R
i,k
= H
k
p
i,k
exp
_
j2ki
T
sym
T
u
_
(6.5)
Now, if we calculate the rotation between two consecutive pilots, we nd that
i,k
= R
i,k
R
i1,k
= H
k
p
i,k
e
j2ki
T
sym
T
u
_
H
k
p
i1,k
e
j2k(i1)
T
sym
T
u
_
= H
k
p
i,k
e
j2ki
T
sym
T
u
H
k
p
i1,k
e
j2k(i1)
T
sym
T
u
= |H
k
|
2
|p
i,k
|
2
e
j2k
T
sym
T
u
(6.6)
c
Aalborg University 2004 Technical Report: R-04-1002 Page 40
The cumulative phases of
i,k
is calculated next for the sets of pilots p
1
and p
2
, which is
explained in (6.7):
1,i
=
_
_
kp
1
i,k
_
_
&
2,i
=
_
_
kp
2
i,k
_
_
(6.7)
Now the sampling frequency oset can be estimated from the equation above:
=
1
2
T
sym
T
u
1
min
kp
2
(k) + max
kp
2
(k)
(
2,i
1,i
) (6.8)
6.3 Carrier Frequency Synchronization
The Local Oscillators at the Transmitter and the Receiver may not be at the same frequency.
Since they are analogue high frequency components they cannot be at the same frequency. There
will almost always be some error say of the order of a few ppm be there. This is referred to as
carrier frequency oset. This error results in monotonically increasing or decreasing phase error
with time. The accumulated phase error will rotate of the symbol constellation in the receiver
causing the error in the decision during the demodulation of the symbol. This error goes on
accumulating with time. It is very dicult to correct the oscillator frequency, instead most of
the implementations allow the LO to run at its frequency but estimate the frequency oset and
apply compensation accordingly to nullify the phase accumulation. IEEE 802.11a allows the use
of short training sequence to perform the coarse frequency estimation [14]. Further there are
long training sequence in IEEE 802.11a for ne frequency synchronization.
Various algorithms that have been developed to compensate carrier frequency oset can be
classied under three dierent groups; namely Data Aided algorithms (DA) which are based
on special training symbols embedded in the transmission signal, Non-Data Aided algorithms
(NDA) that analyzes the signal in frequency domain and CP based algorithms that use the
inherent structure of the OFDM signal provided by the CP [41]. Out of these three, DA methods
are most suited for WLANs, as the WLAN standards specify preambles that contain training
symbols and can easily be used for the synchronization purpose.
There are principally two dierent approaches for this, one is time domain approach which is
performed in received signal before it goes through the DFT block and the other one is frequency
domain approach which is performed after the DFT operation. A very good description of these
two approaches is placed in [25]. Here we present the time domain approach in detail.
Let the transmitted signal be S
n
, then the complex base band model of the passband signal
y
n
is
y
n
= S
n
e
j2f
tx
nT
sym
(6.9)
where f
tx
is the transmitter carrier frequency. After down conversion at the receiver using carrier
frequency f
rx
the received complex baseband signal r
n
, ignoring the impairments due to noise
and channel is
r
n
= x
n
e
j2f
nT
sym
(6.10)
where
f
= f
tx
f
rx
(6.11)
c
Aalborg University 2004 Technical Report: R-04-1002 Page 41
The short training sequence is periodic after say . Then the estimation method for frequency
oset is
c =
1
l=0
r
l
r
l+
(6.12)
after simplication of (6.12) we get
c = e
j2f
T
sym
1
l=0
|x
l
|
2
(6.13)
Thus we get the estimate of the carrier frequency oset as
f
= 1/(2T
sym
)c. (6.14)
This is a common time domain estimation of coarse frequency oset. The long training
sequence of IEEE 802.11a is used for ne frequency estimation. The method followed is similar
except that the the value of changes.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 42
Chapter 7
Channel Estimation
Current OFDM based WLAN standards such as IEEE802.11a and HiperLAN2 use variations
of Quadrature Amplitude Modulation (QAM) schemes for symbol mapping which require a
coherent detection method in the receiver. And naturally, data detection in coherent OFDM
receivers require an accurate (or near accurate) estimate of Channel State Information (CSI). In
non-coherent methods, the detection is performed based on the dierential information available
between successive symbols.
There are two major kinds of channel estimators that are found in literature, namely pilot
assisted and blind estimation. A mixture of these two, where a blind method with limited training
symbols is used, is called semi-blind technique.
Traditional one-dimensional channel estimation techniques for the OFDM systems can be
summarized as follows: Least Squares (LS), Minimum Mean Squared Error (MMSE) and linear
MMSE (LMMSE). LS estimators are very simple to constitute, but they suer from MSE in low
SNR conditions. MMSE, based on time domain estimations, are high complexity estimators that
provide good performance in sampled-spaced channels, but limited performance in non-sample-
spaced channels and high SNR conditions. The third one, LMMSE provides good performance
in both sampled and non-sampled channels [42].
7.1 Exploiting Channel Correlation Properties for CSI Estima-
tion
In OFDM systems, the Doppler eects are kept smaller by making sure that the symbol duration
is much smaller compared to the channel coherence time. In this case, the channel attenuations at
successive symbol durations experience suciently higher time correlation. Similarly, if subcar-
rier spacing is chosen in a way that the spacing is much smaller than the coherence bandwidth
of the channel, the channel attenuations at the adjacent subcarriers will be highly frequency
correlated. So, the estimator can exploit both of these two correlation properties [43].
Figure 7.1 emphasizes the role of channel estimation in coherent detection of a WLAN OFDM
receiver. Channel estimation is performed after the FFT processing, and prior to data detection.
In this case, the estimated CSI is only used for equalization. Since each subcarrier is at fading,
all the techniques suitable for single carrier at fading systems are directly applicable to OFDM
subcarrier level.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 43
Analog
front
end
A/D
Frequency
correction
Offset
estimator
S/P
Frequency
offset
Time
offset
FFT
Cyclic prefix
dropped
Channel estimator
EQ P/S
Received
data
Figure 7.1: OFDM Receiver with Coherent Detection (using Channel Estimation)
Channel estimation of a SISO-OFDM
1
system can be done by using complete training symbols
after certain OFDM data symbols, or by inserting some training pilot tones in every OFDM
symbol. In the rst case, the CSI is estimated with the training symbol and interpolated for the
consecutive symbol before the next training symbol appears. This technique renders unacceptable
results when the channel variation time is comparable to OFDM symbol duration. The second
method is suitable in these kinds of fast varying channels. The CSI is estimated for all the
pilot tones using the pilot subcarriers from that particular symbol and later CSI for all other
subcarriers are obtained by interpolation. In that way, perfect or near perfect estimates are
achievable. But the cost is paid in signicant throughput reduction.
When channel is considered to be quasi-static, (i.e. the channel does not change much
between two consecutive OFDM symbols, in another words the channel coherence time is higher
than OFDM symbol duration), then the temporal correlation between two consecutive OFDM
data symbols can be used to improve the estimates. If the channel estimates for k
th
subcarrier
at l
th
time instance is denoted by
H(k, l) and
H(k, l +1) is the estimate for next time instance,
that is (l +1)
th
time instance for same k
th
subcarrier, then the best MSE estimator for
H(k, l +1)
given
H(k, l) and H(k, l + 1) is [44]
H(k, l + 1) = a
H(k, l) +bH(k, l + 1) (7.1a)
where a =
R
2
hh
(l) R
2
hh
(l + 1)
R
2
hh
(l) R
2
hh
(l + 1) +
2
R
2
hh
(l)
(7.1b)
and b =
2
R
2
hh
(l + 1)
R
2
hh
(l) R
2
hh
(l + 1) +
2
R
2
hh
(l + 1)
(7.1c)
In fact, using (7.1a), the temporal correlation properties are used for better channel estima-
tions. In a similar way, the channel frequency correlations can also be used between subcarriers
of an OFDM symbol.
7.2 Channel Estimation Based on Pilots
With an OFDM system, the wideband channel is sliced to a number of narrow band channels,
which are tagged to the respective subcarrier frequencies. Thus the trivial task of channel
equalization is reduced to simply estimating the channel transfer function, which are the narrow
bands. Such a channel can be estimated by inserting pilot symbols with known modulation
1
SISO refers to Single Input Single Output system, where the channel is modeled with one transmitter and one
receiver. SISO can be regarded as the counterpart of MIMO.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 44
f
|H(f)|
Figure 7.2: Channel Estimation with Pilot Symbols
scheme into the transmitted signal. Based on these pilot symbols, the receiver can measure the
channel transfer factors for each subcarrier using interpolation techniques [10].
Figure 7.2 illustrates pilot tone based channel estimation technique for OFDM systems. The
channel is estimated with the pilot symbols that are inserted (in dark color in the gure). The
attenuations of the pilot symbols are measured and the attenuations of the data symbols between
these pilot symbols are typically estimated/interpolated using time correlation property of fading
channel [43].
A simple mathematical description of optimum pilot-assisted channel estimation is presented in
[43]. In a matrix form, the observed symbols after the DFT operation in the receiver can be
written as
r =
X
h + n (7.2)
where the diagonal matrix
X contains the transmitted symbols on its diagonal (either known pilot
symbols receiver decisions of information symbols which are assumed to be correct), the channel
attenuations of one OFDM symbol (i.e. Fourier transform of h(t) evaluated at the frequency f
k
)
is collected in vector
h and the vector r contains the observed outputs of the DFT.
If we maximize the channel estimates in the Least-Square (LS) sense (minimizing
r
X
2
for all possible
h), then
h
ls
=
X
1
r =
_
r
0
X
0
r
1
X
1
. . .
r
N1
X
N1
_
T
(7.3)
This is a straight forward estimation technique where the received symbol on each subcarrier
is divided by the transmitted symbol to obtain the estimate. In the next step, the frequency
correlation can be used to smooth and improve the LS channel estimate.
The optimal Linear Minimum Mean-Square Error (LMMSE) estimate of
h (minimizing
E
_
2
_
for all possible linear estimators
h) becomes
h
lmmse
=
A
h
ls
(7.4)
where
A =
R
hhls
R
1
hlshls
=
R
hh
_
R
hh
+
2
n
_
X
X
H
_
1
_
1
and
R
hh
= E
_
hh
H
_
is the channel au-
tocorrelation matrix, that is the matrix that contains the correlations of the channel attenuations
c
Aalborg University 2004 Technical Report: R-04-1002 Page 45
Frequency
Time
S
t
S
f
Figure 7.3: An Example of Pilot Symbol Insertion Method
of the subcarriers. Similarly
R
hhls
denotes the correlation matrix between channel attenuations
and their LS-estimates, and
R
hlshls
denotes the autocorrelation matrix of the LS estimates.
The solution that is described above is computationally very extensive, because we need N
number of complex multiplications per estimated attenuation and also we need the knowledge
of SNR. Thus, practically LMMSE solution is not feasible to implement, but it is observed
that an optimal solution can be obtained starting from this solution. [45] has developed generic
complexity approximations of equation 7.4 whose performance can be made very close to LMMSE
solution.
7.2.1 Design of Pilot Based Channel Estimator
There are mainly two problems in designing channel estimators for wireless OFDM systems. The
rst problem concerns the choice of how pilots should be inserted. The second problem is the
design of the estimator as a low complexity with good channel tracking ability.
The pilot symbols should be inserted properly, so that it successfully estimates the frequency
response of the channel. The dierence between two consecutive pilot symbols in time and
frequency domain, S
t
and S
f
respectively, can be represented as
S
t
1
B
doppler
and S
f
1
max
(7.5)
Here B
doppler
is the Doppler spread. Figure 7.3 shows an example of such a pilot insertion
scheme [6].
Assuming that the pilot pattern is chosen, the optimal linear channel estimator in terms of
Mean-Square-Error (MSE) is a 2-D Weiner lter. Knowing statistical properties of the channel,
such a channel can be designed using standard techniques [16].
7.3 Channel Estimation Based on Training Symbols
Conventional estimation schemes send a stream of transmitted symbols with a modulation scheme
known to the receiver, and the receiver analyzes the eect of the channel on the known symbols
by observing the deviations on the received known symbols. These symbols are called Training
c
Aalborg University 2004 Technical Report: R-04-1002 Page 46
Symbols (TS). As this estimation technique solely depends on the TS, this type of channel
estimations are usually termed as TS-based channel estimation. The accuracy of the CSI is
dependent on the length of TS. It is worth mentioning here that the transmission of training
symbols reduces the spectral eciency of the system [6].
In WLAN systems, the training sequences as shown in Figure 6.2 are provided to facilitate
straightforward and reliable channel estimation. The long training sequence provided in the
WLAN IEEE 802.11a standard is to aid in obtaining the channel estimation. Since there are two
long training sequences, it can be averaged to improve the quality of the channel response. Since
the DFT is a linear operation, the average of the two sequences can be performed before DFT,
saving the computational resources. After the DFT processing, the received training symbols
R
1,k
and R
2,k
are a product of the training symbol L
k
and the channel Hk plus the additive
noise W
l,k
,
R
1,k
= H
k
L
k
+W
l,k
(7.6)
Since the long training sequence L
k
is known, we can compute the Channel Frequency response
as following:
H
k
=
1
2
(R
1,k
+R
2,k
) L
k
(7.7)
H
k
=
1
2
(H
k
L
k
+W
1,k
+H
k
L
k
+W
2,k
) L
k
(7.8)
H
k
= H
k
|L
k
|
2
+
1
2
(W
1,k
+W
2,k
) L
k
= H
k
+
1
2
(W
1,k
+W
2,k
) L
k
(7.9)
It is assumed here that the long training sequence has a magnitude of unity and the noise
samples W
l,k
and W
2,k
are statistically independent so there variance is half the variance of the
individual noise sample thus enhancing the SNR by 3 dB [14].
7.4 Blind Channel Estimation
Contrary to pilot based and training symbol based channel estimation techniques, blind channel
estimation requires no training symbol, instead certain known properties of the transmitted sym-
bols are observed to obtain a perfect or near perfect CSI. In this way, the spectral eciency in
increased, but the cost is paid in terms of increased computational cost. Furthermore, blind algo-
rithms does not converge very fast, thus limited amount of training symbols are used to converge
the computation faster, in which case the algorithms are termed as semi-blind algorithms.
There are some good numbers of blind algorithms thar are studied for OFDM systems. One
of the mostly used algorithm is well-known Constant Modulus AlgorithmCMA [46]. This topic
will further be studied in near future and some discussions will be added with future versions of
this report.
7.5 Channel Estimation in CDD-OFDM System
We have discussed CDD-OFDM system in Section 5.1.2 and Section 5.1.3. As shown in Figure
5.3, the channels are estimated immediately after the reception at the receiver front end in case
of Receiver CDD-OFDM system. In this section, we consider dual antenna receiver diversity
c
Aalborg University 2004 Technical Report: R-04-1002 Page 47
scheme with CDD. We denote the estimated value of CTFs h
1
and h
2
as
h
1
and
h
2
respectively.
The estimated combined channel frequency response as a function of n and g can be written as
h =
h
1
+
_
1 ge
j
W
n
N
h
2
, (7.10)
where the phase of the weight factors of 1
st
and 2
nd
branch signals are given by 0 and ,
respectively. g denotes the complex gain factors for combiner branches and n denotes the cyclic
delay (please refer to Section 5.1.3 for details).
With a 16-QAM or higher order constellations, it is necessary to know the CSI at the receiver,
i.e. the phase and gain of the CTF should be estimated correctly for correct data detection.
Because we are using narrow-band tones within multi-carrier system, we only need to estimate
a single value [47]. We assume that the channel is wide sense stationary in a sense that it is
constant in time for at least one complete OFDM symbol duration. Given a Minimum Mean
Square-Error(MMSE) channel estimator designed to cope with worst-case channel conditions,
the channel estimates for l
th
received OFDM symbol for i
th
diversity branch is well modelled as
the true CTF sample h
l,i
disturbed by AWGN n
H
l,i
[48]
h
l,i
= h
l,i
+n
H
l,i
, (7.11)
where the power
2
h
(
2
n
) of the estimation noise n
H
l,i
is a function of the channel noise variance. A
simple one-tap Recursive Least Squares(RLS) lter, which rst estimates the channel and then
normalizes the channel eect, can be used [49]. Mathematically,
h
i
k,l
=
r
i
k,l
s
k,l
+ (1 )
h
i
k,l1
(7.12a)
z
k,l
=
r
1
k,l
h
1
k,l1
+r
2
k,l
h
2
k,l1
|
h
1
k,l1
|
2
+|
1 g
h
2
k,l1
W
k
N
|
2
(7.12b)
s
k,l
= Quantize(z
k,l
), (7.12c)
where s
k,l
,
h
k,l
and z
k,l
are estimate of constellation points, estimate of demodulated channel and
decision variable (a noisy estimate of constellation value s
k,l
) for k
th
subcarrier and l
th
OFDM
symbol respectively, is the update factor in the estimate of the channel. s
k,l
is either a training
symbol or the quantized decision variable. Assuming no decision errors, the error in the estimate
of the subcarrier h
k,l
is then [47]:
2
n
H
l,i
=
2
N
S
2
E[
1
|x|
2
], (7.13)
where N
S
is the noise on the received signal.
7.6 Channel Estimation in MIMO Enhanced OFDM Systems
In MIMO-OFDM system, the number of channels that need to be estimated is [M, N], where M
represents the number of transmit antennas and N represents the number of receiver antennas.
Naturally the complexity with the estimation increases with increasing number of antennas at
any side of the channel. Practically all signals are transmitted simultaneously from the all M
transmit antennas, thus the received signal at any one of the N receivers is a superposition
c
Aalborg University 2004 Technical Report: R-04-1002 Page 48
of the transmitted signals of all the transmitter antennas at that instance of time. Thus, the
system should be modelled as follows: for the channel between i
th
transmit antenna and j
th
receive antenna, only the signal from i
th
transmit antenna is the desired signal and the rest are
interfering signals. To avoid this problem, some schemes suggest that the pilot tone that is used
by one antenna is not at all used by other antennas [50]. So interferences in pilot tones can
be avoided and correct CSI can be estimated. This method takes note that the time duration
between two consecutive OFDM symbols are higher than the channel coherence time, or no
channel temporal correlation information is available.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 49
Chapter 8
Research Challenges
Before discussing the research challenges, let us consider the user requirements and the bot-
tlenecks to realize such requirements. User requirements, such as higher link capacity, better
QoS and ubiquitous access (access to internet from anywhere and with any type of device), are
always present for discussion in any wireless system design process. There is also a requirement
of robust communication over wireless channel even at low data rates. The bottlenecks to these
requirements being primarily the channel itself, the stability, correctness and transient response
of radio frequency components, the xed word length of the hardware and limitation of battery
life for portable devices.
8.1 Wireless Channel Modelling
Wireless channel has always been a challenge to researchers and scientists. The hostility of wire-
less channel can never be eradicated, thus it is always the goal of system designers to overcome
the eects of channel on the received signal. In this respect, there are several parameters that
characterize a wireless multi-antenna communication system, such as antenna separation, propa-
gation terrain and/or foliage, Base Transceiver Station (BTS) antenna height, polarization, CCI,
range, wind speed /trac and mobile antenna height, etc, need to be studied and examined. Sev-
eral well-known channel models are found in the literature, but each addresses only some of the
parameters of wireless propagation, which are specic to the applications, to name a few, the
SISO models, the path loss model,average delay spread model, the K-factor model, the cluster
model approach, the UTRA model, the MIMO models, the ray tracing model, the METRA
model and the scattering model. There is denite need for a unied all encompassing channel
model that can be used in the development of MBWA. Such a model will be able to cover the
situation of xed wireless access (indoor oce model), low mobility situation (Pavement trac)
and high vehicular mobility.
8.2 Synchronization Issues
In Chapter 6, the details of the eect of synchronization issues have been dealt with. In WLAN
systems, the carrier frequency synchronization and symbol synchronization are done using the
preamble transmitted as the header of the packet. Some algorithms use the CP data for symbol
synchronization as well. In the case of broadcast systems a lot of pilot sub-carriers have to be
sent for synchronization purpose. So there is lot of forced wastage of spectrum.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 50
Also if there are some estimation errors in carrier frequency or symbol timing or sampling
clock, all the errors translate as rotation of the constellation points. So the success of OFDM
system depends strongly on synchronization. The higher the data rates are, the stricter the
synchronization requirements become. So in order to build systems to support higher and higher
data rates, there is a need for a range of algorithms and system design that facilitates robust
stimulation of the synchronization parameters with minimum computational complexity. Our
literature survey gave us the idea that the currently available algorithms are limited in their
performance in case of doppler shift and larger delay spread environment. Such systems with
one time estimate (non-real time estimate) of the synchronization parameters will not t the
mobile environment. New and ecient techniques are required to enable improved tracking of
environmental parameters that hinder the system.
Sampling clock synchronization is another parameter that eect the OFDM system. A drift in
the sampling clock manifests itself in the form of ICI. There are methods to estimate the sampling
clock drift for WLAN packet based systems, but these are either too complex to implement or
are not that robust in their performance. When the packet length is big, with very low SNR and
very high delay spread along with doppler shift, the accuracy and stability of these algorithms
comes to question. Another problem often encountered due to mismatch in sampling clock
frequencies is, the missing of a sample or over sampling of the incoming data. If this condition is
not traced and compensated, then the system performance will fall drastically in case of packet
based WLAN systems. A suitable system design to enable continuous tracking of sampling clock
can amazingly improve the overall error rate of the system.
8.3 Channel Estimation Issues
We have discussed some issues related to channel estimation in Chapter 7. Channel estimation
is a primary requirement of any receiver that perform coherent reception. The capacity of a
system is largely depended on the channel estimation scheme used in the system. The more
accurate the channel estimate is, the better the quality of service. OFDM oers a very simple
frequency domain channel estimation Scheme. Even though the scheme is simple enough it does
not perform accurately under very low SNR conditions. There are dierent techniques in Single
Carrier systems, such as Linear Equalizer (LE), Zero Forcing Equalizer (ZFE), Decision Feedback
Equalizer (ZFE) etc, but these are all time domain equalizers. Ecient yet robust techniques
can be thought of that use both frequency domain and time domain processing. There could be
possibilities of implementing Dynamic Cyclic Prex Length in order to dynamically increase the
data rate. The wireless channel though is a fading one, yet there is some coherence bandwidth and
the fading characteristics are not necessarily random, this fact can be exploited for implementing
better systems. One may optimize the performance by dynamic pilot allocation as well. There
can be optimization of TDD systems where the down link and up link data path can share the
channel information and thus can improve the throughput by pre-equalization.
The case of mobile environment throws up quite a few alternatives. Obviously, the channel
transfer function changes during the packet interval. Thus the estimation of the channel by
preamble may not be valid even after every symbol. A constant tracking mechanism is needed.
The DVB-T system uses many pilots in the symbol for this purpose, so a mix of pilot based
tracking plus preamble based initial estimate can be thought of as an alternative.
MIMO systems are being thought upon for implementation in MBWA IEEE 802.20. With
MIMO systems, new ways should be found for channel estimations. MIMO systems bring with
c
Aalborg University 2004 Technical Report: R-04-1002 Page 51
them the additional overload of multiple channel estimations, so it will be required that the
computation cost of such channel estimations need to be reduced. To conclude, the focus of the
channel estimation techniques should be low complexity and power ecient solutions.
8.4 Capacity Enhancement via MIMO
MIMO algorithms are usually derived from a narrow-band point of view. As the wideband
OFDM modulation converts the subcarriers to a narrowband channel, it should be possible to
implement all kinds of MIMO algorithms on subcarrier by subcarrier basis. MIMO channel
modelling promises an increase in data throughput of overall transmission channel, so using
OFDM with an amalgamation of MIMO concepts will denitely play a signicant role in future
WLAN systems. MIMO techniques should be studied more extensively to nd ecient ways for
increasing the data rate of the current OFDM systems. For example, SM opens multiple data
pipes between transmitter and receiver. Now when we increase the number of transmitter and
receiver antennas, we eectively increase the possibility of reaching higher data rate. But this
comes with some side eects, with increasing potentials for super data rate, the processing loads
also get increased which is not a pleasant situation. So, it is required that techniques should be
found to introduce MIMO advantages in an OFDM system in more ecient and reasonable way.
STFC techniques for MIMO systems is another important issue that can be looked into.
8.5 System Implementation
The role of OFDM as the possible physical layer contender for high data rate future wireless
communications is somewhat established by WLANs adoption of it as their PHY standard.
Understanding the demand for OFDM based system, there is a need to design OFDM based
systems for future wireless applications. OFDM involves complex system operations, which must
coincide with numerous constrains, such as timing, synchronization, RF impairments etc. Thus,
OFDM deserves a thorough study for better and more ecient designs. Numerous theoretical
researches are done on WLANs. Nevertheless, hardware implementations have not yet achieved
the maximum limit of the transmission data rate specied by the standards. So, developing
OFDM hardware for future systems is an immense need.
On the other hand, tremendous growth of recongurable hardware in recent years has made it
possible to implement complex telecommunications related digital signal processing algorithms.
There are several of FPGAs
1
available now with multimillion gates featured on them. FPGAs
have grown in their logic densities and have shrunk in the logic area tremendously. Recent FPGAs
are made of millions of logic gates with special multipliers banks, where highly computational
signal processing, such as OFDM, can be implemented. The recent FPGAs are complete and
concise in supporting OFDM operation. Moreover there are user-friendly tools available that can
be used to program the FPGAs in very short time. So, it is an immense requirement to design an
OFDM based Multicarrier Modulation (MCM) testbed in FPGA, where several dierent systems
can be tested in real life scenario.
Huge eorts are required on designing power ecient implementation of such systems, since
most of the systems require large amount of computations. May be a more power ecient system
with moderate data rate is the need of the day than a system that consumes a lot of energy to
1
Field Programmable Gate Arrays
c
Aalborg University 2004 Technical Report: R-04-1002 Page 52
give very high data rates. The eld is totaly open and one may go in any direction just carrying
only one objective to develop better but usable communication system.
8.6 Peak to Average Power Reduction
The peak to average power issue of OFDM systems was discussed in Section 3.5.2. Lot of eort
have been made to reduce the PAPR of OFDM systems. Let us rst discuss the steps that have
already been taken and the performance achieved by them so that we can nd out the area or
the path that may be tried out for further improving the situation.
There are a range of parameters, all trying to quantify the variation of the amplitude of
the OFDM symbol. Finally the factor that was accepted and used in most of the papers is
PF
2
=
max(Power)
rmsPower
[51]. Mostly non-linear amplitude clipping algorithm was used to reduce the
PAPR of OFDM systems. Amplitude clipping resulted in out-of-Band spectrum spillage. Also
the BER and PER performance was degraded by the implementation of the amplitude clipping
algorithms [6]. There are several clipping techniques discussed in [6] where each of the techniques
tries to minimize the out-of-band radiation, the BER and PER.
An alternative direction is to use coding of the incoming bit-stream such that the resulting
IFFT output had a lower PAPR [6, 51]. Shapiro-Rudin sequences were the early ones. These
codes assumed that the bit stream had to be BPSK modulated, i.e. the trigonometric series
would have coecients of either +/-1 only. Thus multilevel coding situation was not considered,
even though it achieved great performance for BPSK. It established an upper and lower bound
for the PAPR of coded OFDM. It was later shown that Shpairo-Rudin codes were a special case
of Golay complementary codes. For 16 carrier systems theoretical PAPR is about 12 dB , but
by using Shapiro-Rudin codes it can be brought down to 2.8 dB. Shephard [52] proposed the use
of Shapiro-Rudin codes for
1
2
-rate QPSK-OFDM. Golay codes were also proposed. Gloay codes,
found in 1961 are a set of complementary codes. Popovic showed that Golay codes provide the
benet that the PAPR is bounded by 2 (or 3) dB . Popovic also showed that Shapiro-Rudin codes
were a special case of Golay codes. It has been found that with Golay codes coding rate falls
much lower than
1
2
, when number of carriers exceed 16. So it cannot be eciently implemented
in case of high number of sub-carriers. Another class of codes called M-sequence (Maximum
Length) codes and partial M-sequence codes. Selected mapping was another technique that was
tried. Selected mapping technique had low overhead , but it was computationally intensive since
one had to nd the best mapping out of the set of randomly mapped codes.
All these codes mentioned above are designed for BPSK modulation systems. Not much
literature is found on techniques to reduce the PAPR for QPSK, QAM-16, QAM-64 and higher
order modulated OFDM systems with very large number of sub-carriers. So with the insight of the
already tried and proven methods for BPSK we can investigate and deisgn new coding shcemes
that may have the capability of reducing the PAPR for high data rate OFDM systems with
higher order modulation and very large number of sub-carriers. Combined codes can be designed
so that the Error Correcting Codes and PAPR reducing codes may not be seen separately, so as
to optimize the transmission/encoding and reception/decoding procedure.
8.7 Dynamic CP Length
The current standards are too robust with the channel impairments. The channel is strictly
taken as stationary indoor channel. By using the term stationary it is meant that between few
c
Aalborg University 2004 Technical Report: R-04-1002 Page 53
OFDM symbols, the channel is expected to become static, or not changing. Thus, it may be wise
to measure the channel maximum delays and insert the CP according to the measurement. In
that case, a technique has to be found to measure the maximum channel delays. This can be
done using the pilots that are inserted for channel estimation and synchronization process.
CP plays an important role in combating multipath eects by reducing ICI to maintain
orthogonality between subcarriers and eliminating the ISI. It is also the fact that inserting CP
has its own cost, a part of signal energy is lost since CP carries no information. The loss is
measured as [6]
SNR
loss
C
P
= 10log
10
_
1
T
CP
T
symbol
_
(8.1)
According to IEEE 802.11a standard, CP length is 0.8s and data part of OFDM symbol is
3.2s, thus complete OFDM symbol duration is 4.0s, which is 5 times the CP length. Using
the above equation, we can see that 0.97dB in SNR is lost to accommodate such amount of CP.
The standard species 0.8s as the CP duration considering the fact that the maximum RMS
delay spread at worse case condition can be up to 200ns, and the CP is taken as 4 times that
value. But in practice, the usual delay spread values in static indoor channels are 40 70ns [53].
Thus it is clear that to cater the worst case scenario, actually a large part of signal energy is
always being wasted.
Now we recount the loss of SNR due to CP insertion considering that we have a mechanism
in place that can measure the RMS delay spread dynamically. For example, we assume that
in average the maximum delay spread is somewhere in between 50ns to 100ns, then if we take
200ns as the CP length, then T
CP
= 0.2s and T
symbol
= 3.4s. With these new values,
SNR
loss
C
P
= 10log
10
_
1
0.2
3.4
_
= 0.26dB , so in this case by reducing the symbol length with
smaller CP length, (0.97 0.26)dB = 0.71dB of SNR can be saved.
In another way, if we maintain the OFDM symbol length so that T
CP
= 0.2s and T
symbol
=
4.0s, then we should be able to enhance the user data rate. New maximum data rate using best
case modulation (64-QAM) and channel coding according to the standard will be
_
1 +
0.80.2
4.0
_
54Mbps = 62.1Mbps. Of course, this will mean that the sub-carrier spacing will be little bit
smaller than the one specied in the standard, but this should cause any problem in the system
performance. This is a signicant improvement indeed. A suitable algorithm to perform this task
can be found by making use of the intelligent channel estimation algorithm that is envisioned in
Chapter 7. In this way, SNR gain or capacity enhancement can be assured without increasing
any processing.
8.8 OFDM Based Multi-User Systems
OFDM is now being stuied for multi-user systems, such as cellular wide area networks. Basically,
orthogonal frequency resources (i.e. orthogonal subcarriers) can be shared among users, which
is the simplest multiple access technique based on OFDM modulation. Besides, there are a
number of hybrid multiple access techniques that can be found in literature. Here hybrid means
an amalgamation of OFDM and multiple access techniques (with the main accent to the spread
spectrum) to provide an ecient multi-user scenario with very high data rate. The following is
a list of some of the most known multiple access techniques that can be found in the literature:
1. OFDMA (Orthogonal Frequency Division Multiple Access)
2. OFDMA-FSCH (OFDMA Fast SubCarrier Hopping, downlink of Flash-OFDM)
c
Aalborg University 2004 Technical Report: R-04-1002 Page 54
3. OFDMA-SSCH (OFDMA Slow SubCarrier Hopping, uplink of Flash-OFDM)
4. MC-CDMA (Multi-Carrier CDMA) [54]
5. OFDM-CDMA-SFH (OFDM-CDMA Slow Frequency Hopping) [55]
6. VSF-OFCDMA (Variable Spreading Factor - Orthogonal Frequency and Code Division
Multiple Access)
A comprehensive analysis of these access techniques can be found in [19]. At this moment,
tremendous research eorts are being spent on these techniques all over the world. It is undoubt-
edly a very important issue that still requires a lot more attentions and eorts.
8.9 Miscellaneous Research Directions
1. Other than the basic OFDM system for improvement, researchers in the eld of OFDM
have been working on improved channel coding techniques which can be designed for special
use with OFDM. New coding schemes are being thought of which shall be integrated with
OFDM. A lot of research is being done on turbo-coded OFDM for uplink and LDPC coded
OFDM for downlink.
2. Work is also in progress in using Walsh-Hadamard-OFDM or even DCT-OFDM system.
An additional transformation is being tried out to achieve improved performance in these
systems. Additionally a new line of thought is coming up towards pseudo orthogonal sub-
carrier spacing.
3. Smart antennas could still be thought of for OFDM systems since MIMO systems increases
the computational complexities several times. Smart antennas can be used for interference
mitigation and range extension of a cellular system. It can be very good solution, consid-
ering that MIMO complexities may be prohibitive to implement in the MS receiver.
4. Hybrid systems could be the next wave of communication technology after OFDM. A lot
of interest is gathering around MC-CDMA, UWB-OFDM and a mix of frequency hopping,
CDMA and OFDM.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 55
Chapter 9
Conclusion
This report intended to give a rst hand guide to understand the basics of OFDM. We specially
emphasized on PHY layer AI design related issues. Our main goal was to present the ins and
outs of any OFDM system, so we concentrated on several important issues like synchronization
and channel estimations etc. One of the primary aims was to identify possible future scopes
for research in OFDM system design. So considerable amount of eorts was spent on studying
existing wireless standards based on OFDM. We strongly believe that with the success OFDM
PHY standards such as IEEE 802.11a, OFDM will continue to play a great role in all future
generations of wireless systems. As we see it, MBWA systems will be one of the most dominating
wireless systems in future and OFDM will be the core technology for MBWA systems, we will
be concentrating our future eorts in designing a robust and power ecient MBWA systems for
future applications.
As we have mentioned in the preface, this report is written at the very beginning of our PhD
studies. As we proceed along with our studies, and we grow with knowledge and competencies
in OFDM, this report will be constantly updated and improved.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 56
Bibliography
[1] R. Prasad & L. Gavrilovska, Research Challenges for Wireless Personal Area Networks,
in Proc. of 3
rd
International Conference on Information, Communications and Signal Pro-
cessing (ICICS), Singapore, October 2001.
[2] Web ProForum, OFDM for Mobile Data Communications, Online Tutorial, Internet ad-
dress: http://www.ice.org/, 2000.
[3] M. Speth, OFDM Receivers for Broadband-Transmission, Internet article:
http : //www.ert.rwth aachen.de/Projekte/Theo/OFDM/www ofdm.html, 2001.
[4] J.G. Proakis, Digital Communications, 3rd ed. McGraw-Hill, New York, 1998.
[5] Y. Zhao, Principle of OFDM Systems, Lecture notes for S-72.137 Course, Communications
Laboratory, Helsinki University of Technology, Finland, Spring 2000.
[6] R.V. Nee & R. Prasad, OFDM for Wireless Multimedia Communications. Artech House
Publishers, 2000.
[7] W.Y. Zou & Y. Wu, COFDM: An Overview, IEEE Trans. Broadcasting, vol. 41, no. 1,
March 1995.
[8] E.P. Lawrey, Adaptive Techniques for Multiuser OFDM, Ph.D. dissertation, James Cook
University, Australia, December 2001.
[9] C.R. Nassar et al., Multi-carrier Technologies for Wireless Communication. Kluwer Aca-
demic Publishers, 2002.
[10] H. Rohling et al., Broad-band OFDM Radio Transmission for Multimedia Applications,
in Proc. of the IEEE, vol. 87, no. 10, October 1999, pp. 1778 1789.
[11] J.H. Scott, The How and Why of COFDM, BBC Research and Development, EBU
Technical Review, Winter 1999.
[12] J. Geier, Wireless LANs, Implementing High Performance IEEE 802.11 Networks, 2nd ed.
Sams Publishing, July 2001.
[13] D. Matic, OFDM Synchronization and Wideband Power Measurements at 60 GHz for Fu-
ture Wireless Broadband Multimedia Communications, Ph.D. dissertation, Aalborg Uni-
versity, Denmark, September 2001.
[14] U.S. Jha, Low Complexity Resource Ecient OFDM Based Transceiver Design, Ph.D.
dissertation, Aalborg University, Denmark, September 2002.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 57
[15] H. Sari et al., Transmission Techniques for Digital Terrestrial TV Broadcasting, IEEE
Comm. Mag., vol. 33, no. 2, pp. 100109, February 1995.
[16] Ove Edfors et al., An Introduction to Orthogonal Frequency-Division Multiplexing, Divi-
sion of Signal Processing, Lulea University of Technlogy, Sweden, Research Report 1996:16,
September 1996.
[17] T. Pollet et al., BER Sensitivity of OFDM Systems to Carrier Frequency Oset and Wiener
Phase Noise, IEEE Trans. Comm., vol. 43, no. 2-3-4, pp. 191193, February-April 1995.
[18] H. Rohling & T. May, Comparison of PSK and DPSK Modulation in a Coded OFDM
System, in Proc. IEEE VTC, Phoenix, Arizona, USA, 1997, pp. 57.
[19] M. I. Rahman et al., Comparison of Various Modulation and Access Schemes under Ideal
Channel Conditions, Aalborg University, Denmark, JADE project Deliverable, D3.1[1],
July 2004.
[20] H. Bolcskei & A.J. Paulraj, Multiple-Input Multiple-Output (MIMO) Wireless Systems.
CRC Press, 2002, ch. in The Communications Handbook, pp. 90.190.14.
[21] K. Witrisal et al., Antenna Diversity for OFDM using Cyclic Delays, in Proc. IEEE
8th Symposium on Communications and Vehicular Technology in the Benelux, SCVT-2001,
October 2001.
[22] M.I. Rahman et al., Performance Comparison between MRC Receiver Diversity and Cyclic
Delay diversity in OFDM WLAN Systems, in Proc. 6
th
WPMC, vol. 2, October 2003, pp.
198202.
[23] G.J. Foschini, Layered Space-Time Architecture for Wireless Communication in a Fading
Environment When Using Multiple Antennas, Bell Labs Technical Journal, pp. 4159,
Autumn 1996.
[24] S.M. Alamouti, A Simple Transmit Diversity Technique for Wireless Communications,
IEEE JSAC, vol. 16, no. 8, October 1998.
[25] J. Heiskala & J. Terry, OFDM Wireless LANs: A Theoritical and Practical Guide, 2nd ed.
Sams Publishing, July 2001.
[26] M. Okada & S. Komaki, Pre-DFT Combining Space Diversity Assisted COFDM, IEEE
Trans. Veh. Tech., vol. 50, no. 2, March 2001.
[27] J.D. Moreira et al., Diversity Techniques for OFDM Based WLAN Systems, in Proc.
IEEE PIMRC, Lisbon, Portugal, September 2002.
[28] V. Tarokh et al., Space-Time Block Coding for Wireless Communications: Performance
Results, IEEE JSAC, vol. 17, no. 3, March 1999.
[29] K.F. Lee & D.B. Williams, A Space-Time Coded Transmitter Diversity Technique for
Frequency Selective fading Channels, in Proc. IEEE Sensor Array and Multichannel Signal
Processing Workshop, Cambridge, Massachusetts, USA, March 2000, pp. 149152.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 58
[30] A. Doufexi et al., Design Considerations and Initial Physical Layer Performance results
for a Space Time Coded OFDM 4G Cellular Network, in Proc. IEEE PIMRC, Lisbon,
Portugal, September 2002.
[31] Y. Li et al., Transmitter Diversity for OFDM Systems and Its Impact on High-Rate Data
Wireless Networks, IEEE JSAC, vol. 17, no. 7, July 1999.
[32] A. Dammann & S. Kaiser, Performance of Low Complex Antenna Diversity Techniques
for Mobile OFDM Systems, in proc. 3
rd
International Workshop on Multi-Carrier Spread-
Spectrum, Oberpfaenhofen, Germany, September 2001.
[33] K. Witrisal, OFDM Air-Interface Design for Multimedia Communications, Ph.D. disser-
tation, Delft University of Technology, the Netherlands, April 2002.
[34] M. Bossert et al., On Cyclic Delay Diversity in OFDM Based Transmission Schemes, in
proc. 7
th
International OFDM Workshop, Hamburg, Germany, September 2002.
[35] P.W. Wolniansky et al., V-BLAST: An Architecture for Realizing Very High Data Rates
Over the Rich-Scattering Wireless Channel, in Proc. IEEE-URSI International Symposium
on Signals, Systems and Electronics, Pisa, Italy, May 1998.
[36] P.H. Moose, A Technique for Orthogonal Frequency Division Multiplexing Frequency Oset
Correction, IEEE Trans. Comm., vol. 42, no. 10, October 1994.
[37] L. Wei & C. Schlegel, Synchronization Requirements for Mmulti-user OFDM on Satellite
Mobile and Two-path Rayleigh Fading Channels, IEEE Trans. Comm., vol. 43, no. 2,
February 1995.
[38] LAN/MAN Standards Committee of the IEEE Computer Society, Part 11: Wireless LAN
Medium Access Control (MAC) and Physical Layer (PHY) Specications-High speed Phys-
ical Layer in the 5 GHz Band, ANSI/IEEE Std 802.11, 1999.
[39] M. Speth et al., Minimum Overhead Synchronization for OFDM Based Broadband Trans-
mission, in proc. IEEE GLOBECOM, vol. 5, 1998, pp. 2777 2782.
[40] S.A. Fechtel, OFDM Carrier and Sampling Frequency Synchronization and its Performance
on Stationary and Mobile Channels, IEEE Trans.on Consumer Elec., vol. 46, no. 3, Aug
2000.
[41] M.H. Hsieh & C.H. Wei, A Low-Complexity Frame Synchronization and Frequency Oset
Compensation Scheme for OFDM Systems Over Fading Channels, IEEE Trans. Veh. Tech.,
vol. 48, no. 5, September 1999.
[42] I. Tolochko & M. Faulkner, Real Time LMMSE Channel Estimation for Wireless OFDM
Systems with Transmitter Diversity, in proc. IEEE 56
th
VTC, vol. 3, Fall 2002, pp. 1555
1559.
[43] J. Beek, Synchronization and Channel Estimation in OFDM Systems, Ph.D. dissertation,
Lulea University of Technology, Sweden, September 1998.
[44] V.K. Jones & G.C. Raleigh, Channel Estimation for Wireless OFDM Systems, in Proc.
of IEEE GLOBECOM, 1998, pp. 980985.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 59
[45] Y. Li et al., Robust Channel Estimation for OFDM Systems with Rapid Dispersive Fading
Channels, IEEE Trans. Comm., vol. 46, no. 7, July 1998.
[46] D. Godard, Self-recovering Equalization and Carrier Tracking in Two-Dimensional Data
Communications Systems, IEEE Trans. Comm., vol. 28, pp. 18671875, Nov 1980.
[47] S.K. Wilson et al., 16-QAM Modulation with Orthogonal Frequency Division Multiplexing
in a Rayleigh-Fading Environment, in proc. IEEE 44
th
VTC, June 1994, pp. 16601664.
[48] M. Speth et al., Optimum Receiver Design for Wireless Broad-Band Systems Using OFDM
- Part I, IEEE Trans. Comm., vol. 47, no. 11, November 1999.
[49] R. Price, Error probabilities for Adaptive Multichannel Reception of Binary Signal, IRE
Trans. Info. Theory, vol. 8, pp. 305316, September 1962.
[50] Y. Li et al., MIMO-OFDM for Wireless Communications: Signal Detection with Enhanced
Channel Estimation, IEEE Trans. Comm., vol. 50, no. 2, pp. 14711477, September 2002.
[51] L.Hanzo et al., OFDM and MC-CDMA for broadband multi-user communications, WLANs
and Broadcasting. IEEE Press & Wiley, 2003.
[52] S. Shephard et al., Sipmple Coding Scheme to Reduce Peak Factor in QPSK Multicarrier
Modulation, IEEE Elec. Letters, vol. 31, pp. 11311132, July 1995.
[53] Matthew S. Gast, 802.11 Wireless Networks: The Denitive Guide, 1st ed. OREILLY,
April 2002.
[54] N. Yee et al., Multicarrier CDMA in Indoor Wireless Networks, in proc. IEEE PIMRC,
Yokohama, Japan, September 1993, pp. 109113.
[55] M. Jankiraman, Wideband Multimedia Solution Using Hybrid OFDM/CDMA/SFH Tech-
niques, PhD Thesis, Aalborg University, Denmark, July 2000.
c
Aalborg University 2004 Technical Report: R-04-1002 Page 60
OFDM Based Wireless Standards
Muhammad Imadur Rahman
, Suvra Sekhar Das
,
Basak Can
, Anders Brdls Olsen
Center for TeleInFrastruktur (CTiF), Aalborg University
Neils Jernes Vej 12, 9220 Aalborg st, Denmark
Center for Indlejrede Software Systemer (CISS), Aalborg University
Frederik Bajers Vej 7B, 9220 Aalborg st, Denmark
e-mail: {imr|ssd|bc|abo}@kom.aau.dk;
Phone: +45 9635 8688
Start date: 13 February 2004
Internal Report Number: (Example:) R-04-1001
ISBN Number: (Example:) 87-90834-42-9
ISSN Number: (Example:) 0908-1224
c
Aalborg University 2004
Abstract
The goal is to describe the wireless standards based on Orthogonal Frequency Division Multi-
plexing (OFDM) technology. This report is intended to provide an overview of the present state
of OFDM based wireless systems with respect to physical layer issues, so that a complete un-
derstanding of dierent OFDM system design issues are easily understood. The current WLAN
standards (IEEE 802.11a in USA, HiperLAN/2 in Europe and MMAC in Japan) and WMAN
standard (IEEE 802.16a) are all based on OFDM in their PHY layer. Upcoming standards, like
IEEE 802.20 and IEEE 802.11n, will also most likely follow the suit.
It is worth mentioning here that the explanation on various OFDM based standards presented
here are in no way a complete description. For details, it is suggested to study the references
that are mentioned in this report.
Contents
Table of Contents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ii
List of Figures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii
List of Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv
1 Introduction 1
1.1 OFDM for Future Wireless Systems . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Organization of The Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2 Digital Audio Broadcasting(DAB) 4
2.1 DAB System Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3 Digital Terrestrial Video Broadcast(DVB-T) 8
4 IEEE 802.11a, HiperLAN/2 and MMAC 9
4.1 OFDM Parameter Choice for IEEE 802.11a PHY Functionality . . . . . . . . . . 10
4.2 Channel Coding and Interleaving in IEEE 802.11a . . . . . . . . . . . . . . . . . 11
4.3 IEEE 802.11a Frame Structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
5 IEEE 802.20 14
6 IEEE802.16a 17
6.1 WirelessMAN-OFDM PHY Layer . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
6.1.1 Symbol Parameter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
6.1.2 Frame Structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
6.1.3 Channel Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
6.1.4 Control Mechanism . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
6.1.5 Transmitter/Receiver Parameters . . . . . . . . . . . . . . . . . . . . . . . 20
6.2 WirelessMAN-OFDMA PHY Layer . . . . . . . . . . . . . . . . . . . . . . . . . . 20
6.2.1 Symbol Parameter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
6.2.2 Frame Structure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
6.2.3 Channel Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
6.2.4 Control Mechanism . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
6.2.5 Transmitter/Receiver Parameters . . . . . . . . . . . . . . . . . . . . . . . 20
7 IEEE 802.11n (tracing its progress) 21
8 Conclusion 23
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page i
Reference 23
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page ii
List of Figures
1.1 Graphical Look at the Data Rate, Mobility and Coverage Range of Existing
WLANs, HomeRF and Bluetooth . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.1 General block diagram of the DAB system [?] . . . . . . . . . . . . . . . . . . . . 5
2.2 DAB frame format [?] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
4.1 IEEE 802.11a Frame Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
4.2 IEEE 802.11a Pre-amble Structure . . . . . . . . . . . . . . . . . . . . . . . . . . 12
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page iii
List of Tables
2.1 Features of DAB Standard . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.1 Some Transmission Related Parameters of DVB-T Standard . . . . . . . . . . . . 8
4.1 Summery of Characteristics of IEEE 802.11a, IEEE 802.11b and HiperLAN/2 . . 10
4.2 Physical Layer Characteristics for IEEE 802.11a . . . . . . . . . . . . . . . . . . 11
4.3 IEEE 802.11a OFDM PHY Modulation Techniques . . . . . . . . . . . . . . . . . 11
5.1 Expected PHY Parameters for IEEE 802.20 MBWA . . . . . . . . . . . . . . . . 15
6.1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
6.2 Channel coding for modulation. RS is Read-Solomon (outer code), CC is convo-
lutional code (inner code) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page iv
Chapter 1
Introduction
The history of wireless networking stretches farther back several decades. It was over fty
years ago, during World War II, when the United States Army rst used radio signals for data
transmission. This inspired researchers in 1971 at the University of Hawaii to create the rst
packet based radio communications network. ALOHANET, as it was named, was essentially the
very rst WLAN. This was the beginning of WLAN era.
With the advent of 3rd Generation (3G) wireless systems, it is expected that higher mobility
with reasonable data rate (up to 2Mbps) can be provided to meet the current user needs. 3G
promises a wire line quality of services via a wireless channel. Naturally 3G is not the end of the
tunnel; ever increasing user demands have drawn the industry to search for better solutions to
support data rates of the range of tens of Mbps. For wide area coverage, further expansions of 3G
systems are already a question of research in all over the world. Certainly the bit rate will be much
higher than 2Mbps for such a system, up to tens of Mbps [1]. For local area coverage, Wireless
Local Area Networks (WLANs), such as IEEE 802.11a, HiperLAN/2 or MMAC
1
standards are
capable of providing data rates up to 54 Mbps. Along with these three, there are few other
emerging short-range wireless applications available, such as Bluetooth, HomeRF, etc.
WLANs can potentially be a promising tool in dierent user environments, namely home,
corporate and public environment etc. WLANs are used to connect wireless users to a xed LAN
in corporate environments. A major WLAN application will be in public sectors, where WLAN
can be used to connect a user to the backbone network. Airports, hotels, high-rising oces, city
centers will be target area for such public WLAN usage.
A person-centered network can also be established, which is often termed as Wireless Per-
sonal Area Networks (WPAN). WPAN can be able to connect TV, refrigerator, home security
appliances, and sensors etc. WPAN, such as Bluetooth PAN, can facilitate a comfortable oce
by connecting the computer, printer, fax and other oce appliances without any wire. Wireless
Personal Area Networks refer to the short-range personal network concepts, which spread the
networking area towards the personal space surrounding a person. A person can communicate
with the devices attached to his body or within his personal space, and can seamlessly move
within the existing networks environment [2]. Due to WPANs functional behavior, they are very
closely associated with WLANs, and will be treated as such in future.
Like any other wireless system, there was a need for an industry standard devised to ensure
the compatibility and reliability among all manufacturers of the devices, so that the WLANs are
1
IEEE802.11a is an USA-standard, HiperLAN/2 is a European standard and MMAC is developed in Japan.
All three of the standards are almost similar in their PHY layer.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 1
Bluetooth
HomeRF
IEEE 802.11a
IEEE 802.11b
0.5
1.0
2.0
11
54
Data rate
in Mbps
10 30
100
Range in meters
Mobility
Moderate
High
Low
Figure 1.1: Graphical Look at the Data Rate, Mobility and Coverage Range of Existing WLANs,
HomeRF and Bluetooth
widely accepted. There are quite a few standards for wired and wireless communication networks
that use the principles of Discrete Multi Tone (DMT) modulation and OFDM. Starting from
xed DSLs, there are broadcasting systems such as DAB and DVB-T and WLANs such as IEEE
802.11a, MMAC and HiperLAN/2 use OFDM as the core PHY technology. The latest wireless
standard based on OFDM is the IEEE 802.16a for Fixed Broadband Wireless Acess (FBWA)
system. Recently a new standard group IEEE 802.20 was formed to devise a new standard
for future Mobile Broadband Wireless Access (MBWA) system. The workgroup is considering
OFDM as the possible PHY solution. IEEE 802.20 promises very high mobility while providing
data rates to support multimedia applications.
1.1 OFDM for Future Wireless Systems
The nature of WLAN and WPAN applications demands high data rates. Multimedia communi-
cations, such as video transmission, can require high user data rate for good quality of viewing.
Naturally dealing with ever-unpredictable wireless channel at high data rate communications
is not an easy task. The idea of multi-carrier transmission has surfaced recently to be used
for combating the hostility of wireless channel. Orthogonal Frequency Division Multiplexing
(OFDM) is a special form of multi-carrier transmission where all the subcarriers are orthogonal
to each other. OFDM promises a higher user data rate transmission capability at a reasonable
complexity and precision.
At high data rates, the channel distortion to the data is very signicant, and it is some-
what impossible to recover the transmitted data with a simple receiver. A very complex receiver
structure is needed which makes use of computationally extensive equalization and channel es-
timation algorithms to correctly estimate the channel, so that the estimations can be used with
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 2
the received data to recover the originally transmitted data. OFDM can drastically simplify
the equalization problem by turning the frequency selective channel to a at channel. A simple
one-tap equalizer is needed to estimate the channel and recover the data.
Future telecommunication systems must be very ecient spectrally to support number of
users with high data rate. OFDM uses the available spectrum very eciently. This is very
useful for multimedia communications. Thus, OFDM stands a good chance to become the prime
technology for 4G. Pure OFDM or hybrid OFDM will be most likely the choice for physical layer
multiple access technique in the future generation of telecommunications systems.
1.2 Organization of The Report
In this report, we will briey introduce some of the standards mentioned above and we will
elaborately present IEEE 802.11a standard. We will also focus on forthcoming IEEE 802.20
BMWA system.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 3
Chapter 2
Digital Audio Broadcasting(DAB)
Until now, analog radio signals such as FM or MW have been subject to numerous kinds of
interference on their way from the transmitter to user radio. These problems were caused by
mountains, high-rise buildings and weather conditions. DAB, however, uses these eects as
reectors creating multipath reception conditions to optimize receiver sensitivity. Wide area
coverage is achieved with Single Frequency Networking (SFN). Since DAB always selects the
strongest regional transmitter automatically, a user will always be at the focal point of incoming
radio signals. DAB systems are capable of broadcasting several CD quality radio stations, data
and multimedia services in a time multiplex. Thus aside from distortion-free reception and CD
Quality sound, DAB oers further advantages as it has been designed for the multimedia age.
DAB can carry not only audio, but also text, pictures, data and even videos - all on a small
user radio [3]. DAB system provides reliable, multi-service broadcasting for reception by mobile,
portable and xed receivers.
In the following subsections, a brief introduction into the overall DAB system and the frame
structure is given.
2.1 DAB System Overview
In February 1995, European Telecommunication Standards Institute (ETSI) has established a
broadcasting standard for the Digital Audio Broadcasting (DAB) system for reception from
terrestrial or satellite transmitters in the Very High Frequency (VHF)/Ultra High Frequency
(UHF) frequency bands as well as for distribution through cable networks [?]. The general block
diagram of the transmission part of the DAB system is given in Figure 2.1. As shown on this
gure, DAB system contains three main signal-processing sub-systems [?]:
Audio Coding: Advanced audio compression techniques are applied.
Transmission Coding and Multiplexing: Data for a service, audio or independent data, must
be combined into a single data stream for transmission. This is known as multiplexing.
The conguration and content of the multiplex is totally under control of the broadcaster
and re-congurations can occur when required. The frame based multiplex contains three
distinct elements:
The Synchronization Channel conveys the frequency and timing information to allow
receivers to synchronize and to decode the DAB signals.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 4
The Fast Information Channel (FIC) carries the Multiplex Conguration Information
(MCI) and Service Information (SI), which describes the conguration within a multi-
plex, and informs receivers how to extract and decode the information for the service
selected by the user.
The Main Service Channel (MSC) comprises audio frames or data packets of the
services within the multiplex. This part of the multiplex carries essentially the useful
payload of the DAB multiplex.
COFDM modulation: The Coded Orthogonal Frequency Division Multiplexing (COFDM)
is a spectrally ecient multi-carrier digital modulation scheme, oering reliable reception
under hostile reception conditions such as multipath propagation [?]. In addition, COFDM
allows the intentional multipath, where all the transmitters within the SFN operate the
same frequency. These multipaths are constructive within the Guard Interval [?].
Figure 2.1: General block diagram of the DAB system [?]
Before transmission, convolutional forward-error-correction, channel coding and bit interleaving
are applied to each service to provide strong protection against bit-errors. This is important
in the environment where interference and multipath propagation would lead to both at and
frequency selective fading of the received signal spectrum.
The frame structure of the OFDM signal is given in Figure 2.2. MSC carries the useful payload
including the services supported by the system and it has a capacity of 55296 transmitted at
every 24 ms [?].
Some of the benets and opportunities stated previously can be summarized as [?]:
Reliable interference-free reception: The DAB system is resistant to the eects of multipath
propagation and interference, which would degrade reception of existing analogue services.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 5
Figure 2.2: DAB frame format [?]
Ecient use of the limited RF spectrum: A number of dierent services can be supported
within the same RF bandwidth. The use of single-frequency networks (SFNs), where all
the transmitters operate on the same radio frequency, allows a radio signal to convey
a multiplex including audio, multimedia or voice call services, using a single frequency,
throughout a large geographical area. SFNs are highly ecient in terms of the utilizing the
scarce spectrum that is available for broadcasting. Since all the transmitters for a given
multiplex operates on the same frequency, there is no need for a user re-tune its radio while
on the move in order to follow a service within the service area of the broadcaster.
Flexibility and choice: A wide range of services can be supported by the system, including
audio based services; existing services with improved features, such as text information,
graphics or multimedia; entirely new services, such as independent data services, multime-
dia applications.
Table 2.1 shows the main properties of DAB standard.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 6
Protocols Eureka 147 in Europe, Canada and Asia
IBOC in United States
ISDB in Japan.
Carrier Frequency 200 MHz, 700 MHz, 1.5 GHz
and 3 GHz
Transmission Bandwidth 1.536 MHz
Channel Data Rate 2.4 Mbps (after encoding)
Transmission Technique Coded OFDM (COFDM)
No. of Subcarriers 700
Symbol Mapping Dierential Quadrature Phase
Shift Keying (DQPSK)
Channel Coding Reed Solomon and Conventional codeing
Others Time-Frequency Interleaving
Usage of guard interval to prevent ISI
Table 2.1: Features of DAB Standard
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 7
Chapter 3
Digital Terrestrial Video
Broadcast(DVB-T)
DVB technology has become an integral part of global broadcasting, setting the global standard
for satellite (DVB-S), cable (DVB-C) and terrestrial(DVB-T) transmissions and equipment. In
DVB schemes, multiple high quality programs can be broadcasted within the same single fre-
quency band (i.e. TV, Music, Data). DVB-T uses COFDM scheme for transmission, so we will
concentrate on DVB-T in this subsection. IN DVB-T, mostly MPEG2 streams are transmitted.
DVB-T is the youngest of the three core DVB systems and the most sophisticated. Based on
COFDM and QPSK, 16 QAM and 64 QAM modulation, it is the most sophisticated and ex-
ible digital terrestrial transmission system available today. DVB-T allows services providers to
match, and even improve on, analog coverage, at a fraction of the power. It extends the scope
of digital terrestrial television in the mobile eld, which was simply not possible before, or with
other digital systems [4]. Some transmission related parameters of DVB-T is presented in Table
3.1.
Channel Bandwidth 5.71MHz ,6.66MHz or 7.61 MHz
Data Rate 3.732-23.751Mbps, 4.354-27.71Mbps, 4.98-31.67Mbps
Symbol Mapping 16-QAM
Channel Coding Reed-Solomon
No. of Subcarriers Mode 2k (193 pilots & 1512 data, so 1705 in total)
Mode 8k (769 pilots & 6048 data, so 6817 in total)
Table 3.1: Some Transmission Related Parameters of DVB-T Standard
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 8
Chapter 4
IEEE 802.11a, HiperLAN/2 and
MMAC
We will discuss IEEE 802.11a related issues in detail in this section. The IEEE 802.11 specica-
tion adopts four dierent physical layer implementations [5]. They are:
1. Direct Sequence Spread Spectrum (DSSS)
2. OFDM
3. Frequency Hopping Spread Spectrum (FHSS)
4. Infra Red (IR)
Out of these four, an extension of DSSS and OFDM are used in IEEE 802.11b and IEEE
802.11a respectively.
IEEE802.11a OFDM PHY delivers up to 54Mbps data rates in the 5GHz band. This band
provides 300 MHz of total bandwidth, 3 bands of 100MHz at 5.15-5.25 GHz, 5.25-5.35GHz and
5.725-5.825GHz. The OFDM physical layer is likely to become the basis for high-speed WLANs
as 802.11a products are already available in late 2001 and early 2002 [6].
HiperLAN/2 standard also uses OFDM as the physical layer standard. Table 4.1 summarizes
characteristics of IEEE 802.11a, 802.11b and HiperLAN/2 standard [1]. The features of IEEE
802.11b is also included in the table to show the stunning dierences of OFDM capabilities for
providing much higher user data rate compared to CDMA systems.
From Table 4.1, it is clear that IEEE 802.11a and HiperLAN/2 do not have much dierence in
their physical layer. Their main dierences lie between the standards corresponding to the higher-
level network protocols used. These two standards were designed for indoor environment, where
the coverage area is very small compared to wide area cellular systems. Typical applications of
these can be in hot-spot areas, such as airport, shopping malls, universities, city centers, etc,
where usually large numbers of people gather almost every part of the day.
Apart from 802.11a and 802.11b subgroup of IEEE 802.11 workgroup, there are few other
subgroup. They are IEEE 802.11 e, g, h and i. IEEE 802.11e provides Quality of Service (QoS)
support for OFDM based LAN applications, which will be critical for delay-sensitive applications
such as Voice over Wireless IP (VoWIP). The standard will provide classes of service with man-
aged levels of QoS for data, voice, and video applications. IEEE 802.11g uses OFDM modulation
as does 802.11a, but, for backward compatibility with 802.11b, it also supports Complementary
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 9
Code Keying (CCK) modulation and, as an option for faster link rates, allows Packet Binary
Convolutional Coding (PBCC) modulation. IEEE 802.11h standard is supplementary to the
MAC layer to comply with European regulations for 5GHz WLANs, such as 802.11a. IEEE
802.11i deals with security issues of OFDM WLANs. It describes the encrypted transmission of
data between systems of 802.11a and 802.11b WLANs. 802.11e is already issued and work on
802.11g, 802.11h and 802.11i are still on going.
802.11b 802.11a HiperLAN/2
Spectrum(GHz) 2.4 5.2 5.2
Modulation Technique DSSS OFDM OFDM
Max Physical 11 54 54
Rate(Mbps)
Max Data Rate, 5 32 32
layer 3 in Mbps
Medium Access CSMA/CA
1
CSMA/CA TDMA/TDD
2
Control
Connectivity Connectionless Connectionless Connection
oriented
Table 4.1: Summery of Characteristics of IEEE 802.11a, IEEE 802.11b and HiperLAN/2
From Table 4.1 it is clear that IEEE 802.11a and HiperLAN2 do not have much dierence in
their physical layer. Their main dierences lie between the standards corresponding to the higher-
level network protocols used. These two standards were designed for indoor environment, where
the coverage area is very small compared to wide area cellular systems. Typical applications of
these can be in hot-spot areas, such as airport, shopping malls, universities, city centers, etc,
where usually large numbers of people gather almost every part of the day.
4.1 OFDM Parameter Choice for IEEE 802.11a PHY Function-
ality
As this WLAN system is designed for indoor wireless access, the design criteria are always
streamlined to satisfy respective needs. Most indoor oce buildings experience 40-70ns of delay
spread, though this can go up to 200ns for certain environments. As a common guideline, the
guard period is chosen to be four times maximum delay spread, which is 800ns [5]. A practical
choice for symbol duration is at least ve times the guard time. IEEE 802.11a matches with
this choice as 4s. Other key parameters are mentioned in Table 4.2 [7]. The dierent data
rate support of IEEE 802.11a is possible by using dierent symbol mapping and channel coding
schemes. We placed a description of the channel coding options that the satndard provides
in Table 4.3. The use of a 20 MHz operating channel allows for reasonable speeds on each
channel (up to 54 Mbps), as well as a reasonable number of operating channels in the assigned
spectrum. OFDM splits an information signal across 52 separate subcarriers. Four of them are
pilot subcarriers that system uses as a reference to disregard the frequency or phase shifts of
1
Carrier Sensed Multiple Access/Collision Avoidance
2
Time Division Multiple Acess/Time Division Duplex
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 10
Parameter Value
Data rate 6, 9, 12 , 18 , 24 , 36 , 48 , 54 Mbps
Channel Spacing 20 MHz
IFFT used for 20 MSPS 64
Data Subcarriers 48
Pilot Subcarriers 4
Null Subcarriers 12
Carrier Spacing (F
c
) 20 MHz/64 = 312.5kHz
Nominal Bandwidth 312.5kHz*(48+4) = 16.25 MHz
Useful Symbol Period 1/ F
c
= 1/312.5kHz = 3.2s
Guard Period 0.8 s
Modulation schemes BPSK, QPSK, 16-QAM, 64-QAM
Coding Rate
1
2
,
2
3
,
3
4
Table 4.2: Physical Layer Characteristics for IEEE 802.11a
the signal during transmission. A pseudo-binary sequence is set through the pilot subcarriers
to prevent the generation of spectral lines [6]. The remaining 48 subcarriers provide separate
wireless pathways for sending the information in a parallel fashion.
4.2 Channel Coding and Interleaving in IEEE 802.11a
Data Modulation Coding Coded Code bits Data bits
rate scheme rate bits per per OFDM per OFDM
(Mbps) subcarrier symbol symbol
6 BPSK
1
2
1 48 24
9 BPSK
3
4
1 48 36
12 QPSK
1
2
2 96 48
18 QPSK
3
4
2 96 72
24 16-QAM
1
2
4 192 96
36 16-QAM
3
4
4 192 144
48 64-QAM
2
3
6 288 192
54 64-QAM
3
4
6 288 216
Table 4.3: IEEE 802.11a OFDM PHY Modulation Techniques
Experiences show that basic OFDM system is not able to obtain a BER of 10
5
or 10
6
without channel coding. Thus, all OFDM systems now a day are converted to COFDM. The
benets of COFDM are two-fold in terms of performance improvement. According to Table 4.3,
IEEE 802.11a standard oers wide variety of choices for coding and modulation, this allows a
chance of making trade-os for lot of considerations. The standard enables several data rates
by making use of dierent combinations of modulation and channel coding scheme. It is worth
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 11
P R E A M B L E
S I G N A L
G
I
G
I
G
I
G
I
D A T A D A T A
Pilots (Amplitde +/-1)
Zero (Amplitude 0 )
Data Sub-carrier
S
U
B
C
A
R
R
I
E
R
S
0
N-1
Time
Figure 4.1: IEEE 802.11a Frame Format
Figure 4.2: IEEE 802.11a Pre-amble Structure
mentioning here that the standard demands all 802.11a complaint products to support all the
data rates. Table 4.3 presents the dierent arrangement of modulation and coding scheme that
are used to obtain the data rates [6].
4.3 IEEE 802.11a Frame Structure
We describe the IEEE802.11a [7] frame format as described in Figure 4.1.
A transmitted packet has an all pilot (known data at Transmitter (Tx) and Receiver (Rx))
training sequence known as PREAMBLE at its beginning. It is used for packet start identi-
cation, automatic gain control system, symbol timing synchronization, initial carrier frequency
synchronization and channel estimation. WLAN standards such as IEEE 802.11a and Hiper-
LAN/2 species a preamble signal at the beginning of the transmission as shown in Figure 4.2.
In both the standards, the preambles are designed such that the start of the symbols can be
easily determined at the beginning of the transmission. The rst 10 parts starting from A
1
to
A
10
are all short training symbols; all of them are 16 samples long. The last two parts C
1
and C
2
are long training symbols that span 64 samples as it is for a regular OFDM symbol. The middle
part CP is 32 samples long and saves the long training symbols from multipath interferences.
The knowledge of the preamble is available to WLAN receiver, thus it can easily make use of
a simple cross-correlation technique for symbol timing. After the packet detection algorithm
signals the start of a packet, the symbol timing algorithm renes the estimation to sample level
precision.
A Guard Interval (GI ) follows the PREAMBLE which in turn is followed by the SIGNAL
eld. The SIGNAL eld has information about the packet length and modulation format used in
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 12
the frame. It is a Binary Phase Shift Keying (BKSP) modulated OFDM symbol. Then follows a
sequence of DATA elds separated by GIs, i.e the OFDM symbols carrying information. There
are 64 subcarriers used in the Fast Fourier Transform (FFT) block of the OFDM system under
consideration. Not all subcarriers are used to carry information. Some subcarriers such as the
zero frequency component (to avoid carrier transmission) and the higher frequency subcarriers
are made zero in order to avoid the ltering eect on the subcarriers due to analogue components.
Hence only 52 subcarriers carry non-zero power, among which, pilots tones (values 1) are present
at four distinct locations (subcarriers -21,-7,7 and 21). Thus only 48 subcarriers carry data
information. These subcarriers are modulated using Quadrature Amplitude Modulation (QAM).
All subcarriers have the same modulation scheme.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 13
Chapter 5
IEEE 802.20
The scope of IEEE 802.20 as per the draft so far available is, Specication of physical and
medium access control layers of an air interface for inter-operable mobile broadband wireless
access systems, operating in licensed bands below 3.5 GHz, optimized for IP-data transport, with
peak data rates per user in excess of 1 Mbps. It supports various vehicular mobility classes up
to 250 Km/h in a MAN environment and targets spectral eciencies, sustained user data rates
and numbers of active users that are all signicantly higher than achieved by existing mobile
systems. Its Goal is to enable world wide deployment of aordable, ubiquitous, always-on and
inter-operable multi-vendor Mobile Broadband Wireless Access (MBWA) networks that meet the
needs of business and residential end user markets. This aims to allows applications including,
but not limited to, full screen video, full graphic web browsing, e- mail, le upload and download
without size limitations (e.g., FTP), video and audio streaming (VOIP), IP Multicast, Telematics,
Location based services, VPN connections, VoIP, instant messaging and on- line multiplayer
gaming [8].
The system architecture is being planned to be a point to multipoint system that works from
a base station to multiple devices in a non-line of sight outdoor to indoor scenario.The system
must be designed to enable a macro-cellular architecture with allowance for indoor penetration
in a dense urban, urban, suburban and rural environment. Adaptive modulation and coding
shall also be used in order improve the quality of service.
Some of the desired system performance requirements are shown in Table 5.1.
For example, FEC codes such as Turbo codes or Low Density Parity Codes (LDPC) can give
10
2
frame error rate using
1
2
rate coding in a binary AWGN channel. Target frequency reuse
factor could be one meaning re-using all frequencies can be used in all cells and sectors. It is
currently being discussed that adaptive antennas could be used to achieve even better result.
The standard suggests that the Air Interface (AI) should support more than 100 active
(On or Hold state) users per sector/cell. The number of inactive (Sleep state) users may be
large and essentially unlimited.
As for the CHANNEL MODELS, there are dierent models being proposed. But a model
that may cater to both SISO and MIMO needs to be developed. Mainly three types of test
environments are specied, viz. indoor,Pedestrian and Vehicular. With each test environment,
for SISO, are associated three characteristics, viz. Path loss expression, Shadow fading expression
and measured delay spread characteristics. These characteristics are well captured in the draft .
The suggested mobility rates associated with these test environments are 0-3 kmph for indoor; 0-
10 for pedestrian; 0, 30, 120 and 250 kmph for vehicular mobility. Motorolla has also contributed
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 14
Mobility Vehicular mobility classes
up to 250 kmph (as
dened in ITU-R M.1043-1)
Sustained spectral eciency > 1 b/s/Hz/cell
Peak user data rate > 1 Mbps
(Downlink -DL)
Peak user data rate > 300 Kbps
(Uplink - UL)
Peak aggregate data rate > 4 Mbps
per cell (DL)
Peak aggregate data rate > 800 Mbps
per cell (UL)
Air Link MAC < 10msec
frame RTT
Channel Bandwidth 1.25 MHz / 5 MHz
Operating Frequency 3.5 MHz
Access TDD/FDD
Spectrum Allocations Licensed spectrum allocated
to mobile service
Secutrity Support Advanced Encryption Standard
Table 5.1: Expected PHY Parameters for IEEE 802.20 MBWA
a typical urban environment channel model.
When it comes to MIMO there is yet a consensus to be reached. MIMO channel models
build on the classical understanding of multi-path fading and Doppler spread by incorporating
additional concepts such as angle spread, angle of arrival, Power-Azimuth-Spectrum (PAS), and
the physical geometry of scattering objects in the vicinity of MIMO antenna array [9]. A MIMO
channel model must capture all the essential channel characteristics, including
1. Spatial characteristics (Angle Spread, Power Azimuth Spectrum, Spatial correlations);
2. Temporal characteristics (Power Delay Prole) and
3. Frequency-domain characteristics (Doppler spectrum).
In MIMO systems, the spatial (or angular) distribution of the multi-path components is
important in determining system performance. System capacity can be signicantly increased
by exploiting rich multi-path scattering environments.
There are three main approaches to MIMO channel modelling: the correlation model, the
ray-tracing model, and the scattering model. We have to watch carefully to which direction the
MIMO channel model converges.
Denitely antenna diversity and smart antennas are necessary for such a mobile environment.
It is somewhat clear that OFDM has to be used to counter the adverse multi-path eects at
such high data rate and such high mobility requirement. Due to doppler shift under very high
subscriber velocity, there may be a need to use more pilots in the OFDM frame than current
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 15
WLAN OFDM frame, thus the overhead will increase. So it is still a burning issue on what
should be the modulation technique for such MBWA system. Adaptive PHY layer could be
an optimal situation where the system may switch from one PHY to another PHY to suit the
channel conditions. In such a situation advanced hardware design is needed where switching from
one system to another does not include much overhead or have a considerable switching time.
Space-Time-Frequency Block Codes (STFBC) could be the coding scheme used in case of MIMO
systems. In a nutshell, lot of issues related AI design are still open for the nal implementation
of the standard.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 16
Chapter 6
IEEE802.16a
Since 1998 the IEEE 802.16 Working Group has prepared various standard proposals for Wire-
less Metropolitan Area Networks (MAN). The object of IEEE 802.16 is to dene a Broadband
Wireless Access (BWA), utilizing the point to multipoint access, addressing the rst/last mile
WirelessMAN network. The driving force is to nd alternatives to cabled solutions, such as coax-
ial systems, bre optics, which is a costly infrastructure deployed to individual subscribers. The
idea of WirelessMAN technology is to bring the network access to the building and use Wireless-
LAN or LANs to connect user to the network. However the design allows that the technology
directly access the users, also allowing support for nomadic or even slow moving users.
The initial interest was the 10-66 GHz band, in early 2000 it was extended to 2-11 GHz,
completed in 2001 and published in 2002 as the IEEE 802.16a standard.
The 10-66 GHz is designed as an LOS, with a single carrier air interface. It is a point-to-
multipoint technology, basically transmitting a TDM signal, with subscribers divided in time
slots. The DL and UL is either divided by TDD or FDD; transmitting at the same frequency
but not simultaneously, or transmitting in dierent frequency channels simultaneously (it can
though also transmit time-divided, allowing for less expensive devices), respectively.
The IEEE 802.16a for the 2-11 GHz uses a common basic MAC layer, with four dierent
PHY layer denitions:
WirelessMAN-SCa: a Single Carrier technology designed for NLOS, within the 2-11 GHz
band. For licensed bands with bandwidths provisioned dived by any power of two, but no
less than 1.25MHz.
WirelessMAN-OFDM: an Orthogonal Frequency Division Multiplexing technology designed
for NLOS. In overall is it comparable with 802.11a, though using a FFT size of 256 sub-
carriers.
WirelessMAN-OFDMA: an Orthogonal Frequency Division Multiple Access technology de-
signed for NLOS.
WirelessHUMAN: a High-Speed Unlicensed Metropolitan Area Network. The band is from
5-6 GHz divided into channels of 5 MHz, provided with an 8-bit unique number. It should
be noted that the 802.11a is also allocated within this band.
In the chapter only the WirelessMAN-OFDM and WirelessMAN-OFDMA will be described, with
the main focus on the WirelessMAN-OFDMA, as Wireless-OFDM is somewhat alike the 802.11.
The chapter will only concentrate on the PHY layer parameters, for the two selected denitions.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 17
6.1 WirelessMAN-OFDM PHY Layer
6.1.1 Symbol Parameter
In time domain the symbol is dened by the symbol time T
b
, the Cyclic Prex (CP) with time
T
g
and total symbol time T
s
. See Figure ?? for a symbol illustration.
!! insert 128aa from 802.16a !!
The BS and SS must use the same CP length for both DL and UL, and when a specic CP
is selected by the BS a change will require a resynchronization of the SS to the BS.
In the frequency domain the symbol is described by carriers, determined by the FFT size.
The carrier types are:
Data carriers: data transmitters
Pilot carriers: estimation purpose
Null carriers: guard bands and DC carrier
Parameter denitions of the OFDM symbol are:
BW: channel bandwidth
(F
s
/BW): ratio between sampling frequency and channel bandwidth
(T
g
/T
b
): ratio between CP time and symbol time (useful time)
N
FFT
: points in the FFT, number of carriers
Where the following parameters are derived:
Sampling frequency: F
s
= (F
s
/BW)BW
Carrier: f = f
s
/N
FFT
Useful time: T
b
= 1f
CP time: T
g
= (T
g
/T
B
)T
b
OFDM Symbol Time: T
s
= T
b
+T
g
Sample time: 1/F
s
The transmitted OFDM symbol is specied by:
s(t) = Re
e
j2f
c
t
N
used
/2
k=N
used
/2
c
k
e
j2kf(tT
g
)
, 0 < t < T
s
(6.1)
c
k
is the data to be transmitted, specied by a constellation point (QAM)
The individual parameter are specied as
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 18
Parameter Value
N
FFT
256
N
used
200
Lower guard carriers 28 at carrier {-128,127,...,-101}
Higher guard carriers 27 at carrier {101,102,..,127}
(T
g
/T
b
) 1/4, 1/8, 1/16, 1/32
Table 6.1:
6.1.2 Frame Structure
6.1.3 Channel Coding
Channel coding is composed of three steps; randomizing, forward error correction and interleav-
ing. The operations are made in this order at transmission and in reverse order at reception.
The randomizing is only performed on data bits, preambles are not randomized. Randomizing
is made of DL and UL, performed on an OFDM symbol only. If data is not tting the data carriers
allocated it is padded using locical 1s. The randomizing is performed using the generator shown
in Figure ??, where the randomizer is reinitialized at each frame.
!!insert gure 128ac !!!
Forward error correction is combination of a Reed-Solomon outer code and a rate-convolutional
inner code, both for DL and UL. In Table 6.1.3 the options for channel coding is listed, in ex-
tension there is also a option for making Block Turbo Codes.
Modulation Uncoded block Coded block Overall RS code CC code rate
size (byte) size (byte) coding rate
QPSK 24 48 1/2 (32, 24, 4) 2/3
QPSK 36 48 3/4 (40, 36, 2) 5/6
16-QAM 48 96 1/2 (64, 48, 8) 2/3
16-QAM 72 96 3/4 (80, 72, 4) 5/6
64-QAM 96 144 2/3 (108, 96, 6) 3/4
64-QAM 108 144 3/4 (120, 108, 6) 5/6
Table 6.2: Channel coding for modulation. RS is Read-Solomon (outer code), CC is convolutional
code (inner code)
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 19
6.1.4 Control Mechanism
6.1.5 Transmitter/Receiver Parameters
6.2 WirelessMAN-OFDMA PHY Layer
6.2.1 Symbol Parameter
6.2.2 Frame Structure
6.2.3 Channel Coding
6.2.4 Control Mechanism
6.2.5 Transmitter/Receiver Parameters
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 20
Chapter 7
IEEE 802.11n (tracing its progress)
The original IEEE study group, which is now called IEEE 802.11n standard committee, was
known as High Throughput Study Group and was to report to the IEEE 802.11 Working Group.
This group started during September 2002. The approval of the IEEE 802.11n was done in July
2003 and they had their rst ocial meeting in September 2003. The scope of the project was:
To dene standardized modications to the 802.11 MAC and PHY layers that achieve a mini-
mum increase (xx) in throughput as measured at the MAC data SAP. The purpose: To improve
the 802.11 wireless LAN user experience by providing signicantly higher throughput for current
applications and to enable new applications and market segments [10]. The proposed title for
the project as per September meeting was: Proposed probable title Amendment to STANDARD
[FOR] Information Technology-Telecommunications and information exchange between systems-
Local and Metropolitan networks-Specic requirements-Part 11: Wireless LAN Medium Access
Control (MAC) and Physical Layer (PHY) specications: Enhancements for Higher Eective
Throughput
The target schedule as per September was as follows:
Sep 2002 - 5 Criteria and PAR started
Nov 2002 - Request for creation of Task Group to be sent to Executive Committee with 5 Criteria
and PAR
Jan 2003 - Technology solutions presented in earnest -Requirements doc complete.
Mar 2003 - Technology Solutions presented
May 2003 - Selection of Solution and start writing Draft
Jul 2003 - Complete initial draft and send out 1st WG Letter Ballot
Sep 2003 -process comments and send 2nd WG Letter Ballot
Nov 2003 - Comment resolution and start recirculation LB
Jan 2004 - nal resolution of comments
Mar 2004 - Send to Sponsor Ballot
May 2004 - Resolve comments o July 2004 - Send to Revcom
The target of this project is to enhance the MAC and the PHY to achieve data rates
more than 100 mbps. It targets to improve spectral eciency, extend the range by atleast
1.5 times,ultimately to enhance the wireless access experience of the end user.
It is planned to operate in the 5 GHz spectrum. The networking mode is to provide Ecient
support of both centralized, Peer to Peer and ad Hoc networking mode. Provide ecient support
low bit rate applications example voice.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 21
The technical avenues being considered are: OFDM with higher number of sub-carriers
and higher order QAM, Space-time coding techniques(2X2 MIMO)[11], New channel coding
techniques(- e.g. low constraint length turbo-codes),Hybrid ARQ(Incremental Redundancy (IR)
and Chase Combining), MAC eciency improvement(TDD/TDMA incl. backward compatibil-
ity,Reducing overhead in the MAC will only be part of the story).
The channel models being studied are both SISO and MIMO. For SISO, the space is
being separated in to residential, oce, indoor-to-indoor, indoor-to-outdoor, and wall penetration
models. Model parameters oer path loss and delay spread expectations for a large percentage
of typical WLAN deployments. Propagation results have been used to dene model parameters
for the Channel Modeling Interest Group.[12]. MIMO models is still under development. The
important parameters for MIMO modeling being considered are:
Angular SpectraAngular spectra tie physical propagation models to MIMO system perfor-
mance.It includes information from where energy is arriving for determining received power into
antenna patterns. It also considers arrayed antenna correlation properties. It is closely related
to ray arrivals and scattering models.Scaterers need be considered if present.
Channel Modelling Interest Group are developing a model based on clusters of scatterers. As-
sumptions are made regarding number, size, and time-of-arrival characteristics both in aggregate
and with 10 ns range resolution.
Extracts from results of experiments[11] [12]shows that Spectra from horizontally oriented
antennas show a strong collimation of signal energy between the oor and the ceiling. o Number
of scattering clusters contributing to the signal energy can depend on the time delay investigated.
o Generally more clusters enter into the scattering process as the time of arrival increases.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 22
Chapter 8
Conclusion
We gave a brief overview of OFDM based wireless systems in this report. A signicant moment
for OFDM technology is its success in IEEE 802.11a system. IEEE 802.11a and HiperLAN/2
standards are capable of providing user data rates up to 54Mbps, where as the mobility is very
limited. This is because of the nature of the system, where local area coverage was targeted, so
only indoor scenarios are taken into account while devising the standards. For future wide-area
4G systems based on OFDM or hybrid OFDM, Doppler eects which is related to high mobility
(or vehicular use), must be kept in consideration. For enhancing the data rate and improving the
link performance, space-time coding or MIMO modelling can be incorporated with the current
WLANs.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 23
Bibliography
[1] E.P. Lawrey, Adaptive Techniques for Multiuser OFDM, Ph.D. dissertation, James Cook
University, Australia, December 2001.
[2] R. Prasad & L. Gavrilovska, Research Challenges for Wireless Personal Area Networks,
in Proc. of 3
rd
International Conference on Information, Communications and Signal Pro-
cessing (ICICS), Singapore, October 2001.
[3] Internet, The World DAB Forum, web address: http://www.worlddab.org/.
[4] , The DVB Project, web address: http://www.dvb.org/.
[5] Matthew S. Gast, 802.11 Wireless Networks: The Denitive Guide, 1st ed. OREILLY,
April 2002.
[6] J. Geier, Wireless LANs, Implementing High Performance IEEE 802.11 Networks, 2nd ed.
Sams Publishing, July 2001.
[7] LAN/MAN Standards Committee of the IEEE Computer Society, Part 11: Wireless LAN
Medium Access Control (MAC) and Physical Layer (PHY) Specications-High speed Phys-
ical Layer in the 5 GHz Band, ANSI/IEEE Std 802.11, 1999.
[8] IEEE 802.20 Workgroup, IEEE 802.20 Requirements Document, Contribution to WG;
Doc. no. C802.20-03/69r1, 2003.
[9] , Channel Models for IEEE 802.20 MBWA System Simulations - Rev 02, Contribution
to WG; Doc. no. C802.20-03/79r2, 2003.
[10] Internet IEEE 802.20 Workgroup, IEEE 802.11n Workgroup, web address:
http://grouper.ieee.org/groups/802/11/.
[11] IEEE 802.11n Workgroup, HTSG Performance of Popular Space Time Codes in IEEE
802.11n System, Contribution to WG; Doc. no. C11-03-298r0, 2003.
[12] , SISO & MIMO Channel Propagation Results in WLAN System, Contribution to
WG; Doc. no. C11-03-313r0, 2003.
c
Aalborg University 2004 Technical Report: (Example:) R-04-1001 Page 24
You might also like
- OFDMDocument12 pagesOFDMNizashivaNo ratings yet
- OfdmDocument2 pagesOfdmArunkumar100% (2)
- Optimum Array Processing: Part IV of Detection, Estimation, and Modulation TheoryFrom EverandOptimum Array Processing: Part IV of Detection, Estimation, and Modulation TheoryNo ratings yet
- How To Guide On JPerf and IPerfDocument6 pagesHow To Guide On JPerf and IPerfDan MereanuNo ratings yet
- Mimo OfdmDocument20 pagesMimo OfdmNishad MuhammedNo ratings yet
- IEEE Bare Demo Template For ConferencesDocument4 pagesIEEE Bare Demo Template For ConferenceskailashNo ratings yet
- OFDM Basics TutorialDocument215 pagesOFDM Basics Tutorialtanujchawla30No ratings yet
- Study and Simulink For Performance of - Multi-Input Multi-Output (Mimo) by Using - Receiver Detection Algorithms PDFDocument104 pagesStudy and Simulink For Performance of - Multi-Input Multi-Output (Mimo) by Using - Receiver Detection Algorithms PDFmahmoud BiomyNo ratings yet
- VLSI Implementation OfdmDocument40 pagesVLSI Implementation Ofdmmanasverma21270% (1)
- Ergodic Capacity For MIMO LTEDocument15 pagesErgodic Capacity For MIMO LTENebiye SolomonNo ratings yet
- Point-To-Multipoint Network Design GuideDocument35 pagesPoint-To-Multipoint Network Design Guidemichiiro0% (1)
- A A Seminar Seminar On On: "Mimo Ofdm " "Mimo-Ofdm "Document23 pagesA A Seminar Seminar On On: "Mimo Ofdm " "Mimo-Ofdm "Arjun Nichal0% (1)
- (Date) : DheerajDocument22 pages(Date) : Dheerajazad Tech20No ratings yet
- OFDM Basics TutorialDocument3 pagesOFDM Basics Tutorialhisoni85No ratings yet
- 5g Ug PDFDocument26 pages5g Ug PDFypobuleshNo ratings yet
- OFDMDocument19 pagesOFDMNizashivaNo ratings yet
- Tutorial On MIMODocument61 pagesTutorial On MIMOHa GiangNo ratings yet
- MIMO TutorialDocument54 pagesMIMO TutorialSPSNo ratings yet
- Interpolation in Digital Modems. I. FundamentalsDocument7 pagesInterpolation in Digital Modems. I. FundamentalsNéstor O. Bayona A.No ratings yet
- Multi-Carrier Technologies For Wireless CommunicationDocument215 pagesMulti-Carrier Technologies For Wireless Communicationalansi92004100% (2)
- The LabVIEW Simulation of Space-Time Coding Technique in The MIMO-OfDM SystemDocument6 pagesThe LabVIEW Simulation of Space-Time Coding Technique in The MIMO-OfDM Systemivy_publisherNo ratings yet
- Visible Light CommunicationDocument16 pagesVisible Light CommunicationShirish MishraNo ratings yet
- Presentation OFDM ECM740Document21 pagesPresentation OFDM ECM740Byron FischerNo ratings yet
- Rake ReceiverDocument48 pagesRake ReceiverIk Ram100% (1)
- How To Design A GaN PA MMICDocument9 pagesHow To Design A GaN PA MMICJohn StewardNo ratings yet
- OFDM LectureDocument128 pagesOFDM Lectureashugolu02No ratings yet
- Presented By: Eng. Makarios Eshak Brnab Date: 1 November, 2017Document14 pagesPresented By: Eng. Makarios Eshak Brnab Date: 1 November, 2017Makarios Eshak BarnabNo ratings yet
- (Erik G. Larsson, Petre Stoica) Space-Time BlockDocument300 pages(Erik G. Larsson, Petre Stoica) Space-Time BlockGurpal SinghNo ratings yet
- 5G Simulation Framework: Junior Asante and Joel OlssonDocument110 pages5G Simulation Framework: Junior Asante and Joel OlssonmahaNo ratings yet
- Guided By:: Submitted By: Shuchi Jani Enrol - No. MU09MCS019Document30 pagesGuided By:: Submitted By: Shuchi Jani Enrol - No. MU09MCS019bhoop_sharmaNo ratings yet
- Sonet/sdh PDFDocument80 pagesSonet/sdh PDFRyanXuNo ratings yet
- Signal Processing and CommunicationsDocument38 pagesSignal Processing and CommunicationsoveiskntuNo ratings yet
- IQ RF MappingDocument14 pagesIQ RF Mappingsatcom_77No ratings yet
- Evolution Toward 5G Multi-Tier CellularDocument21 pagesEvolution Toward 5G Multi-Tier Cellulareshwar_worldNo ratings yet
- What's The Difference Between Broadband and Narrowband RF CommunicationsDocument8 pagesWhat's The Difference Between Broadband and Narrowband RF Communicationssameer_msbNo ratings yet
- Beamforming BasicsDocument6 pagesBeamforming BasicsRitika Jain0% (1)
- Horizon Quantum User Manual - Volume 1-83-000074-01!01!03Document90 pagesHorizon Quantum User Manual - Volume 1-83-000074-01!01!03curz100% (2)
- A Seminar Report On Mimo TechnologyDocument30 pagesA Seminar Report On Mimo TechnologyDurgesh JaiswalNo ratings yet
- BG 1Document1 pageBG 1bruck bogaleNo ratings yet
- Lte Ofdm, Ofdma and Sc-FdmaDocument5 pagesLte Ofdm, Ofdma and Sc-FdmaSamsher SinghNo ratings yet
- Free Space OpticsDocument25 pagesFree Space Opticsgssatishk629No ratings yet
- Software RadioDocument117 pagesSoftware Radiochocobon_998078100% (1)
- Digital CommunicationDocument220 pagesDigital Communicationrocko101100% (2)
- IVCAD MT930M1M2A OM HEMT ModelDocument65 pagesIVCAD MT930M1M2A OM HEMT ModellotfiNo ratings yet
- Lab 2 ZF MMSEDocument7 pagesLab 2 ZF MMSEGuillermo OlmosNo ratings yet
- Low Density Parity Check (LDPC) Coded MIMOConstantDocument4 pagesLow Density Parity Check (LDPC) Coded MIMOConstantkishoreNo ratings yet
- Hybrid CouplerDocument14 pagesHybrid CouplerSHAILESHNo ratings yet
- RII & RIF FiltersDocument13 pagesRII & RIF FiltersMedab Abd El MalekNo ratings yet
- Multi-Carrier Techniques For Broadband Wireless Communications (Man-On Pun) PDFDocument272 pagesMulti-Carrier Techniques For Broadband Wireless Communications (Man-On Pun) PDFAnonymous bZtJlFvPtpNo ratings yet
- An Overview of Research Topics and Challenges For 5G Massive MIMO AntennasDocument4 pagesAn Overview of Research Topics and Challenges For 5G Massive MIMO AntennasAnil Kumar BNo ratings yet
- Channel Coding Techniques For Wireless CDocument407 pagesChannel Coding Techniques For Wireless CAnirban HomroyNo ratings yet
- ch6 ModulatorsDocument84 pagesch6 ModulatorsAaron ThomasNo ratings yet
- EDFA Sim ModelDocument4 pagesEDFA Sim ModelRalph JohnsonNo ratings yet
- Digital ModulationDocument153 pagesDigital Modulationمحمود عبدالرحمن ابراهيمNo ratings yet
- Introduction To MIMO SystemsDocument14 pagesIntroduction To MIMO SystemsmazhaicNo ratings yet
- CH 9 Practice SolutionsDocument3 pagesCH 9 Practice SolutionsKarthik Mohan KNo ratings yet
- Turbo Coding and MAP Decoding: Intuitive Guide To Principles of Communications Charan LangtonDocument25 pagesTurbo Coding and MAP Decoding: Intuitive Guide To Principles of Communications Charan LangtonKarthik Mohan KNo ratings yet
- Solutions To Exercises in Chapter 8: 1.szm, xr8-1.wf1 and Xr8-1.sas, RespectivelyDocument12 pagesSolutions To Exercises in Chapter 8: 1.szm, xr8-1.wf1 and Xr8-1.sas, RespectivelyKarthik Mohan KNo ratings yet
- ECE531 Screencast 2.1: Introduction To The Cramer-Rao Lower Bound (CRLB)Document5 pagesECE531 Screencast 2.1: Introduction To The Cramer-Rao Lower Bound (CRLB)Karthik Mohan KNo ratings yet
- ECE531 Screencast 2.2: Fisher Information For Estimating A Scalar ParameterDocument7 pagesECE531 Screencast 2.2: Fisher Information For Estimating A Scalar ParameterKarthik Mohan KNo ratings yet
- GSM and Lte Network ArchitectureDocument12 pagesGSM and Lte Network ArchitectureKarthik Mohan KNo ratings yet
- Python Numpy Tutorial (CS231n-Stanford)Document27 pagesPython Numpy Tutorial (CS231n-Stanford)Karthik Mohan KNo ratings yet
- Bell Laboratories Layered Space TimeDocument3 pagesBell Laboratories Layered Space TimeKarthik Mohan KNo ratings yet
- ContohDocument7 pagesContohJiah Mohd DaudNo ratings yet
- Differences Between TDMA, CDMA, and FDMADocument1 pageDifferences Between TDMA, CDMA, and FDMAKarthik Mohan KNo ratings yet
- Correlation Model 4 Shadow Model in Mob Rad CommDocument2 pagesCorrelation Model 4 Shadow Model in Mob Rad CommKarthik Mohan KNo ratings yet
- Lecture3 - Small Scale FadingDocument24 pagesLecture3 - Small Scale FadingKarthik Mohan KNo ratings yet
- Papr in Ofdm SystemDocument3 pagesPapr in Ofdm SystemKarthik Mohan KNo ratings yet
- Multiple Access TechniquesDocument22 pagesMultiple Access TechniquesArun KumarNo ratings yet
- FDMADocument66 pagesFDMApoojapriya204100% (2)
- Coaxial Cable & Twisted Pair CableDocument14 pagesCoaxial Cable & Twisted Pair CableJasper ParkNo ratings yet
- Telit fn980fn980m DatasheetDocument2 pagesTelit fn980fn980m DatasheetkksdnjdaNo ratings yet
- Rugged Tablet: Features and BenefitsDocument2 pagesRugged Tablet: Features and BenefitsHussain MulthazimNo ratings yet
- DCS43PA05F10Document2 pagesDCS43PA05F10culeros1No ratings yet
- RF Based Railway Station Announcement SystemDocument3 pagesRF Based Railway Station Announcement SystemCrispNo ratings yet
- DbSpectra Catalog 17.2Document109 pagesDbSpectra Catalog 17.2michaelethompson100% (1)
- Thesis (Time Synchronization in Wireless Telecommunication) NewDocument50 pagesThesis (Time Synchronization in Wireless Telecommunication) NewParesh SawantNo ratings yet
- RF 7800s TR PDFDocument2 pagesRF 7800s TR PDFEdmond100% (1)
- Viva Voce Questions On Communication SystemsDocument3 pagesViva Voce Questions On Communication SystemsZealWolf100% (3)
- 2G Drive Test KPI Item Service Achieve Minimum Target ANDDocument9 pages2G Drive Test KPI Item Service Achieve Minimum Target ANDأبوعمر الفاروق عبدالرحمنNo ratings yet
- World Band Radio AR-1748: Owner'S ManualDocument16 pagesWorld Band Radio AR-1748: Owner'S ManualdarrelsilvaNo ratings yet
- Cisco 1100 Series SWCFG Chapter 01011 PDFDocument76 pagesCisco 1100 Series SWCFG Chapter 01011 PDFreferenceref31No ratings yet
- CH 03 Lattice ChartsDocument3 pagesCH 03 Lattice ChartsAmit PandeyNo ratings yet
- AC1200 Wireless Dual Band Gigabit Router: FeaturesDocument2 pagesAC1200 Wireless Dual Band Gigabit Router: FeaturesMarius-Florin NICULAENo ratings yet
- Block-Diagram Tour Late Model (5100 Series) EF Johnson 700/800 MHZ 2-Way Radio RF DeckDocument7 pagesBlock-Diagram Tour Late Model (5100 Series) EF Johnson 700/800 MHZ 2-Way Radio RF DeckJimNo ratings yet
- Design and Analysis of Tripple Band Koch Fractal Yagi Uda Antenna IJECW 2013Document5 pagesDesign and Analysis of Tripple Band Koch Fractal Yagi Uda Antenna IJECW 2013mahadiNo ratings yet
- JSS-296 - NCR-333 - Ton SART20 - Tron 40SDocument401 pagesJSS-296 - NCR-333 - Ton SART20 - Tron 40SBryan MilloNo ratings yet
- How Does The Doppler Radar WorkDocument2 pagesHow Does The Doppler Radar Workcats1298100% (1)
- Radio Wave Propagation FundamentalsDocument440 pagesRadio Wave Propagation FundamentalsyudiNo ratings yet
- U900 Training Session1Document20 pagesU900 Training Session1Zouhir El Allaoui100% (1)
- NCU NetworlControlUnit DataSheetDocument17 pagesNCU NetworlControlUnit DataSheetcasapvaNo ratings yet
- Nortel Fractional Reuse PlanningDocument17 pagesNortel Fractional Reuse PlanningWong_Hong_WeiNo ratings yet
- Design & Analysis of Microstrip Patch Antenna For 3g Applications 20.4.2014Document57 pagesDesign & Analysis of Microstrip Patch Antenna For 3g Applications 20.4.2014Fuad Adnan Rahmani100% (1)
- General Concept of Frequency HoppingDocument35 pagesGeneral Concept of Frequency Hoppinglovesstudy100% (1)
- HT700v2 Service ManualDocument93 pagesHT700v2 Service Manualcdiulio3128No ratings yet
- Communications QBDocument38 pagesCommunications QBDenaiya Watton LeehNo ratings yet
- DVX VHF Digital Voice Transceiver: Moe Wheatley, AE4JYDocument20 pagesDVX VHF Digital Voice Transceiver: Moe Wheatley, AE4JYPaulo FernandesNo ratings yet
- 1.4 Key Enabling Technologies and Features of LTE: 1.4.1 Orthogonal Frequency Division Multiplexing (OFDM)Document39 pages1.4 Key Enabling Technologies and Features of LTE: 1.4.1 Orthogonal Frequency Division Multiplexing (OFDM)rohan gowdaNo ratings yet
- Evaluation of Some Websites that Offer Virtual Phone Numbers for SMS Reception and Websites to Obtain Virtual Debit/Credit Cards for Online Accounts VerificationsFrom EverandEvaluation of Some Websites that Offer Virtual Phone Numbers for SMS Reception and Websites to Obtain Virtual Debit/Credit Cards for Online Accounts VerificationsRating: 5 out of 5 stars5/5 (1)
- Hacking: A Beginners Guide To Your First Computer Hack; Learn To Crack A Wireless Network, Basic Security Penetration Made Easy and Step By Step Kali LinuxFrom EverandHacking: A Beginners Guide To Your First Computer Hack; Learn To Crack A Wireless Network, Basic Security Penetration Made Easy and Step By Step Kali LinuxRating: 4.5 out of 5 stars4.5/5 (67)
- Microsoft Azure Infrastructure Services for Architects: Designing Cloud SolutionsFrom EverandMicrosoft Azure Infrastructure Services for Architects: Designing Cloud SolutionsNo ratings yet
- Cybersecurity: A Simple Beginner’s Guide to Cybersecurity, Computer Networks and Protecting Oneself from Hacking in the Form of Phishing, Malware, Ransomware, and Social EngineeringFrom EverandCybersecurity: A Simple Beginner’s Guide to Cybersecurity, Computer Networks and Protecting Oneself from Hacking in the Form of Phishing, Malware, Ransomware, and Social EngineeringRating: 5 out of 5 stars5/5 (40)
- AWS Certified Solutions Architect Study Guide: Associate SAA-C02 ExamFrom EverandAWS Certified Solutions Architect Study Guide: Associate SAA-C02 ExamNo ratings yet
- Microsoft Certified Azure Fundamentals Study Guide: Exam AZ-900From EverandMicrosoft Certified Azure Fundamentals Study Guide: Exam AZ-900No ratings yet
- Open Radio Access Network (O-RAN) Systems Architecture and DesignFrom EverandOpen Radio Access Network (O-RAN) Systems Architecture and DesignNo ratings yet
- The Compete Ccna 200-301 Study Guide: Network Engineering EditionFrom EverandThe Compete Ccna 200-301 Study Guide: Network Engineering EditionRating: 5 out of 5 stars5/5 (4)
- Cybersecurity: The Beginner's Guide: A comprehensive guide to getting started in cybersecurityFrom EverandCybersecurity: The Beginner's Guide: A comprehensive guide to getting started in cybersecurityRating: 5 out of 5 stars5/5 (2)
- ITIL® 4 Create, Deliver and Support (CDS): Your companion to the ITIL 4 Managing Professional CDS certificationFrom EverandITIL® 4 Create, Deliver and Support (CDS): Your companion to the ITIL 4 Managing Professional CDS certificationRating: 5 out of 5 stars5/5 (2)
- Palo Alto Networks: The Ultimate Guide To Quickly Pass All The Exams And Getting Certified. Real Practice Test With Detailed Screenshots, Answers And ExplanationsFrom EverandPalo Alto Networks: The Ultimate Guide To Quickly Pass All The Exams And Getting Certified. Real Practice Test With Detailed Screenshots, Answers And ExplanationsNo ratings yet
- Azure Networking: Command Line Mastery From Beginner To ArchitectFrom EverandAzure Networking: Command Line Mastery From Beginner To ArchitectNo ratings yet
- Set Up Your Own IPsec VPN, OpenVPN and WireGuard Server: Build Your Own VPNFrom EverandSet Up Your Own IPsec VPN, OpenVPN and WireGuard Server: Build Your Own VPNRating: 5 out of 5 stars5/5 (1)
- ITIL 4 : Drive Stakeholder Value: Reference and study guideFrom EverandITIL 4 : Drive Stakeholder Value: Reference and study guideNo ratings yet
- Digital Health: Mobile and Wearable Devices for Participatory Health ApplicationsFrom EverandDigital Health: Mobile and Wearable Devices for Participatory Health ApplicationsShabbir Syed-AbdulNo ratings yet
- AWS Certified Cloud Practitioner Study Guide: CLF-C01 ExamFrom EverandAWS Certified Cloud Practitioner Study Guide: CLF-C01 ExamRating: 5 out of 5 stars5/5 (1)