4 Unit Maths Complex Numbers

Complex Laws.

Let z1 = a + ib, and z2 = c + id, where a, b, c and d are real numbers.

z 1+ z 2=a+ib+ ( c+id )
z 1z 2=a+ib(c +id )
z 1 z 2=(a+ib)( c+id)
z 1 a+ib
=
z 2 c+ id

Square root of a
complex number.

z= a+ib
let z 2=a+ib
x 2 y 2 =a
xy=

b
2

Solve for x and y by inspection. If unable to do through inspection use the identity;
2

( x 2+ y 2) =( x 2 y 2 ) +4 x 2 y 2
And then perform simultaneous equations.
Conjugate.

If

z=x +iy

then

z =xiy

( z )=z
z 1+ z 2= z1 + z2
z 1z
2= z1 z2
z 1z 2= z1 z2

z1 z1
=
z2 z2

()
Adding vectors.

Complete Parallelogram

Head to Tail

V 1+ V 2
V1

V1

V 1V+1V+ 2V 2
V2

Thompson Ly
1

V2 V2

4 Unit Maths Complex Numbers

Subtracting vectors.

Complete Parallelogram

V2

V 1V 2
V1

V1

V 2V 1
V2

V 2
V 1+ (V 2)
V 1V 2
Modulus-Argument
form.

z=x +iy=r (cos+ isin)

Where ; r= x 2 + y 2tan=

If equation is not in correct

y
x
cos+ isin

, (eg,

cos isin

) use the unit circle

just think of when the two conditions are met.

Rules of Modulus.

The modulus of a complex number is its length.

If z1 =z2 , thenr 1=r 2

|z 1 z 2|=| z1||z 2|

||

z1 |z 1|
=
z2 |z 2|

|z n|=| z|n

|1z|=|1z|
|z|=| z|
2

z z =| z|

Rules of Argument.

The argument of a complex number is the angle made with respect to the positive xaxis.

If z1 =z2 , then1= 2+k 2

arg ( z 1 z 2 )=arg z 1+ arg z 2

Thompson Ly
2

4 Unit Maths Complex Numbers

z
arg 1 =arg z 1arg z2
z2

( )

arg zn =nargz
arg

( 1z )=argz

arg z =argz
Further vector
properties.

If tail is at the origin, only one letter is used.

However, if tail is not at origin, two letters are used.

AB=
B
A

Note: goes from A to B. The arrow starts at A and ends at B.

Angel between two
vectors.

Arg

AB
= Arg
AC Arg
BD (headtail)
BD

( )

Rules
Separate the argument like above.
Draw vectors z1 and z2.
Look at the heads of the vectors.A
Determine the direction of angle.
Note: angle is between the two heads, and the
head of the angle is on the head line.

D
Rotations.

To rotate a complex number, z, by

zcis

anticlockwise, multiply z by cis

Reducing/Enlarging.

To reduce/enlarge a complex number, by x, multiply z by x to get xz.

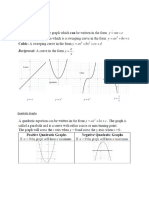
Purely real/imaginary.

Consider the complex number; z = x + iy.

Purely imaginary
When x = 0.

When

argz= +k .
2

Purely real
When y = 0.

Thompson Ly
3

When

argz=0+ k

to get

4 Unit Maths Complex Numbers

De Moivres Theorem.

(cos +isin) =cosn +isinn

(cosisin)n=cosnisinn

Trigonometry

Questions such as: Find cosnp in terms of powers of cos.

(cosp +isinp)n

Start off by writing:

On the left hand side of the equation, use De Moivres theorem, whilst on the
right hand side, expand normally using Pascals triangles.
Compare the real and imaginary parts, depending on question.

= ___

Questions such as: Find cosnx in terms of multiples of x.

Non-root of unity.

Root of unity.

z n+

1
=2 cosn
n
.
z

z n

1
=2 isinn
n
.
z

n
(2 cosx/sinx) =

Start off by writing:

Group powers of x with their inverse, and then use the two above
equations.
n

z =complex number (note: a real number is also complex)

In the form;

z n=( rcis)n

Here,

Turn the complex number into cis form, and then equate the equations.
n

z = 1

In the form;

z =( cis)

.
.

The aim is to find all the possible values of

the values of z.
Must always represent roots on a unity circle.
The roots form a regular polygon, and are conjugate pairs.

( xz )( xz )=x 22 ( z ) x +|z|

Locus

|z(a+ib)|=c

and consequently find all

Done geometrically.
Circle, centre (a, b), radius c.

z( a+ib)
=1
z( c+id)

Thompson Ly
4

Factorise over complex

field.

Done geometrically.
Perpendicular bisector of interval joining (a, b) and (c, d).

4 Unit Maths Complex Numbers

z( a+ib)
= k (where k 1)
z( c+id )

Done algebraically.
Change z into x + iy.

arg [ z( a+ib)] =

Done geometrically.
A ray coming from (a, b) Let equation of locus be y = mx + b.

(angle with respect to the positive x-axis).

arg

arg

Open circle at (a, b).

Restrictions do apply.

arg

Thompson Ly
5

z (a+ ib)
=0
z (c +id )
Done geometrically.
This is a part of a straight line which passes through (a, b) and (c, d).
Restrictions: cant be (a, b) or (c, d).

z (a+ ib)
=any other angle
z (c +id )
Draw diagram remember direction of angle.
Redraw diagram, where z is the perpendicular bisector of the interval made
from (a, b) and (c, d) so that it is easier to find the equation of the circle.
Draw triangles to work out radius and centre.
Restrictions: above or below the line passing through (a, b) and (c, d), not
including (a, b) and
(c, d).