Forensic Mathematics A detective discovers a murder victim in a hotel room at

9:00am one morning. The temperature of the body is 80.0 F. One hour later, at
10:00am, the body has cooled to 75.0 F. The room is kept at a constant
temperature of 70.0 F. Assume that the victim had a normal temperature of 98.6
F at the time of death. Use the differential equations to find the time the murder
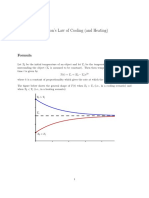
took place. Let u(t) be the temperature of the body after t hours. By Newtons Law
of Cooling we have the differential equation

du
=k (u70)
dt
where k is a constant (to be determined). Solve the differential equation and get a
formula for u(t).

Determination of time of death

Police arrive at the scene of a murder at 12 am. They immediately take and record
the body's temperature, which is 90o, and thoroughly inspect the area. By the time
they finish the inspection, it is 1:30 am. They again take the temperature of the
body, which has dropped to 87o, and have it sent to the morgue. The temperature at
the crime scene has remained steady at 82o. When was the person murdered?

Example 1: The Big Pot of Soup

As part of his summer job at a restaurant, Jim learned to cook up a big pot of soup
late at night, just before closing time, so that there would be plenty of soup to feed
customers the next day. He also found out that, while refrigeration was essential to
preserve the soup overnight, the soup was too hot to be put directly into the fridge
when it was ready. (The soup had just boiled at 100 degrees C, and the fridge was
not powerful enough to accommodate a big pot of soup if it was any warmer than
20 degrees C). Jim discovered that by cooling the pot in a sink full of cold water,
(kept running, so that its temperature was roughly constant at 5 degrees C) and
stirring occasionally, he could bring the temperature of the soup to 60 degrees C in
ten minutes. How long before closing time should the soup be ready so that Jim
could put it in the fridge and leave on time?