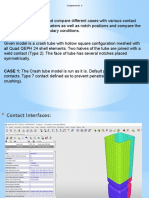
Describing problem for each

1. Static, non-linear analysis of a thin plate using large displacement because of the thin
element having large deformation. Also, use the thickness of 2mm to perform the analysis.
2. Static analysis to study the non-linearity with both large displacement and of no
penetration contact using solid element. Also, apply a contact set between the 2 surfaces
likely to interact.
3. Showing a large displacement non-linearity is important to use in our solution even when
the deformations are not large. Using 2nd configuration of the model and perform a static
study and doing both linear and non-linear consecutively.
Describe boundary conditions for each
1. Fixed BC on left-most edge.
2. Fixed restrained on the bottom of the bottom tip
3. Fixed BC on the outside edge of the object. Roller/slider fixture to represent the rest of the
plate.

Describe loads for each

1. Force on the inside edge of the hole. 10N downward (-y-direction).
2. 5N downward force, normal to the surface on the opposite side of the boundary condition.
3. 0.3 MPa pressure on the top.

Give material for each

1. Alloy steel.
2. Nylon 6/10.
3. Cast alloy steel.
Results plot for each
1.

Top and bottom shell element.

2.
3.
Comment and discuss results:
1. Von Mises stress for top element is 265 MPa, bottom is 282 MPa and the yield strength is
221 MPa -> Max von Mises stress is 282 MPa. The difference between top and bottom
stresses are due to large displacement non-linear analysis. Therefore, the edge on
opposite sides are not equal.
2. The von Mises stress is 56 MPa and the yield strength is 139 MPa
3. The displacement is about 8.6mm which is roughly twice the elements size. Non-linear
results are substantially smaller (5.32mm displacement). Large displacement is a required
assumption because membrane stress affects the stiffness of the model.