Infinite potential well

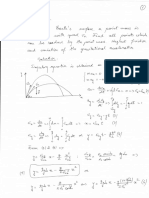
1) Determine the energy levels and the normalized wave functions of a particle in a potential well:
0, for 0 xa
V ( x) .
, for x 0 and x a
2) The statistics of the operators Q x , Q x2 , Px and Px2 using their coordinate representation.
3) Discussion on Heisenberg uncertainty relation as a function of n.
2
4) (facultative) Obtain and represent graphically the momentum probability distribution px n for
the particle in the n-th energy eigenstate. Here p x is the generalized eigenvector of the linear
momentum operator Px p x p x p x .

Solution:
Px2
1) Employ the notations H V ( x) in the operator language and then the coordinates
2m
2
d2
representation: H V ( x) . Solve H E ( x) E E ( x) .
2m dx 2
Step 1: Determine the analytical form of the wave function.
Step 2: Impose the continuity conditions. Determine the energy.
Step 3: Impose the normalization relation. Obtain the final form of the wave function.
n
The wave function inside the well should be: E ( x) n ( x) A sin x , with the normalization
a
2 22 2
constant A and the energy eigenstates En n .
a 2ma 2
Outside the well, the wave function should be zero.

2) Calculate:
a 2

Qx n Qx n x x n dx
0
2

a
2
Q n Q n x
2
x
2
x
2
x n dx (Qx )2 Qx2 Qx
0
a
d
Px n Px n n* ( x) n ( x ')dx '
0
i dx '
2
d

a 2 2
P n P n
x
2
x
2
n ( x ')
*
n (x ')dx ' (Px )2 Px2 Px
i dx '
2
0

3) Discuss (Qx )2 (Px )2 , as a function of n.