Professional Documents
Culture Documents
Optimum Thrust-Nozzle Contours For
Uploaded by
Baptiste RéaudCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Optimum Thrust-Nozzle Contours For
Uploaded by
Baptiste RéaudCopyright:
Available Formats
1886 AIAA JOURNAL VOL. 5, NO.
10
Technical Notes.
TECHNICAL NOTES are short manuscripts describing new developments or important results of a preliminary nature. These Notes cannot exceed 6 manuscript
pages and 3 figures; a page of text may be substituted for a figure and vice versa. After informal review by the editors, they may be published within a few months of
the date of receipt. Style requirements are the same as for regular contributions (see inside back cover).
Optimum Thrust-Nozzle Contours for p(uvx + vvy} + Py + App(v - vp) = 0 (3)
Gas-Particle Flows 2
uPx + vPy - a (upx + vpy) - ABpp = 0 (4)
JOE D. HOFFMAN* AND H. DOYLE THOMPSONf (ypPUp)x + (yppVp)y = 0 (5)
Pur due University, Lafayette, Ind.
PP[UP(UP)X + vp(up)v - A(u - up)] = 0 (6)
M ANY current high-energy propellant combinations use
metal additives that give rise to performance losses due
to the nonequilibrium effects of particle drag and heat trans-
Pp[up(vp)x + vp(vp)y - A(v - vp)] = 0
pp[up(hp)x + vp(hp)y + %AC(TP -T)] = Q
(7)
(8)
fer. Hoffman and Lorenc1 studied these losses in conical
Downloaded by MONASH UNIVERSITY on March 6, 2015 | http://arc.aiaa.org | DOI: 10.2514/3.4321
nozzles. Their results indicate that performance can be The parameters A, B, and C are drag and heat-transfer
improved by proper nozzle contouring. The present analysis parameters defined in Ref. 3.
presents an optimization technique for the design of axi- Equations (1-8) are for a single particle size of one chemi-
symmetric nozzles whose working fluid is a gas-particle mix- cal species. Generalization to more than one particle size
ture. The details of this analysis are presented in Ref. 2. and more than one species can be accomplished at the expense
The analysis is based on the usual assumptions for axi- of more complex algebra.
symmetric gas-particle flows as discussed in Ref. 3. The The model to be considered is illustrated in Fig. 1. The
optimization procedure applies to the supersonic portion of formulation of the optimization is similar to that presented
the nozzle. The flowfield up to the supersonic region and the by Guderley and Armitage.4 The right-running character-
initial expansion of the supersonic flowfield are assumed to istic ADB separates the flowfield into the upstream region
be known. The determination of the flowfield through the which is fixed by the given subsonic and transonic contour,
kernel (see Fig. 1) is discussed in Ref. 3. and into the downstream region which will be affected by
The differential equations governing the axisymmetric variations in the nozzle contour AC. The problem then be-
flow of a gas-particle mixture are3 comes the determination of the optimized nozzle contour
y = rj(x) which develops maximum thrust for the given sub-
(ypu)x + (ypv)y = 0
sonic and transonic contour subject to the restriction of shock-
p(uux vuy) + Px 4- App(u — Up) = 0 (2) free flow and a constraint on the allowable supersonic con-
tour. The optimum nozzle contour is obtained by applying
the techniques of the calculus of variations.
There are no particles present in region A DEC since the
Limiting particle limiting particle streamline separates from the nozzle wall
streamline in the throat region and is not permitted to intersect the
nozzle wall downstream of the throat, i.e., point E lies be-
Nozzle contour tween points B and C on the left characteristic EEC. Region
A DEC is described by the equations which govern the gas-
particle flow in region DBE if the particle density pp is zero.
The extremal problem is then formulated in terms of the
expression
Right running /*/*
Sonic line B characteristic
' - v)]dx JJ ABC (9)
i =l
where d,C2(x) and hi(x,y), (i = 1, . . . , 8), are Lagrange
multipliers; the operators Li,(i = 1, . . . , 8), denote Eqs.
Fig. 1 Model for gas-particle flow optimization analysis. (1-8); and rj' = drj/dx. In Eq. (9) the axial thrust which
is to be maximized is obtained by integrating the excess
pressure forces acting on the nozzle wall AC. The Lagrange
Presented as Paper 66-538 at the AIAA Second Propulsion multiplier Ci multiplies the function G(7),r)',P), the actual
Joint Specialist Conference, Colorado Springs, Colo., June form of which can be chosen to impose any of a variety of
13-17, 1966; submitted June 8, 1966; revision received May 8, constraints on the nozzle geometry such as fixed nozzle
1967. This work was sponsored jointly by Aerojet-General length, fixed nozzle surface area, etc. The Lagrange multi-
Corporation under Contracts PO 802353 and PO 802357 and plier C*(x) is used to introduce the restriction that the line
by NASA under Grant NsG 592. The authors wish to ac- AC along which the thrust is maximized is the nozzle wall and
knowledge the work of K. G. Guderley and J. V. Armitage, upon a gas streamline. Equation (9) is required to be stationary
which the present analysis is based. [11.23] for independent variations in the parameters u, v, P, p, up, vp,
* Associate Professor of Mechanical Engineering, Jet Pro-
pulsion Center. Member AIAA. hp, pp, rj(x), Xc, and Yc.
t Assistant Professor of Mechanical Engineering, Jet Pro- Following the formalisms of variational calculus as pre-
pulsion Center. Member AIAA. sented by Miele,5 the variation of Eq. 9 results in a set of
OCTOBER 1967 TECHNICAL NOTES 1887
Euler equations which must hold over the region ABC and a hiydx - hs(udy - vdx) = 0 (27)
set of transversality equations and corner conditions which
apply along the boundary ABC. These equations are pre- yhi - tfhi = 0 (28)
sented in Ref. 2. The Euler equations are a set of eight
quasilinear, nonhomogeneous, partial differential equations and on BE,
involving the gasdynamic properties and the Lagrange multi- h5 = hs = h7 = h* = 0 (29)
pliers hi. These equations, together with Eqs. (1-8), form
a hyperbolic system of 16 partial differential equations which On AC, the following two conditions are obtained:
can be replaced by the following equivalent system of char-
acteristic and compatibility equations. Along gas stream- uhz - vh2 = vy - u$G/dP)[r]r}'(P - P0)/G]xc (30)
lines dy/dx = v/u and
pudu + pvdv + dP = —App[(u — up)dx + X
pcu<
(v - vp)dy] (10) [ _ ^'(dfl/cV - Polype' r*c 1
(Pc -
X
udP - a*udp = ABppdx (11) L G(XC) G(XC) Jx rjpu
ypu
-h2du - hsdv - (ht/p)dP dv
pu dx
ydhi + udhz + vdh9 = Kidx + K2dy (12)
~
(h2v - h3u)dv + (hz/p)dP - (j - i)ua*(h*/p)dp + Equations (30-31) both contain the generalized design con-
Downloaded by MONASH UNIVERSITY on March 6, 2015 | http://arc.aiaa.org | DOI: 10.2514/3.4321
straint G (77,17;,P).
yudhi — ua2dh± = The particular geometric constraint is imposed by intro-
z
[-a h,v/y - a*Ks + K, - A(pp/p) X ducing the appropriate form of G into Eqs. (30-31). For
(hzdy/dx - h3)(v - vp)]dx (13) a fixed nozzle length G = 1 and for a fixed nozzle surface
area G = (I + ??' 2 ) 1/2 - It is apparent that other engineering
Along gas Mach lines dy/dx = tan(0 ± a) and constraints can be introduced in a similar manner.
A complete set of characteristic and compatibility equa-
az(vdu — udv) ± («2/p) cotadP = tions for the gasdynamic properties and the Lagrange multi-
(udy - vdx)(a2v/y) - A(pp/p)
X pliers has been obtained. The characteristics are the gas
and particle streamlines and the gas Mach lines. The
{B(udy — vdx) — a*[(u — up)dy — (v — vp)dx]} (14) compatibility equations for determining the gas properties
and their associated Lagrange multipliers are Eqs. (10-13
kudu + h3dv + (Vp) (dP - a*dp) - ydhi =F and 14-15), and those for determining the particle proper-
h^) = ± i^na(K^dx — Kidy) ± ties and their associated Lagrange multipliers are Eqs. (16-25).
— vdx){A(pp/p)\h%(u — up) + The design of an optimized nozzle contour requires an itera-
tive approach in which a likely contour is assumed initially.
h*(v - vp) - h*B] + Ki} (15) The boundary conditions, the flow variables, and the La-
grange multipliers are calculated for the assumed contour.
Along particle streamlines dy/dx = vp/up and In this calculation one of the boundary equations, Eq. (27),
updup = A(u — up)dx (16) is not required and becomes the check condition to deter-
mine if the assumed contour is the optimum contour. Thus,
Updvp = A(v — vp)dx (17) along BC, an error parameter E can be evaluated as
updhp = -IAC(TP - T)dx (18) = yhidx — hz(udy — vdx) (32)
d^p = 0 (19) If E is everywhere zero along BC, then the contour satisfies
all requirements of the variational problem and is indeed the
(iW* = yppUp (20) optimum contour. Otherwise, the contour must be altered
such that E goes to zero on BC.
(tp)y = -yppVp (21) Guderley and Armitage4 discuss a relaxation technique
which they have successfully applied to their problem. Re-
yupdhs = K8dx (22) cent unpublished work on a similar problem at Purdue
updh* = -K5dx (23) University indicates that a much simpler relaxation tech-
nique can be used since a change in the slope of the nozzle
vpdhi = hsdup + h7dvp + h^dhp + K&dy — ydh5 (24) contour propagates its effect primarily along the character-
istics of the flow.
updh8 = Kidx (25)
In Eqs. (14-15) the upper and lower signs refer to right- References
1
and left-running Mach lines, respectively. The particle Hoffman, J. D. and Lorenc, S. A., UA parametric study of
stream function \f/p is introduced to eliminate a deficiency gas-particle flows in conical nozzles," AIAA J. 3, 103-106 (1965).
2
in the compatibility equations which results from the original Hoffman, J. D. and Thompson, H. D., UA general method for
system of equations. This new system is in every way determining optimum thrust nozzle contours for gas-particle
equivalent to the original system. The terms KI through flows," AIAA Paper 66-538 (June 1966).
3
KS are defined in Ref. 2 and are nonhomogeneous terms in- Hoffman, J. D., "An analysis of the effects of gas-particle
mixtures on the performance of rocket nozzles/' Jet Propulsion
volving the gasdynamic properties and Lagrange multipliers, Center, Purdue Univ., TM-63-1 (January 1963).
but no derivatives. 4
Guderley, K. G. and Armitage, J. V., "General approach to
The transversality and corner conditions produce the optimum rocket nozzles," Theory of Optimum Aerodynamic
following boundary conditions for the Lagrange multipliers. Shapes, edited by A. Miele (Academic Press Inc., New York,
On BEC, 1965), Chap. 11.
5
Miele, A., Theory of Optimum Aerodynamic Shapes (Academic
hiydy + h2(udy — vdx) = 0 (26) Press Inc., New York, 1965), Chap. 4.
You might also like
- Difference Equations in Normed Spaces: Stability and OscillationsFrom EverandDifference Equations in Normed Spaces: Stability and OscillationsNo ratings yet
- 3876 7634 1 PBDocument19 pages3876 7634 1 PBItalo AdottiNo ratings yet
- A Course of Mathematics for Engineerings and Scientists: Volume 5From EverandA Course of Mathematics for Engineerings and Scientists: Volume 5No ratings yet
- On Noteworthy Applications of Laplace Transform in Real LifeDocument7 pagesOn Noteworthy Applications of Laplace Transform in Real LifeInternational Journal of Innovative Science and Research Technology100% (2)
- On Noteworthy Applications of LaplaceDocument7 pagesOn Noteworthy Applications of LaplaceInternational Journal of Innovative Science and Research TechnologyNo ratings yet
- Analysis of Transport Phenomena in A Two-Phase CO2 Supersonics EjectorDocument5 pagesAnalysis of Transport Phenomena in A Two-Phase CO2 Supersonics EjectorSanika TalathiNo ratings yet
- Numerical Simulation of Urban Ventilation With Different Building Scales MetDocument6 pagesNumerical Simulation of Urban Ventilation With Different Building Scales MetVincenzo PicozziNo ratings yet
- Cohomology Operations (AM-50), Volume 50: Lectures by N. E. Steenrod. (AM-50)From EverandCohomology Operations (AM-50), Volume 50: Lectures by N. E. Steenrod. (AM-50)No ratings yet
- Energies: Harmonic Spectrum of Output Voltage For Space Vector Pulse Width Modulated Ultra Sparse Matrix ConverterDocument13 pagesEnergies: Harmonic Spectrum of Output Voltage For Space Vector Pulse Width Modulated Ultra Sparse Matrix ConverterAndréNo ratings yet
- Technical Note Prepared by Beicip-Franlab/IFP Principles of Athos Dual Medium Reservoir SimulationDocument8 pagesTechnical Note Prepared by Beicip-Franlab/IFP Principles of Athos Dual Medium Reservoir SimulationGadhoumiWalidNo ratings yet
- Numerical and Experimental Simulation of An Axisymmetric Supersonic InletDocument6 pagesNumerical and Experimental Simulation of An Axisymmetric Supersonic InletalexNo ratings yet
- Optimal Power Flow Solution UsingDocument5 pagesOptimal Power Flow Solution UsingIJARTETNo ratings yet
- Dynamic Characteristics of Pneumatic Transmission Lines and Its Equivalent SystemsDocument11 pagesDynamic Characteristics of Pneumatic Transmission Lines and Its Equivalent Systemsbaja2014No ratings yet
- Two Nonlinear Models of A Transversely Vibrating StringDocument8 pagesTwo Nonlinear Models of A Transversely Vibrating StringGeorg BekesyNo ratings yet
- 4994 Load Flow Analysis by Gauss-Seidel PDFDocument8 pages4994 Load Flow Analysis by Gauss-Seidel PDFMartin AwaseNo ratings yet
- Super Imposed FlowsDocument4 pagesSuper Imposed FlowssuriyaanaNo ratings yet
- Read2016 OrbitalPropagationChebyschevDocument18 pagesRead2016 OrbitalPropagationChebyschevJORGE IVAN ZULUAGA CALLEJASNo ratings yet
- A New Continuous Contact Low-Noise Gear Pump: K. MitomeDocument6 pagesA New Continuous Contact Low-Noise Gear Pump: K. MitomeMorteza ShakerienNo ratings yet
- Rao Bone TCST 2007Document17 pagesRao Bone TCST 2007sangtk55No ratings yet
- Non DimensionalizationDocument3 pagesNon Dimensionalizationnlayton620No ratings yet
- A Novel P-Q Control Algorithm For Combin PDFDocument8 pagesA Novel P-Q Control Algorithm For Combin PDFvidya_sagar826No ratings yet
- Ec. de Martin PDFDocument17 pagesEc. de Martin PDFMaggyBalcazarNo ratings yet
- Quispel 2008 J. Phys. A Math. Theor. 41 045206Document8 pagesQuispel 2008 J. Phys. A Math. Theor. 41 045206Abid MullaNo ratings yet
- Spe 72361 MSDocument21 pagesSpe 72361 MSAbbas AlkhudafiNo ratings yet
- Optimum Power Flow Analysis by Newton Raphson Method, A Case StudyDocument9 pagesOptimum Power Flow Analysis by Newton Raphson Method, A Case StudyNurul Ain RosdiNo ratings yet
- On Combined Plant and Control Optimizati PDFDocument9 pagesOn Combined Plant and Control Optimizati PDFSouleyman RNo ratings yet
- Design of Maximum Thrust Plug NozzlesDocument7 pagesDesign of Maximum Thrust Plug NozzleskannarockNo ratings yet
- Analysis and Performance Assessment of Six-Pulse Inverter-Fed Three-Phase and Six-Phase Induction MachinesDocument9 pagesAnalysis and Performance Assessment of Six-Pulse Inverter-Fed Three-Phase and Six-Phase Induction MachinessouravghimireyNo ratings yet
- CSTR Energy Balance PDFDocument182 pagesCSTR Energy Balance PDFfasdasd123No ratings yet
- Slides Enbal PDFDocument139 pagesSlides Enbal PDFOmar GutierrezNo ratings yet
- Wang 2012Document5 pagesWang 2012Tarak BenslimaneNo ratings yet
- Chapter 14-OscillationsDocument23 pagesChapter 14-Oscillationszeus292122No ratings yet
- An Implicit Method For Transient GasDocument6 pagesAn Implicit Method For Transient GasJuanCarlos Arias SantanaNo ratings yet
- Implicit Finite-Difference Simulations of Three-Dimensional Compressible FlowDocument9 pagesImplicit Finite-Difference Simulations of Three-Dimensional Compressible FlowFah MatNo ratings yet
- De AssignmentDocument19 pagesDe AssignmentMuhammad UzairNo ratings yet
- MATHEMATICAL MODELLING OF WIND FARM AND HYBRID SOURCE POWER QUALITY IMPROVEMENT USING STATCOM Ijariie7635 PDFDocument8 pagesMATHEMATICAL MODELLING OF WIND FARM AND HYBRID SOURCE POWER QUALITY IMPROVEMENT USING STATCOM Ijariie7635 PDFLalitNo ratings yet
- Comparison Source Term Formulations For Hybrid CFD CAA Method EWERTDocument13 pagesComparison Source Term Formulations For Hybrid CFD CAA Method EWERTAbhishek PillaiNo ratings yet
- Bond Graph Interpretation of One-Dimensional Fluid FlowDocument13 pagesBond Graph Interpretation of One-Dimensional Fluid FlowMejbahul SarkerNo ratings yet
- A General Approach of Space and Time Harmonics Interactions in Induction MotorsDocument4 pagesA General Approach of Space and Time Harmonics Interactions in Induction MotorsYUDHAJIT ROYNo ratings yet
- Trajectory GenerationDocument6 pagesTrajectory GenerationHala El OuarrakNo ratings yet
- Riska DewiDocument2 pagesRiska DewiadelusiNo ratings yet
- Chapter 6 PDFDocument13 pagesChapter 6 PDFMarcosNo ratings yet
- 0.3 Imprimir10.1.1.735.9782Document12 pages0.3 Imprimir10.1.1.735.9782Alfonso López JiménezNo ratings yet
- Thrust Vector Control by Flexible Nozzle and Secondary Fluid InjectionDocument10 pagesThrust Vector Control by Flexible Nozzle and Secondary Fluid InjectionPurushothamanNo ratings yet
- Warping+Bernoulli Beam ModelDocument6 pagesWarping+Bernoulli Beam ModelTomás Bravo TetlakNo ratings yet
- Turbulence and Standing Waves in Oscillatory Chemical Reactions With Global CouplingDocument7 pagesTurbulence and Standing Waves in Oscillatory Chemical Reactions With Global CouplingVikram VenkatesanNo ratings yet
- Up To Date - CatenaryDocument17 pagesUp To Date - CatenaryGileno DiasNo ratings yet
- Single-Phase PQ Theory For Active Filters: December 2002Document5 pagesSingle-Phase PQ Theory For Active Filters: December 2002Snehal GajreNo ratings yet
- Applsci 09 04411Document16 pagesApplsci 09 04411burchandadiNo ratings yet
- A Numerical Study On Flow Through The Spiral Casing of A Hydraulic TurbineDocument14 pagesA Numerical Study On Flow Through The Spiral Casing of A Hydraulic Turbinenadir adelNo ratings yet
- An Alternative Approach To Exact Solutions of A Special Class of Navier-Stokes FlowsDocument9 pagesAn Alternative Approach To Exact Solutions of A Special Class of Navier-Stokes FlowsRoberticoZeaNo ratings yet
- Experimental Methods in Seismic Engineering Fall 2018 Homework Set #1Document3 pagesExperimental Methods in Seismic Engineering Fall 2018 Homework Set #1Gerald JahoNo ratings yet
- Zhang 2017 IOP Conf. Ser. Mater. Sci. Eng. 281 012057Document8 pagesZhang 2017 IOP Conf. Ser. Mater. Sci. Eng. 281 012057Os ZaidNo ratings yet
- CFD Modelling Approaches Against Single Wind Turbine Wake Measurements Using RANSDocument17 pagesCFD Modelling Approaches Against Single Wind Turbine Wake Measurements Using RANSTareq Abdussalam KhamllagNo ratings yet
- S-Generalized Mittag-Lef Er Function and Its Certain PropertiesDocument11 pagesS-Generalized Mittag-Lef Er Function and Its Certain PropertiesLaid MerabtiNo ratings yet
- Comparison Between Fluent and FDSDocument11 pagesComparison Between Fluent and FDSSuraj MulayNo ratings yet
- Propriété de La Vapeur PDFDocument5 pagesPropriété de La Vapeur PDFBaptiste RéaudNo ratings yet
- Steam Batch Thermal Processes in Unsteady State ConditionsDocument35 pagesSteam Batch Thermal Processes in Unsteady State ConditionsBaptiste RéaudNo ratings yet
- Prediction of The Dew PointDocument9 pagesPrediction of The Dew PointBaptiste RéaudNo ratings yet
- 2012 MIT KFUPM McGovern Ejector Efficiency PDFDocument12 pages2012 MIT KFUPM McGovern Ejector Efficiency PDFeldwin_dj7216No ratings yet
- Analysis of Isothermal Variable Area Flow: by I. Carl Romer, JR., B.S., M.S., and AH Bulent Cambel. B.S., M.S., PH.DDocument4 pagesAnalysis of Isothermal Variable Area Flow: by I. Carl Romer, JR., B.S., M.S., and AH Bulent Cambel. B.S., M.S., PH.DBaptiste RéaudNo ratings yet
- Waste Incineration EmissionsDocument14 pagesWaste Incineration EmissionsConstantin StanNo ratings yet
- Waste Incineration EmissionsDocument14 pagesWaste Incineration EmissionsConstantin StanNo ratings yet
- Diseño de Separadores GLCCDocument23 pagesDiseño de Separadores GLCCAlejandro JoseNo ratings yet
- End CorrosionDocument4 pagesEnd Corrosiondafteri11No ratings yet
- Waste Incineration EmissionsDocument14 pagesWaste Incineration EmissionsConstantin StanNo ratings yet
- Diseño de Separadores GLCCDocument23 pagesDiseño de Separadores GLCCAlejandro JoseNo ratings yet
- End CorrosionDocument4 pagesEnd Corrosiondafteri11No ratings yet
- End CorrosionDocument4 pagesEnd Corrosiondafteri11No ratings yet
- Drag of A Disk Rotating in A Viscous FluidDocument50 pagesDrag of A Disk Rotating in A Viscous FluidBaptiste RéaudNo ratings yet
- Stiffness MatrixDocument2 pagesStiffness MatrixicabullangueroNo ratings yet
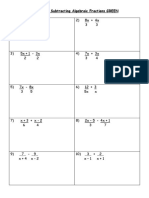
- Algebraic FractionDocument4 pagesAlgebraic FractionBaiquinda ElzulfaNo ratings yet
- Scan 1Document13 pagesScan 1MavisNo ratings yet
- Floor PlateDocument3 pagesFloor Platekeat_leong_yeeNo ratings yet
- Monetary Policy Problem Set #1 Long-Run Correlations. NotesDocument8 pagesMonetary Policy Problem Set #1 Long-Run Correlations. NotesYuliya KulikovaNo ratings yet
- Chapter 10 Solutions PDFDocument30 pagesChapter 10 Solutions PDFabcNo ratings yet
- Jordan Vneumann THMDocument3 pagesJordan Vneumann THMJamilu Adamu MusaNo ratings yet
- Fiitjee Class 5 Sample PaperDocument18 pagesFiitjee Class 5 Sample PaperPremta Kumari100% (1)
- Microecon Subject GuideDocument45 pagesMicroecon Subject GuideJoshua LamNo ratings yet
- Pragati Public School Class - Xi Annual Examination (2017-18) Sub:-Mathematics Set-A Time 3 Hrs. MM - 100Document3 pagesPragati Public School Class - Xi Annual Examination (2017-18) Sub:-Mathematics Set-A Time 3 Hrs. MM - 100Vansh GuptaNo ratings yet
- Fatigue Failure Theories:: Soderberg Line, Goodman Line and Gerber's ParabolaDocument5 pagesFatigue Failure Theories:: Soderberg Line, Goodman Line and Gerber's ParabolaHanan ShayiboNo ratings yet
- MODULE 2 Plane Geometry Quadrilaterals and PolygonsDocument9 pagesMODULE 2 Plane Geometry Quadrilaterals and PolygonsCyndelleNo ratings yet
- Class 8 - Portions & Time Table (Dec '21)Document1 pageClass 8 - Portions & Time Table (Dec '21)Midhun Bhuvanesh.B 7ANo ratings yet
- Small Engine SimulationDocument20 pagesSmall Engine SimulationAhmed SajitNo ratings yet
- A Bayesian Exploration of The Relationship BetweenDocument10 pagesA Bayesian Exploration of The Relationship BetweenErwin AntyNo ratings yet
- The Design of A Multi-Bit Sigma-Delta ADC Modulator: Yang Shaojun, Tong Ziquan, Jiang Yueming, Dou NaiyingDocument4 pagesThe Design of A Multi-Bit Sigma-Delta ADC Modulator: Yang Shaojun, Tong Ziquan, Jiang Yueming, Dou Naiyingchaitanya sNo ratings yet
- Silabus Manajemen StrategikDocument11 pagesSilabus Manajemen StrategikKarina AprilliaNo ratings yet
- StudentDocument15 pagesStudentVia AbadNo ratings yet
- 4.profit MaximizationDocument14 pages4.profit MaximizationRamyaNo ratings yet
- DSP SamplingDocument36 pagesDSP Samplingin_visible100% (1)
- GR 4 Unit 7 Part 1 Measuring Angles Form ADocument4 pagesGR 4 Unit 7 Part 1 Measuring Angles Form Aapi-280863641No ratings yet
- Important Ques WTH AnsDocument3 pagesImportant Ques WTH AnsLatta SakthyyNo ratings yet
- PaperpublishedDocument10 pagesPaperpublishedSamsam RaufNo ratings yet
- ThesisDocument8 pagesThesisdereckg_2No ratings yet
- Interpretar RegresionDocument5 pagesInterpretar Regresionpezamarillo-1No ratings yet
- Grafcet ECC95Document7 pagesGrafcet ECC95Valkure OmegaNo ratings yet
- Officer, General Admin, Level 6Document8 pagesOfficer, General Admin, Level 6Prashant GautamNo ratings yet
- Sparks of GeniusDocument23 pagesSparks of Geniusmaximus_2000No ratings yet
- CHP 3 Part OneDocument57 pagesCHP 3 Part OneMegha GuptaNo ratings yet
- Distributed Data Mining in Wireless Sensor Networks Using Naive Bayes ClassificationDocument10 pagesDistributed Data Mining in Wireless Sensor Networks Using Naive Bayes Classificationashish88bhardwaj_314No ratings yet
- Dark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseFrom EverandDark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseRating: 3.5 out of 5 stars3.5/5 (69)
- A Brief History of Time: From the Big Bang to Black HolesFrom EverandA Brief History of Time: From the Big Bang to Black HolesRating: 4 out of 5 stars4/5 (2193)
- Giza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyFrom EverandGiza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyNo ratings yet
- A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceFrom EverandA Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceRating: 4 out of 5 stars4/5 (51)
- Summary and Interpretation of Reality TransurfingFrom EverandSummary and Interpretation of Reality TransurfingRating: 5 out of 5 stars5/5 (5)
- The Beginning of Infinity: Explanations That Transform the WorldFrom EverandThe Beginning of Infinity: Explanations That Transform the WorldRating: 5 out of 5 stars5/5 (60)
- The Simulated Multiverse: An MIT Computer Scientist Explores Parallel Universes, The Simulation Hypothesis, Quantum Computing and the Mandela EffectFrom EverandThe Simulated Multiverse: An MIT Computer Scientist Explores Parallel Universes, The Simulation Hypothesis, Quantum Computing and the Mandela EffectRating: 4.5 out of 5 stars4.5/5 (20)
- Quantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessFrom EverandQuantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessRating: 4 out of 5 stars4/5 (6)
- Lost in Math: How Beauty Leads Physics AstrayFrom EverandLost in Math: How Beauty Leads Physics AstrayRating: 4.5 out of 5 stars4.5/5 (125)
- Knocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldFrom EverandKnocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldRating: 3.5 out of 5 stars3.5/5 (64)
- Midnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterFrom EverandMidnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterRating: 4.5 out of 5 stars4.5/5 (410)
- Packing for Mars: The Curious Science of Life in the VoidFrom EverandPacking for Mars: The Curious Science of Life in the VoidRating: 4 out of 5 stars4/5 (1395)
- Let There Be Light: Physics, Philosophy & the Dimensional Structure of ConsciousnessFrom EverandLet There Be Light: Physics, Philosophy & the Dimensional Structure of ConsciousnessRating: 4.5 out of 5 stars4.5/5 (57)
- Chasing Heisenberg: The Race for the Atom BombFrom EverandChasing Heisenberg: The Race for the Atom BombRating: 4.5 out of 5 stars4.5/5 (8)
- The Power of Eight: Harnessing the Miraculous Energies of a Small Group to Heal Others, Your Life, and the WorldFrom EverandThe Power of Eight: Harnessing the Miraculous Energies of a Small Group to Heal Others, Your Life, and the WorldRating: 4.5 out of 5 stars4.5/5 (54)
- Black Holes: The Key to Understanding the UniverseFrom EverandBlack Holes: The Key to Understanding the UniverseRating: 4.5 out of 5 stars4.5/5 (13)
- Beyond Weird: Why Everything You Thought You Knew about Quantum Physics Is DifferentFrom EverandBeyond Weird: Why Everything You Thought You Knew about Quantum Physics Is DifferentRating: 4 out of 5 stars4/5 (25)
- Quantum Physics: What Everyone Needs to KnowFrom EverandQuantum Physics: What Everyone Needs to KnowRating: 4.5 out of 5 stars4.5/5 (49)
- The Tao of Physics: An Exploration of the Parallels between Modern Physics and Eastern MysticismFrom EverandThe Tao of Physics: An Exploration of the Parallels between Modern Physics and Eastern MysticismRating: 4 out of 5 stars4/5 (500)
- The Holographic Universe: The Revolutionary Theory of RealityFrom EverandThe Holographic Universe: The Revolutionary Theory of RealityRating: 4.5 out of 5 stars4.5/5 (76)
- The Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeFrom EverandThe Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeRating: 4.5 out of 5 stars4.5/5 (3)
- The End of Everything: (Astrophysically Speaking)From EverandThe End of Everything: (Astrophysically Speaking)Rating: 4.5 out of 5 stars4.5/5 (157)