Solution Manual Chemical Engine PDF

Tnstructor’s Soltutions Introduction to CHEMICAL ENGINEERING THERMODYNAMICS Sixth Editson J.M. Smith ¢ H.C. Van Ness ¢ M.M. AbbottChapter 1 - Section A - Mathcad Solutions 1.4 The equation that relates deg F to deg C is: t(F ‘equation by setting t(F) = «(C). ‘Guess solution: Given Find(t) 240 5 a F 1.5. By definiti Peo F = massg 3000bar P-A 1.6 By definition: Pp = = F = massg 3000atm 1.7 Pabs = p-g:h + Patm 13,535.28 em? Patm = 101.78kPa 18 p= 13.535-50 om Pam !=29.86in_Hg Pats == p-8-h+ Patm 4 8 (C) + 32. Solve this Ans. Note: Pressures are in gauge pressure. A= 12.566mm" mass = 3844kg = Ans. A= 0.023 in? mass='10007 Ibm Ams. b= $6.38em Pabs = 176.808kPa Ans, f= 25.62in £27179 psia Ans. Pats1.10 Assume the following: p := 13.52% gi 98% om’, ea 400bar his 2 Ps h=302.3m. Ans. 1.11 The force on a spring is described by: F = K x where K is the spring constant, First calculate K based on the earth measurement then 2ytars based on spring measurement on Mars. On Earth: F = massg mass := 0.40kg, F c= massg F = 3.924N On Mars: 0.40em Fears °= Kx EMars = 1-453N FMars mass “Sears: Ans, BMars = 112 Given: 4 ps—pg and: p= MP a & Poenver Denver Separating variables and integrating: lope {*3) i P RT Pree ° After integrating: ‘Taking the exponential of both sides —Me Ap Benver and rearranging: latm Psea3 cov atm R = 82.06 Tes (10+273.19K ZDenver = Imi mol Me ne zpemver = 0.194 Rr Mey (tome) Ppenver >= Psca'e Ppeniee = 0.823atm Ans. denver = 0:834bar Ams. 1.13. The same proportionality applies as in Pb. 1.11. 2186-5 Almoon ?= 18.76 ¢ learth = Sloot Aleath = 113.498 Smoon M i= Alegrthlbm MS.113,498lbm Ans. Wimoon = M: moon B.767IbE = Ams. O0dolt T 114 cost = =20dollars jg Ltr costeleg = SGollars. 19 ht row 100k day Whe day 4 dollars costhuty = 18.262 Solas costelgg = 25.567 Solar yF yr goo dollars COSttotal *= COStbulb + COSteIee o “Ans. 11S Ds 125k mass == 250lbm gis 2.169% § Patm i= 30.12in_Hg A= 120787(2) F = PainrA + mase-g Ans. (b) Paps ae Paks + Ans. A (© Ale 17 Work = Fal APE := mass-g-Al 1.16 D:= 047m mass = 150kg Pot ‘= 101.57kPa Asp (a) F 2 Paige A + mass-g FS1900%10'N Ans. F 2 ()Pabs == Paps = 110! Ans, © Al:=0.83m Work := F-Al Work = 15,8481) Ans. AEp := mass-g-Al D2k7 Ans. 1.18, mass := 1250kg Eg six 10s Ans. Wotk =F 10°kJ Ans. 119 Weot = M2S-8-Ah 9 91.9.9 time Wdot 00W Wdot dot = ———> g-Ah-0.91-0.92Chapter 2 - Section A - Mathcad Solutions 24 (@) | Myp= 35-kg ze Sem Work := My-g-Az Work:= 1715} Ans. (b) AU total = Work AUsoigh = LTISKI Ans. (©) By Eqs. (2.14) and (2.21): dU + d(PV) = Cp-dT Since P is constant, this can be written: Miz0-Cp-d? = Myo-dU + Mypo:P-dV Take Cp and V constant and integrate: My2o-Cp-(t2~ t1) = AU total 25-kg O-deg’ AUrotal ~— ty = 20,02degC Ans. Miz0-Cp (d) For the restoration process, the change in internal energy is equal but of opposite sign to that of the initial process. Thus S1715k) Ans. Q = AU otal Q © In all cases the total internal energy change of the universe is zero. 2.2. Similar to Pb, 2.1 with mass of water = 30 kg. Answers ar @) W=3.43 kt (b) Internal energy change of the water = 2.86 kJ (©) Final temp. = 20.027 deg C (@) Q=-2.86 kd 52.4 The electric power supplied to the motor must equal the work done by the motor plus the heat generated by the motor. 9.7amp E:= ov Wdotmech = 1-25hp Weotelect = hE Wetecg = 1.067 10° W Qdot := Wdotelect ~ Wdotimoch Qdot £134.875W Ans. 2.5 Eq. (2.3): AU'= Q+W Step 1t02: AUty := -200) Wyo := -60003 Qi2 == AUY—Wi2 Qi $8109 Ans, Step 3 t0 4: Ans. Step 1 to 2 to 3 to 4 to 1: Since AU' isa state function, AU' for a series of steps that leads back to the initial state must be zero. Therefore, the sum of the AU' values for all of the steps must sum to zero. AUtyy = 4700) AUty3 = ~AUty2 - AUEsy- ALLY, AUg; = 40007 Ans. Step2to3: AUtp3=-4% 10°F Qo3 = -38003 Ans. Wo3 = AUQ3- Qos Wha = 5200" For a series of steps, the total work done is the sum of the work done for each step.Wat := W134i - Wi2 — W23 ~ W34. Step 4 tot: AUty == 47001 Qat = AUtg) - War Ans, Note: Qu23a1 = -Wi2341 241 The enthalpy change of the water = work done. M := 20:kg q 4.18 id ‘At := 10-degC ‘ ee eg dest M-Cp-At eS Ans, Wdot 2.12 Qs 75k —12KI W:= AU-Q i J Ans, AU ss -12-40 Q= AU Ans, 2.13. Subscripts: e, casting; w, water; t, tank. Then me AUy + My-AUy + mrAU, = 0 Let C represent specific heat, C= Cpecy Then by Eq. (2.18) meCerAty + My-Cw Aty + meCr At kg my = 40k my = Skg 50: ia Cte 05 te = 500-degC ty = 25-degC ty :=30degC (guess) Given =meCer(t2- te) = (my-Cw + meC)-(t2- tr) to = Find(t) wy SR7TeaeBe Ans. 7215 @ ) © 247 2.18 (a) (b) mass-g AE := AUt Azi= 50m Di=2m mdot := p-wA Wdot := mdot-g-Az. Wdot. =: ur = 7620-8 kg. Hy Ur +P Uo = 27844 kg Hg = Ug + P2-V2 ‘Aus 0022.44 ee cy = 4 AUt = mass-Cy-AT gk AEp := AUt AULA 4 180 Ans. 291433" Ans, 3 > 3 Az "Dp? A=3.42m 4 mndot = 1.571 x 10882 3 L697 1OKW Aus. Py = 1002.7-kPa Vy ene Hy #76313 b—— Ans. Tae a Po = 1500-kPa V2 = 169.7. gm AU :2 U2- Uj AH = HQ-Hy Ans, OH 2275.3 Ans.222 Di Sem. uy m 5 Dz = Sem (a) Foran incompressible fluid, mdot = constant = u,A4p = uyA,9. stant, By a mass balance, (b) 2.23 Energy balance: mdots-H3 — (mdoty-H + mdotz-H2) = Qdot Mass balance: mdot3 — mdot; ~ mdotz = 0 Therefore: mdoty-(H3 ~ Hr) + mdoty-(H3 - Ha) = Qdot or mdot-Cp-(T3 - T1) + mdoty-Cp-(T3 ~ T2) = Qdot T3Cp-(mdoty + mdotg) = Qdot + mdoty-Cp:Ty + mdoty-Cp-T2 Sdeg® —mdoty = 0.882 Ty = 75degC s 1g kg-K Qdot + mdot;-Cp-T; + mdotz-Cp-T2 ‘ty WWD238degC Ans. fmdoty + mdot)Cp a 43.295 deEC 2 2.25 By Eq. (2.32): AH+ x By contim eu incompressibility eieinltaSDp = 3.8m AT S.0.019degC Ans. ATE 0023degC Ans. 226 Ty = 300K T2:= 520K w= 10 5 Wsdot = 98.8kW —ndot = soit AH := Cp(T,-T1) AH = 6.402 109 Kemal By Bq. 2.30): a ye) Qdot = | AH + oe +) no ndot - Wsdot Qdot =+9.904kW Ans. 2.27 By Eq. (2.32b): also By continunity, ee eee uy = up constant area T Pe atts cpar = LR(t—1) 10Given ZR (T-T)) T2 *= Find(T2) ‘Ty = 578-821 rankine Ans, (119.15-degF) KI up = 200-2 Hy = 3492 Hb = mse 8 B es 2.28 uy aaa uy? — uy By Eq. (2.32a: Q:= Ha-Hi + Ans. Hyp 31125- kg (guess) By Eq. (2.32a): Given Ho =Hy ug := Find(uy) uyes7R36% Ans. Sg 3 3 Vy = 388.61 om ap V2 Continuity: D2 := Dy wv " Ans.230(a) ty = 30-degC ty = 250-degC -mol J Cv i 208 By Eq. (2.19): Q:= n-Cy-(t2-t) Q=13738kI Ans. ‘Take into account the heat capacity of the vessel; then 100-kg, cy = 05+ i. kg-degc (my-cy + n-Cy)-(2- 11) Q= 1101410 Ans. © 00-dege ty = 40edegC n= 4emol Cp = 29.1 _ mol-degC By Eq. (2.23): Q:= mCp-(.-ty) 18.62k] Ans, 231 (a) t = 70-deg? tz = 350-degF 3-mol BIU es 5 By Eq. (2.19): V = Se deg? by Eq. (2.19): Qe nCy(t2-ty) Q=4200BTU Ans. Take account of the heat eapacity of the vessel: BTU ay == 200+ Ib = 0.12-———— ey ~ Bardeu? Qs (myey +n-Cy)-(t2-11) O920BTU Ans. (b) ty = 400-degF tz = 150-degF = 4-mol BIU Cp = By Eq. (2.23): aan ty Bq. (2.23): Qs Cp(ty -t1) Ans.2.33 Hy = 1322.6—— Ha == 1148, oe up ot Tb Tbs s a 8° Vy = 3.058-—— Vo= 7814 y= Bin Dy 10in ibm Ib En? yor 4 Ib rade a ndot = 3.463 « 10° M u2= n997 see 22 =u Fg, (2.328): Wy := Hp-H) +2 W, = -173.99 BTU 2 Ib Wot :=-Wemdot Wat 2:39.52 hp Ans. BTU BTU ft gm 234 Hp 3075 — Hy = 330 2520-5 — molwe:= 4482 : ae ge eee mmol a 3 f f Vp 9255. Vy = 0.28 Dps4in Dz Tein 1 pe 7 nin Da dot = 679.2632 br We = 5360. BEY ibmol Ws Q = 98.9 BU mohwt Ibm 5g ATU Qdot := mdor-Q —Qdol, = =67128——= Ans. 132.37 kg. bar n = 34.602mol 28.9.2 mol Vy = 24942 ‘mol Whence —nP-2V4 Ans. V2 Given: Tee Tye = Tr3 Whence Tp := 3-Ty 1 Cp = 29-ioule AMs=Cp(T2-T1) A= I Ans. molK PoP Q:=0AH QS 602,081) Ans. QeW AU ss n Work exactly like Ex. 2.10: 2 steps, (a) & (b). A value is required for PV/T, namely R. J Ty = 293.15-K 333.15-K molK P} = 1000-kPa Pp = 100-kPa R 8.314 (a) Cool at const VI to P2 (b) Heat at const P2 to T2 cy=2R fe Tasty Ta = 29315K ATp:=T2-Tag ATp = 303.835K AT,:=Ty-Ty AT, = -263.835K 14AH, = Cp-ATp, AH = 8.841 10° mol : aed AU, = Cy-AT, AU, = 5.484 10° — mol 3m RT) Vi = 2437x109 Vp vp = 0.028 mol Pp ‘mol AUg+Vi-(P2—P1) Hy = -7.677% 10° f 5 oat mol AH ~ P2(V2- Vi) Uy = 6.315% 10° mol Ans. 183 34 35 Chapter 3 - Section A - Mathcad Solutions ifa_) petite) pM) p At constant T, the 2nd equation can be written: eae ml 22] = xaP 44.1810 bar! pz = 1.01-p P Pi na ‘ AP = 225.2bar Py 3 226.2bar Ans. em bi=2700-bar =e := 0.125- Pys= Lbar Pp = 500-bar em V2 Since Work = -| PdV a bit of algebra leads to P2 Work:=e] ——ap P=b P, Alternatively, formal integration leads to (ren sf KeatbP a: 3.910 %atm | 0.1107 ?-atm? 3000-atm Vi Left? (assume const.) Combine Eqs. (1.3) and (3.3) for const, T: P2 : Work = vf (a+ bP) PaP Work =1665aim-° Ans. Py 16Mis S-kg 3 Lom yea P= Lebar t= O-degC ty = 20-dege 1°" 1550 ke acide i 7 With beta independent of T and with P=constant, i iy iz B-dT Vo i= Vi-exp|B-(t2-t1)] AV = V2-V) AVotal = MAY AV poral = 7.638% 107 ‘Ans, Work :=-P-AVyoigt (Const. P) Ans. Q:= MCp-(t2- ty) Ans. Agta °= Q Ans. AUjotal = Q+ Work Ans. 2 38 pi Bbar Pps bar = T= 600K Cp c= ZR (a) Constant V: WHO and SUS Q=Cy.AT AT:=1)-T, AT = -525K AU = Cy-AT Qand av sio91 ns. ano i ai AH := Cp-AT ‘AH = =15.28—— Ans. er (b) Constant T: AU = AH=0 and Q=Ww P2) Bias eg Work := R-Ty-in| 22 | Q and Werk 2103722 ans Pi) ‘mol (©) Adiabatic: Q=0 and AUS WCyAT 7and Step 41: Adiabatic P2 = 3bar T Step 12: Isothermal 12 {2 PL) War: 00K AU wt 18 : AH = Cp-AT a= -792t5 Ans ‘mol 3 3m Vp = 4.988% 107 mol Tq = 378.831K Aug) = 4597 10 mol AHgy = 6.436 1082. mol f Qs) = 0— mol War = 4.597% 10° mol 3 Vo = 0.01720 mol aU, = 0J mol AK » AH = Pe 3 J Qi -R-TrInj =| Qi = 6.006% 10° — Pi mol 6.006 10° mol Wiz -Qi2 Wi2= P3-V: X03 15 = 400K P3:=2bar V3 = V2 Ts R Cy(T}-T2) AUg3 = 4.157% 103 Step 23: Isochoric U3 mol Allg = Cp(T3—T2) AHg3 = ~5.82x 10° mol J Qx3 = Cy(T3-T) — Qx3 = 4.157 10° — mol Was = 0 Wo = 0-4 mol mol 3 P4 = 2bar T4 = 378.831K V4 = 0.016 mol ‘Step 34: Isobaric AU3g = Cv(T4- 13) AU34 = 439. on mol J Cp(T4-T3) AH3g = -615.996— mol Qs4 = 615.996 mol W54 = 175.9994, mol 3.10 For all parts of this problem: T2=T, and AUS AH=0 Also Q = -Work and all that remains is to calculate Work, Symbol V is used for total volume in this problem, 192m Vo i= em! P2) Pp) @ Work = a-R-T-In] = Work := P)-Vj-In] Pi Pi) Work = 2982k Ans. (b) Step 1: adiabatic compression to Py (intermediate V)__Vj = 2.702m° Wy = 3063kI a Step 2: cool at const P, to V2 Wo = -P2-(V2- Vi) W = 2042kJ Work := Wy + W2 Woik= $105k7 Ans. (©) Step 1: adiabatic compression to V, fy,yt Pi =P} | (intermediate P) —_P; = 62.898 bar (V2, Wy = 7635k Step 2: No work. Work = 7635ki Ans. (a) Step 1: heat at const V, to P, Step 2: cool at const Py to V2 ~P2(V2-Vvi) W: }3200k) Ans. 20(©) Step 1: cool at const P, to V2 Wy = -P1-(V2- Vi) W, = 1100k3 Step 2: heat at const V; to P; W220 Work := Wy ‘Wor itdoia A" 3.17 (a) No work is done; no heat is transferred. AU'S AT=O T= Ty = 100-degC —_Not reversible (b) The gas is returned to its initial state by isothermal compression. (Vv Work = n-R-Tn 2) but MRT = Po-V> ae Vian? Vo Work := P2:V>_In Work = 878:9K1 Ans. re sis 3.18 (a) Py := 100-kPa Pp = 500-kPa Ty = 303.15-K 5 Cp cy=2 ves bead Adiabatic compression from point 1 to point 2: KE Qin = 0 AU,2 = Wi2 = Cv-aTi2 mol AU,2 = Cy{T2-T1) AH)2 = Cp(T2-Ti) Wig AU)2 ak AHy2 = 5.13 eT Same) 24Cool at P, from point 2 to point 3: = AHD3 AHQ3 Ans. kK Qag = 5.15 Ans. mol Isothermal expansion from point 3 to point 1: AU) = AH) = 0 FORTHE CYCLE: AU = AH = 0 Q= Qin + Q3+Q51 Work := Wy2 + W23 + W3i Qaa oo Work vo04 2 SSS Snel 5 ‘mol (b) [each step that is 80% efficient accomplishes the same change of state, all property values are unchanged, and the delta H and delta U values are the same as in part (a). However, the Q and W values change, 2 Step 12: Wiz = — P 12 08 Qu2 = AU 2 ~ Wir Ww: Step 23: Wo3 52 0.8 2Qg3 == AUp3 ~ Wo3 Step 31: W3) = W31-08 Qs = -W31 FOR THE CYCLE: Q = Qi2+Qz3+Q31 pene 192 — mol 3.19 Here, V represents total volume, vi (a) Isothermal: y= Ppt V2 eT z= 600K P= 200kPa = Ans. v es Work = PV; ma ‘SOR) Ans. Wa vi Po V2 b) Adiabatic: Pep tee Tye? (0) Adiabati: 2 @) eT BY P25 69.65kPa Ans. 994.4k) Ans, 23(c) Restrained adiabatic: Work = AU = Pex AV 100-kPa Work = ~Pexr(V2- Vi) Work'=400KI Ans. Pext PrVi AU = neCy-AT. T2SARTIK Ams P2= 147:57KPa Ams. 3.20 ‘T3 := 323.15-K Step 12: R-Tyln@) Qi Wi 2.50244 mol KI a AUp3 == Cy-(T3 -T2) Q23 == AU23 Als ki Qa3 = -2.079— AU23 = 2.070 mol mol Process: Work := W)2 + Wo3 Qi Qi2t G3 Age 24AH == AH}2+AFy3 AU = AU 2 + AUa3 321 By Rq. 2.328), unitemass basis: motwt = 28-2 ane Lau? =o mmol 2 But AH = Cp-AT Whence AT = 322 3 = 403.15-K AU = 20792 Ans, mol Each part consists of two steps, 12 & 23. Work := W23 wok 67608. Ans. = = mob 2Q:= AU — Work Qe e463 Ans. = mol Tre Ts AU)? = Cy(t2-T) cp(t2-N) Qu2 = AH ky 2 = -Q12 W)2 = -0.831— Wi2 = AU}2- Qua 12 sy P3 kJ W 3 := R-To-Inj — W323 = 7.718 — 93 := RT (2) 23 Ral Work := Wi2+ Was Work = 6.986 Ans. EE pene es eA i Q = AU - Work Q=-4808— = Ans. Pinal os © bet P= P3 Ty (2) Pi AHp3 = Cp-(T3-T2) 03 := AH3 AUp3 = Cy-(T3 - Ta) Work := Wi2 + W23 Woks Ans. ‘mol Q = AU - Work Q=-2.894 For the second set of heat-eapacity values, answers are (kJ/mol): AU = 1.247 AU = 2.079 (a) Work = 6.762 Qe 26 51S3.23 3.24 (b) Work = 6.886 = Q= ~5.639 © Work = 4.972 Q= -3.725 Ty = 303.15-K Toi=Th T3 = 393.15-K Py = I-bar P3 := 12-bar Forthe process: AU:= Cy(T3-T)) AH = Cp(T3-T1) av= isnt mol Step 12: P AS a cep 12: Pa i= Pye eect KI Wi2 = 5,608-— mol Step 23: For the process: Q= Qin+ Qs Ans. Work = W3 = -P2(V3~ V2) = -R.(T3 -T2) But T3=T) So. Work = R-(T2-T;) >) Also WERT) “(| ‘Therefore 1 (p\ 12-T In} ae sf 50-K Py = 4-bar PB) OT 27328 3.26 ™2-T aa P Pre == | PS227obe Ans. 1 Va t= 256-em> Define: ae Py Assume ideal gas; let V represent total volume: P)-Vp= P2(Va+Vp) From this one finds: ap__-Va VatteD 4 Vp Vp 37503cm? Ams. Py Vat+VB r T)=300K Pj Cy =Cp-R ‘The process occurring in section B is a reversible, adiabatic compression. Let P(fina) = P2 Ta(final) = T Tp(final) = Ty nA = ng, Since the total volume is constant, 2naRT1 _ nyR(TA+Tp) u = = o (a) Pp := 1.28-atm Q) Pr Ta c= 2-Ty Ae Q=na(AUa + Ug) Define = 2 q=Cy(Ta+Ta-271) A Ta = 43025K Ans,(b) © @ Combine Eqs. (1) & (2) to eliminate the ratio of pressures: Ta 23 425-K (guess) Tp = 300-K Given Ans. TatTh Poss P| qa Ans. 21 cy(Ta+Ta-2T71) Ans. Tp = 325K By Fa. 2), fe) Pp = Py (2) Pee 182Fatm Ans. 1 Tas 2Tpo-Ty @ Ans. ar 2T rT = Cy(Ta+Tp- 2-4) Ans. Eliminate Ty +Tp from Eqs. (1) & @): P, = ip Ans. 2TCy Q) Ti =319.06K Ans. a Ans.373.15-K bax? Guess: yet Given Guess: vo:e RT P2 Given ie < V2:=Find(V2) V2 Va v2 Eliminate P from Eq, (1.3) by the virial equation: “ar Bc 1 [eS geeeas fork = 12.62 MseNe/ ° mmol ML (b) Eliminate dV from Eq. (1.3) by the virial equation in P: fel) Poy ave RT) = +C ar W:=-RT ere | a Cs a 30 3 Vi i= Find(Vi) Vy, = 30780" mol mol Ans.Note: The answers to (a) & (b) differ because the relations between the two sets of parameters are exact only for infinite series. 332 Te = 282.3K THDBISK Tye Ty = 1.056 Pe P, = 0.238 Pe (guess) 3 va ®t v= 2066S mol Given PVC RT “agem V := Find(V) v= 1919 Zz Ans. thol (b) By := 0.083 - oe Bo = 0.304 * By = 039-217 By = 2.262% 10> 742 Pr ee Z=1+(Bo +o: Bie £20932 (©) For Redlich/Kwong EOS: 0 Qe 0.08664 Table 3.1 Table 3.1 a(T,) = Eq. 3.51) ET2-P, B(Tr.P,) = a r Eq. (3.50) Calculate Z Guess: Given Eq. 3.49) Z-B(T,.Pr) + Blt e) a0) PP) ESE, Ri (ererBl PD) gery Find(Z) Z = 0.928 v ee 9165 Ans. (@_ For SRK EOS: e=0 2 = 0.08664 ¥ = 0.42748 Table 3.1 r ne | 2 ( 3] ‘Table 3.1 (Tyo) =[1 + (0.480 + 1.5740 - 0.17607) UT) ¥-0(Tr0) : a(t) eal) Eq.@51) — B(Tr,Ps) Eq. (3.50) Calculate Z Guess: 09 Given Eq. (3.49) Z= 1+B(Te,P,) —a(Tr)-B(tr Ps) ETN aR Zi=Find(Z) Z = 0.928 a Ans. (©) For Peng/Robinson EOS: wi o 1-¥2 Q:=007779 = 045724 Table 3.1 iN a(Tr,o) [ 1+ (037464 + 1.542260 - 0.269020") ( 11,7) Table 3.1 2Eq. (351) 8(T,.P; 2 or Eq. (3.50) or 4. Bs a(t. eee 4. (3.50) Calculate Z Guess: Given Eq. 3.49) Z= 1+B(Tr,Py) ~a(T,)-B(Tr,Ps) Ges Zi=Find(Z) Z= 0.92 333 Ty 3053K 9 -T=32ISK Tye z Tp = 1.058 oe = 4B. T2bar P= 1Scbar Pae P, = 0.308 Pe © = 0.100 vei mol Z=0907' Ans. Bo = -0.302 333 ERT y= e142 ans. fi EES OL P, 1+ (Bo +B) Za0ai? Vv (©) For Redlich/Kwong EOS: Q = 0.08664 WY = 0.42748 Table 3.1 Wa(T,) Table 3.1 (ts) = walt) Eq. @.51) QT Eq. 3.50) Caleulate Z Guess: 2-09 Given Eq. (3.49) 2Z-B(Tr.Ps) Z= 1+ B(TrPe) alt) BOP B(r.P))(Z + o-B(T.Ps)) Zi=Fink@) Z y= ZRT P (@)_ For SRK EOS: o=l 5:0 2 = 008664 = YY = 0.42748 Table 3.1 f yp Table 3.1 3 able 31 o):=|1 + (0.4804 1.5740 - 0.1760)-(1— 1,2 ¥-0(T,.0) ap, a(t) elte2) Eq.@51) — (T;,Py) 7 Eq. (3.50) Caleulate Z Guess 250.9 Given Eq. (3.49) zeal +8(T.P) a(t) BCC) Ea ee reptinP)) a Bia) 4Les ind(Z) Z = 0.907 Ve (©) For Peng/Robinson EOS: 142 o 1=$2 Q:=0.07779 = Y= 0.45724 Table 3.1 2 1 a(Tr.a) = [ + (0.37464 + 1.542260 - ol - Jl oa q(t) = ¥a(T.0) Bs) B(T,,P)) = ae Eq. (3.50) OT : Tr Calculate Z Guess: Z=09 Given Eq. (3.49) Z~B(Tr.Pr) Z= 1+B(Tr.P,) —4(T;)-B(Tr.Pal Find(Z) Z = 0.896 334 Te = 318.7K T= 348.15-K T, = 1.092 1S-bar =— Pr = 0,399 Pe (guess) 3 vekT ye i939 mol Given 35V = Find(V) 0.422 () Bo == 0.083 - == + 0.172 By = 0.139- > Tr Pr Zi=1+(Bp+o-By 7 Z= 0893 Ans. Bo = -0.283 By = 0.02 20,899. (©) For Redlich/Kwong EOS: o W = 0.42748 Table 3.1 w-a(T,) ‘ oe Eq. (3.51) a(Tr) q(T) am 4. B(T;,P,) = Eq. (3.50) Calculate Z Guess: 0.9 Given Bq. (3.49) Z= 1+B(Tr.Ps)-a(Tr) BrP) Z = Find(Z) (a) For SRK EOS: 1 Z = 0.888 2 := 0.08664 =P = 0.42748 Table 3.1 36Table 3.1 of ae W-a(T;,@) OT; a(t Eq. (3.51) B(tr,P,) Eq. (3.50) Calculate Z Guess: Z=09 Given Eq. (3.49) 2 148) a0) C8 ae Z=Find(Z) Z = 0.895 (©) For Peng/Robinson EOS: ozity2¢ -¥2 007779 -W = 0.45724 Table 3.1 a(Tr,@) = [ 1+ (0.37464 + 1.542260 ~ 0 ct ata v-a(Tro T,) » ~~ Eq. (3.51 TrP, eC) Saat 4-51) B(Tr.P, Eq. (3.50) Calculate Z Guess: Zi=09 Given Eq. 3.49) Z= 1+B(Tr.P.) ~a(T,)-B (TPs) Ea Ea Find(Z) ZRT P 0.882 v 37335 T= $23.15K 1800-kPa, Tr = 0.808 Py = 0.082 By = -0.281 Z= 0.939 (©) Table F.2: molwt := 18,0155 mol or 337 Z=0931 Ans. = 124.99-.molwt gm . HS ea Y= 22525 Ans. eS nol cm? D=5000-— — n:= mol mol?Ts 273.15-K Given ae lte tse £(P,V) = [ 4 1 0858 O86 2906 a@86 0858 [oes Pi=[- a0) bar oars] asia aaa 720) o782 0765 0822 140) 0.757) 0718 0.5+0.1781 10 O74 aati 05-0281) 180] O78 624 D503 ~_ 200) 0735 losr7 | 050.4161] O74 388 0540 468i Note that values of Z from Eq, (3.38) are not physically meaningful for pressures above 100 bar. 39BP; Zij= 1+ Eq. (3.37) 23; 0 7 Be Ze 2 = 20 7 7 1 40 0583] 0858 O86 60 0.306] 0.506; 0885 89 D867 0.888) 088 yoo] bar foar9| 0812 0749 120 0764 id oa 140 O7er a 050178 160) ‘O74 O87 05+028i1 120) 0733 0628 O5+O.366i 200 0735) 577 DE+OaT6I ‘o743| oss 0590. 468) Note that values of Z from Eq, (3.38) are not physically meaningful for pressures above 100 bar. 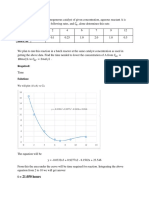Eq. 8.38)09 ZG 08 06 30 100 150 200 Pj-bar 2 3.38 (a) Propane: 169.8-K 42.48bar = 0.152 T := 313.15-K 13.71-bar T, = 0.847 Pris 2 P, = 0.323 c o & Q := 0.08664 = 0.42748 Table 3.1 w-a(T,) Table 3.1 kg. @. oT, Eq. (3.50) Caleulate Z for liquid by Eq. (3.53) Guess: Z:= 001 40Given Z= B(T;,Pr) +(Z + 6-B(Tr.P,)}-(Z +0: atta any ZRT cin Zs= Find(Z) Z = 0.057 veo O81 Ans. P <2 anol Calculate Z for vapor by Eq. (3.49) Guess: Given Tr ,Pr] 22 19 Blta) at OCP) eee ZRT 55 em Z:=Find(Z) — Z = 0.789 var Ne 092 Ans, Rackett equation for saturated liquid: T, Ans. For saturated vapor, use Pitzer correlation: 0.422 #0 Os Gore: Bg = -0.468 Ty 0.172 Bl eee By = -0.207 ve Verse Ans. atParts (b) through (t) are worked exactly the same way. All results are summarized as follows. Volume units are cu.cm./mote. RIK, Lig, R/K, Vap. Rackett Pitzer (a) 108.1 1499.2 94.2 1537.8 (b) 14.5 1174.7 981 1228.7 (©) 122.7 920.3 102.8 990.4 (@) 133.6 717.0 109.0 808.0 (@) 148.9 1516.2 125.4 1877.0 (1583 1216.1 130.7 1296.8 (g) 1704 971.1 1374 1074.0 (a) 1871 768.8 146.4 896.0 (i) 153.2 1330.3. 133.9 1405.7 @ 1642 1087.9 1403 11543 (kK) 179.1 835.3 148.6 958.4 @ 2014 645.8 160.6 795.8 (m) 61.7 12525 535 12769 (n) 64.1 1006.9 55.1 1038.5 (0) 66.9 814.5 57.0 853.4 (p) 703 661.2 59.1 707.8 (@ 644 1318.7 54.6 1319.0 (r) 674 1046.6 56.3 1057.2 (8) 70.8 835.6 58.3 856.4 (t) 748 669.5 60.6 700.5 423.39 (a) Propane Ty = 369.8 Po = 42.48-bar T = 313,15K P, = 0.323 o-l & Q. := 0.08664 WY = 0.42748 ’) a(t.) [| 1-+(0.480 + 1.5740 ~ 0.1760 W-a(Tr.0) i OP, a a(T;) == ¥-a(tro) Eq. (3.51) B(Ty,Pr) = Eq. (3.50) OT; Calculate Z for liquid by Eq. (3.53) Guess: Z=001 Given Z= p(ty,P,) +(2+68(te.P.)}{2 +08 (Tr.P9) aha (Ts) B(Te-Pr) ) Z=Find(Z) = Z= 0.085 -V sS Ans. Calculate Z for vapor by Eq. (3.49) Guess: Z=09 Given Z-B(TrP,) Z= 1+B(T:.Ps) —a(T): 8(1P) eat Zs eT) ind(Z) Z = 0.78 vetParts (b) through () are worked exactly the same way. All results are summarized as follows. Volume units are cu.cm./mole. SRK, Lig. SRK, Vap. Rackett Pitzer (a) 104.7 1480.7 94,2 1537.8 (b) 110.6 1157.8 98.1 1228.7 (©) 118.2 904.9 102.8 990.4 (@) 1285 7033 109.0 805.0 (©) 1421 1487.1. 125.4 1577.0 (150.7 1189.9 130.7 1296.8 (g) 1618 9478 1374 1074.0 (i) 1771 747.8 146.4 896.0 (146.7 1305.3. 133.9 1405.7 @ 156.9 1035.2 140.3. 1154.3 (i) 170.7 815.1 148.6 955.4 (@ 191.3 6285 160.6 795.8 (m) 612 12489 535 1276.9 (n) 63.5 1003.2 55.1 1038.5 (0) 663 810.7 57.0 53.4 (p) 69.5 59.1 7078 (@) 614 1296.8 54.6 1319.0 (r) 63.9 1026.3 56.3 1057.2 (3) 669 817.0 58.3 856.4 (0) 70.5 652.5 60.6 700.53.40 (a) Propane T, = 369.8-K Py = 42.48-bar = 0.152 T= 404273.15)K T= 31315K P= 13.7I-ber ee Ty = 0.847 Bish Py = 0.323 Te Pe From Table 3.1 for PR: 2 1 a(T;,0) al + (037464 +1 542260 — 0.269920?) ( ll := 0.07779 ‘Y = 0.45724 QP, B(Tr.Pe) = Eq. (3.50) Calculate Z for liquid by Eq. (3.53) Guess: Z = 0.01 Given 2 p(te,P))+ (2-+e-6(ty,P2)}(2+ 6:8 (Te.P) (eet) =FindZ) 2 = 0.049 V Calculate Z for vapor by Eq. (3.49) Guess: Z:=06 Given Z= 1+ (t-.P) ~a(t:)6(T;.P,) 2-p(TE Fi) (Z+6-B(T;,P))(Z+0-B (Ty Py) Zi=Find(Z) Z = 0.766 v 45Parts (b) through (t) are worked exactly the same way. All results are summarized as follows. Volume units are cu.cm./mole. PR, Lig. PR, Vap. Rackett Pitzer (a) 922 1454.5 94,2 1537.8 (b) 97.6 1131.8 98.1 1228.7 (©) 104.4 879.2 102.8 990.4 (@) 113.7 678.1 109.0 805.0 (®) 125.2 1453.5 125.4 1877.0 ( 132.9 1156.3 130.7 1296.8 (g) 143.0 915.0 137.4 1074.0 (b) 1571 7158 146.4 896.0 @ 1294 1271.9 133.9 1405.7 @ 138.6 10023 1403 1184.3 (K) 1512 7828 1486 9554 @ 1702 5973 160.6 795.8 (m) 54.0 1233.0 53.5 1276.9 (n) 56.0 9873 58.1 1038.5 (0) 584 794.8 57.0 853.4 (P) 614 641.6 59.1 707.8 (@ S41 12802 546 1319.0 () 363 1009.7 563 1057.2 () 589 800.5 583 856.4 () 622 636.1 60.6 700.5 463.41 (a)Forethylene, — molwt : 28.054 oe To = 282.3-K mo @ 2= 0.087 T = 328.15-K ‘T, = 1.162 From Tables E.l & E.2: Zo = 0.838 Zg+@Z, 2 = 0.841 i8-ke molwt (b) T= 323.15-K 115-bar r P hres Ty = 1.145 Pes Py = 2.282 Te Pe From Tables E.3 & E.d: Zp = 0.482 126 P-Viotal Z=%+oZ Z= 0493 A 2171 mol ZRT mass := nemolwt mass =60,898kg" Ans. 3.42 Assume validity of Eq. 3.37). 3 V, = 23000 7 , ‘mol Prev RT 3 om? Z; = 0.922 B= —(Z)-1 B = -1.942x 10° — =a 2 p 1) = With this B, recalculate at P, a70.422 Bo := 0.083 — —s Bo = -0.146 Tr Bi ore By = 0.104 a Ty Te + (Bo +o-B)) R— Ans. For an ideal gas: 34 T= 320K P v tek Te 1028s? 3 “i mi Vig = Vere | Viig = 96.769 mol 08, Vionk = 035:m? mig i= tg = 49 7'SB4R Ans. ig mmolwt 0422p = 0.449 16 483 em! Veap = 1318x100 mp = 2341kg Ans. tr T, = 0.701 P, = 0.064 T Te P Pris Po molwt := 58.1232 mol V = 9.469 10° mol Ans. 3.46 (a) T 1, = Ty = 1.091 © P Prem e Py = 2.874 motwt := 30,0722. mol 0.100ZixLo+o2) = 90.87 mol Viotal Methane °= —F ‘molt o P= 20000kPa = PVE ZRTS LRT pT where a a = 29.5482 kg at 4.105 This equation giving T, as a function of Z, and Eq, (3.54) in conjunction with Tables E.3 & E.4 are two relations in the same variables which must be satisfied at the given reduced pressure. The intersection of these two relations can be found by one means or another to occur at about: Tyi= 1.283 and 7, 0.693 Whence T= TrTe T=391.7K or {185-deg Ans. 298.15-K Po 50.40-bar —— @ = 0.087 PY = PpPeV = ZRT R where a= a = 4.675 2 < 50T = Tr = 1.056 Te Whence P= 4675-2 at Ty» This equation giving P, asa function of Z and Eq. (3.54) in conjunction with Tables E.3 & E.4 are two relations in the same variables which must be satisfied at the given reduced temperature. The intersection of these two relations can be found by one means or another to oceur at about: PL79-73 bar Ans. 582 Yio: ° 3.48 myater == 15-kg ve v= 26.667 Mater em Interpolate in Table F.2 at 400 degC to find: P.#.9920:kPa Ans. 3.49 Ty = 298.15-K Tr = 0.977 P) = 2200-kPa Pri = 0.452 Veotat = 0.35:m? o:= 0.100 From Tables El & E.2: Zo Zs lgt+oL, Ti = 1615 493.15-K. 61303.15-K Te i= 304.2-K T= oe Veotat = 0.5-m? Pe 73.83:bar a := 0,224 Bo ~ 0.083 - 2422 Bo = -0.341 16 Tr 172 By = 0.139 — om By = —0.036 Ans. T, = 0.613 Po := 34.0:bar Pr = 0.03 i 3a 3 molwit == 28.0145 Vig = 342-62 Bo = -0.842 62T, Z = 0.987 Rapor Aiyapor = 5.718 10” mol ZRTp ee Final conditions: anol 2-Viig iota “= T-mol + Myapor — i Dtotal Tre Ty = 2.363 359.2bar Use Redlich/Kwong at so high a P. Q = 0.08664 W:=042748 a(T) = Th a(T;) = 0.651 Wea(ty)-R-Te QRTe —_—_———._ (3.42) Sess (3.43) Pe © o.o01m> been oe) Peat 26.737 mol mol Ka A (3.44) = dsoli bar Ans. “VIB Vive) For isobutane: Te = 408.1-K, 3.52 Py = 4-bar 6.48-bar Po ‘Tp = 415KFrom Fig. (3.17): Pry = 245 ‘The final T > Tc, and Fig. 3.17 probably shoutd not be used. One can easily show that _ Pe with Z from Rq. @.54) and Pr ORT ‘Tables E.3 and E.4. Thus 0.181 Z=032 Eq. 3.68): Vo = Vp et Ans. Pr 3.53 For n-pentane: Po i= 33.7-bar py = 0.63-22 em? Ty = 291.15K AIB.ISK Pp t= 120-bar P2 Pa = euuiPe Ty = 0.62 Pri = 0.03 Trg = 0.88 Pra = 3.561 From Fig. 3.17): py = 2.69 i P12 By Eq. 3.65), py = pp 2 Prt Ans.3.84 Forethanol: Ty := 513.9-K = 6148-bar P= 200-bar 3 Ve = 167. ‘mol From Fig. 3.17: Pr Pp Ve imolwt 3.55 For ammonia: Te = 405.7-K T= 293.15K Pe r= 112.8-bar 857-kPa em? Ve = 2.5 Ze = 0.242 mol 0.2887) 1-1) Eq. (3.63): Viiquia = Ve all ) | Bo = 0.627 By = 0.534 x Viiguia = 27-11 ed mol Pre Pp = 3.253 ® = 3.25: Ans. Tet Tr= 0.723 Te P, = 0.076 33 om Vyapor = 2616 : mol Ans. Alternatively, use Tables B.1 & E.2 to get thevapor volume: Ze 0.929 Zj = -0.071 ZLot@Z, Z=0911 Vv, _2ZRT fapor = AV i= apor~ Viguid 10 gal. of gasoline is equivalent to 1400 cu ft. of methane at 60 degF and 1 atm, Assume at these conditions that methane is an ideal gas: f-atm Ibmolrankine R = 0.7302 519.67-rankine P= atm Vv Ve= 1400-8? - nso n= 3.6891bmol RT For methane at 3000 psi and 60 deg: Te: 190.6-1.8-rankine T= 519.67-rankine T, = 1515 Pe = 45.99-bar 3000-psi P, = 4.498 0.012 From Tables E.3 & E.4: Zo = 0819 Zy = 0234 ZL ko+o2 Z = 0.822 56Ans. 3.39.T Calculate the effective critical parameters for hydrogen by equations (3.55) and (3.56) 43.6 ee Te = 30.435K 21.8K L+ 2.016T Pos — 5 __sbar P. = 10.922bar 44.2K 1+ 2.016T P, = 0.294 guess of volume: mol Use the generalized Pitzer correlation 0.422 Bo := 0.083 - Tr Bp = 0.495 By := 0.139 Z= 0823 Ans. Experimental: 2 = 0.08664 Y= 0.42748 ‘Table 3.1 W-a(T) Ta Table 3.1 a(t;) = Eq. G51) 87QP, B(Te,Pr) 2= a Bq. 3.50) Calculate Z, Guess: Zi 09 Given Eq. (3.49) Z(2 + B(Tr.Pe)) Ans. Experimental: Z= 1+B(TesPr) ~a(Ts}B(Tr.Pe} 1.7787 0.012 Te = 190.6K Po := 45.99bar Atstandard condition: T= [to = sy + oe T = 288.706K Pitzer correlations: P:= latm ral T= 1515 es P, = 0.022 i Pe a 7 Bo := 0.083 - 2422 2 139-9172 By = 0.109 1 1 Pr Py Zo 1+ Boe %q = 0.998 1 = Bre 24 = 0.00158 ZRT m Z=Zo+o21 Z=09% Vps a Vy = 0.024 P mol an 5 | 5 (a) At actual condition: T =| (50- 325 + ila P := 300psi Pitzer correlations: eee Tel T, = 1486 P, = 0.45 Te Bo = -0.141 580.172 By = 0.139--— By = 0.106 Tr Pr Pr Zo = 1+Bo Tr Zo = 0.957 = Bee Zy = 0,0322 3 Z = 0.958 V2 = 0.00109 7 mol V2 ete a2 915 10°. Ans. 24 Vi an day © D = 22.624in A= 0.259m" wis Ans. ole3.62 0.012 0.087 O41 0.140 0.152 0.181 0.187 0.19 0.191 0.194 0.196 02 0.205 021 021 0.212 0.218 0.23 0.235 0.252 0.262 0.28 0.297 0.301 0.302 0.303 0.31 0.322 0.326 0.286) 0.281 0.279 0.289 0.276. 0.282 0.271 0.267 0.277 0.275 0.273 0.274 0.273 0.273 021 0.272 0.275 0272 0.269 027 0.264 0.265 0.256 0,266 0.266 0.263 0.263 0.26 0.261 Use the first 29 components in Table B.1 sorted so that «o values are in ascending order. This is required for the Mathead slope and intercept functions, tope(w.Zc):= (-0.091) intercept(«,Zc) = (0.291) R i= cor(w,Zc) = (0.878) R*= 0.771Chapter 4 - Section A - Mathcad Solutions 4.1 (a) Ty = 473.15-K T= 1373.15-K n= 10-mol ForS0%: A= 5699 B=0801107 C= icpHi(473.15,1373.15,5.699, 0.801103, ICPH := 5.654-10°.K AH:=RICPH Q:= AH GaN Ans. (b) To := 523.15-K T }473.15-K ‘= 12-mol For propane: A 1213 B= 28785107? C= -8.824-10"° rep (523.15, 1473.15, 1.213, 28.785-107 =8.824-107 °,0.0) = 1.947-10° ICPH := 1.947-10%K AH := R-ICPHL Q:=n-AH QS 194K 107K Ans. 42 (a) To = 473.15-K n= 10-mol — Q:= 800-K 3 6 Forethylens Ass 1424 pe AAROEIOT™ 4.39210" K ev 1 = 2 (guess) Given Bo 2(2 C133 Qe {| A-t06 a1) Bape? | +S (2- | = Find(t) = 2.905 T:=tTo 13745K Ans, (b) Tg := 533.15-K n= 15-mol Qs 2500-KI 31.630-10°* K For I-butene: A := 967 iB c 613 (guess) Given Qen {| a-to6-0 +E ne -]-Snie ee ) Find(x) 7 = 2.652 3.8K Ans. (©) To == 500-degF n= 40-lbmol Q:=10°BTU Values converted to SI units To = 533.15K 1.814x 10'mol Q = 1.055 x 10°ks 14.394:10- 4.392.107 K KR For ethylene: A 424 c= 2 (guess) Given t= Find(t) 1 = 2.256 T:=tTo Convert given values to SI units Vv = 7.079m9 = (T— 32degF) +273.15K To = (To ~ 32degh) +273.15K T = 1187.37K To = 323.15K 66.985 mol A= 3355 B= 057510°° 0.0 =D=-0.016-10° 1ePh{323.15,773.15,3355,0.575-10" 3,0.0,-0.016-108) = 1688.702 @ICPH := 1648.702-K AH:=R-ICPH Q 465% 1 BTU Ans. 4.4 molwt := 1001-22 To =.323.15-K 153.15-K mol 0000: z= 20000-kg n= 9.99 10'mol mohwt For CaCO3: Ais 12572 B=263710° =D = -3.120-10° repHi(323.15, 1153.15, 12.572,2.637-107°,0.0,-3.120-10°) = 113554 ICPH := 11355.4K AH ss -ICPH Qs mal 4314% 10K) Ans. 4.7, Let step 12 represent the initial reversible adiabatic expansion, and step 23 the final constant-volume heating. Ty = 298.15K T3 = 298.15-K Py = 121.3-kPa P. Pp = 101.3-kPa P3 == 104.0-kPa T2 = T3 = 3 cp = 30.bule (ques) T) = 290.41K molK Ans, 33.70 309.2 30.25 341.9 48.98 | 353.2 |K 41.06 es 40.73 353.9.i AH yp is the given Peers ee a SH Me valet NPA emurmal ty x EK gy Te boiling point. Te Te 366.3 357.2 0.635 0.658, 366.1 336.7 0.587 0.674 AH = | 433.3 [3939/2 1 -| 053 | Te =| 0.028 aaa) 3632.) 0.504 0.649 392.5 358.2, 0.539, 0.639 (a) By Eq. (4.13) (b) By Bq. (4.12): AH, =|4.10. The In P vs. 1/T relation over a short range is very nearly linear. Our procedure is therefore to take 5 points, including the point at the temperature of interest and two points on either side, and to do a linear least-squares fit, from which the required deriva Eq, (4.11) can be found, Temperatures are in rankines, pressures in psia, volumes in cu ft/bm, and enthalpies in Btu/lbm. The molar mass M of tetrafluoroethane is 102.04, The factor 5.4039 converts energy units from (psia)(eu ft) to Btu. (a) T := 459.67+5 AV := 1.934~0.012 +e 18.787 7 21.162 0 1 Data: P= | 23.7 = =— y= h(P} ais P= [23767] t=] S| x= oe = h(n) 26617 10 29.726 Is slope = slope(x,y) slope = ~4952 (-P). 3 aPaT =: slopdPdT = 0.545 _ Tay-dPaT “3.4039 AH = 90,078" Ans. ‘The remaining parts of the problem are worked in exaetly the same way. All answers are as follows, with the Table 9.1 value in (): (a) AH = 90.078 (90.111) (b) AH = 85.817 (85.834) (©) AH = 81.034 (81.136) (@) AH = 76.007 (75.902) (©) AH = 69.863 (69,969) 654a 119377 3364 34.72 334.3 32.082 |-SE ty 1=/ 5126 |K Py =| 80.97 bar Ty =| 397.9 | 153.822 356.4 45.60. 349.8 AlTis the valueat “Hep is the given pony O deg value at the normal Typ = 223:15K boiling point. Te 2109 246.9 0.509 0.623 J AH =| 118952 Atle :=| 10995 |. ty =| 0533 | Ti =| 0.659 gm 2178 1942 0491 0.629 (a) By Eq. (4.13) AHexy — 100% This is the % error ‘AHexp( -2,732.016 J (g) -105,140 J (hy -38,292 J () 164,647 (i) -48,969 5 (&) 149,728 F () -1,036,036 J (m) 207,436 J (s) -492,640 5 (0) 109,780 J (u) 235,030 J (v) -132,038 J (05) -1,807,968 J (x) 42,7205 (y) 117,440 @) 175,305 J 4.22 ‘The solution to each of these problems is exactly like that shown in Example 4.6. In each case the value of AH029g is calculated in Problem 4.21, Results are given in the following table. In the first column the letter in () indicates the part of problem 4.21 appropriate to the AH? value. TK 4A | 103 4B | 106 ac | 105 Ap | IDCPH | anos (@ [873.15 | -5.871] 4.181 | 0.000 | -109,795 (6) [773.15 1.861] 3.394 | 0.000 -900,739 | (p_| 923.15 6,048 | -9.779 | 0.000 “2,716,381 (i) [973.15 9.811 | -9.248 [2.106 189,87 @_| 583.15 9.523 11,355 | -3.450. _| 683.15 0.441 0.004 | 0,000. (mj | 850.00 4.575 -2.323 | 0.000 (| 1350.00] -0.145| 0.159 | 0.000 fo) | 1073.15 -1.011 -1.149 | 0.000 @ [M315 | -1424| 1.601 | 0. ()_| 733.15 4.016 | -4.422 | 0.991 117,204 fw) | 750,00 7.297 | -9.285 | 2.520 72] 247,202 | ‘6y {900.00 2.418 | -3.647 | 0.991 34] 128,504 | (w) | 673.15_| 2.586} -4.189 | 0.000 “1,803,784 | 648.15 0.060} 0.173 | 0.000 22; 6) _{ 108: 4.766 129,628 78ition of a combination of Eqs. (4.18) & (4.19) with evaluated parameters. In each case the value of AH(9g is calculated in Pb. 4.21, The values of AA, AB, AC and AD are given for all cases except for Parts (e), (g), (h), (k), and (2) in the preceding table. Those mi follows: [PartNo.[ AA [103.ap [1064c | 10-S.ap | © -7.425| 20.778 | 0.000 3.737 @ 3.629 | 8.816 | 4.904] 0.114 (h) -9.987| 20.061 | -9.296 1.178 ®) 1.704} -3.997 | 1.573] 0.234 @ -3.858| -1.042] 0.180 [ 0.919] 3 150.1082 day 424g atm (60-32) Sk +27, ISK T= 288.71K P ‘The higher heating value is the negative of the heat of combustion with water as liquid product. Calculate methane standard heat of combustion with water as liquid product: CH, +20, > CO, +28,0 Standard Heats of Formation: i Ajo? = 02 = Orel = 285830. mol A co2 + 2-AH p201ig - AH icra — 2-AH p02 HigherHeatingValue := -AH, AH, = -8.906x 10°. mol Assuming methane is an ideal gas at standard conditions: P gol Sq 1.793 x 10°—— nae a a 74.25 Caleulate methane standard heat of combustion with water as liquid product Standard Heats of Formation: CH, + 20; ~> CO; +2H,0 3 AHigonig = -74520—— J Alcon = ~393509 Allgcue = AHyco2 + 2AM pong ~ AHscHs ~ 2-AH 02 J AHecH4 = ~890649— mol Calculate ethane standard heat of combustion with water as liquid product: Standard Heats of Formation: C,H, + 7/20; -> 2CO, +3H,0 Heong == ~83820—— mol AllecaHs = 24H ico2 +3-AHpH201iq ~ AHicaHs ~ 1560688 ‘mol ABecoH6 = Calculate propane standard heat of combustion with water as liquid product Standard Heats of Formation: CsHs + $0; ~> 3CO, +4H,0 1046802 mol ABicsus AH osHe = 34H coz + 4 AH DOI ~ AHacsHe ~ SAH yo? ease Gas b) has the highest standard heat of combustion. 784.26 4.28 2H2 + 02=2420() C+ 02=CO2%g) N2(g)+2H2(g)+C(s)+1/202(g)=(NH2)2CO() AHy99 == AH, + AH + AH ‘ANog On the basis of 1 mole of C10H18 (molar mass = 162.27) Q = -43960-162.275 Q=-7.133x 10°F This value is for the constant-volume reaction: C1OHI8(1) + 14,502(g) = 10CO2(g) + 9H20() Assuming ideal gases and with symbols representing total properties, Q= AU = AH-A(PV) = AH-R-T-Angas T= 208.15-K Angas ‘= (10 14.5)-tnol -7.145 x 10°F AH = Q4R-T-Atggs AH This value is for the constant-V reaction, whereas the STANDARD reaction is at const. P.However, for ideal gases H = f(T), and for liquids H is a very weak funetion of P. We therefore take the above value as the standard value, and for the specified reaction: CIOHI8(1) + 14.502(g) = 10C02(g) + 9H20) AH 9H20(\) = 9H20(g) AHyap = 9-44012-5 ‘C1OH18(1) + 14,502(g) = 10CO2(g) + 9H20(g) yap, AHbog = 6748436) Ans. 794.29 FURNACE: Basis is 1 mole of methane burned with 30% excess air. CHa + 202 = CO2 + 2H20¢@) Entering: Moles methane =n = 1 Moles oxygen ng = 2-13 ng = 2.6 Moles nitrogen ny 15 26 2 ng = 9.781 1 Total moks of dry gases entering n= my +m. +15 13.381 At 30 degC the vapor pressure of water is 4.241 kPa, Moles of water vapor entering: 4.241 —_ 42H 13.381 = 0.585 4 701.325 - 4241 7 Leaving: C021 mol a) 120 ~ 2.585 mol @) 2.6-2= 0.6 mol @) Nz --9.781 mol @ By an energy balance on the furnace: Q = AH = AHy9g + AHp For evaluation of AHy we number species as above. 1 5.457 1.045 3AT0| | 1490 | A e 7 10" 06 3.639 0.506 9.781 3.280. 0.593 4 Ris 8.314 Swi pe YB A= 48.692 B = 0.010897 80‘The TOTAL value for MCPH of the product stream: Mcpit(303.15, 1773.15, 48.692, 0.897.107, 0.0,-0.5892.105) MCPH AHp := R-MCPH-(1773.15 — 303.15) From Example 4.7: AHgog := ~802625 Q = AHp + AH29g QF 9.895 11 9.89511 “10,61 Ans. HEAT EXCHANGER: Flue gases cool from 1500 degC to 50 degC. The partial pressure of the water in the flue gases leaving the furnace (in kPa) is m2 pp. 101.325 pp = 18.754 ny tn +n3 ng ‘The vapor pressure of water at 50 degC (exit of heat exchanger) is 12.34 kPa, and water must condense to lower its partial pressure to this value. Moles of dry flue gases: n nengtng n= 11.381 Moles of water vapor leaving the heat exchanger: 1234 101.325 — 12.34 ‘Moles water condensing: An mi ng = 1.578 2.585 1.578 Latent heat of water at $0 degC in J/m« AMEgg := 2382.9-18.015 ‘Sensible heat of cooling the flue gases to 50 degC with all the water as vapor (we assumed condensation at 50 degC): MCPH(323.15,1773.15, 48.692, 10.897. 10" >, 0.0, -0.5892-10°) = 60.01086 MCPH := 60.01086 Q = R-MCPH-(323.15 ~ 1773.15) - An-AHs9 Q''=766;677:] Ans. at4.30 4NH13(g) + 802(g) = 4NO(Q) + 6H2O0(@) BASIS: 4 moles ammonia entering reactor Moles 02 entering = (5)(1.3) = 6.3 Moles N2 entering = (6.5)(79/21) = 24.45 ‘Moles NH3 reacting = moles NO formed = (4)(0.8) = 3.2 ‘Moles 02 reacting = (5)(0.8) = 4.0 ‘Moles water formed = (6)(0.8) = 4.8 ENERGY BALANCE: AH = AHg + AHg9g + AHp = 0 REACTANTS: 1=NH3; 2-02; 3-N2 4 3,578 3.020 0,186 65 | A]3.039) B=} 0506|-10? D=| -0.227 j-10 24.45 ) 3.280, 0.593, 0.040 ea: A Svai B yn Bi D Yi 7 i i A= 118.161 B= 0.02987 D = -1.242x10° TOTAL mean heat capacity of reactant stream: McpH(348.15,298.15, 118.161, 0.02987, 0.0,-1.242-10°) = 126.61632 MCPH := 126,61632 AHg := R-MCPH-(298.15 ~ 348.15) The result of Pb. 4.21(b) is used to get AHggg = 0.8-(-905468) PRODUCTSi=NH3; 2: 2; 3-NO; 4-20; 5=N2 os 3.378 3.020 0.186 25 3.639 0.506 0221 32 A= |3.387 0.628 |-1073 0.014 |-10° 48 3.470 1.450 0.121 24.45 3.280. 0.593) 0.040 82A Yiwai A= 119.65 B= 0.027 D= 8.873% 10" Yai D Yer By the energy balance and Eq. (4.7), we can write: To:= 298.15 t= 2 (guess) Given tisFind(t) 9 1328300 Tis Ty K-t Ans, 431 C2H4(g) + H20(@) = C2HSOH() BASIS: 1 mole ethanol produced Energy balance: ayy = Q = AHg + AHgog AHp9g := 277690 — (52510 - 241818) AHy9g = -8.838x 10" Reactant stream consists of 1 mole each of C2H4 and H20. 1.424 14394) 4.392 As B H10-* C= 3.470 1.450 0.0 A ae Yai Yee =-4322x10° D S 00 os > jh’ 0.121 Yd Lixo A=4894 B= 0.01584 McPH(298.15,593.15,4.894,0.01584,~4.392-10"§,0.121-109) = 11.1192 83MCPH := 11.1192 Ag := R-MCPH:(298.15 ~ 593.15) AH = -2.727« 10" Q = (AHR + AHo98}-5 £5115683) Ans. 4.32, One way to proceed is as in Example 4.8 with the alternative pair of reactions: CH4+ H20=CO+3H2 ‘AlLyogq = 205813 CH4 + 28120 = CO2 + 4112 AFLgogp += 164647 BASIS: 1 mole of product gases con! CO; & H20 0.6275 mol H2 g 0.0275 mol CO2; 0.1725 mol Entering gas, by carbon & oxygen balances: 0.0275 + 0.1725 = 0.2000 mol CH4 0.1725 + 0.1725 + 2(0.0275) = 0.4000 mol H20 AHg9g := 0.1725-AHz9gq + 0.0275: AH 9gb AHgog = 4.003 x 10" 02 0A 1.102 9.081 2.164 x ( ) oe jo cs 10° ® b= (.°° Ji’ 3.470 1.450. 0.0 \o.121) A ya AUB = Bi Yc D yn Dj LR8 B= 2396x107? C= -4.328x107 Da 484% 10? ‘The energy balance is written Q= AHR + AHp9g + AHp. REACTANTS: 1=CH4;2=H20 i 1cPHH(773.15, 298.15, 1.728,2.396-10 4.3310 ,4,84-10°) = -1377.435 137.435 AHR := RICPH AH = -1.145x 104 ICPH = PRODUCTS: CO; 3=H20; =H?4 B= 6.397% 10 D = 3.579% 10° rcpi{298.15,1123.15,3.370,6397-10"4,0.0,3.579-108) = 3164.293 ICPH := 3164.293 ‘AHp := RICPH ‘AHp = 2.631 10" Q = (Hp + 4Ha98 + AHp)-J QE 54886) Ans. 4.33 CH4 +202 = CO2 + 2H20(g) C2H6 + 3.502 = 2CO2 + 3H20(@) AFg9gp = — 1428652 BASIS: 1 mole fuel (0.75 mol CH4; 0.25 mol C2H6) burned completely with 80% xs. air. 02 in = 1,8§(0.75)(2) + (0.28)3.5)] = 4.275 mol N2 in = 4.275(79/21) = 16.082 mol Product gases: CO: 1S + 2(0.25) = 1.25 mol H20 = 2(0.75) + 3(0.25) = 2.25 mol. 02 = (0.8/1.8)(4.275) N2= 16.082 mol AH 9g != 0.75-AHl9gq + 0.25-AHpogp Q:=-8:10° 9 mol Energy balance: Q = AH = AHz9g+AHp AH = Q= Ay 3 PRODUCTS: 1=CO2; 2=H20; 3=02; 4=N2 1.25 5.457 1.045 “1.157 2.25 3.470 1450} 3 o121 | 5 = A B K10-* D 10" 19 3.639 0.506 16.082 ) 3.280 0.593, 854.34 As Sima B Yves A=74292 B= 0015 D = 9.62% 10" By the energy balance and Eq. (4.7), we can write: To = 303.15 t= 2 (guess) ) t= Find(t) eee Given Q=AHg9¢ = RY A-To-(t = 1) + To (: = L788 TH542K Ans. BASIS: 1 mole of entering gases containing 0.15 mol SO2; 0.20 mol 02; 0.65 mol N2 S02 +0.502=S03 Conversion = 86% S02 reacted = SO3 formed = (0.15)(0.86) = 02 reacted = (0.5)(0.129) = 0.0645 mol Energy balance: AH773 = AHg + AH29 + AHp Since AHy and AHy cancel for the gas that passes through the converter unreacted, we need consider only those species that react or are formed. Moreover, the reactants and products experience the same temperature change, and can therefore be considered together. We simply take the number of moles of reactants as being negative. The energy balance is then written: AH773 = AHy9g + SH yet AHg9g = ~395720 = (~296830)}-0.129 1: $02; 2: 02; 3: SO3 0.129 5.699 0.801 =1.018 ~0.0645 | A=] 3.639] B:=10506}10-9 D3=| -0.97 |-10° 0.129 8.060. 1.056 ~2.028A= 0.06985 B= 2.58% 10" D McPH(298,15,773.15,0.06985,2.58-10" 7, 0.0,-1.16-104) = 0,019666 MCPH := 0.019666 AFIngt == R-MCPH(773.15 ~ 298.15) AH773 = (AH295 + AHpet)-J Ans. 4.35 CO(g) + H20(g) = CO2g) + H2g) BASIS: 1 mole of feed consisting of 0.5 mol CO and 0.5 mol H20. moles H20 reacted = moles CO2 formed = moles H2 (0.6)(0.5) = 0.3 Product stream: moles Ct moles CO2 = moles H2 formed = moles H20 = 0.2 3 Energy balance: Q= AH = AHR + AHg9g + AHp = 0.3:[-393509 — (-110525 ~214818)] __ AHy9g = -2.045 x 10° CO 2: B20 ( .) As 3.470. 0557) 3 0.031) 5 Bs -10 Ds 10 1.450, 0.121 D -> Di 004x107 D = 4.5x 10° McPH(298.15,398.15,3.423, 1.0035-1073,0.0,0.045 10°) MCPH := 3.8103 3.8103 Aly := R-MCPH.(298.15 ~ 398,15) AH = ~3.168« 10° Products: 1:CO 2: H20 3:CO2 4:H2 8702 3.376) 0.557 =0.031 B 3.470 1.450 os 0.121 a As B ho Des -10° 5,457 1.045 1.157 03 3.249 (oa 0.083 Ac x -Ay OB YB D ya Dj i i 7 A= 3.981 B=84isxi0* —D=-3.042x104 McPH(298.15,698.15,3.981,0.8415-10"°,0.0,-0,3042-10°) = 4.25405 MCPH := 4.25405 ‘Alp = R-MCPH- (698.15 ~ 298.15) AHp = 1415 10" Qs (Alig + AHp9g + AHp)- ‘Ans, 436 BASIS: 100 tbmol DRY flue gases containing 3.00 Ibmol CO2 and 11.80 Umol CO x Ibmot 02 and 100-(14.8-x)= 85.2-x Ibmol N2. The oil therefore contains 14.80 tbmol carbon;a carbon balance gives the mass of oil burned: 12.011 0.85 14.8. Ibm = 209.133 Ibm The oil also contains H20: ZO O0} pmol = 0.116ibmot 18.015 Also 20 is formed by combustion of H2 in the oil in the amount 209.133-0.12 Ibmol = 12. sig tbe! 48 lbmol Find amount of air entering by N2 & 02 balances. N2 entering in oil: 0.02 © pmol = 0.149 bmol tbmol N2 entering in the air=(85.2-x)-0.149 85, 88Imo! 02 in flue gas entering with dry air = 3.00 + 11.8/2 + x + 12.448/2 15.124 + x Ibmol (C02) (CO) (02) (H20 from combustion) ‘Total dry air =N2 in air + O2 im air = 85.051 - x + 15.124 + x = 100.175 Ibmol Since air is 21 mol % 02, = ISM +x 100.175 0.21 (0.21-100.175 ~ 15.124)-Ibmol__x = 5.913 Ibmot 02 in air = 15.124 + x = 21.037 Ibmols N2 in ai 5,051 - x = 79.138 Ibmoles N2in flue gas = 79.138 + 0.149 = 79.287 Ibmols (CHECK: Total dry flue gas = 3.00 + 11.80 + 5.913 + 79.287 = 100.00 Ibmol] Humidity of entering air, sat. at 77 degF in Ibmol H2O/Ibmol dry air, P(sat)=0.4594(psia) 0.4594 14.696 — 0.4594 Homo! H20 entering in air: = 0.03227 0.03227-100.175-Ibmol = 3.233 Ibmol If y = Ibmol H20 evaporated in the drier, then Ihmol H20 in flue gas = 0.116+12.448+3.233+y 5.797 + y Entering the process are oil, moist air, and the wet material to be dried, all at 77 degF. The "produets” at 400 degF consist of: 3.00 lbmol CO2 11.80 Ibmol CO 5.913 Ibmol O2 79.287 Ibmol N2 (15.797 + y) Ibmol H20(g) Energy balance: Q = AH = AHy9g + AHp where Q = 30% of net heating value of the oil: a9= -03-19000- 22. 209.13:1bm Ibm 1.192 10°BTU Reaction upon which net heating value is based: OIL + (21.024)02 = (14.8)CO2 + (12.448 + 0.116)H20(g) + (0.149)N2 =19000-209.13-BTU ‘AHg9gq = -3.973 x 10°BTU ‘To get the "reaction" in the drier, we add to this the following: (11.8)CO2 = (11.8)CO + (5.9)02 AH 988 AHgggp = 11,8:(-110525 + 393509)-0.42993-BTU. (yH20(g) Guess: y = 50 Allggge(9) := 44012-0.42993-y-BTU. (y)H2000 (The factor 0.42993 converts from joules on the basis of moles to Btu on the basis of lbmol.] Addition of these three reactions gives the "reaction" in the drier, except for some 02, N2, and H20 that pass through unchanged. Addition of the corresponding delta H values gives the standard heat of reaction at 298 K: AHp9g(y) #= AHo9gq + AH29gp + AH29ge(¥) For the product stream we need MCPH: 1:CO2 2: CO 3:02 4:N2 5: H20 To = 298.15 R= 1,986 T wee T = 477594 3 5.457 1.045 1.157 18 3376 0.587 0.031 ny) =| 5.913 A=] 3.639 0.506 |- 0.227. |-10" 79.218 3.280 0.593 0.040 15.797 +y. 3.470, 1.450 0.121 LS AQ)= Vawra; BO) =YawrB: Do = Yor; 1 = t= 1602 Cply) = R [aoe Pao +420 2 Ty 90Te = 562.2K 8.98bar — Z_ 25 0.271 353.2K That Ty = 0.628 Pe 0.02 Generalized Correlations to estimate volumes Vapor Volume 0.422 PO OURS eet Eq. (3.61) Ty By = 0.139 - By = -1.073 Eq. (3-62) Py Pr Ze lsBox obra Z= 0967 ZRTy 3 Ves V = 2.838% 19° - mol Liquid Volume 257 3 Vogt = Vere) Eq. 3.63) Vat = 96.807" mol ‘Combining the Clapyeron equation (4.11) AH = T-AV-4 Pye a eae with Antoine's Equation Pay =e ™C gives AH ® T-AV- (toy 675 AV=V=Veap AV = 2.829 19° mol B= 277378 C= 53.00 Answers for parts (b)-(e) () Ant = 36.262 © mol ( an=32.278 mol (@) an=28948 2 mol (© aH =33.838 mol 4.13, Let P represent the vapor pressure. T = 348.15-K 100-kPa ( Given hl ee 5 48.157543 - kPa} ind(P) dPdT := P. Ree P = 87.396KPa ‘AH = 31600. 68 5622.7-K ((5622.7K _ 4.70504) (guess) 4.70504: a T joule molClapeyron equatio V= vapor molar volume. V = Viq+ SY T-apaT F439: Bn v{2¥ 4) Ans. 38): et } 4.14 (a) Methanol: Ty = 512.6K 0.97bar Ty = 337.9K AL: 13.431 -81.28-10~ = 131.1310" © fee q CpL(T) =| AL+ 14 = js eRe Ay =2211 By := 12216-1077 Cpy(T) = (megeres re yee Trsat = ki AHg = 38.301 — mol eikd Ally = 35.645 mol 6912 Text 7 encnet vany+ | cey(naT alt= 49.38" 1 Tost a nes oo mel Q=n-AH ‘Ans. ir (b) Benzene: aH, = 28.273. 55.296 2. moi mol J Ky (© Toluene AH, = 30.625— AH = 65.586 — mol mol 4.15 Benzene T.:= 5622K Pg Tisat 2 451.7K — Tosat = 358.7K Cp Estimate AHy using Riedel equation (4,12) and Watson correction (4.13) Tosat Ten = 0.628 Trasat Trasat = 0.638 30.5882 mol aly = 30.285. mol is adiabatic and isenthalpic. Assume the throttling proces: Guess vapor fraction (x): x := 0.5 Given Cp-(Tisat— Tasat) = XAHy x= Find(x) KE 04982 Ans. 189.4-K 308.3-K 4.16 (a) For acetylene: T, 61.39-bar Ty, T= 298.15-K 70Th T rut Tv ned erat T= 0087AH, = 1691 mol any = 6638-2. mol (b) For 13-butadiene: Agog = 88.5 mol ig (©) For ethylbenzene: AHy5g = —12.3—— mol Ws (@) For n-hexane: AH5g = -198.6— mol KI (©) For styrene: AFg9g = 103.9-— mol 4.17 Ist law: dQ = dU -dW = CydT+P-dV A) Ideal gas: PV=SRT and PdV+V-dP = RdT Whenee V-dP = R-dT- P-dV @) Since p-V? = const then P.8-VO"Lav. from which V-dP —Pb-dV ‘Combines with (B) to yield: Pav = So 14.18 R Combines with (A) to give: AQ = Cyat + a or dQ= Cpar-Rars RH which reduces to Since Cp is linear in T, the mean heat capacity is the value of Cp at the arithmetic mean temperature. Thus Tam ‘= 675 Cem 85+ 0.57:10"?-Tam) Integrate (C): 50K Ans, For the combustion of methanol: CH3OH(g) + (3/2)02(g) = CO2g) + 2H20(g) AHQ98 393509 + 2-(-241818) — (-200660) AH 9g = ~676485 For 6 MeOH: Ans, For the combustion of 1-hexene: (COH12(g) + 902(g) = 6CO2(g) + 6H20(g) 724.19 AHg9¢ := 6-(~393509) + 6(-241818) - (-41950) 27 Ams. AHg9g = ~3770012 AHao@ ='=3,770,01 ‘Comparison is on the basis of equal numbers of C atoms. C2H4 + 302 = 2CO2 + 2H20(g) Bog = [2-(-241818) + 2-(-393809) ~ $2510]. — mol mple 4.7. However, with simpler to proceed differently. Parts (a) - (d) can be worked exactly as Mathead capable of doing the iteration, Index the product species with the numbers: 1= oxygen 2= carbon dioxide 3 = water (g) 4= nitrogen (a) For the product species, no exeess air: 0 3.639 0.506) ~0.227 2 5.487 1.045 | 10-3 “137 2 3.470 1.450 | K oat 11.286, 3.280, 0.593, 0.040. 4 A Yai B: Sg A = 54.872 B= 00125 D = ~1.621«10°K oT cp For the produets, Ape R | FedT Tos 298.15K Jig The integral is given by Eq. (4.7). Moreover, by an energy balance, Algo + AHp = 0 3t= 2 (guess) B Given ~AHg9g = R- [4 To(t-1)+ ; 92 Find(z) += 8497 Tis Tot = EE 25335K Ans. Parts (b), (¢), and (d) are worked the same way, the only change being in the numbers of moles of products. 6) nq, = 14.107 198.6K Ans. © ho, = Rn, = 16.929 T= 1950.9K Ans. (a) no, = 3.0 Ng, = 22.571 T= 1609.2K Ams. (©) 50% xs air preheated to 500 degC. For this process, Alb + AH 299 + AH AHgir = MCPH-(298.15 ~ 773.15) For one mole of air: McPHi(773.15,298.15,3.355, 0575-10 For 4,5/0.21 = 21.429 moles of air: R-MCPH-AT [aie = 21.429-8.314-3,65606-(298.15 — 773,15) mol b = i AH gi, = -309399 mol ‘The energy balance here gives: AHyog + Agi, + AHp = %1s 0.227 2. 1,157 a Ds -10°-K? 2 0.121 16.929, 0.040 Ds domi A= 78.84 Be oie D ==1.735 x 10°K? t= 2 (guess) Given —AH998 - AHair = R} A-To-(t ~ 1) 2 tele? — 1)... D +P To tis Find(z) 1 = 7.656 Tis Tp Kt 420 n-CSH12 + 802 = 5CO2 + 6H20(1) By Eq, (4.15) with data from Table C.4: Ans. 4.21 The following answers are found by application of Eq. (4.15) with data from Table C4, (a) -92,220 5 (n) 180,500 5 (b) -908,468 J (0) 178,321 5 (c) -71,660 3 (p) -132,439 J (a) -61,980 5 (@) 44,3703 (©) -367,582 J () -68,910 J 75437 4.38 Given Cp(y)-(400 - 77)-BTU = Q- AH99(9) Find(y) y = 49.782 (Ibmol H20 evaporated) = 4388. (lb H20 evap. per Ib oll burned) DORIS oe ‘a Whence One mole of product gas containing 0.242 mol HCN, and = 0.379 mol each of N2 and C2H2. The energy balance is Q= AH = AHa93 + AHp ‘AHy9g := (2-135100 — 227480). a AHiggg = 5.169% 10° Products: 0.242) 4.736 1.359 0.725 0379| A= /3.280] B:=/.0.593 10> D =| 0.040 |-108 I 6.132, 1.952. =1,299 3 A yn Dj Sra B ye Bi D i R:= 8314 A=47133° B= 12934x10> Dp = -6.526x 10" McPH(298.15,873.15,4.7133, 12934-1073, 0.0, -6.526-104) 22010 MCPH := 5.22010 AHp := R-MCPH-(873.15 ~ 298.15)J AHp = 2.495 x 10 Q := AHgog + AHp GQ S304] Ans. BASIS: 1 mole gas entering reactor, containing 0.6 mol HCI, 0.36 mol 02, and 0.04 mol N2. HC reacted = (0.6)(0.75) = 0.45 mol 4HCKg) + 02(g) = 2H20() + 2CL(g) For this reaction, 31Agog #= 2-(-241818) ~ 4-(-92307) AHg9g = -1.144 x 10° Evaluate AHgp3_ by Eq. (4.21) with To s= 298.15 Ts 823.15 R:= 8314 1:20 2: C2 3: HCI 2 3.470 145 0.121 4.442 0.089 3 0.344} 5 A= Be 10 10" 3.156 0.623 0.151 =I 3.639 0.506, 0.227 “4 AA > a AD = SnD; 5 a AA =-0439 AB = 8x 10 AD = -8.23 x 10 8.23.10) = -0.72949 MDCPH(298.15,823.15,-0.439,8.0-107 MDCPH := ~0.72949 AHgp3 := AHy93 + MDCPH-R-(T - To) AHg93 = 117592 Heat transferred per mol of entering gas mixture: AHg23°5 Q = ‘0.45 ‘Ans. 4 439 CO2+€=2C0 @ 2C + 02=2C0 & Eq. (4.21) applies to each reaction: For (a): 2 3.376 0.557 nef-1] Acs/ 1771 o7m|io> Dp -10° ah 5.457, 1.045 AA nA; AB Bj AD » “Dj a 92AA=-047 = AB=-7.02x10* AD = 1.962% 10° MpcpHi(298.15,1148.15,-0.476,-7.02-10"*,0.0,1.962-108) = -0.410505 0.410505 AH29gq + R- MDCPHe-(1 148.15 ~ 298.15) SH 148q = 1.696% 10° MDCPH, SH 148 3.376 0557 0.031 3.639} B:=| 0.506 |-107* — D:=| -0.227 |.10° L771 0.771 0.867 , AA De aD = Sn Dj AA = 0.429 AB=-934x 1074 AD = 1.899 10° MDCPH(298.15, 1148.15,-0.429,-0.934.10"3,0.0, 1.899.10°) = -0.549680 MDCPHp := -0.549680 AH} tagh °= AHoogp + R-MDCPH (1148.15 — 298.15) AH tap = 2.249 10° The combined heats of reaction must be zero: nco,'AHy 48a +0,°AH) 1480 = 0 Define: r r= 1327 For 100 mol flue gas and x mol air, moles are: Flue gas, Air Feed mix coz 12.8 0 12.8 co 37 0 37 93,oz 34 o21x 54+ 0.21x N2 781 0.79. 78.1 + 0.79x 128 Whence in the feed mix: p= ——__ 5.44021 19.155mol Flue gas to air ratio= Ans. Product composition: neo #= 3.7 +2-(12.8 + 5.44 0.21-19.155) ng = 48.145 ON, = 78.1 +.0.79-19,155 ON, 93.232 Mole % CO= Mole % N2= 4.40 CH4 +202 = CO2 + 2H20(@) AHg9gq = ~802625 CH4 + (3/2)02 = CO + 2H20(g) AH 9gp *= ~519641 BASIS: L mole of gas consisting of 0.94 mol CH4 and 0.06 mol N2 Air entering contains: 1.35-2.0,94 = 2.538 mol O2 mol N2 ‘Moles CO2 formed by reacti 0.94-0.7 1.058 Moles CO formed by reaction = 0,94-0.3 = 0.282 J AHa9g = (0.658-AHa994 + 0.282-AHaog5} AHo9g = -6.747 x 10° mol mol 4Moles 1120 formed by reaction = —_0,94.2.0 = 1.88, Moles 02 consumed by reaction= 2.0.658 + 3 0.282 = 1.739 Product gases contain the following numbers of moles: 0.658 0.282 1.880 2.538 - 1.739 = 0.799 9.548 + 0.060 = 9.608 0.658 5.457 1.045. 0.282 3.376 0.557 n:=| 1.880 As=|3470] B=] 1.450 |-1077 0.799 3.639 0.506 9.608. 3.280 0.593 R:=831 A= 454881 B= 9,6725x 10 mohK McPH(298.15, 483.15,45.4881,,9.6725-107?,0.0,-3.396-10") = 49.03001 MCPH := 49,03091 J Ap := R-MCPH-(483.15 ~ 298.15)-K AHp = 7.541 x of mol Ki Energy balance: Adley = Alz99 + AH AFlyy = ~599.252-— mol kg AH yp9-mdoty20 + Sy ndotjgel = 0 mdoty20 = 34.028. see kT From Table C.1: AH29 '= (398.0~ 104.8). ‘B AH} 29'mdotr20 ah alin dott = 16.635 6.635— see dott 95Volumetric flow rate of fuel, assuming ideal gas: ndotfyet"R:298.15-K 101325-Pa Ans. 441 C4H8(g) = CAH6(g) + 12(@) 1os780-— mmo BASIS: 1 mole C4H8 entering, of which 33% reacts. ‘The unreacted C4H8 und the diluent H2O pass throught the reactor unchanged, and need not be included in the energy balance. Thus 1 To 2= 298.15:K T= 798.15K 1 Evaluate AHy9g__ by Eq. (4.21): A 1: C4H6 2: H2 3: C4H8 2.734 26.786 8.882 0.0 3.249.) B=] 0.422 |-107? 0.0 |-107® D =} 0.083 |.10° 1.967 31.630 9.873 00 AA Yovd awe Pmw ae mc, AD Sad; AA = 4.016 AB =~4.422 107 aC = 991x107" pd = 83% 10° MDCPH(298.15,798.15 ,4.016,~4.422-10" 3,991.10" 7,0.083-105) = 1.94537 MDCPH := 1.94537 { ‘AHi29g + MDCPH-R-(T ~ To) Agog = 1.179 108 mol AH795 Q = 0.33molAH 7g QChapter 5 - Section A - Mathcad Solutions 5.2 Let the symbols Q and Work represent rates in kJ/s. Then by Eq. (5.8) [Work] [Qn] Te 98.15-K Qu = 250- Ans. By Eq. (5.1), Qe = [Qu] - [Work] 5.3 (a) Let symbols Q and Work represent rates in kJ/s Ty := 750K By Eq. (5.8): But (b) ny == 0.35 84 (a) Te := 303.15-K Ty = 623.15-K Te fee oe == 0.55-1Carot 20282 Ans. TH 7By Eq. (5.8), Tu * 5.7 Let the symbols represent rates where appropriate, Calculate mass rate of LNG evaporation: P= 1.0133-bar 198.15-K in PV molwt := 1722 miNG = —~-molwt mung = 62548 ‘mol RT s Maximum power is generated by a Carnot engine, for which [work] _ |Qr] - [Qc| [ee] [ee] Ty = 308.15-K Ca Qc = 512 -mpxo kg i (Ta Work = Qe] — Ans. (Te Qu = Qc + Work Ans.ASrorat = ASH20 + ASres is the same as in (a), and the total ivided into two halves. (b) The entropy change of the water heat transfer is the same, but (sche AStotal “= AS res + ASH20 (©) The reve -s an infinite number of heat reservoirs covering the range of temperatures from 273.15 to 373.15 K, each one exchanging an infinitesimal quantity of heat with the water and raising its temperature by a differen Ty = 500K Pv ns n= 1.443mol RT; (a) Const.-V heating; AU = Q+W=Q=n-Cy-(T)-T)) Tre Ti+ T= 1x 10K acy T) Po) By Eq. (6.18), $= tn| — | - Reta] ty Eq. (5.18), AS ofcr (®) nn(Z} ai cin 2) a8 = 20.7042 An Syn] = 1794 Ans. n-Cyln| ti AS: ! Mie ‘Whence PT) (b) The entropy change of the gas is the same as in (a). The entropy change of the surroundings is zero. Whence AStotal = 10. 794: 2 Ans. The stirring process is irreversible. 995.10 (a) The temperature drop of the second stream (B) in either case is the same as the temperature rise of the first stream Cp (A), ie, 120 degC. The exit temperature of the second stream is therefore 200 degC. In both cases we therefore have: (463.15) 463.15 473.15 Sq = Cptn| SO Sp = Cprln Ane Sas 15) a ie 8) Ans. (b) For both eases: AStotal ‘= AS + ASB Ans. (¢) In this case the final temperature of steam B is 80 degC, ie., there is a 10-degC driving force for heat transfer throughout the exchanger. Now co 463.15) in( 353 3) Pe 343.15 ) \ 473.15 Ans. AStotal “= ASq + ASB Ans. ag 5.16 By Eq. (5.8), AW = dQ= To Since dQ/T = dS, AW = dQ - To-dS Integration gives the required result. T= 400K To = 300K 582x100 mol 100J molK Th AS := Cp-In| — AS = ~11.799- T Work := Q—Tg:AS Ans. Qe = |Q| ~ [Work] Ans. Qo ASreservoir = = Ans. Te AS + ASreservoir Process is reversible, SAT Tyr := 600K = Tey := 300K = Tyg = 300K = Tea := 250K For the Carnot engine, use Eq. (5:8): Jw} _ Ty - Tea [Qui] Tar The Carnot refrigerator isa reverse Carnot engine. Jw] _ Ty2—Te2 ‘Combine Eqs. (5.8) & (5.7) to get: _— a (G-7) tog Jecsp Tez Equate the two work quantities and solve for the required ratio of the heat quantitic eee Tex fin=Te1) Tu (TH = Tee Ans, 7 S48(@) Ty = 300K Py L2bar Tp = 450K Pp = Ghar Cp == GR AH AS ©) onze ase 1.484 mol mol-K 101( aH= 3.8108 mol @ ane mol @ als 6651-1080 mal 5.19 The cycle is the same a identificaitons C=1; D= page 298: For the given data: 5 ( 973.15 - 473.15 7 (1973.15 — 773.15, J mokK J molK J mobK AS = 4.953, AS = 2.618 AS = -3.607 shown by Fig. 8.10 on page 298. With the ; A=3; and B=4, the efficiency is given by Eq. (A) on Work = 3.6x 10° mol Whenee Tp = T) + YOK ov AN 374K Ans. 102T= 800 Step 1-2: Volume decreases at constant P. Heat flows out of the system. Work is done on the system, Wioe {P(V2-vi)J= 4R-(12-T1)] Step 2-3: Isothermal compress out of the system. W: R-Ta-h = R-T2h ba) = R-Tyla| 2] = R-TyMa PruCaare (Po ley Step 3-1: Expansion process that produces work. Heat flows into the system. Since the PT product is constant, ‘Work is done on the system. Heat flows P-dT+T-dP = 0 (A) PVERT PdV + V-dP = R-dT PdV = R-dT- V-dP = RAT roe In combination with (A) this becomes PAV = RT + RdT = DRT Moreover, V1 -| Pave V3 Q5I = AUs1 — W31 = Cy-(T) - T3) #2-R-(T1 = Ts) Ws 2R-(T1- 13) = -2R(T1 -T2) Qi = (Cv+2R)(T1 Ts) = (Cp+R)(T1~T2) [Woe] _ [Wi2-+ Was + Wai] 1 Qa1 1 Cpe gR 1 = 700-K 350-K 403Py = LS-bar 3 J ={R(m2-1 Wiz = 2.91x 10 — Wr = {R(T -T1)] 2 = P3) 3_J Wo3 = R-Te in| > W3 = 2.017 10° — (Pi) mol 3] v31 = -2R(T) -T. Wai > -5.82x 10° — War = -2R(T1-T) 1 mal J Q31 = (Ce +R)-(T1-T) Q31 = 1.309 104 [Wiz + Was + Wai] @i 5.26 403.1SK Py 6.Sebar Tres =.298.15-K By Eq. (5.18), AS With the reversible work given by Eq. (3.26), we get for the actual W: (Po Work := 1.3-R-T-ln| =] (Isothermal compresion) Work = 4.163 10° — (Pt Q:=-Work Q here is with respect to the system. So for the heat reservoir, we have Ans, Ans, 5.27 (a) 10PS(473.15,1373.15,5.699,0.640.10"3,0.0,~1.015-10°) = 6448223 ICPS 448223, 104By Eq. (5.14) with P = const. and Eq. (5.15), we get for the entropy change of 10 moles 0-mo) AS = n-R-ICPS (by 10Ps(523.15,1473.15,1.213,28.78 ICPS := 20.234265 By Eq. (5.14) with P= const. and Eq, (5.15), we get for the entropy change of 12 moles 2-mol AS = n-RICPS 4s 5.28 (a) The final temperature for this process was found in Pb. 4.2a to be 1374.5 K. ‘The entropy change for 10 moles is then found as follows 0.0) = 10.835459 10PS (473.15, 1374.5, 1.424, 14394-1073, ~4,392-107 ICPS := 10.835459 nn s= 10-mol AS == mR-ICPS Ass 900 o> Ans, (b) The final temperature for this process was found in Pb. 4.2b to be 1413.8 K. ‘The entropy change for 15 moles is then found as follows: 630-107, -9.873-10" §,0.0) = 21.309212 eps(s33.15,1413.8, 1.967 ICPS := 21.309212 AS = 1 RCPS (c) The final temperature for this process was found in Pb. 4.2c to be 1202.9 K. ‘The entropy change for 18.14 kg moles is then found as follows icps(s33.15, 1202.9, 1.424,14.394-10" 3, ~4,392:107§,0.0) = 8.245741 ICPS := 8.245741 n:= 18140-mol AS = mRICPS aS= 4296x102 Am. 1055.29 The relative amounts of the two streams are determined by an energy balance. Since Q= W = 0, the enthalpy changes of the two streams must cancel. Take a basis of 1 mole of air entering, and let x = moles of chilled air. Then 1 - x= the moles of warm air. To = 298.15-K ‘Temperature of entering air Tr Tz x€p(Ty = To) + (1 =»)Cp-(T2-To) = 0 248.15-K ‘Temperature of chilled air 48.15-K ‘Temperature of warm air Given Thus x = 0.5, and the process produces equal amounts of chilled and warmed air. The only remaining question is whether the process violates the second law. On the basis of 1 mole of entering air, the total entropy change is as follows. Pp -bar 1; Ty AStotal = * con(Z) +(1=x)-Cp (2 \- nu) \To, 0) Po Ans. Since this is positive, there is no violation of the second law. 5.30 Ty := 523.15-K Cyi=Cp-R Q = AU - Work 108Q Q=-1.733% 10 ASpes “= ASres = 5.718 Tres mokK mol T Pp J pin] — | ~ R-ln} AS = -2.301 TT PL molK ASjoil = AS +AS;e —-“ASigg = 34=EE_ PROCESS IS POSSIBLE. mol 5.33 For the process of cooling the brine: pa aTi=-40K —— mdot:= 20-8 kek sec Ty := (273.15 + 25)-K Tr = 298.15K T2:= Q73IS-15-K Tz To = (273.15 +30)-K Ty = 303.15K Cp 258.15K I AH = -140— kg as = -0.501 2. kek Eq. (5.26): Wdotideal “= mdot (AH —Tg-AS) Wdotigeal = 256.938kW By Eq. (5.28): wjoy . dotideat mM Wdot.=951.6kW Ans. 534 E = 110-volt 9.7-amp Wdotmech != -1.25-hp Wdoteicct = FE Wdotetect = 1.067 x 10° W. At steady state: Qdot + Weoteject + Wdotmech = fu! =0 it Qdot +Sdotg = To dt 107Qdot := -Wdotetecr~ Wdotmech __ Qdot = -134.875W Ans, Sdowg O-amp = Ty = 300K Waotetect = 2.5% 10° W At steady state: Qdot + Wdoteleat = LU dt Qdot S +sdotg 5.38 mdot = 10——— Ty = (25+273.15)K Py 2= 10bar Ans. (©) Sdotg := mdot-AS (@) Ty = 20+273.15)K — Whost = To AS 1085.39(a) Ty = 500K Py == Gbar = Tz = 371K Pp s= 1.2bar To = 300K Basis: 1 mol AH = n-Cp(T2-T1) W,:= AH ‘Ans. 1s a(con(2)-n0() Eq.(527) —— Wideal = (AH = To-AS) Ans. Eq. (5.30) Wiost = |Wideal ~ Wsl Ans. Eq. (5.39) Ans. Ww, Widest Wise (a) -3753.8) ~5163) 1409.37 4, 8 (b) ~2460.93 -2953.91 493) 16432 (©) -3063.75 -4193.71 11300 a672 (a) -3853.5) 4952.4) 1098.8) 30632 (© -3055.45 4119.21 1063.81 3462 Py := 2500kPa Po = 150kPa To = 300K — mdot = 20! (P2) I = as ~Ren| = AS = 0.023. Py Sdotg = mdot-AS Waotiost *= 109$42 Quis IK) Wee 045K) Ty = (2504273.15)K Ty = 523.15K Te = (25+273.15)K = 208.15K Mactuat = 045 Nmax = 0.43 sv the process is impossible. Qi = 50K Ty = 350K Q@ T2 Ty = GIS +273.15)K Te 204273.15)-K Ty = 588.15K To = 293.15K Ans, Qdoty := LWeotl Qdote = Qdoty ~ [Waot] Qdote =:745.297MW (minimum value) | waot! (b) = 0.6-Nmax Qdoty, -= aot! Qdoty = 2.492 10° W n Qdote == Qdoty - |Weot} (MW (actual value) River temperature rise: Vdot := 165: 8 1 re oar eee Ans. emK Vdorp-Cp 11067 6.8 Chapter 6 - Section A - Mathcad Solutions At constant temperature Eqs. (6.25) and (6.26) can be written: dS = -B-V-dP and dH = (1 ~B-T)-v-dP For an estimate, assume properties independent of pressure. 1200-kPa 2095-10 2." ! Te = 408.1-K 28 emK gm om? mobwt + 58,1232 262.7. mol ‘mol Eq. (8.63) for volume of a saturated liquid may be used for the volume of a compressed liquid if the effect of pressure on fiquid volume is neglected. 359 088 | T T =| 360 /-K Tr Tr = | 0.882 | 361) fe (The elements are denoted by subscripts 1, 2, & 3 oF 131.601 2857 3 v =| vere 1] [ee Fiscal | mol (132.68 Assume that changes in T and V are negligible during throtling. Then Eq. (6.8) is integrated to yield: 1AH = T-AS4+V-AP but -vr(P2-Pi) Tr AH= 0 Then at 360K, AS el a We use the additional values of T and V to estimate the volume expansi 3 AV = V3-V, AV = 1.079. AT = 13-7, AT=2K mol -1.Av B = 4.098755 103K"! Vi AT Assuming properties independent of pressure, Eq, (6.29) may be integrated to give AS = cet BV-AP AP :=Po-Py AP = -2x 10°kPa Ty (a8 +8-VraP) Whence t= 10S +B-¥r AP) TORK Ans. Cp molwt : 69 T= 208.15-K Pj = Lbar Pp = 1500bar 3 250-107 87! bar”? Vip = 1003 kg em? By Eq. (3.5), Vo := Vyexp[-1-(P2~Pi)] Va = 937. 54 : 8 Vi tV. 7 Vave "= = Vave = 970.2875 By Eqs. (6.28) & (6.29), AH = Vave-(1- B-T)-(P2- Pi) AU := AH ~(P2-V2~ PV) B AU 8 ns. ke Qs TAS Work := AU-Q 1126.10 For a constant-volume change, by Eq. (3.5), f(T2-T1)—K-(P2—P))= 0 Ty = 298.15-K Ta: 323.15-K 1 Py bar = 442-10" °-bat™ 36.210 °K"! Ans. 6.14 --- 6.16 Vectors containing T, P, Te, Pe, and @ for Parts (a) through (n): 300 40 308.3 61.39 (187) 115 15 150.9 48.98 000 | 575 30 562.2 48.98 210 500 50 425.1 37.96 200 325 60 304.2 73.83 24 175 60 132.9 34.99 048 piel? lag pel? tour tere | 2954 {5 oar vc 18 650 30 553.6 40.73 210 300 35 282.3 50.40 087 400 70 373.5 89.63 094 150 50 1262 34.00 038 575 Is 568.7 24.90 400 375 25 369.8 42.48 152 475, 75. 365.6 46.65, 140) ? > P eee Pras 113,6.14 Redlich/Kwong equation: © := 0.08664 := 0.42748 -_ Bs {e 2) (3.50) ‘Guess: z=l Give ~ 4B 3.49) Given 1+B-aB oy G49 2(B,q) = Find(z) ( Gs fs hl4 k in{ 206i) +B: (6.62b) \Zl6:.a) 1)-1.5-qi]] (6.64) The derivative in these T3{(2( SR; = R-(in(Z(B;,q))) —fi—0.5-qr) (6.65) equations equals -0.5 FRy SRi 2.302103) 76.218) “poee108} mol [7.976] SSit03 Ans. 1166.15 Soave/Redlich/Kwong equation: = 008664 = Ye oarTas c= (0.4804 15740-01760") aeeaseeeae saa es os\P Pr wa (1 —Tr = — (3.50) — (3.51, a=[ireG-n)P pe (2% G50) 4 (4) Bsn Guess: z Given 2=1+P-q8-—~—2, B49) 2(B,q) := Find(2) 2(2+B) os t ‘The derivative in the following equations equals: (2) ai i= of Zoe 2\Bi ai HR; = RR: nal.) -1 [a (=y" + | wleso a x|w2.a)-01-a() “w| (6.65) CF isl.l4 } (6.62b)i (0.37464 + 1.542260 ~ 0269020?) 6.16 Peng/Robinson equation: ¢ := 1+/2 2 = 0.07779 Y= 0.45724 c pee eeAeeee 2 2 os’ Pr ea) veLi+e(-Te ={2-—]| G50) q:=|——| 651) ai-[i+el )| B ( *) 4 (2 < Guess: 2 z-B iz Gi Fl+p— 7———— (349) Z(B,q) := Find ven 8-98 Caieren) (B.q) := Find(z) (tr )\°> ‘The derivative in the following equations equals: sale ai) 2(Bi,ai) + 0-Bi) be tald tin Lo 2b) +0 (6.62b) 2Y2 \Z(Bi.ai) +e-Bi HR =n 0.9 ot (6.64) ] | (6.65) tas 103 “mol 38.054) miolK “3.861103 |: 2505-109] 2.EB5-103 a e 768 109 435105] | ae Bia 103 “877103 208 109 ABSA} AS57108} * 3 2103] 3.947.403 55:78} 116Lee/Kesler Correlation — By linear interpolation in Tables E. HR)? car)! HR hO equals ~ hI equals = h equals 0 ety 0 equals a sl equals “ s equals & 686 093 950 1.003 590 ASS =1.709 A471 778 024 ~705 675 ons -1319 ms 008 993 744 165 =1.265 108 =019 962 699 ao | | -1200 710 ~.001 ~.770 742 007 =875 651 a4 1.466 167 =.034 = 73 716 032 ~701 746. «154 1.216 Z:=(Z0+o21) B54) h(h0+ohl) 676 UR: 11771 =961 1.10 ~492 -497 ~.549 =.829 -A43 -631 ~.590 -110 ~296 -.674 ~.700 eee 50:5 (S0+os1) SR ~750 441 517 509 587 555 97 -429 ~sil 589 ~491 =.563, =.688 ~287 216.107 - * [aaaas08 O78) SpE ‘01689 ‘A.87403) aver) Be 0.752] 21.407;103| [0.707 4 or 6.952:103) nT) H1.G2- 105} 0748) 2.802103] ose) Fas 708 0765} Az] ores BRED 0.768 | 53786:103| 118617 :23.15-K, ts ‘The pressure is the vapor pressure given by the Antoine equation: (50) = 36.166 2788.51 + 220.79, PY) eo(s 8858 — Spa = 1375 6.166KPa Pd = 1375-828 dt K (a) The entropy change of vaporization is equal to the latent heat divided by the temperature, For the Clapeyron equation, Eq. (6.69), we need the volume change of vaporization. For this we estimate the liquid volume by Eq. (3.63) and the vapor volume by the generalized virial correlat For benzene: Pe = 48.98-bar Zoi 0.271 P Pris Pr = 0.007 P Bo = -0.941 Bi = 139 — 2172 By = -1.621 a2 Tr Voap = 7.306 x 10° mol 02887 3 -n) By Eq. (8.63), Viig = veal! ed Vig = 93.15 mol Solve Eq. (6.69) for the latent heat and divide by T to get the entropy change of vaporization: AS := dPdt-(Vvap- Viig) Ans. (b) Here for the entropy change of vaporizati R-T AS = 7 dPdt Ans. 1196.20. The process may be assumed to occur adiabatically and at constant Pressure. It is therefore isenthalpic, and may for calculational purposes he considered to occur in two steps: (1) Heating of the water from -6 degC to the final equilibrium temperature of 0 degC, (2) Freezing of a fraction x of the water at the equilibrium T. Enthalpy changes for these two steps stim to zero: Cp-At +-AHfsion = 0 The entropy change for the two steps is: Ty = 273.15-K Ty = (273.15 - 6)-K (T- x-AH, nm cptn{ 22), XA Hfison TT T2 The freezing process itself is irreversible, because it does not occur at the equilibrium temperature of 0 degC. 6.21 Data, Table F. 1156,3- Bry Ho = 1533.4 BYU Ibm Ibm TT $1 := 1.7320BMU_ g, BM. lbmrrankine lbp AH := H- Hy AS = ate + te He Fei Ans. For steam as an ideal gas, apply Eqs. (4.9) and (5.18). [t in degF] ty = 227.96 t= 1000 Py := 20psi Pp = S0-psi 21 . Eee eeer a 7 ty, 2382017 The ee 87 1, = 10.9028 (ketvins) (kelvins) 120Mecpui(382.017,810.928,3.470, 1.450-10"3,0.0,0.121-108) = 4.373944 Mcps(382.017,810.928,3.470, 1.450-10"%,0.0,0.121-10°) 1339091 MCPH := 4.373944 MCPS := 4.339091 molwt := 18. b Ibmol R-MCPH: wnkii AH = (2-4) rankine BTU ans, molwt ( (T2 Po) Be MePsnl ~ bl oii ences 1 eeaEAE I molwt 6.22 Data, Table F.2 at 8000 kPa: Viig = 1.384 Fig = 1317.1 Stig = 3.2076 gm gm amK om? J J Veap = 23.525 Hyg = 2759. Syap i= 5.74712 gm gm-K 15-108 5 em mig = ————— myap ‘= — Mig Hott = mig Hig + Map Hyap Stotal = Mig: Stig + Mvap'Svap 1246.23 Data, Table F.2 at 1000 kPa: Viig 6.24 Data, Table F.3 at 350 degF: 3 Vig := 0.01799. Ibn Hig = 321.762 Mig + Map = 3-Ibm 3.1m mig = ——"— 30-Vji 1+ Vvap Map '= 3-lbm— Mig Heal = Mig’ Hig + ™ap"Hyap Hiotal I Sig 2.1382 3 f Voap = 3.342-—— ‘vep bp BTU Hyap = 1192.3-—— ae Ibm S0-miig Vig _ Map: Wap = 50-mig:Viig Mig +? = 3g ap Imig = 2.36410 yap = 0.63616 =15191BTU Ans. 1226.26 Data, Table F.1 at 230 degC: 90.3 Siig #= 2.6102. em gm-K (1 = ¥)Hig +x Fyap xe 0582 Aas. Viotal = miotal: Viig + Myap'AV|y pe) Table F.l, em Viotal °= 0.15 130 degC: Vvap >= 392.4- a 3 Table F.l, om 30 degC: AV iy = 32930- Veotal Veotal ~ Motat Vi Meal = 2 Mygp = 2 Mota Vita wap AV Moral = 0.382kg Myap = 4.543 x 10° ?kg Mlig ?= Mrotal ~ Myep Ans. 1236.27 Table F.2, 1100 kPa: Interpolate @101.325 kPa & 105 degC: Const.-H throttling: Hy 5 Huig + %+(Hyap - Htiq) H - Hig Fivap = Hig XS 01953 Ans. 6.28 Data, Table F.2 at 2100 kPa and 260 degC, by interpolation: 2235-2. 81 = 6.5640 motwt := 18.0152 Hy gm emK mol Hy == 2923.5 Final state is at this enthalpy and a pressure of 125, em kPa. By interpolation at these conditions, the final temperature is 224.80 degC and 7.93162 AS := 82-8} 58 3 mk = emk For steam as an ideal gas, there would be no temperature change and the entropy change would be given by: Py = 2100-kPa Pp = 125-KPa 6.29 Data, Table F.4 at 300(psia) and 500 degF: Hy = 1257.7. BTU 3703. B TU lb Ibpytankine BIU ; oe Hp := 1257.1. Final state is at this enthalpy and a pressure of Thm 20(psia). By interpolation at these conditions, the final temperature is 438.87 degF and BIU BTU 8606-———_. = S)- 7 oe AS :=S2~S; AS = 0.29 Ses Igy tankine 1246.30 631 For steam as an ideal gas, there would be no temperature change and the entropy change would be given by: Ib Py = 300- molwt := 18- a Ibmol P -R o( 2) oe 1) Ans. molwt Data, Table F.2 at 500 kPa and 300 degC Sy := 7.4614- 4 Phe final state is at this entropy and a pressure of gm 50 kPa. This is a state of wet steam, for whi Stig = 0912-4 Svap = 1.5947. mK mK i Hig *= 340.564— gm S2= $1 = Stig +%-(Svap ~ Stig) x= 058 Ho = Hig + X-(Hyap ~ Mig) ‘Ans, Vapor pressures of water from Table F.1: At 25 degC: Pat 2= 3.166:kPa P= 101.33KPa — Xwater != At 50 degC: Psat Psat : vater = Riyater 05122" Ans. 1256.32 Process occurs at constant total volume: Vaotal “= (0.014 + 0.021)-m? mass ‘= Mig + Myap x= 4158x104 (initial quality) _ Veotal ee cm? This state is first reached as 2 Tass i" gm Saturated liquid at 349.83 degC For this state, P = 16,500.1 kPa, and I J U; 1641.7-— Uy = Ulig + X(U yap — Unie Uy = 419.868 — a 1 Ulig+%(Uvap ~ Utig) = Qs U2-Ur Ans. 3 6.33 Veotat := 0.25mi Data, Table F.2, sat. vapor at 1500 kPa: 3 Vj = 131.66 U) = 2592.4 gm Of this total mass, 25% condenses making the quality 0.75 x = 0.75 Since the total volume and mass don't change, we have for the final state: Vo = Vi = Viig +x-(Vvap— Vig) ‘Whence: Vi~ Vtig : 5 : x= +4 (A)__Find P for whieh (A) yields the value x = 0.75 Vvap- Vig for wet steam 1266.34 Since the liquid volume is much smaller than the vapor volume, we make a preliminary caleulation to estimate: af ag iz Voap = 175.547 Yvan. ‘This value occurs at a pressure a bit above 1100 kPa. Evaluate x at 1100 and 1150 kPa by (A). Interpolate on x to find P = 1114.5 kPa and J Utig += 782.41 ale Uyap *=.2584.9-— gm am ii = Uti yap ~ UI Uz = 21343— Up = Utig + (Uvap Urig) 2 a Q = mass-(U2- Ui) QE=869.9kI Ans. 3 Table F.2,101,325 kPa: Vyap = 1673.0 ‘am Urq = 418.959-— Uyap #= 25065: ig 418.959 nap = 25085 198m? yap = otal = Mig + Map Vvap Vi = Vig + (Wvap~ Vtig) Vi = 98.326 Ur = Ulig+ ¥-(Uvap~ Uti), = 540.421 ee Since the total volume and the total mass do not change during the process, the initial and final specific volumes are the same. ‘The final state is therefore the state for which the specific volume of saturated vapor is 98.326 cu em/gm. By interpolation in Table F.1, we find t= 213.0 degC and 1276.35 6.36 Data, Table F.2 at 800 kPa und 350 degC: em? 3 3 Vy = 354,34 Uy == 2878.9-— Voota #= 0-4! ‘em. =m The final state at 200 degC has the same specific volume as the initial state, and this occurs for superheated steam at a pressure between 575 and 600 kPa. By interpolation, we find P = $96.4 kPa and J Veotal Ug '= 2638.7-— U2 -U Ans. a aoa 2 2 (u-u) Data, Table F.2 at 800 kPa and 200 degC: Uy = 2629.9 51 = 68148—— gm gmk (a) Isothermal expansion to 150 kPa and 200 degC Ups 2656.3 So = 7.6430 am emK Q = mass-T-(S)~$)) Q=30220K Ans. Also: Work := mass-(Uz—U})-Q (b) Constant-entropy expansion to 150 kPa. The final state is wet steam: 729345 gmk Svap 3 Uyap = 2513.4 = 0.929 Uhiq + % (ap ~ Utig) Wis m(U2-Uy) W= 262527 ig Ans. 1286.37 Data, Table F.2 at 2000 kPa: 6.38 x12 0.94 Hig 2= 908.589-—— gm ‘i ad Hy = Hig + -(Hyvap- tig) Hi = 2.684 10° — mass := I-kg am For superheated vapor at 2000 kPa and 575 degC, by interpolati Q := mass-(H2- Hy) ‘Ans, First step: Qi2=0 Second step: W235 0 For process: Q=U3-Un Table F.2, U, = 2601.8: z Wap = 2601.82 2700 KP: gm xp = 0.9 Table F.2, 400 kPa: Svap = 6.2244) gmk Up = Utig + 1-(Uvap — Unig) Uy = 2.439% 109. em 3 mi 81 := Siig + X1-(Svap- Stig) Sy = 5.861 x 10 a Stig = 1.7764 ‘K Uyap = 2552.7. am 3 Vvap 2= 462,22. gm 129Since step 1 is isentropic, $1 ~ Stig So = $1 = Stiq + ¥2-(Svap ~ Stiq) a x = 0.798 'vap ~ Stig ee Ua := Utiq + x2-(Uvap ~ Uliq Uz = 2.159 10° — gm f om? Vo = Viiq + x2"(Vvap— Vig) Vp = 369.135— gm V2 __ and the final state is sat. vapor with this specific volume. Interpolate to find that this V occurs at T = 509.23 degC and U3 = 2560.7 Whence Q::= U3-Up Work := U2 Uy Ans. J 6.39 Table F.2, 400 kPa & Si = 7.0548-—— 175 degC: gm: Table F.1.sat. vapor, J ‘Sq = 6.6221-—— 175 degC 2 mk mass := 4-kg T r= (175 +. 273.15)K Q = mass-T-(S2- $1) W = mass-(U2-Us)-Q Q=-775.66k] Ams. = W=66766k] Ans. 6.40 (a) Table F.2, 3000 kPa and 450 degC: Hy = 3344.6 si = 7.0854 gm gm-K Table F.2, interpolate 235 kPa and 140 degC: J Hp = 2744.5.— Sp i= 7.2003 130Ans. Tp w= (140-4 273.15)-K Ty = 413.15K = 235-kPa i 3 = tcpal(723.15,413.15,3.470,1 450-1079, 0.0,0.121-10°) = -1343.638 ices(723, 15,413.15, 3.470, 1, 450-107? 0. 0,0.121 10°) 2.415901 ICPH := -1343.638-K ICPS := -2.415901 Eqs. (6.86) & (6.87) for an ideal gas: molwt = et P)) R, ICPS - (| As, Vu baie molwt Ans, Ta = 1.11752 Pry = 0.13602 Tr = 0.63846 Pz = 0.01066 ‘The generalized virial-coefficient correlation is suitable here HIRB(1.11752,0.13602,0.345) = -0.13341 HRB, := ~0.13341 SRB(1.11752,0.13602,0.345) = -0.08779 SRB; := -0.08779 HRB (0.63846 , 0.01066, 0.345) = -0.04422 HRB2 == ~0.04422 ‘SRB(0.63846 ,0.01066,,0.345) = -0.05048 SRB2 := ~0.05048 131641 Data, Table F.2 superheated steam at 550 kPa and 200 degC: 7.0108 2640.62 gmK gm. Up i= 2963. pb Soe 757922 Qi2 = U2=Uj) gm gmK Qn = 32252 Step 2-3: Isentropic expansion to initial T. gm : I Qo3 = 0 835 7.5782——— em-K ‘Step 3--1: Constant-T compression to initial P. T= 4BASK Q3) = T(S- $3) For the cycle, the internal energy change ~0. —Weycle n Qi Ans. 642 Table F.4, sat.vapor, 300(psi): Ty = (417.35 + 459.67)-tankine Hy i295 mn Ty = 877.02rankine 1= 1.51052 ibprrankine 432Superheated steam at 300(psi) & 900 degk BIU BTU. = Sates 1,7591- Hy = 1473.6- Tm 2 Bar ine BTU Qi2:= Ho-Hi Q31 = Ti(81~- $3) Qs = -218.0075— For the cyele, the internal energy change = Woyele = —Qeycle = ~Q12~ Q31 Q31 neste Qi2 6.43 Data, Table F.2, superheated steam at 4000 kPa and 400 degC: 81: 67733-— For both parts of the problem: gm (a) So we are looking for the pressure at which saturated vapor has the given entropy. This occurs at a pressure just below 575 kPa. By interpolation, 572. Ans, ees (b) For the wet vapor the entropy is given by x= 095 S2= Stig + X-(Syap~ Stig) So we must find the presure for which this equation is satisfied. This occurs at a pressure just above 250 kPa. At 250 kPa: J J son Svap = 7.0520: Stiq S2= Stig + x-(Svap ~ Stig) So = 6.77982 Slightly > 6.7733 gm-K By interpolation Boy 1336.44 (a) Table F.2 at the final conditions of saturated vapor at 50 kPa: ky Sp = 7.5947 — 1 = 2646.0 S122 kek ke Find the temperature of superheated vapor at 2000 kPa with this entropy. It occurs between 550 and 600 degC. By interpolation Ko 4 59.16 (degC) Hy = 3598.0-— kg Superheat: At = (359,16 ~ 212.37)-K. kg (b) mdot = Wot := |mdot-(H2-H1)| 6.45 Table F.2 for superheated vapor at the initial conditions, 1350 kPa and 375 degC, and for the final condition of sat. vapor at 10 kPa: kJ kK kd 205.4 $1 = 7.2410-— Hy := 2584.8-— kg kgK kg If the turbine were to operate isentropically, the final entropy would be S2= 8) Hy Table F.2 for sat. liquid and vapor at 10 kPa: ky Shiq :=:0.6493-—_ kgK Mig := 191.832 = Hyap '= 2584.8 S2- Stig x Ban Sue x2 = 0.879 H = Hig + X2-(Hyap — Hig) H=2294x 10° kg ay = 0.681 Ans. 1346.46 Table F.2 for superheated vapor at the initial conditions, 1300 kPa and 400 degC, and for the final condition of 40 kPa and 100 degt aas0.7-0 s) = 73404 Hy = 2683.82 kg kg-K kg If the turbine were to operate isentropically, the final entropy would be H Hy Table F.2 for sat. liquid and vapor at 40 kPa: kD KD Stig = 1.0261-—— Syap = 7.6709-—— ‘a kek pT OO Ky Ky Hig = 317.16-— Hyap = 2636.9-— kg kg S2- Stig Ses Sha x2 = 0.95 Hyiq + x2-(Hyap - Htig) Ws 2.522% 198 32.85- H = 2856.3 gm. gm Table F.2 (ideal-gas values, 1 kPa and 225 degC) J 10.0681-—— Py = 1-kPa. em! T = (225 +.273.15)-K 498.15K vei-v-_1 molwt P ‘The enthalpy of an ideal gas is independent of pressure, but the entropy DOES depend on P: Hp = H-Hig 1356.48 @ = 0345 Pe T, + = 0.76982 Pret P, = 0.072546 Te Po ‘The generalized virial-coefficient correlation is suitable here . 0.172 By = 0.083- 2822 ay =-0.558 By = 0.139- By = -0377 16 a2 T T By Eqs. (3.58) & (3.59) along with Eq. (6.40) Pr RT Z = 1+(Bp+@-By)-— Z=0,935 Veo Z-1 (Bo+ oi} z R* Bmowwt HRB (0.76982,0.072546 ,0.345 ~0.178580 HRB := -0.178580 SRB(0.76982,0.072546,0.345) = -0.167101 SRB := ~0.167101 T= (179.884273.15)K oT (Table F.2) molwt := 18.015 2% mol om? em? Vy 1.127 194,29. AViy =v gm J Hy := 762.605-— AHy = Hy - Hy am Aly = Sy~ S) 1363 AVyy = 193.1639 AH = 2.014107. ag, = 4.445 em em gmK (@) Gy: Hi TS) 6 =-206.062. Gy = Hy TSy Gy = 206.01 gm gm J i (b) AS, = 4.445 —— 4.445 —— amK em-K © Vrs Ans. For enthalpy and entropy, assume that steam at 179.88 degC and 1 kPa is an ideal gas. By interpolation in Table F.2 at 1 kPa: Hig = 2841. p= 9.8834 em emK kPa The enthalpy of an ideal gas is independent of pressure; the entropy DOES depend on P: (@) Assume In P vs. 1/T linear and fit three data pts @ 975, 1000, & 1050 kPa. 975 178.79 Data: pp := | 1000 |-kPa 179.88.) (degC) i= 1.3 1050 182,02 1 iy n( 2) Slope = slope(x,y) Slope = -4717 4273.15 (kPa) ae ‘Slope-K dPdT 22.9848 pdt 437AVjy-dPdT. Reduced conditions: « := 0.345 0.7001 The generalized virial-coefficient correlation is suitable here o4 0172 Bo = 0.083- 2972 y= -0664 By = 0130-842 By = 063 16 42 Tr T, By Kgs. (3.58) & (3.59) along with Eq. (6.40) Pr R-T Z:=1+(Bo+o-B1) Z=098 VR = ———(Z-1) es P-molwt HRB(O.7001 0.0453 0.345) = ~0.1444 ‘SRB(0.7001 ,0.0453,0.345) = -0.1493 RT. HR = molwt 6.49 Ts (358.43 + 459.67)-rankine T = 818.Jrankine (Table F.4) BTU Ibprrankine S1:= 0.5141ae BTU AVy = 2.996-— AHy = 863.45—— Ibn Ibm @) G:=H|-T-S) Gy = Hy-TSy Bru Gy = -89.94 BTU SH (b)aSjy = 1.055——__ Ibprrankine T RI © Va W- iz . molwt P bia For enthalpy and entropy, assume that steam at 358.43 degF and 1 psi is an ideal gas. By interpolation in Table F.4 at 1 psi: 1222.6 Sig 21497 pgs Ibn Ibyetankine Hi psi ‘The enthalpy of an ideal gas is independent of pressure; the entropy DOES depend on P: Hp = Hy ~Hig Ans. BIU Ibrrankine (d) Assume In P vs. 1/T linear and fit threedata points (@ 145, 150, & 155 psia) 14s 355.77 Data: pp:=/ 150 |-psi_ t= | 358.43) degF) 1.3 155, 361.02 139Slope ‘= slope(x.y) Slope = -8.501 x 10° aPaT == —-Stope-rankine dPdT = 1.905 2 rankine este on eee og Spy = AV)-dPdT Siy = 1.056: i Ans. ASiy = AViy AS = (000 Pos 220.55-bar T T, = 0.7024 P, = 0.0469 Tr ‘The generalized virial-coefficient correlation is suitable here 0.422 0.172 Bo = 0.083-——— By = -0.65 By = 0.139-——= By = -0.62 1,6 782 By Eqs. (3.58) & (3.59) along with Eq. (6.40) Pr RT Z=1+(Bp+oB)— 72-0982 Z- Boros R= Bimota 7D FIRB (0.7024, 0.0469,0.345) = -0.1482 HRB := ~0.1482 SRB(0.7024 0.0469 0.345) = -0,1526 SRB == -0.1526 1406.50 For propane: Te 69.8-K Po i= 42.48-bar 0.152 T= (195 +273.15)-K T= 468.15K P= 135-bar T Pp = = 3.178 To Pe Use the Lee/Kesler correlation; by interpolation, 639 0.6141 Zy:= 01636 Z = Zt oLy Ans. Hay = ~0586-R-Ty Higo = ~7.674« 10° Hy = -1.802% 10? 2 mol ‘mol Spo = -1463-R Sai = -O.717-R l Spo = -12.163. Spt = 5.961 aa molK ey molK Hp = Hgo + o-Hpy Sa = Sro-+o-Se1 3 J Hp = -7.948 10° Sp = -13.069 ee mol . molK 07 3,-8,824-10" 0.0) = 1766.023 1cPH{308.15, 468.15, 1.213,28.785 1ops(308.15,468.15, 1213,28.785-10"°, -8.824-107 6,0.0) = 4.56487 ICPH := 1766.023-K ICPS = 4.56487 AH := RCPH + HR Ans. As Ans. {ices - «(F)) +8R 1416.51 6.52 369.8K Pos 42.48-bar ew = 0.152 For propane: Te T=343.1SK Pg := 101.33-kPa P 500-kPa, T= (10+273.15)-K Tet T, = 0.92793 Te P, = 0.35311 ‘Assume propane an ideal gas at the initial conditions. Use generalized virial correlation at final conditions. HRB(0.92793 0.35311 0.152) = 0.465534 HRB := ~0.465534 SRB(0.92793 ,0.35311,0.152) = —0.346693 SRB 0.346693 AH := R-Te HRB Ans, {se uf - ) ge 4S = R+| SRB— In| fe Ans. (Po) AS 5 OT oR a For propane: 0.152 Tei 36.8K 42.48-bar 200.0. mol If the final state is a two-phase mixture, it must exist at its saturation temperature at 1 bar. This temperature is found from the vapor pressure equation P= |-bar A := 6.72219 B = 1.33236 2.13868 Dis 1.38551 x(T) r Guess: T= 200-K Given 7 =P, onl 220 +B(n)!S +c) +D-4cD)*] E 1-1) | Find(T) T = 230.703K The latent heat of vaporization at the final conditions will be needed for an energy balance. It is found by the Clapeyron equation. We proceed exactly as in Pb. 6.17. 142onl +(1) +B-(1(1D)'* + €-(2¢)§ +d. (cn)*] >) 1-1(T) T = 230.703-K 4 pry = 44g hPa dPdT 4.428124. 428 aT K K P Pree Py = 0.024 Ty Tr = 0.624 0.422 Bo := 0.083 — Bo =-0.815 By = 0.139 16 Tr RT Pr Vvap a) +(Bo+o-Bi) . Vig om 3 Viap = 1.847% 1045 Viig = 75.5452 mol Abliy := T-(Vvap ~ Viig)-4PaT Ay = 1.879 we imo ENERGY BALANCE: For the throttling process there is no enthalpy change. The calculational path from the initial state to the final is made Up of the following steps: (1) Transform the initial gas into an i (2) Carry out the temperature and pressure changes to the final T & Pin the ideal-gas state. (3) Transform the ideal gas into a real gas at the final T & P. (4) Partially condense the gas at the final T & P. ‘The sum of the enthalpy changes for these steps is set equal to zero, and the resulting equation is solved for the fraction of the stream that is liquid. For Step (1), use the generalized correlation of Tables E.7 & E.8, and let 0 1 -(2) aa pace OF RT. 1 Rh 143Pe P, = 4.708 Pe 1 = -3.773 1 = 3.568 J : at By Eq. (6.76) AH; Te (ro + 11-0) AH, = 1.327x 10° — mol For Step (2) the enthalpy change is given by Eq. (6.86), for which 3 icpHi(370, 230.703, 1.213,28.785-10 3, -8.824-10" 0.0) = -1260.405-K AH := R-(-1260.405-K) AH) = - 1.048 « wie mol For Step (3) the enthalpy change is given by Eq. (6.78), for which 703 tye BUR ona HIRB (0.6239, 0.0235 ,0.152) = P, = 0.0235 0.07555, 0.07555, AHg := R-T- HRB For Step (4), AHy = -x-AHyy J ‘AH = -232.28—— mol For the process, AH) + AHg + AH ~ x-AHy = ‘AH, + AH + AH3 AHyy 136° Ans. 653 For 1,3-butadiene: @ := 0.190 425.2-K 3 Po: 42.77-bar 267 20.4 Ty = 268.7-K mol T= 380K 1919.4-kPa 27B1S-K Po = 101.33-kPa = 0894 P P, = 0.449 Pe 144Use Lee/Kesler correlation, HOWEVER, the values for a saturated vapor lie on the very edge of the vapor region, and some adjacent numbers are for the liquid phase. These must NOT be used for interpolation. Rather, EXTRAPOLATIONS must be made from the vapor side. There may be some choice in how this is done, but the following values are as good as any: Zo: Z=0718 7442 Ze ZRT P Vvap Hpo i= -0.689-R-Te Heo = ~2.436% 10° mol Spo = -0.540R J i Spo =—4.49 Spi = 7.383 RO mokK RI molK Hro+@HrRt Sr == Spo + @-SRi J Sp = -3.892 x molK 1cPH(273.15,380,2.734,26 786-10" >, -8.882-10" 60.0) = 1124.694 0) 3.45478 ICPH := 1124.694.K ICPS := 3.45478 icps(273.15,380,2.734,26.786-10">,-8,882.10" 6, Hyap = RICPH + HR Svap := R- [reps - o(F)) +SR Po}) 145,For saturated vapor, by Eqs. (3.63) & (4.12) {a-1)87] 3 cm jeZet 7 om Ans. Viiq = VeZe Mia 5 10088 rol AG (®)-195) 7) ’ enna OM Se AH, = 22449— AH, = R-Ta! To \ mol 930 - Tea r 0032 By Eq. (4.13) = AHy| — AH = 14003 Hiig = Hyvap ~ A Aus. cas Ans. Stiq = Svap ~ st ig = Svan 6.54 For n-butane: 37.96bar Ze = 0.274 Ty t= 272.7-K 70K 1435-kPa Po = 101.33kPa Tr, T. = 087 0.378 Te Use Lee/Kesler correlation. HOWEVER, the values for a saturated vapor on the very edge of the vapor region, and some adjacent numbers are for the liquid phase. These must NOT be used for interpolation. Rather, EXTRAPOLATIONS must be made from the vapor side, There may be some choice in how this is done, but the following values are as good as any 146J 2.733% 10° — Hr = mol 1epH(273.15,370, 1.935,36.915-107* reps(273.15,370,1.935,36.915-10" ICPH := 1222.048-K § -11.402-10 Z= 0742 ZLakoroLy Hpy := -0.83-R-Te Her = -2.937 10° mol Spi = -0.835-R Sri = -6.942 dau mol K SR = Spo +@-SRi J Sp = -5.421 morK 11,402.107,0.0) = 122.088 $0.0) = 3.80735 3.80735 ICPS ») (P Svap := R-| ICPS — In| ae ) +Sz (Po, [(r-90*7 Viiq= VeZe ( (P. \ 1.092,{ in ©] — 1.013 AH, = R-To peieseh SERS etna . 0.930-—* Te 147 AH, = 22514 | aot | = mol038 ast = 152952. mol By Eq. (4.13) AH Hig = Hyap ~ AH Ans, AH Sig == Svan * Ans. 6.55 (a) The final-state volume of acetylene is (750~33:5)-em? Vegas = 58Sem> T= 398.15-K = 0.187 3083K Pe = 61.39-bar T= 1291 Guess: Zi 0.65 P P = 183.9bar Py = BR Py = 2.996 Pressure is clearly high, and requires use of Lee/Kesler correlation. Solution is by trial, because P is unknown but is required to find Z. Start with reduced pressure from guess value above. The eventual result for a reduced pressure of 3.07 is: Zo := 0.6298 Zy = 0.1948 Zo traZy, Z = 0,666 Z0R-T oe a p= ot Peis P, = 3.07 188.5bar Ans. Ves Pe () By the first law, Q = n-AU = n-(AH — A(PV)) Q= n(4H-V-AP) = n-AH ~ Veag-AP The enthalpy change is evaluated by a three-step process: (1) Reaction at 298.15 K (2) Change in T for products in std. states @) Transformation to state of real gas From these, 148AH = AH9g + AHp + H® Step (1): From data of Table C.4 AH p9g ‘= [ -986090 + 227480 - (~59800) ~ 2-(~285830) } oat mol J 127180 — mol Step (2), Table C.1 data, for acetylene(g): McPH(298.15,398.15,6.132, 1.952-1073,0.0,-1.299.105) = 5.71731 Table C.2, for caleium hydroxide(s): McPHt(298,15,398.15,9.597, 5.43510 AH} 98 = 0.0,0.0) = 11.48920 For the products, MCPH := R-(5.71731 + 1148920) MCPH = 143.055. motK AHp := MCPH-100-K AHp = 143055 mol Step (3), from Tables E.7 & E.8 at the reduced conditions of Part (a) for acetylene: Hpo = -2.340-R-Te Ai = -0.384-R-Te Fro = -3.998% 10° 2. Bar = -984.271 mol mol Hp = Hro + @-HR1 AH := AHagg + AHp + Hg Q = MAH ~ Vgas(P ~ I-bar) 6.56 Propylene: @ := 0.140 400.15-K P= 38:bar Po: I-barThe throttling process, occurring at constant enthalpy, may be split into two steps: (@) Transform into an ideal gas at the initial conditions, evaluating property changes from a generalized correlation. (2) Change T and P in the ideal-gas state to the final conditions, evaluating property changes by equations for an ideal gas. Property changes for the two steps sum to the property change for the process. For the initial conditions: T P as Ty = 1.095 Pes Py = 0815 Te. : Pe Tre Hp := Ho + @-Hy Hy = -1.623« 85x10 mol S] = -0.496-R Sr = So+o-S} J 0 = 4.697 $y = 4.124! mol-K molK Step (2): For the heat capacity of propylene, 22.706-10" K Solve energy balance for final T. See Fq, (4.7). Acs 1637 B t=1 (guess) Given H=R (fa vee 2ar(e— )] + £ P(e. | t= Find(z) .908 Tit T286327K Ans. Icps' (400 15,363.27, 1.637,22.706-10" ~ 6.91510 0.0) 0.898338 Ices ).898338 Po ASig = n{tces ae (3) ASjg = 22.774: 2 \P ig mol K 1506.57 The throttling process, occurring at constant enthalpy, may be split into two steps: (1) Transform into an ideal gas at the initial conditions, evaluating property changes from a generalized correlation. (2) Change T and P in the ideal-gas state to the final conditions, evaluating property changes by equations for an ideal gas. Property changes for the two steps sum to the property change for the process. For the initial conditions: a Ty = 1.144 Pee Pr = 0.518 Te Po Step (1): Use the generalized virial correlation Tr HRB(1.14386, 0.51789, 0.152) = -0.444283 SRB(1.14386,0.51789,0.152) Hg := R-TeHRB Hp = -1.366% 10° mol Sr := R-SRB Sp = ~2.284 zi . molK Step (2): For the heat capacity of propane, -8.824-107% 2 28,785-10_ K Solve energy balance for final T. See Eq, (4.7). Avs L213 B K t= 1 (Guess) Given Hp = wffa Tle +37 v= Find(t) +6.58 6.59 ( ICPS = 0.394958 ASig = R {ices »()) ASig = 1cps(423, 408.91 1.213,28.785-10"°,-8.824-10" °,0.0) = AS == -Sa + ASig For propane: T T= (100 +273.15)-K 373.1SK Po = I-bar P= 10bar Ty = 1.009 Pa P, = 0.235 Pe Assume ideal gas at initial conditions. Use virial correlation at final conditions HRB(1.00906, 0.23540, 0.152) = ~0,260821 HRB := ~0,260821 SRB(1.00906 ,0.23540,0.152) = -0.179862 SRB := ~0.179862 AH i= R-Te HRB ssa(oe-0(F)} Pri = 0.056 Ty = 1.606 152Use generalized virial-coefficient correlation for both sets of conditions. HRB(1,07095, 0.05578 ,0.094) = -0.052991 HRBj := -0.052991 SRB(1.07095 , 0.05578, 0.094) = -0.034156 SRB := 0.034156 HRB (1.60643, 0.27892, 0.094) = 0.119727 HRB := -0.119727 'SRB(1.60643 , 0.27892, 0.094) = -0.056506 SRBp := ~0.056506 1cPH{400 600, 3.931 ,1.490-107°,0.0,-0.232-10°) = 915.867 1cPs(400,600,3.931, 1.490-10"$,0.0,-0.232-108) = 1.85161 ICPH := 915.867-K ICPS := 1.85161 Eqs. (6.82) & (6.83) are written AH := R-ICPH+ R-Te(HRB2- HRB}) ( P2) AS = tors -ble|]+ R-(SRB> - SRB}) uv 6.60 Carbon dioxide: @ t= 0.224 To B042K — Po := 73.83-bar Tis 31815K P= 1600-kPa_—- Py := 101.33-kPa Throttling process, constant enthalpy, may be split into two steps: (1) Transform to ideal gas at initial conditions, generalized correlation for property changes. (2) Change T and P of ideal gas to final T & P. Property changes by equations for an ideal gas. Assume ideal gas af final T & P. Sum property changes for the process. For the initial T & P: T P T= Tr = 1.046 Pp = — Py = 0.217 Te ue Step (1): Use the generalized virial correlation HRB(1.04586 , 0.216714 ,0.224) = —0.232491 HRB := ~0.232491 SRB(1.04586,0.216714 0.224) = -0.157944 0.157944 183I Hp = R-TeHRB Hg = -587.997— Sp :=RSRB Sp = -1.313 e mol molK Step Q): For the heat capacity of carbon dioxide, pensast we MEI pe suasnadta? Solve energy balance for final T. See Eq. (4.7). ti= 1 (guess) Given E 2(2_,),D(t! Hp eR} AT(t- += -1)+2. 7 [ (Bork 2(=)] c= Find(t) 5 = 0.951 TstT T= 30271K Ans. icps(318.15,302.71 5.487, 1.045-10" 3, 0.0,-1.157-105) = -0.227818 Re ICPS := -0.227818 AS, = (10°59 21) AaSig = 21.087 f P | mol-K AS = -SR+ASig AS 52 Ans. 661 To = 523.15K Po = 3800-kPa P= 120-kPa J : For the heat capacity of ethylene: molK 14.394-10- > 4,392.10" A= 1424 Be co K e (2) For the entropy change of an ideal gas, combine Eqs. (5.14) & (5.15) with D=0: 104 (guess) Given nds) t= 0.589 senfainG)+[ arson? (3 }e-a- oz | : 08, 9K Ansicp1i(s23.15, 308.187, 1.424, 14.394-10°3, 4.30210 IcPH RICPH AHig (b) Ethylene: o To Po To = To = 185317 Py = Pyo = 0.75397 © : Tree = 1.0917 Py = 0.02381 Use virial-coefficient correlation, ‘SRB(1.85317 ,0.75397,0.087) = ~0.10426 SRBo = -0.10426 SRB(1.09170 0.02381 ,0.087) = -0.01374 The entropy change is now given by Eq. (6.83): 5 (guess) Given ASS RIA in(d)+[Betore To (: = ) lt = v-u(F) ist 0. | +SRB— SRBp tau(SRB) := Find(s) T = tau(SRB)-To T = 303.08K At final P and thi r, reevaluate SRB, then T: Ty = 1.0736 ‘SRB(1.07360 0.02381 ,0.087) = -0.01440 SRB := -0.01440 T = tau(SRB)Tp PSBORK Ans. The work is given by Eq. (6.82): 1553 1cpH(523.15,303.11, 1.424, 14.394-1073,-4.392:107 60.0) = -1452.982 1.208 10° ICPH := -1452.982-K AHig = RICPH — AHig = HRB(1.85317, 0.75397, 0.087) = -0.24094 HIRBo := ~0.24094 HRB(1.07360, 0.02381 ,0.087) = -0.02242 HRB == ~0.02242 Hig + R-Te- (HRB - HRBo) \ Ba Po = 30-bar P:=2.6bar For the heat capacity of ethane: 3 — 19,225-1 = 0 Ce SIO K Pe (a) For the entropy change of an ideal gas, combine Eqs. (5.14) & (5.15) with D=0: B t= 0.4 — (guess) Given / AS=R [s n(e+] Ty +C. w()} (¢-1)~ if 3] Posi t= Find(x) t=005 Ti=tTy 367.59K Ans. cpHi(493.15,367.592, 1.131, 19.225.10 4-5.561-10"§,0,0) = -1050.616 ICPH := -1050.616-K RICPH Alig = -8.735x 103 mol We = Aig (b) Ethane: 48.72-bar fe Po Ty = 1.6153 Po 5 Po = 0.61576 6 156At final conditions as calculated in (a) TAT) = TCT) = 1.20404 Py = 0.05337 Use virial-coefficient correlation. SRB(I.61530,0.61576,0.1) = ~0.12314 SRBo ‘= -0.12314 SRB(1,20404 ,0.05337,0.1) = -0.02370 SRB The entropy change is now given by Eq. (6.83): .02370 T= 0.5 (guess) Given AS= RIA Ce a[ Tp+C re(24} fe -1)- »(2) a 2 Po + SRB —SRBg tau(SRB) = ‘ind(z) T s= tau(SRB)-To = 362.69K At final P and this T, reevaluate SRB, then T: T,(T) = 1.18798 ‘SRB(1.18798,0,05337,0.1) = -0.02459 SRB T = tau(SRB)-To T,(T) = 1.18813 The work is given by Eq. (6.82): HRB(1.61530,0.61576,0.1) = -0.26131 HRBo HRB(1.18813,0.05337,0.1) = -0.04158 HRB = -0.04158 10PH(493.15, 362.74, 1.131, 19.25.10" 3, -5.561-107 80.0) = -1086.568 9.034 10° ‘mol ICPH := ~1086.568-K RICPH AH; ig 1576.63 n-Butane: — = 0.200 Te 425K Pe = 37.96-bar Ty=3B1SK — Pos A-bar P J moFK For the heat eapacity of n-butane: 36.915-10 A= 1.935 HRB (0.76017 , 0.02634 0.2) = -0.05679 ‘SRB(0.76017 0.02634, 0.2) = -0,05210 SRBo The entropy change is given by Eq. (6.83) combined with Eq. (5.15) with D = 0: r= 04 (guess) SRB := 0.0 (starting value) Given aS = RIA n(x) -[» Ty +C. na (* . ‘)| (c-1)- “() ist be SRB - SRBg tau(SRB) := Find(z) T <= tau(SRB)-To, T = 375.17K At the final P and this T, evaluate SRB: T t= T, = 0.88254 Pe = 0.20548 Te Use virial-coefficient correlation. ‘SRB (0.88254 , 0.20548, 0.2) = -0.24876 Ts w(SRB)-To T= 381.77K. Although it will make little difference, we recaleulate SRB at this temperture: T eT SRB(0,89806 ,0.20548,0.2) = Tr T, = 0.89806 0.23533 SRB := ~0.23533 188Ts tau(SRB)-Tp Ans. Tr : T, = 0.89722 Te HRB(0.89722 0.20548 , 0.2) = —0.30330 HRB := -0.30330 ‘The work is given by Eq. (6.82): repH(323.15,381.41, 1.935,36.915-1073, -11.402-10" 60.0) 787.744 ICPH := 787.744-K AHjg = RICPH Mig = 6.549 103 Ee be mol We := Aig + R-Te(HRB ~ HRBo) Ans, 6.64 — The maximum work results when the 1 kg of steam is reduced in a completely reversible process to the conditions of the surroundings, where it is liquid at 300 K (26.85 degC). This is the ideal work. From Table F.2 for the initial state of superheated steam: Hy = 3344.62 81 = 7.0854 kg kg From Table F.1, the state of sat. liquid at 300 K is essentially correct: Hy = 112.5- 00-K By Eq, (8.27), Wideat = (H2 - Hi) - Te-(S2- $1) Ans. 6.65 Sat, liquid at 325 K (51.85 degC), Table F.1: Hyig 22 217.02 Stig = 0.7274 Viig s= 1.013 ke kK gm 169Pyat = 12.87-kPa For the compressed liquid at 325 K and 8000 kPa, apply Py ‘= 8000-kPa Eqs. (6.28) and (6.29) with 325-K p= 46010 SK KD Hy = Hig + Viig:(1 ~ B-1)-(P1 ~ Psat) Hy = 223.8815 kJ $1: Stig B-Viig-(P1 - Psat) 8) = 07m For sat. vapor at 8000 kPa, from Table F.2: Hp := 2759.98 Ss: san. Toi 300-K ke kek a 4 KI Heat added in boiler: Q=H)-Hy Q= 2536 8 Maximum work from steam, by Eq. (5.27): Wideat = (Hi —Ha) —To-(S1 Sa) Wiseat = -102982 "i Work as a fraction of heat added: Wi el sa Frac 04058 Ans, ‘The heat not converted to work ends up in the surroundings. + Widea! 7 Sdotg gure = 2M 9, AB Sdotg sun = 50.2344 Te seo Ke kg kW Sdote system *= (81 — Sp)10-<2 SdotG system = ~50.234—— Jot aystem *= (Sy — Sp) 10-2 Ot syst : Obviously the TOTAL rate of entropy generation is zero. This is because the ideal work is for a completely reversible process. 1606.66 Treat the furnace as a heat reservoir, for which Qdot = (6004+273.15-K T= 873.19K Sdotg Ans, By Eq. (5.34) Te = 300-K — Wdotiost := TorSdotg Ans. 6.67 For sat. liquid water at 20 degC, Table F.1: 3.8682 S} == 0.2963: — kg kg: For sat. liquid water at 0 degC, Table F.1: Ho = 0.04 kg For ice at at 0 degC: Hg =Ho-3334 y= 5-284 kg 273.15 keK Hy = 333.44 sy =-121 kg kek kg Ty = 293.15-K mdot ne = 0.32 By Eqs. (5.26) and (5.28): Weotigeat = mdot] H2-Hi-To-(S2-$1)] — Weotideai = 13.686kW Wdotideal “ ‘Wdot = ——— Wdot'=42:77kW Ans. mk 1616.68 This is a variation on Example §.6., pp. 175-177, where all property values 6.69 are given. We approach it here from the point of view that if the process is completely reversible then the ideal work is zero. We use the notation of Example 5.6: J kt Kw 26760 $75 73856 Hy = 00 Hy = 2676055 1 : n= OOF WW $2 1= 0.0 = 273.15-K 7 ig K The system consists of two parts: the apparatus and the heat reservoir at elevated temperature, and in the equation for ideal work, terms must be included for each part. Wideal AHapparatus reservoit ~ To ASapparatus eservoir AHapparatus.reservoir = H2— Hi ~ Q’ Sanparats reservoir = S2~ St kg 50K (Guess) KI i f 0-= = Ho- Hi ~ Q'- To} $2- $1 — ke \ T= Find(T) 7 Ans. (136.64 degC) From Table F.4 at 200(psi): BTU BTU Hy = 1222.6-—— $8) = 1.5737,——_—_— it 420 degF) : bn t Darrinkine "120 de8F) BTU BTU (Sat. tig. Hy 55.51 Hyap = 1198.3-—— hig bas p = 1198.3. be and vapor) BIU BTU Stig = 0.5438-—————_— Sap = 1.5454. i Fprankine Sip = 15458 0.96 162Hy = Htiq + x-(Hyap — Hiiq) $2 := Stig + %-(Svap— Siig) 3 BTU eters Hp = 1.165 x 10 s eal Tin Iby-rankine Neglecting kinetic- and potential-energy changes, on the basis of 1 pound mass of steam after mixing, Eq. (2.30) yields for the exit stream: H = 0.5-H; + 0.5-H2 H= 1193.65 (wet steam) Ans. BTU Stig + x-(Svap ~ Stig) —— tig + (Svap ~ Siig) Ibprrankine By Eq. (5.22) on the basis of 1 pound mass of exit steam, 6.70 3 1.3496 © Ibm Bru 118.0=— bm VOL tig = miig?Viig VOLtig = 79.796 8° VOLyap := Viank ~ VOL tig, VOL yap = 0.2048° VOL vay Myap = a mMyap = 0.151 Ibm Vyap 163ig Uiig + Map Uv eae U; = 406.726 BU + Myap Ibm By Eq. (2.29) multiplied through by dt, we can write, (Subscript t denotes the contents of the tank. Hand m refer to the exit stream.) d(m;-U,) +H-dm Integration gives: my-Up—m-Uy +f Hdm=0 0 From Table F.3 we see that the enthalpy of saturated vapor changes from 1203.9 to 1203.1(Btu/Ib) as the temperature drops from 430 to 420 degF. This change is so small that use of an average value for H of 1203.5(Btu/Ib) is fully justified. Then my-U2—my-Us + Have'm = 0 Haye= iana.s STC Pee ee ‘mp(mass) := my ~ mass Property values below are for sat. lig. and vap. at 420 degF 3 Vvap = 1.4997. BTU Uyap == HIT —— sp be 7 . = Vo(mase) = Van Ema) seo cee mp(mass) Vvap - Vig Up(mass) := Ulig + x(mass)-(Uyap — Utiq) mass = 50-Ibm (Guess) Gaetan teem) Haye ~ Uz(mass) mass := Find(mass) 6 Ib Ans. 1646.72 The steam remaining in the tank is assumed to have expanded isentropically. Data from Table F.2 at 4500 kPa and 400 degC: $1 = 6.7093-—— amk ee J By interpolation in Table F.2 S2= Si = 6.7093 at this entropy and 3500 kPa: 3 Vo 1= 78.726. gm Vtank my = Vi This problem is similar to Example 6.7, where it is shown that Q= A(meH) ~ H-Am, Here, the symbols with subscript t refer to the contents of the tank, whereas H refers to the entering stream. We illustrate here development of a simple expression for the first term on the right. The1500 kg of liqui ly in the tank is unchanged during the process. Similarly, the vapo in the tank that does NOT condense is unchanged. The only two enthalpy changes within the tank result from: 1. Ad ion of 1000 kg of liquid water. This contributes an enthalpy change of tig Am, 2. Condensation of y kg of sat. vapor to sat. liq. ‘This contributes an enthalpy change of (Hig — Hvap) = -y-SHyy Thus A(mpH) = Hig: Am,—y-AHyy 165A(meV,) = Viger = ¥-AViy Whence Q= HhigrAm, = y-AHyy — H-Amy ‘Am, != 1000-kg Required data from Table F.1 are: At 50 degC: n= 2093-8 kg At 280 degC: Hig = 1085.8 kg nay kg Vig’ hee 5.641 kg, Vy Q = Amp(Hiiq- H) —y-AHiy Qs Ans 6.73 Given: Veonk = 0.5m? fa CH04— Ty = 295K Mink *= 30-kg kgK Data for saturated nitrogen vapor: 80 1.396 0.1640 85 2.287 0.1017 90 3.600 0.06628 95 |-K 5.398. |-bar V =| 0.04487 100 1.718 0.03126 105 10.83 | 0.02223, 10, 14.67 0.01598 168 lB8.9 82.3 At the point when liquid nitrogen starts to 85.0 accumulate in the tank, it is filled with saturated ky Vapor nitrogen at the final temperature and having H=| 86.8 eg properties | 87.7, Map, Tvaps Vvap>Hyvap»U vay |e 3: Tvap» VvapHyap,Uvap 85.6 By Eq, (2.29) multiplied through by dt,d(ny Ut) — H-dm = dQ Subscript t denotes the contents of the tank; H and m refer to the inlet stream, Since the tank is initially evacuated, integration gives MWvap Uvap ~ Hin-Myap = Q = mtank-C-(Tyap-T1) (a) v, Also, Map = @®) Voap Calculate internat-energy values for saturated vapor nitrogen at the given values of T: (56.006 —. U-=(H-P-V) 59.041 61.139 U =| 62.579 z 63.395 : 63.325 (62.157) Fit tabulated data with cubic spline: Us := Ispline(T,U) Vs := Ispline(T,V) Uyap(t) == interp(Us,T,U,t) Vyap(t) = interp(Vs,T, Vt) Tyap:= 100K (guess) 1676.74 Combining Eqs. (A) & (B) gives: Given MankC-(T1 ~ Tap): Vvap( Toa Uvap Trg) ~Bin = spam To) Yo) Tyap = Find(Tyap) Tyap = 97.924K Viank ae ap Tvap vane TA82lkg Ans. ‘The result of Part (a) of Pb. 3.15 applies, with m replacing n: my-(U2-H)-mj-(U)-H) = Q 50 Whence my-(H - Ua) = m-{H - Uy) Also Un = Ujig.a + X2-AUyy.2 Hi : Veank V2 = Viig.2 + X2°AViy.2 Ve ™ Eliminating x, from these equations gives : ie St Vig m2 mo} H = Uliq2 = —a—— AU wa] = me(H = Ui) we which is later solved for my my 3 16000-kg Vy = 3.125% 107 3 kg Data from Table F.1 @ 25 degC: 3 a: Viig.t := 1.003- AVyy1 = 43400 gm gm 1686.75 AU yy. = a0. Ur = Utig #x1-AU jy. x1 = 4.889% 1075 Us = 108.913 Data from Table F.2 @ 800 kPa: 3 Viig2 = 1.115- Uiiga am cm I AViy.2 $= (240.26 ~ 1.115) 2 = (2575.3 ~ 720.043)-— gm kg mi 3 kl AViy.2 = 0.239 — AUjy2 = 1.855 x 10° ke ie kg : 7 i Data from Table F.2.@ 1500 kPa: H:» 2789.9-— 2 (AUiw2 my-(H = U)) + Veaak la ee my = 2.086% 10°kg H-Ulig2 + Viig2'| ws) ~ Ulig2 + Viig2 \A¥v2 steam = my ~ my Ans. The result of Part (a) of Pb. 3.15 applies, with ny = Q Whence U2 =H From Table F.2 at 400 kPa and 240 degC 169= 2043.94, _ Interpolation in Table ¥.2 will produce values of t kg and V fora given P where U = 2943.9 ki/kg. 1 384.09 ) 303316 100 384.82, 3032.17 200 tz =| 385.57 V2 := | 1515.61 300 386.31 1010.08 400. 387.08 757.34 5 Veank = 1.752 6.76 x= 01 3 Vi = 7957x103 my = 257.832kg kg 170‘The process is the same as that of Example 6.7, except that the stream flows out rather than in, The energy balance is the same, except for a sign: Q= A(me Hi) + H- Amant where subscript { denotes conditions in the tank, and H is the enthalpy of the stream flowing out of the tank. The only changes affecting the enthalpy of the contents of the tank are: 1. Evaporation of y kg of sat. lig.: y-(Hvap— Hliq) 2Exitof 0.6mi-ke of -0.6-my "Hig ‘Thus (mH) = ¥ (Hyap ~ Hig) - 0.6m): Hhig si ilarly, since the volume of the tank is constant, we can write, A(my Vi) = ¥(Vvap~ Viig) ~ 0-6-1 Viig = 0 0.6-my-Vij Whenee y= LO Via Wap ~ Vig 0.6-m1-Viig -(Hivap — Htig) ~ 0.6-m)-Hiig + H-Amanic Veap~ Vig But H=Hiq and 0.6-m, = Aman and therefore the last two terms of the energy equation cancel: 0.6-m1-Viig = “(Hyap ~ Hic Yop Vig tet) 1716.77 Data from Table F.1 for sat. liq. Thy = 1006-42 @4 degey Hy = 3559-2 (85 dege) ke kg Data from Table F.2 for sat. vapor @ 400 kPa: Hy 273768 kg By Eq. (2.30), neglecting kinetic and potential energies and setting the heat and work terms equal to zero: H3-mdots ~ Hy-mdoty ~ Ha-mdotz = 0 Also mdot, = mdot3 ~ mdot mdots : yhenes mdots-(Hi - Hs) Whence dot := (Hi - #3) Hi —H2 Ans. Table F.2, superheated vap., 3000 kPa, 375 degC: kJ Ho = 3175.64 Sys ig Table F.1, sat. liq. @ 50 degC: kg Hy Stig ?= 0.7035-—. a a kek 172Find changes in H and S caused by pressure increase from 12.34 to 3100 kPa. First estimate the volume expansivity from sat. lig, data at 45 and 55 degC: 3 AV = (1015-1010. a= 10K P= 3100-kPa gm 3m? 4 avesx1g 3S B= 4941x104! gm Apply Eqs. (6.28) & (6.29) at constant T: Hy := Hig + Viig-(1 ~ B-T)-(P ~ Psat) Hy = 2119268 8 ki $1 Stiq- B-Viig:(P ~ Psat) 51 = 0702 By Eq. (2.30), neglecting kinet and work terms equal to zero: c und potential energies and setting the heat Hg-mdot3 ~ Hy-mdoty ~ Hy-mdot = 0 Also mdotg = mdot3 — mdoty mdot3-(H3 - Ho) Whence —mdoty == maoty $8922 Ans. Hy =H SLES see kg mdoty = mdot3 ~ méaty mdoty = 13.1152 see For adiabatic conditions, Eq, (5.22) becomes Sdotg := S3-mdots ~ Sy-mdoty ~ Sz-mdoty I. Sd 193 — Ans. eT eK The mixing of two streams at different temperatures is irreversible. 4736.19 Table F.2, superheated vap. @ 700 kPa, 200 degC: w i Hy == 2844.2. $3 = 6.8859 3 ke 3 kek Table F.2, superheated vap. @ 700 kPa, 280 degC: ny = 30177-2 $1 = 7.2250 dot = 50-48 ke ek see Table Ft, sat. ig. @ 40 deg J Siig = 0.5721- ig ard By Eq, (2.30), neglecting kinetic and potential energies and setting the heat and work terms equal to zero: Hp Alig Hg-mdots ~ Hy-mdot) — H2-mdot = 0 Also mdot; = mdotz + mdot; mdot)-(Hi - Hs) Hy — Hp a For adiabatic conditions, Eq. (5.22) becomes mdoty == S2:= Siig dots := mdotz + mdoty Sdotg mdoty ~ Sz-mdotg Ans. ‘The mixing of two streams at different temperatures is irreversible. 6.80 Basis: 1 mol air at 12 bar and 900K (1) +28 mol air at 2 bar and 400K (2) =3.5 mol air at T and P. 1746.81 Ty == 900K Ssmol ms tmol ms Ist law: T := 600-K (guess) Given ny-Cp-(P- Ty) +n2-Cp-(T-T2) = 0-3 T = Find(T) 2nd law: Given Find(P) i molwt := 28.0142 cp = 0.248 BTU _ Tbmol Tbqyrankine M, =steam rate in Ibm/see Ibm My = nitrogen rate in Ibm/see Mp = 40-—2 sec (1) = sat. fig. water @ 212 degF entering (2)= exit steam at 1 atm and 300 degF @)= nitrogen in at 750 degF Ty = 1209.67-ankine (4) = nitrogen out at 325 degF Ta = 784.67-rankine Hy t907-BTS St (Table F:3)6.82 Hg := uia¢ BE sy = 181582 (rabte 4) 1m mrankine Eq. (2.30) applies with negligible kinetic and potential energies and with the work term equal to zero and with the heat transfer rate given by Ibm My:= fbn (guess) Qe -60.BTU M, _ Tbin Given Mp(Hp~H1)) + My:Cp-(T = Ts) = ~60- 7 M; := Find{Mg) Ans, Eq. (8.22) here becomes Sotg = My(So ~S1) +Mo(S4~S3)- 2 To Ts S4-S3 = Cp-ln| — T3, Te = 529.67-rankine mobwt := mol PD molt M, = steam rate in kg/see M, = nitrogen rate in kg/sec Mg := 20- (1) = sat. lig. water @ 101.33 kPa entering (2) = exit steam at 101.33 kPa and 150 degC G)= nitrogen in @ 400 degC (4) = nitrogen out at 170 degC Tar 443.15-K 176ki Hy 2 419.064 Sus lek (Table F.2) wu i Ha: me a— S2- 1.6075 (Table F.2) ic and potential energies and setting By Eq, (2.30), neglecting ki the heat transfer rate given by the work term to zero and wi (guess) ‘Ms ‘= Find(Ms) Ans. Eq, (6.22) here becomes Sdotg = Ms (S2-S1)+Ma(Se~ $3) - 2 Ts kl Sa~S3 = Cpin| == Tg *298.15K — Q = -80- My 8 6.86 Methane =1; propane =2 Ti=363.15K P= S500-KPa yy = 0.5 yel-y © = 0.012 oy = 0.152 Ze = 0.286 2g = 0.276 Tel = 190.6K T= 3698K Pop = 42.48-barThe elevated pressure here requires use of either an equation of state or the Lee/Kesler correlation with pseudocritical parameters. We choose the latter. Tpe *= yr Tet + y2°Te Poe = yirPet + y2"Pea The = 280.2K Pye = 44.235 bar T Pp Tpr = = Tpr = 1.296 Por = —— maT ot Pcie Por = 1.243, By interpolation in Tables E.3 and E.4: ZO := 0.8010 =yraytyz@2 — @ = 0.082 W+@Zl Z=08l For the molar mass of the mixture, we have: molt := (y1-16.043 + yo 44.097) molwt = 30. oe mol mol 3 T v= 14.799 mdot == Pemoiwt am Vemdot Vdor = 2.07% 10S a= YE = G 901m? sec a D=2964em Ans. 1786.87 Vectors containing T, P, Te, and Pe for the calculation of Tr and Pr: 500 425.2 20 42.77) 400 304.2 200 73.83 450 552.0 60 79.00 600 6177 20 21.10 620 617.2 20. 36.06 a Ts Piz Poss an 250 190.6 90, 45.99 te Te 150 154.6 20 $0.43 fo 500 469.7 10 33,70 Pres ee 450 430.8 35 78.84 Pe 400, 374.2, 15 40.60. Ta7e O86 1308 2708 Dai 0780) 0.871 0948 pe = [1008 pr = [55 7312 1957 037 0387| 7,065) 0287 "as oad] 7,060) 0.369) Parts (a), (2). (h). ‘500 20 425.2 42.77 190) 150 20 154.6 50.43 022 500} 33.70 |-bar @ ==] 252 450 35 430.8 78.84 245 400. 15, 374.2 40.6 327, Tre 1791.176 0.468 0.97 0397 Tr =| 1.065 Pr =| 0.297 1,045 oad 1.069 0369 ———= 172 0139-2 (3.62) re? — 722 DBO (6.80) pBi = & (6.81) Te (0.253 ae ) (0.483 0311) 0.37 see 0.73 oass| Bo =|-0309} Bi =| 6.718 10° | DBO =) 0574} DBI =} 0.522 | 0.321 4217x1073 | | 0.603 0.576 | ‘ie { \-0.306 009x107? } (osex Losi) Combine Eqs. (3.58), (3.59), and (6.40) and the definitions of Tr and Pr to get: VR i= [k Te (Bo +0 Bl) Pe HR :=[R-Te-Pr| BO-TrDBO+o(B1-TeDB)]) 78) ai teueieieecneet SR :=[-R-Pr(DB0+o-DB1)} (6.79) 180-1377x10° fags (-200.647 ae 94.593 |, aq ae 2.469 i | cm HR =| -1226x10° | sr =| 1.74 vr = |-355.907 | =a] mob | 146.1 =1.746% 10° eles | 3) a \9282.454 =1.251« 10) fae Parts (b), (c), (d), (@), and (£) -- By Lee/Kesler correlation: By linear interpolation in Tables E.1—K.12: 9 1 (HR) (HR) HR DEFINE: h0 equals hi equals “Sh equals TR : RTe ae RTe fe RTe 0 1 (sR) (sR) SR 0 equals ———— si equals ——— s equals —— ‘q R eq R ql R ( 663 0.208 ‘2.008 228) 124 =050 $121 278| Zi =| -.088 2.970 783 =.036 0,671 0.596 707 0.138 = 1.486 0.169 —1.137 0.405 4.381 5.274 2.675, 2.910 0.473 0.557 0.824 0.289, 400 200 304.2) 224 450 60 552.0 au T:=| 600 |-K P=} 20 |-bar Te :=| 617.7 |-K @ =| 492 620 20 6172 303 250 90 (isa6 012 181oe — + Z0+oZ1) B54) h:=(hO+a-h1) (6.76) s:=(s0+as1) (6.77) —— heTorR) O71 0.118 Z=| 0.235 0.772 0. 700) AR || 597396 67.284 ‘The Lee/Kesler tables indicate that the state in Part (c) is liquid. 6.8 Vectors containing T, P, Tel, Te2, Pel, Pe2, wl, and 2 for Parts (a) through (h) 650 60 562.2 553.6 300: 100 304.2. 132.9 600 100 304.2 568.7 ss /K oP bar Tel = pie /K Te2 oa K 200 15 1906 126.2 450 80 190.6 469.7 250 100, 126.2 154.6 18248.98 40.73 210 210) 73.83 34.99 224 048 B83 24.90 | 224 400 48.72 50.40 .100 .087 29.63] P| gs.00 094 *| 012 45.99 34.00 012 038 45.99 33.70 012 252 \ 34.00. 30.43, 038, 022, ——__— > —— Tpe i= (5:Tel +.5-Te2) Ppo := (.5-Pel + .5-Pe2) S-ool + 5-092) T - Tpr:= ra Ppr:= oe 557.9 44.855 0.21 218.55, ( 54.41 0.136 436.45 | 49.365 | 0312 293.8 49.56 | 0.094 Tpe = K Ppe = bar o= 282.05 | 67.81 0.053, 330.15 | 39.845 | 0.132 \ 140.4 } lanais/ (0.03 (1.165 (1.338 1.373 1 “| 1.375 2.026 1.191 1.913 Tr) aig Pers) 912 1,263 1.875 1.363 2.008 (1.781 2.369 183,Lee/Kesler Correlation --- By linear interpolation in Tables E.1—-.12: 6543 219 ~1.395 ~461 7706 .1749 -1217 =116 7527 .1929 -1346 097 ‘ws 6434 : 1501 hose —ESLO hi: ~400 7744 1990 1.340 049 6631 1853 1.623 254 7436 1933 “1372 =.110 9168. 1839, 0.820, 0.172 =.890 466 658 235 -n9 2402 944, 430, =.704 224 965 =348 750 250 =.361, .095, 0 equals ca? hi equats cue), equals : RTpe Ripe RTpe sO equals (sx? sl equals feqae R R (20 + w-Z1) (3.54) (no+e-h1) (6.76) SS (s0+@-s1) (6.77)WA 14 18 Chapter 7 - Section A - Mathcad Solutions 28922 cp mol With the heat, work, and potential-energy terms set equal to zero and with the initial velocity equal to zero, Eq. (2.32a) reduces to uz aH+—-=0 But AH = Cp-AT Whence aT From Table F.2 at 800 kPa and 280 deg Hy = 30149 8) = 7.1595 kg keK Interpolation in Table F.2 at P = 525 kPa and S~ 7.1595 kd/(kg*K) yields: 3 k Hy = 2855.2. Vo = 531.21 mdot :='0.75-—= ke gm sec With the heat, work, and potential-energy terms set equal to zero and with the initial velocity equal to zero, Eq, (2.32a) reduces to: Whence Ans. mdot- V2 By Eq. (2.27), a= Ans. up ing problem may be earried out for a series of exit pressures until a minimum cross-sectional area is found. The corresponding pressure is the minimum obtainable in the converging nozzle. Initial property values are as in the preceding problem. 186wy Sy = 7.1595-—— S)= 8} kgk Interpolations in Table F.2 at several pressures and at the given entropy yield the following values: ‘400 2855.2 S312 425 2868.2 307.12 P:=| 450 |-kPa asso.7 | 435.45 | kg em. 475 2892.5 465.69 500, 2903.9 447.72 — eee mdot-V2 uy = f—2(Ho - Hy Ags= uw 565.2 7.05 541.7 7.022 uy =| 518.1 )™ ‘Ap =| 7.028 fem? see | 494.8 7.059 lan 2 7.127 Fit the P vs, A2 data with cubic spline and find the minimum P at the point where the first derivative of the spline is zero, iss pis Pi 3, = Aa, s := cspline(P,A) A(P) = interp(s,p,az,P) 00-kPa (guess) a cm Given 4 _A(pyain) = 0 = ae (Poi) = 0 Pmin ?* Find( nin) Ans. \ (Big) 7.021em? Ans. 187Show spline fit graphically: := 400-kPa,401-kPa...500-kPa 23 tt 1 7 / LE Boo 7.07 A@) om 7.05 7.9 From Table F.2 at 1400 kPa and 325 degC: Hy = 3096.52 $1 = 700499. $2 =8} ke kg-K Interpolate in Table F.2 at a series of downstream pressures and at S 7.0499 kdi(kg*K) to find the minimum cross-sectional area. 800 2956.0 294.81 715 2988.5 30212 |, ki com 750 |-kPa Hp =| 2940.8 | Va =| 309.82 725 2932.8 | 317.97 700. 2924.9, 326.69. 188740 Since mdot is constant, 5.561 the quotient V2/a2 is a measure of the area. Its a ‘minimum value occars very 5.552 close to the value at a 5577 vector index i=3. At the throat, Ag = Gem? Agua, imdot = Logi t& Ans. noes ae V: 25 At the nozzle exit, P= 140 kPa and S = S1, the initial value. From Table F.2 we see that steam at these conditions is wet. By interpolation, ky 4098-— s ke-K vee From Table F.4 at 130(psi) and 420 degF: Hy v= 1233.68 Sy = 1.63102 ba Ibpyrankine 242 uP aw By Eq. (2.322), ce eau aH =-7338" 2 Ibn Hy +H Fy = 1154828 From Table F.4 at 38(psi), we see that the final state is wet steam: 1167-8 Din Btu ibgrrankine Hyap Svep = 1.6872 189)TAI 712 0.987 (quality) BTU 82 = Stig + ©(Svap — Si 82 = 1.67 a+ (Svap~ Stig) a Ibpyrankine Sdotg := $2 S} Ans. wick 2 molwt By Eq. (2.320), But AH= Cp-AT Whence AEST Initial t= 15 + 167.08 = 182.05 degC Ans. Values from the steam tables for saturated-liquid water: 3 AIS degC: V := 1.001 288.15-K em Enthalpy difference for saturated liquid for a temperature change from 14 to 15 degC: (67.13 ~ 58.75) At 2K cp = a em ‘At I stam P49 Apply Eq. (7.25) to the constant-enthalpy throttling process. Assumes very small temperature change and property values independent of P. 190ar BT) AP AT = 0.093K cp (a BOD od =| ‘The entropy change for this process is given by Eq. (7.26): AS = Cp T+AT) _py.ap AS = 1.408 x 1073 tT) gmk Apply Eq. (5.36) with Q=0: To = 293.15-K Wlost «= To-AS TAB~TAS R= 8.314 P2:= 1.2 350 80 304.2 73.83 224) 350 60 282.3 50.40 087 The Pls Tes Pe = os 250 60 126.2 34.00 038 400, 20 369.8 42.48 152 5.457 1.045 “1.157 1.424 0.0 14394] 10 c 3.280 a) 1.213, 28.785. As in Example 7.4, Eq, (6.84) is applied to this constant-enthalpy Process. If the final state at 1.2 bar is assumed an ideal gas, then (A) of Example 7.4 (pg. 258) applies. Its use requires expressions HR and Cp at the initial conditions. 0.040 0.0 Eq. for List 1.084 a Tl 124 1g Tes Tr= Pr= Te 1.981 1.765 (1.082, 0.471} 1917.13 Redlich/Kwong equation: Q := 0.08664 _— Bes (2 2) (3.50) Guess: I Zz Given = 1+B-a8 2(6.,q) == Find(z) +B;) isl I =o 200 *) (6.62b) ZABi Gi, Rj == R-THi{(Z(B;.qi) ~ 1) ~ L.S-qrli] (6.64) The derivative in these SRi == R-(In(Z(Bi,4)) Bi 0.5-qi;) (6.65) equations equals -0.5 The simplest procedure here is to iterate by guessing T2, and then calculating it. Guesses 2(61.a) (2.681 10° “8.177 9773) 2.253 10° etee racaa oaee| | \ 233 J =1.396 x 10°) 1927.14 Soaye/Redlich/Kwong equation: Q := 0.08664 W = 0.42748 —_______ (0.480+ 1.5740 - 0.1760") a 2B 3.49) 2(8,4) = Find(2) ; s) (6.62b) 26.4) : if 20.8)- I af (my a | «| oot) (ai) 4 SR = x) meto.a) -B 6.65) (Tr)? ‘The derivative in these equations equals: ~«(3] Oy Now iterate for T2: Guesses 2(6;,ai) = 3 O75 2.936 x 10° eee) 2 O79 3 3 oe x 10° 4.769 | 300 tos] «HR =| 7956 SR= Ths 0868] 526.246 -1.789 | 232 Fi a | -1.523% 10° ) 2.679. (384) Pe -[rardeene Eni DB | 7 rT’ || 193TAS 37464 + 1.54226-0 — 0.269920") — = Pr Wea =[QA2] 650 =|) osr : ( " cen ‘ ) : Guess: zl Given 2=1+B-gB- ney (349) z(,q) == Find(z) id (a ol Seale ) (6.62b) 22 ZIBi.ai) +e ein) SR = neta) aa »(2}'s 1 (6.65) HR; = (15) The derivative in these equations equals: ele 4 104Now iterate for T2: cae 26: (-so41x 10 6.152) one 3 4.784 | 2.459% 10° ~ - HR =| -7459* 19] gp a 600.376 ~1.847 O35 i ~ 1.581 « 10" fee ae see sceeseseeseset 12 748 Hy = 3462.9. By Eq. (7.13), mdot := an Ans. For isentropic expansion, exhaust is wet steam: Stig 2= 0.8321 ie Svap = 79094 x= 0.92 (quality) 195 cps] RAs Bice + S244 1) +2 z - oT? 270 297 229 383, T2= Ans, S2= 8)ks Hyap := 2609.9-— ms kg Hp = Hig + (Hyap- Hig) H'g = 2.421 x 10° 2 Hp- Hy H2-H) 7.19 The following vectors contain values for Parts (a) through (g). For intake conditions: kJ Ky 32743. 65597 kg kek sso.e 2 esis . = 0.80 3634.5. 6.9813 0.7 kg kek 0.82 3161.2: Ag. 6.4536- pis 0 kek 0.75 0.75 id oan psa Bu 0.75 1.6000 Tbgerankin€ Buu Buu 1389.6.— 1.5677-——_— Dm Ibprrankine 196For discharge conditions: ki J 0.9441-—_ 7.7695: —— kgk ( kek 0.8321. 19094 ek eK i ig 0.649: 8.1511-—— kek Ww J w=| bos =| 7507 Stiq = kek Syap = kek 15301 7. 68S. igk kek Bu Bu 0.175024 1.92002 Tbyerank ibjrankine 0.220024 1.8625. bavrankine Tarrankine 2893022 2625.44 80- ke kg kg s 251.453 2609.9. kg kg 191.832 2584. gt 70 48. ke ke ky kK Hig =| 3405645 | Hap =| 2086057 504. ore 2706.3-4 ke kg Bu Btu Ib 94,03-— 16.15 — |. Bm Bin 10 120.99.B% 1273-34 100.0" bm bm see 197S1= Stig ——____ > NQis Hp := [ Hlig + ¥’2-(Hyap ~ Hig) } © Syap~ Siig aimee > AH := [n-(H’2-Hi)] Hp =H) +AH Wot := (AH-mdot) ——— ow 2 Mtg Tonawls..os,.)) 0 Hig S2:= [Stig + x2-(Svap ~ Stig) J K Ans bar R= 8314 He mole-K J molK 720° T:242315K Po? For isentropic expansion, For the heat capacity of nitrogen: 198721 0.593-10* K 1D = 0.040-10°-K? A:= 3.280 For the entropy change of an ideal gas, combine Eqs. (5.14) & (5.15) with C=0. Substitute: T= 05 (guess) Given AS= nA mies] Ans. Find(t) To= ‘Thus the ini Ty 1223.15-K J mol Cp ss 32+ Eqs. (7.18) and (7.19) derived for isentropic compression apply equally well for isentropic expansion. They combine to give: Ws = -15231 mol Ans. Ans. 199Te = 408.1-K 36.48-bar —@ := 0.181 Po = 5000-kPa =P == 500-kPa For the heat capacity of isobutane: 37,853-10"> crn rilegass107® K e Tyo = 1.282 Pro = 1.3706 Use generalized second-virial correlation (borderline at TO, but good enough): HRB(i.282, 1.3706,0.181) = -0.940291 HRB := ~0.940291 SRB(i.282, 1.3706,0.181) = ~0.534176 SRBo := -0.534176 The entropy change is given by Eq. (6.83) combined with Eq. (5.15) with D = T= 05 — (guess) SRB = 0.0 (starting value) Given AS = Rj A-In(t) 4 [» To +C-To- ()]« —1)-1n if) uJ 42 Po) +SRB - SRBo tau(SRB) := Find(z) T := tau(SRB)-To 443.37K At the final P and this T, evaluate SRB: TCT) z T,(T) = 1.0864 P, = 0.1371 SRB(I,0864,0.1317,0.181) = ~0.082852 SRB := -0.082852 Do a further iteration for T: T := tau(SRB)-To T = 445.65K T,(T) = 1.09202 SRB( 1.09202, 0.1317,0.181) = ~0.081601 SRB := -0.081601 T:= tau(SRB)-To T = 445.62K T-(T) = 1.0919 200‘The enthalpy change is given by Eq. (6.82): HRB(1.0919,0.1317,0.181) = -0.126003 1p H(523.15,445.62, 1.677,37.853:10 >, -11.945-10" §,0.0 RICPH — AHig = -1 1.089 ICPH := -1333.811-K Aig nal $326.5 mol AH! = AHig +R-Te-(HRB ~ HRBo) AH The actual enthalpy change from Eq. (7.16): 08 — ndot= 700M ate aH AH = ~66612— ‘sec. mol Wot = ndot-AH Woot $'=4662:8kW Ans. ‘The actual final temperature is now found from Eq. (6.82) combined with Eq, (4.7), written: t= 0.7 (guess) Given AH R. Ato(s=1)+ Brel? $a? (3 J +Te(HRB — HRBo) tau(HRB) := Find(z) T := tau(HRB)-To T = 457.88K Although it makes little difference, we recalculate HRB at this temperature: Te(T) = 1.122 HRB(1.1220,0.1317,0.181) = -0.119069 HRB == -0,119069 T = tau(HRB)-To 7.23 From Table F.2 @ 1700 kPa & 225 degC: 851.02 81 65138 ke ek 2017.24 For At 10 kPa: Hig = tora dot := 05-48 sec Hy := Mig + X2-(Hvap- Hlig) AH = H)-Hy Ep = 2.465 10° an = -385.g48 kg kg (a) Qdot := mdot-AH — Wdot Ans. (b) For isentropic expansion to 10 kPa, produ S1~ Stig 19 wet steam: Hhig + ¥'2-(Hyap ~ Hig) wap = Stig 2 aera Hy = 2.063% 10° = kg Wdot' := mdot-(H'- Hj) Ans. To = 673.15-K I-bar For isentropic expansion, I motK For the heat capacity of carbon dioxide: A= 5.457 Bs D ss -1.157-10°K? the entropy change of an ideal gas, combine Eqs. (5.14) & (5.15) with C= 0: 1.5 (guess) 1 Given AS= n{Ants[are + a ; (=) (c-1)- (n a }728 1 = 0,693, .= Find(s) = 1-To ICPH(673.15 466.456, 5.457, 1.045-10”*,0.0,-1,157-1 ICPH := -1174.8¢-K AH = RICPH 0.78 Work := AH’ (AH := Work AH = -7. 326-8 mol For the enthalpy change of an ideal gas, combine Eqs. (4.2) and (4.7) with C= 0: Given r Hi SHER Atole-)+Bagel?-i)-2{2 ‘) 2 Toe t= Find(z) += 0.772 wT T= 519.9K Ans. Thus the final temperature is 246.75 degC Vectors containing data for Parts (a) through (¢): 500 6 371 12 3.5 450 3 376 20 40 Th=] 525] Pri=]10] t2:=|458] P2:=]3.0] cp=|55/-R 475 7 32 15 45 580 4 403 12, 2.5 — Cp(T2- TD] Ideal gases with constant heat capacities see ee eee [ R (7.22) Applies to expanders as q cpTl (2) ° || wellas to compressors Pl 2037.26 ndot:= 175 T1:= 550 PL? Guesses: = 0.75 Wdot := 600 Given. [ a & anendot-3.5-R-TL (@) -1 Wadot = ——— ee 7 = 0.065 + 0.08-In(Wdot) 10 ( Wdot [ Waoe! ) = Find(Waot,n) n For an expander operating with an ideal gas with constant Cp, one can show that: T2 = 433.213 By Eq. (5.14): as=r{& (2) - (2) AS = 6.435 R TI \Pi}} By Eq. (5.37), for adiabatic operation : Sdotg = ndot-AS ‘ Ans. 2047.27 Properties of superheated steam at 4500 kPa and 400 C from Table F.2, p. 714: HI := 3207.1 Sls 5.7093 saturated vapor, then ig. 7.4) must produce If the exhaust steam (Point 2, Fig. 7.4) is "dry, isentropicexpansion to the same pressure (Point 2', "wet" steam, withentropy: S2= 1 = 6.7093 = (x)(Svap) + (1-x)(Sliq) [xis quality] A second relation follows from Eq. (7.16), written: AH = Hvap - 3207. (N)AH) = (0.75)] (2)(Hivap) + (1-x) (Big) - 3207.1] Each of these equations may be solved for x. Given a final temperature and the corresponding vapor pressure, values for Svap, Sliq, Hvap, and Hlig are found from the table for saturated steam, and substitution into the equations for x produces two values. The required pressure is the one for which the two values of x agree, This is clearly a trial process. For a final trial temperature of 120 degC, the following values of Hand S for saturated liquid and saturated vapor are found in the steam table: 503.7 Hy = 2706.0 Sl = 1.5276 Sv = 7.1293 ‘The two equations for x are: _ Hy 801.7-.75-HI 75-(Hv — HD) XH The trial values given produce: These are sufficiently close, and we conclude that: t=120 degC; P=198.54 kPa If were 0.8, the pressure would be higher, because a smaller pressure drop would be required to produce the same work and AH. 2087.29 7.30 PLs= atm, PQ:=tatm = Ths 15C n= 0.55 Data in Table F.1 for saturated liquid water at 15 degC give: Eqs. (7.16) and (7.24) combine to give: AH = -V-(P2—P1) Ws i= AH (7.14) AH - V-(P2 -P1) Eq. (7.25) with B=0 is solved for AT: AT. a P Assume nitrogen an ideal gas. First find the temperature after isentropic expansion from a combination of Eqs. (5.14) & (5.15) with C= 0. Then find the work (enthalpy change) of isentropic expansion by a combination of Eqs. (4.2) and (4.7) with C= 0. The actual work (enthalpy change) is found from Eq. (7.20). From this value, the actual temperature is found by a second application of the preceding equation, this time solving it for the temperature. The following vectors contain values for Parts (a) through (e): (7s 6-bar I-bar 673.15 S-bar I-bar TTBAS |-K 7-bar P:= | L-bar 723.15 8-bar 2-bar | 758.37 95-psi 1s-psi) 200 0.80 150 0.75 adot 175 ies 0.78 100 a 0.85 0.5-453.59 0.80 Ri Bale 206For the heat capacity of nitrogen: 3 0593.10 "= 0,040-10%.K? Tau(To.Po,P) := Find(t) 11 = Tau(To, Po, Pi) (460.67 431.36 = | 453.48 |K 494.54 455.14, T= To,ti rcphi( 753.15, 460.67,3.280,0.593-10" 3,0,0,0.040-105) = —1167.969 1cpHi(673.15,431.36,3.280,0.593-10" 3,0.0,0.040. wa 875.585 1cpr(773.15,453.48,3.280,0.593-10" 3,0.0,0.040-105) IcPH(723.15, 494.54, 3.280, 0.593-10”°,0.0,0,040-10°) = 834.936 1CPH(755.37,455.14,3.280 0.593.107? ,0.0,0.040-10°) = -1096.005 =1168.427 -1167.969)) (- 9710.3) 875.585 -7279.6 7 ICPH := } -1168.427 /K AH’ := R-ICPH AH’ = | -9714,3 (inal 834.936 | 6941. -1096.005 ) \-91 aio 207AH = | ~7577.2 | — AHS [stole +8 rele JP Tau(To,AH) = Find(t) 71 = Tau(To, | 529,34 ‘AS16.28 7.31 Property values and data from Example 7.6: Hy 3301.64 Si= 6.6858 mdot = 59.02.48. kg kek see Hp := 2436.0. 82 = 7.6846. Wot := -56400-kW ke kek Ty = 300-K By Eq. 6.26) Weotigeat = mdot| H2~H1-Te-(S2-Si)] Wotideat = -74084 KW Wot nes mes0.761. Ans. ‘dotideal The process is adiabatic; Eq. (5.33) becom Sdotg := mdot-(S2 - $1) Sdotg, 149 - Ans, Wabotjost = To Sdotg ‘Waottoct = 17685k\ Ans. 2087.32 For sat, vapor steam at 1200 kPa, Table F.2: Hp = 2782.7. $2 = 65194 kg kek The saturation temperature is 187.96 degC. ‘The exit temperature of the exhaust gas is therefore 197.96 degC, and the temperature CHANGE of the exhaust gas is -202.04 K. For the water at 20 degC from Table F.1, = 02963 Hi $1 kek ‘The turbine exhaust will be wet vapor steam. For sat. liquid and sat. vapor at the turbine exhaust pressure of 25 kPa, the best property values are found from Table F.1 by interpolation between 64 and 65 degC: 72.084 Hy = 2346.3. kg kg i WI 08932 Sy = 6.9391 kek : kek For isentropic expansion of steam in the turbine: S'3- Stig Ss: 8; : eee nae - avaeicsiy 83-6519 x3 = 0811 Hy = 2.17410 kg AH; == n-(H3 ~ Ha) Hy i= Ho + AHp3 Alig = ~437.964 2345x1094 kg ke H3 ~ Hig a= 83 = Siig + x3'Siy x3 = 0.883, Soca eR. 209Y 25. see (273.15 + 197.96):K For the exhaust gases: Ty = (273.15 + 400)-K Ty = 673.15K 12 = 47L11K McPH(673.15,471.11,3.34, 1.12:1073,0.0,0.0) = 3.9808 McPs(673.15.471.11,3.34,1.12-10 $,0.0,0.0) = 3.9741 MCPH = 9808 MCPS := 3.9741 molwe:= 1s 22 mol {To AH ggs °= R-MCPH-(T2 ~ T1) AS gas == R-MCPS: Hla 3k ‘AH gas = ~6.687 x 10° —— = -11.791 ae kmol ad kmoFK Energy balance on boiler: =ndot-AHgas mdot = ———_* mdot = 0.30971 £2. Ho —Hy sec (@) Wot := mdot-(H3 — Hz} Wadot = S135,65KW Ans. (b) By Eq. (5.25): To = 293.15-K Wabtideal ‘= ndot-AH gas + mdot-(H3 - Hj) 4 -Tar{ ndot-ASgag + mdot-(S3 — si)} _ Wit g Waotigeat Webtideal = -314.302kW 1 (©) For both the boiler and the turbine, Eq. (5.33) applies with Q 210Boiler: Ans, For the turbine: Sdotg = mdot(S3 ~ $2) Turbine: SEW! 1565 Ans. K w ; (@) Waotisoitr = 0453457 “Widjsnbsie = 192014 W Waottoserurbine = 0.1560-—— Woottostboiter ~ [Waotideal Fractionpoite Wdotiost turbine [Waoticeal| Fractionurbine ‘= Note that: ny + Fractionpjjer + Practionrurbine = 1 7.34 From Table F.2 for sat. vap. at 125 kPa: Hy = 2685.22 si = 72847 kg kgK For isentropic expansion, Sip = Sy = 7.2847 Interpolation in Table F.2 at 700 kPa for the enthalpy of steam with this entropy gives H 78H = 1 an = 46935982 n kg any Hy := Hy +H Wyss Ans. anInterpolation in Table F.2 at 700 kPa for the entropy of steam with this enthalpy gives mdot Wdot 7.35 Assume air an ideal gas. First find the temperature after isentropic compression from a combination of Eqs. (5.14) & (5.15) with C= 0. Then find the work (enthalpy change) of isentropic compression by a combination of Eqs. (4.2) and (4.7) with C=0. The actual work (enthalpy change) is found from Eq. (7.20). From this value, the actual temperature is found by a second application of the preceding equation, this time solving it for the temperature. The following veetors contain values for Parts (a) through (): 298.15, 101.33-kPa (375-kPa 353.15 375:kPa 1000-kPa Tye Le 100:kPa 500-kPa 373.15, 500-kPa 1300-kPa 299.82 14.7-psi 55-psi \s3e.71 S5.psi 135:psi 100 0.75 100 0.70 150} mot 0.80 50 | see 0.75 : 0.5-453.59 0.75 0.5-453.59 0.70, For the heat capacity of air: 0575-10 ° A=3355 B D := ~0.016-10°K? 0.5 (guess) 212Given AS= raw “fen + ea (: . I (e~1)- HF] Tau(To,Po,P) := Find(t) Ws Tau(To,.Po,,Pi) (451.06) 464.5 476.19 | oti | 486.87 | 434.74 (435.71 1cPH(298.15,431.06,3.355,0.575-10"?,0.0,-0.016:105) = 472.123 rcpH(353. 15 ,464.50, 3.355 ,0.575-10 ~,0.0,-0.016- 10°) = 398.669 1CPH(303.15, 476.19, 3.355,0.575-10" °,0.0,-0.016 105) = 617.403 1cPH(373 15,486.87, 3.355 ,0.575-10~ ,0.0,-0.016- 10°) = 408.647 ropti(299,82,434.74,3.355,0.575.107°,0.0,-0.016 10°) = 479.494 icpHi(338.71 ,435.71,3.385,0.575-1073,0.0,-0.016-105) = 345.980 472.123 ) (3925.2 398.669 | 3314.5 617.403 5133.1] J ICPH := K AH’ = R-ICPH AH'= _ 408.647 3397.5 | mol 479.494 3986.5 345.980 5233.6 (2876.5 te 4735 an := [SH 6416.41 3 7 AH = ae 4530 | mol 53154 41093 2137.36 T= 1S (guess) Given site n[ tol ye roel?) P(E) To Tau(To, AH) := Find(t) Gi Tau(To, AHI) ——> Wadbot := (ndot-AH) Ammonia: — Ty = 405.7-K Pore 1128bar = 0.253 To = 294.15-K Py = 200-kPa P= 1000kPa For the heat capacity of ammo 0.186-10°-K? Tro = 0.725 Tro Pro = 0.0177 Te Use generalized second-virial correlation: HRB(0.7250,0.0177,0.253) = —0.045843 0.045843 SRB(0.7250,,0.0177,0.253) = ~0.044781 SRBo := ~0.044781 The entropy change is given by Eq. (6.83) combined with Eq. (5.15); C= 0: Tis 14 (guess) SRB := 0.0 (starting value) 214Given AS= nls nta[naae t or ee) (r= 1)- (¢) . T = tau(SRB)-Tp T = 416.907K At the final P and this T, evaluate SRB: tT = Te) = 1.028 P, = 0.0887 ° SRB(1.0276, 0.0887 0.253) = ~0.069844 SRB := -0.069844 Iterate for T: T := tau(SRB)-Tp T = 423.094K T,(T) = 1.043 B( 1.0429, 0.0887 ,0.253) = -0.066701 SRB := -0.066701 tau(SRB):To T= 422814K T,(T) = 1.042 SRB(1.0422, 0.0887 ,0.253) = ~0,066841 SRB := ~0.066841 ‘T := tau(SRB)-To = 422.83K Te(T) = 1.0422 A further iteration is clearly not warranted. The enthalpy change for this final T is given by Eq. (6.82), with HRB at the above HRB(1.0422, 0.0887, 0.253) = -0.097461 0.097461 1cpHi(294.15,422.83,3.578,3.020-10" ?,0.0,-0.186-10°) = 580.487 ICPH == $80.487-K AH, sICPH AH’ := AHig + R-Te (HRB — HRBo) The actual enthalpy change from Eq. (7.17): AH aH = 56732. q mol n= 0.82 AH 218‘The actual final temperature Faq. (4.7), written: now found from Eq. (6.82) combined with 14 (guess) Given AHER Ato (s— 1) +B-10" + Ty (HRB - HRBo) Find(t) T := teu(HRB)-To T = 448.44K 1.1054, Iterate for final T: HRB(1.1054 , 0.0887 , 0.25: 0.085587 HRB := --0.085587 T = tau(HRB)-To T= 44745K Ty(T) = 1.1029 HRB(1.1029, 0.0887 0.253) = —0.086005 HRB := —0.086005 T := tau(HRB)-To T,(T) = 1.103 T =44748K Ans. SRB(1.1030,0.0887 0.253) = -0.056033 1.521 as , -2.168-1076,0.0) = 1.7134 ICPH := 636.059-K ICPS := 1.77134 AH := RICPH ait = 52882 mol P. as z= r{ 100s -tn| 22 as = 3201 (Pi molK Since the process is adiabatie: Sq = AS 221Ans, Ans. 72 Tl = G5+273.15)K TI = 308.15K ‘T2 := (200 + 273.15)K T2 = 473.15K Cp 3.5K v- RT ndot = 19.775 22 PL see With compression from the same initial conditions (P1,T1) to the same final conditions (P2,12) in each stage, the same efficiency in each stage, and the same power delivered to each stage, the applicable equations are: 1 P2) N where r is the pressure ratio in each stage and N is Pi) the aumber of stages.) Eq, (7.23) may be solved for T2prime: T2 :=[(T2-T1)-n +T1] 12 =4154K Eq. (7.18) written for a single stage is: RL pa \NCp T2=T1 (@ | Put in logarithmic form and solve for N: (a) Although any number of N’= 3.743 stages greater than this would serve, design for 4 stages. 2227.44 p2\N (b) Calculate r for 4stages: Nix 4 or (2) r Power requirement per stage follows from Eq. (7.22). In kW/stage: (©) Because the gas (ideal) leaving the intercooler and the gas entering the compressor are at the same temperature (308.15 K), there is no enthalpy change for the compressor/interehanger system, and the first law yields: Qdot, := -Weot, ‘Qdote = 975 Heat duty = 87.94 kW/interchanger (@) Energy balance on each interchanger (subscript w denotes water): With data for saturated liquid water from the steam tables: Aly = (1884-104. any = 83.642 kg kg {Qdot,| 7 mdotyy := (in each interchanger) ‘Aly R= 8314 464 6 35 347 5 25 12/455) P2=|6| Cp=l4s]R 505 8 55 496 7, 4.0, AH := [Cp-(T2~T1)] Ideal gases with constant heat capacities 223,Ans. 7.47 The following vectors con conditions first: 298.15 100-kPa. 363.15 200-kPa 333.15 |-K Py =| 20-kPa 294.26 L-atm 366.48, 15-psi '2000-kPa 0.75 fevers 0.70 5000-kPa n= |0.75 20atm 0.70 1500-psi 0.75 224 (7.22) AHs =| 4.745 x 10° (3.219% 108 3.729% 10° 3 5.959 10° 4.765 x 10° values for Parts (a) through (e). Intake 20-kg 30kg mdot :=} 15:kg }- 50-b 80-16 t sec. 257.2 6962) 523:1.4-—— 2173 714,3.From the steam tables for sat.liq. water at the initial temperature (heat capacity calculated from enthalpy values): 1.003 45 1.036} 420 V:=| 1017 eo 4.20 ek 1.002 4.185 1.038 (420 ByEq.(724) — AHs =[V-(P2 1.906 an v(i=een}(P2= i) By Eq. (7.25) AT := Cp (298.338) 363.957 T2:=(T1 +47) Tz =| 333.762 |K (367.986, 2257.48 Results from Example 7.10: i AH usr To i= 300K Wideat Since the process is adiabati Sq = AS Whost := To ASki 3622.7-—— 6.90! kg aK KD i 6.9485-—— 3529.6 ae cl ky a 3635.4-—~ 6.9875: kek 7 = 7 Mp? ki 2 ‘ 3475.6.— oats kg BTU STU .. 1507.0. BTU 16595 Ibm BIU TU a 1558.8. 222 1.6759. ere bm Sat. liq. and sat. vap. values from Tables F.2 and F.4 @ P3 = P4: i = 2584.82 332.4 tons e WI u 2609.95. 453 pare is ia H i i912 saan e Ene 2616.0 0644 ot 419.064= = Bru 11505.BTU 7 Se . tso17 se BTU BTU : 69.73.50 105.8. Tn 7 229Chapter 8 - Section A - Mathcad Solutions 8.1 With reference to Fig. 8.1, SI units, At point 2: Table F.2, Ha 8p == 6.9636 At point 4: Table Fl, Hg := At point 1: At point 3: Table Fil, Hig := Ha AB := 2382.9 x3 = 0.96 Hg i= Hiq+%sAHyy — H3 = 2496.9 Stig * AS = 7.3241 For isentropic expansion, $'3 = S2 83-8) x= la x33 = 0.855 ASiy [= Hig +X3AHy Hs = 2246 H3~ Ha Maubine = Fe $05. Ans Wy = Hs ~ Ha Qu ss Ha- Hy W, = -1.035x 10° Qu = 3.322 10° noce = Ha Ans a Qu 8.2 mdot:= 1.0 (kg/s) ‘The following property values are found by linear interpolation in Table F.1: State 1, Sat, Liquid at TH: HI = 60.7 Si 3482 PL State 2, Sat. Vapor at TH: H2 := 2792.0 S2:= 6.4139 P2 533 533 2ar83 State 3, Wet Vapor at TC: Hligq = 125 State 4, Wet Vapor at TC: Sli = 0.3929 (a) The pressures in kPa appear above. (b) Steps 2-3 and 4--1 (Fig, 8.2) are isentropic, for which $3=S2 and S1=S4, Thus by Eq. 6.73): 82-5) rte SS gear Svap — Sliq Svap - Sliq (©) The rate of heat addition, Step 1 Qdotl2 := mdot-(H2 - H1) (isis) (A) The rate of heat rejection, Step 3. H3 := Hliq + x3-(Hvap—Hliq) 4 := Hliq + x4-(Hvap — Hliq) HB = 1.919% 10° HA = 699.083 Qdot34 := mdot-(H4 - H3) (kS/s) (©) WdotI2 = 0 Wadot34 := 0 Waot23 := mdot(H3 ~ H2) t Wdot4] := mdot (HI - H4) Waoid = 161.6 Wdot23 + Weotdl | ¥ a ee 0.368 ee Qdotl2 | : Note that the first law is satisfied: ZQ = Qdotl2 + Qdot34. EW s= Wdot23 + Wdot4] TQ+IW=0 ‘The following veetors contain values for Parts (a) through (). Enthalpies and entropies for superheated vapor, Tables F.2 and F.4 @ P2 anc T2 (see Fig. 8.4): 280.6493 sisi kgK keK 0.8321. 7 9094.-K. kek kek i iw 0.6493-—— 8.1511-—— kek kgK | Syap = 1.3069. 73854 kek kek : ; o31a1-—BtU _ 1.756821 _ Tbpy-rankine mrankine 0.1326. — BTU 1.97812 Tbpyrankine Ibpyrankine em? 1.010-—— gm cm? 1.017 am 0.80 ( 0.75 ? 0.75 0.75 0.80 0.80 Manbine | 0.78 Mpume | 9.75 0.78 075 (oso, 0.75 2302 10000-kPa 10-kPa 100 7000-KPa 20kPa 1m | 5 8500-kPa. 10-kPa 1O-KW PL Pass 50 6500-kPa 101.33-kPa 30 950-psi 14.7-psi 80 (i2s-psi_) (psi Ha = Hig Hi = Ha+ Wpump — S2~Stiq S'3 = So x’ wap — Stig esaegeeeeLeaeaeeeeEeee Hy = [Ho + neubine:(H'3 ~ Ha) | See: wai mdot = ——~Set Wrurbine + Wpamp Qdoty Qdote = Qdot + Waot Answers follow: 240705) 395111 | ag sec 2318.4 ~ Qdoty Subscripts refer to Fig. 8.3. Saturated liquid at 50 kPa (point 4) om? KI Va == 1.030- Hq == 340.564-— am kg Saturated liquid and vapor at 50 kPa: ky Hiig := H. Hyap = 2646.0-— hig = Ha ” ie ki ky Stiq == 1.0912-— Syap = 7.5947-—— ig wk ap . : i By Eq. (7.24), Woump := Va-(P4-P1) Woump = 3.348 ie Hy = Ha+ Wpunp m=sa918 8 The following vectors give values for temperatures of 450, 550, and 650 degC: 3340.6 7.0373 Hp =| 3568.3 | So =| 7.3282 | EL kg kg-K 3792.9 7.5891 23285. 13 := Hig + x'3-(Hyap ~ Htig) S'3—Stiq ap ~ Stig Wrurbine = H'3 - Ho eee __ |Weurine + Wump| Qu = (H2- Hi) Qu (0.297 0314}: Ans. 0.532 Subscripts refer to Fig. 8.3. Saturated liquid at 30 kPa (point 4) as Va = 1.022 Hy s= 289.3022 am kg Saturated liquid and vapor at 30 kPa: . = 5000 Hig = Ha Hyap ‘= 2625.4 P4:=| 7500 |-kPa 10000. By Eq. (7.24), Hy = Ha + Wpump 294.381 296.936 2 299.491 } Hy = 23386 The following vectors give values for pressures of $000, 7500, and 10000 kPa at 600 degC 3664.5 7.2578 Hp =| 3643.7} So =| 7.0526 ae 3622.7 6.9013 $'3 = Sz H's == Hiig + 3-(Hyvap — Hi Hp- Hi) £5 (0.925 x3 =| 0.895 Aus. 0.873 From Table F.2 at 7000 kPa and 640 degC: Hy = 376642 $1 = 7.2200 82:58) kg kg-K For sat. lig. and sat. vap. at 20 kPa: ky Hlig i= 251.4532 Hyap = 2609.9-— kg kg ky Ky Sig = 0.6321 Svap = 7.9094 The following enthalpies are interpolated in Table F.2 at four values for intermediate pressure P2: 725 3023.9 750 3032.5 Pais “kPa u i TIS 3040.9 | kg 800, (3049.0 234n= 0.78 Wr = n-(H2-Hi) Hy +Wi2 -579.15 (38? 3) 7.4939) 572.442 | Ky 3194 | Ky 7.4898 | kd Wr= — F= — Se — 565.89 | ke 3200.5 | kz 74851 | kg-K (559.572, 3206.8, \TAT97, where the entropy values are by interpolation in Table F.2 at P2. S2~ Stig xy H’3 = Hiig + 8'3-(Hyap ~ Hi Syap~ Siig ao Was = n-(H3 ~ Ha) 20.817 -7811 | ky AW = Wi2- W23 AW= ne man 3.073 | ke 17.723 The work difference is essentially linear in P2, and we interpolate linearly to find the value of P2 for which the work difference is zero: timerp a ,P2,0.0| = 765.16kPa (P2) (a) Also needed are values of H2 and S2 at this pressure. Again we do linear interpolations: linterp(P2,H2,765.16-kPa) = 3197, oe Hp = 3197.9. 2 Z linterp(P2, 82, 765.16-kPa) = 7. 4369 Sp i= 7.4869. kek kg ‘We can now find the temperature at this state by interplation in Table F.2. ‘This gives an intermediate steam temperature 2 of 366.6 degC. 235‘The work calculations must be repeated for THIS case: So- Wio = H2-Hy eo Svap ~ Stig Wr = -s68.54 x3 = 0.94 kg = Hig + ¥3-(Hivap ~ Hig) kJ 2.469% 10° Waa = ~568.46— kg ks Work = Wiz + W23 Work = 1137 8 For a single fsentropie expansion from the initial pressure to the final pressure, which yields a wet exhaust: $1 - Sti x3 aaa Bs = Myig +¢3-(Hyap — Hig) wap ~ Stig ‘4 3k x3 = 0.903 Hy = 238% 10) Wis H3- Hy w= 1386.22 kg ‘Whence the overall efficiency is: Work i overall = 8202, Ans. He lh w 2368.7 From Table F.2 for steam at 4500 kPa and 500 degC: i J 3439.3. 8) = 7.031 kg . kg-K By interpolation at 380 kPa und this entropy, Fh n= 028 Hg = 2.918% 10° Isentropic expansion to 20 kPa: Sig = S2 Exhaust is wet: for sat. liq. & vap.: KI Hyiq == 251.453-— Hyap = 2609.9. zo kg kg WD Ky 0.8321. Svap = 7.9094. kgK 7 kek 237 Wi= (Hs - Ha) w= -sa.sseK keAig + x'4-(Hvap ~ Hig) Hy = 2317x10° ke 56x 10° H. af ke Vs-(P6~P. Wpump elt) Hg != Hs + Wpurap ks i Wamp = 5.841 = iis = 257.2947 For sat, lig, at 350 kPa (Table F.2): 24.270. ty kg We need the enthalpy of compressed liquid at point 1, where the pressure is 4500 kPa and the temperature is: Hy 38.87 (degC) 138.87 — 6 Thm (tr 273.15)-K ty = 15287 temperature, 132.87 degC ferpotation in Table F.1 gives: 3 559.5. Psat = 294.26-kPa Veatstig i= 1.073 kg gm Heattig Also by approximation, the definition of the volume expansivity yields: Pr: Po 1 (soto om Veatlig 20 J gmK p=932x 104+ 23888 By Eq. (7.25), KI Hy = Hoattig + Vsattig(1-B-T1)(P1—Psat) Hi = 561 305 By an energy balance on the feedwater heater: 1-H H3— Hz mass «mass =0,13028kg Ans. Work in 2nd section of turbine: Wir = (ekg — mass)-(H4~ Hs) Wh = ~307.567k) Wret °= (i+ Wpamp)I-kg + Wir Wret = ~823.3K) Que: (Ho ~ Hi)-1-ke W, . Qu = 2878kI ns [Wn n= 0.2861 Ans. Qu Refer to figure in preceding problem. Although entropy values are not needed for most points in the process, they are recorded here for future use in Problem 15.8. From Table F.4 for steam at 650(psia) & 900 degF: Hp = 1461.22 Ibm, By interpolation at S0(psia) and this entropy, BIU Hs = 1180.4-—— Wi:= n-(H'3 - He) m Hg i= H+ Wy = 12422810 ~219.0420U Ibm bm BIU, 83:5 1.7431. - Tb, Tankine Isentropic expansion fo 1(psia) Exhaust is wet: for sat. lig. & vap.: BTU Hg #= 69.73-— Hyap 11053228 Ibm Sm 239BTU 0.1326-————__ Ibryrankine Hy +n-(H4~ Ha) Hy - Hiig yap — Hig x4 = 0.944 Ps = I-psi Vs(P6 - Ps) Woump == ‘pump 650:psi For sat. lig. at S0(psia) (Table F.4): Hy = 250.21 220 Ibm BTU Syap = 1.9781-———_—_— a Ibe rankine Aig + X4(Hyap ~ Hig) 31.204 BEL tom Hg = 1097957 $4 := Stig + X4:(Svap ~ Stig) Sq = 1.874g—BU_ Ib rankine 3 # Vii V5 = 0.0161-— Hig. 3 Ibm BTU Woump = 2.489 cae I Ho = Hs + Wpump He = raise ty := 281.01 S87 == 0.4112. em Toy tankine We need the enthalpy of compressed liquid at point 1, where the pressure is {650(psia) and the temperature is ty = 281.01-11 Ty (t1 +459.67)-rankine ty = 270.01 At this temperature, 270.01 degF, interpolation in Table ¥.3 gives: Poot = 41.87-psi Bru 238,96-—— ; bn BrU Hes 240of the volume expansivity yields: (cotmsootre) a ———— |———_ _ Piss Veattiq 20 7) Tone rankine B= 495 10° J rankine By Eq. (7.25) and (7.26), , BTU Hy = Hsatiiq + Vsataig:(1 - B°T1)-(P1 ~ Psat) Hy = 257.65 — BTU S81 == Ssatliq + Vsat.ig’B-(P1 Ps. S} = 0.397-———_—_ 1 liq + Vsat.tig'B-(Pi = Psat) 1 iaankne By an energy balance on the feedwater heater: H) - He See ret Ey tte ‘mass =0-18687 Ibm, Ans. Work in 2nd section of turbine: War: (I-lbm— mass)-(Hg ~ H3) Wy = -158.051 BTU Wret = (Wi+ Wpump)1+Ibm + War Wret = -374.586BTU Qu = 1.204% 10°BTU 24189 Turbine Steam at 6500 kPa & 600 degC (point 2) Table F. Hy = 365212 Spi= 7.1258 Pp := 6500-KPa kg kgK AC point 3 the pressure must be such that the steam has a condensation Aemperature in feedwater heater 1 of 195 degC, 5 deg higher than the temperature of the feed water to the boiler at point 1. Its saturation pressure, corresponding to 195 degC, from Table F.1, is 1399.0 kPa. The steam at point 3 is superheated vapor at this pressure, and if expansion from P2 to P3 is isentropic, ky His := 3142.6— Wy:= n-(H3 -H: 3 ig i= n-(H3— Ha) kK = Ho + Wy Hy = 3.244 1 Wy = ~407.6= kg kg From Table F. Hyo = 8290-4 kg Simitar eal lations are required for feedwater heater I 242,At the exhaust conditions of 20 kPa, the properties of sat. liq. and sat. vap. are: KI ’ jig = 251.453-— Viig = 1.017-—— hig ke bg em kr § = 0.8321-—— Sig = 08321 we find 17, then 18 is the mid-temperature hetween t7 and t(190 degC), and ‘that fixes the pressure of stream 4 so that its saturation temperature is 5 degC hhigher. At point 6, we have saturated liquid at 20 kPa, and its properties from Table F.2 are: ‘sat +273.15)K Vo := Vig Ikq. 7.24) KI Wpanp = 8.238 — AHg7 *= Wpump ‘B We apply Eq, (7.25) for the calculation of the temperature change from point 6 to point 7. For this we need values ofthe heat capacity and volume expa of water at about 60 degC. They can be estimated from data in Table F. ., . 272.0-2302 kd Cp i= ar 10 kg-K —4 1 B= 5.408 10° 4 cp = 41s K kek Solving Fg. (7.25) for delta T gives: AH67 ~ Viig-(1 ~ B-Tsai)-(P2~ Po) ATs San aeg ee rae ATg7 = 0.678K ATe7 190 -t7 cat + tors + to+5 17 = 60.768 243tg = 130.38 From Table F.1: Hg ss 54797 2 Hy = Hyig + AH67 ty = 125.38 To 2= (273.15 +t9)-K kr Hy = 259.691 — kg Atpoints 9 and 1, the streams are compressed liquid (P=6500 kPa), and we find the effect of pressure on the liquid by Eq. (7.25). Values by interpolation in Table Fl xt saturation temperatures 19 and f1: om? Veat9 = 1.065-- gm mm Vogt) = 1.142 Pyatst = 1255.1-kPa. em om om? AVg = (1.075 — 1.056)-—— AV, = (1.156 ~ 1.128) em em 1 AVo 1 4v, Bo Tao aT Voat AT et —31 = 892x104 = 1.226% 103 Bo z Bi 7 KI Ho = Hsa.9 + Vsat9-(1 ~ Bor Ts){(P2 ~ Psat.9) Hy = 530.97 Ty 273.15 + 190)-K T) = 463.15K AS Hy := Hg, V. 1-By-Ty)}-(P2—Poat Hy = 810.089— 1 = Hgaa.1 + Vsat.i-(1 ~ Br T1)(P2~Psat.t) 1 = Now we can make an energy balance on feedwater heater Ito find the ‘mass of steam condensed: Hy) - Ho my = — H3 — Hig O.11563Kg Ans. 24a‘The temperature at point 8, #8 = 130.38 (see above) is the saturation temperture in feedwater heater II. The saturation pressure by interpolation in Table F.1 is 273.28 kPa. Isentropic expansion of stcam from the initial conditions to this pressure results in a slightly superheated vapor, for which by double interpolation in Table F.2: Then Hg = Ho + 9-(H's — Ha) oat x 10 kg ‘We can now make an energy balance on feedwater heater II to find the mass of steam condensed: Hy = (Hy = Hy)-1-kg ~ my (Hip - Hs) Ha- Ag ii’ 0.09971 Kg Ans. my c= ‘The final stage of expansion in the turbine is to 20 kPa, where the exhaust is wet. For isentropic expansion, i S82-Stiq xsi5 Hig + ¥'5-(Hyap ~ Hig) ‘ap ~ Stiq x'5 = 0.889 2349.10 ke ‘Then Hy = Ho + n-(H's — Ha) The work of the turbine is: Weurbine = Wy-I-kg + (1-kg — my). (Hg - Hg)... +(1-kg ~ my~ my)-(Hs— Ha) Wrarbine = -936.2kI Qu (H2-Fi}rke Qu = 2.842« 105g /Wrurbine + Wpump' Ike} 32¢ ns. tH aM 248,810 Isobutane: Te 8.1K Pe = 36.48: bar 0.181 For isentropic expansion in the turbine, let the initial state be represented by symbols with subscript zero and the final state by symbols with no subseript. Then To = 533.15K Po J 800-kKPa P= 450-kPa As For the heat capacity of isobutane: morK 6 Azle B ass 10" To Po Tos Tro = 1.3064 Pro = = Pro = 1.3158 w= 0 0=B 0 Use generalized second-virial correlation: HRB(1.3064, 1.3158,0.181) = -0.868161 HRBo := -0.868161 SRB( 1.3064, 1.3158,0.181) = ~0.486134 SRBp := -0.486134 ‘The entropy chang: given by Eq, (6.83) combined with Eq. (5.15) with D T= 0.8 (guess) SRB := 0.0 (starting value) Given r y 26 P AS = RL A-tn(s) +] BT + C-T02| E*4) |e —1) nf 2), L a) Po) _+SRB- SRB tau(SRB) := Find(z) T := tau(SRB)-To T= 452.5K At the final P and this, evaluate SRB: T P = T,(T) = 1.1088 Pes Py = 0.1234 Te Pe SRB(J_1088 , 0.1234,0.181) = ~0.073105 SRB := ~0.073105 T = tau(SRB)-To T = 454.52K TT) = 11137 Although it will make little difference, we now recalculate SRB at this femperature: SRB(1.1137,0.1234,0.181) = -0,072162 SRB = ~0.072162 T == tau(SRB)-To T = 454.49K TT) = 137 246A further iteration is clearly not warranted. ‘The enthalpy change for this final temperatu the above T: given by Eq. (6.82), with HIRB at HRB(1.1137,0.1234,0.181) = -0.113300 HRB := -0,113300 repHi{s33.15,454.48, 1.677,37.853:1073,-11.945-107 60.0) = -1372.822 5 1372.822-K Abig := RICPH — AHig = -1.141x 10° 1cPH mol AB turbine “= AHig + R-Te(HRB ~ HRBo) J AHturbine = ~8852.4—— Wrurbine # AHourbin mol ‘urine ‘The work of the pump is given by Eq, (7.24), and for this we need an estimate of the molar volume of isobutane as a saturated liquid at 450 kPa. This is given by Eq. (3.63), The saturation temperature at 450 kPa is given by the Antoine ‘equation solved for t degC: VP := 450-kPa_ Ayp = 1457100 Byp = 2606.775 — Cyp s= 274.068 Byp i ts v = = (t+ fe i: t=34 T= (14273.15)-K kPa T= 30715K cm’? Vo = 262.7 0.753 mol 02857 3 it) Vig» ver a Vig = 112.36 mol Wopump = Viig:(Po - P) a z ipamp *= Viig-(Po Woump = 488.8— mol The low rate of isobutane can now be found: ee 1000-kW ce [Weurbine + W pum] 247‘The enthalpy change of the isobutane in the cooler/condenser is calculated in two steps: a. Cooling of the vapor from 484.48 to 307.15 K b. Condensation of the vapor at 307.15 K Enthalpy change of cooling: HRB at the initial state has already been caleulated. For saturated vapor at 307.15 K: aus T, = 0.7526 Te HRB(0,7526, 0.1234, 0.181) = ~0.265848 ARBsat := ~0.265848 1ePH454.48, 307.15, 1.677,37.853-107§, 11,945.10" 6,0.0) = ~2112.435 ICPH := ~2112.435-K Abiig := RAICPHL Alig = 1.756% it mol AH, = AHig + R-Te(HIRBygi ~ HRB) ‘AH, = ~18080 For the condensation process, we estimate the latent heat by Eqs. (4.12) and (4.13): Tq = 261.4K Tn = 0.641 ( (Pe RT 1.092 inf =) = 1.013 ; AH == SPs Ay = 2.118 10*§ > 0.930 = Tm mol J AH, AH, = -18378—— mol Qdotout := mdot (AH, + AHp) 1000-kW Qdotin = |Weurhine + Wpumg| mdot + |Qdoto, — [Weursine + Wpume] | Qdotou] Span Qdotou, = =4359KW Qdotin' = 5359kW Ans. 248,8.11 Isobutane: T, := 408.14K. Po 15.36.48: bar o = 0.181 For isentropic expansion in the turbine, let the initial (inlet) state be represented by symbols with subscript zero and the final (exit) state by symbols with no subscript. Then 3400-kKPa P= 450-kPa— molwt = For the heat capacity of isobutane: pp ew 37.853:10 1.945.107 K Po Tyo = 1.0124 Pome Pro = 0.932 Use Lee/Kesler correlation for turbine-inlet state, designating values by HRLK and SRLK: HRLKo := ~1.530 SRLKo = -1.160 ‘The entropy change is given by Eq. (6.83) combined with Eq. (5.15) with D = 0 t= 0.8 (guess) SRB = 0.0 (starting value) Given 14+1)] AS=R AnG)4[ ey ror? a | (c-1)-wof 2) 2), Po, +SRB~SRLKo tau(SRB) := Find(t) T := tau(SRB)-To 329.31K At the final P and this T, evaluate SRB: T THE) = TCT) = 0.8069 Py = 0.1234 SRB(0.8069, 0.1234,0.181) = -0.19472 SRB := ~0,19472 T = tau(SRB)-To T= 33431K THT) = 0.8192 Although it will make little difference, we now recalculate SRB at this temperature: ‘SRB(0.8192, 0.1234,0.181) = -0.18538 SRB := ~0.18538 T= tau(SRB)-Tp T = 334.07K Ty(1) = 0.8186 249A further iteration is hardly warranted. The enthalpy change for this final temperature is given by Eq. (6.82), with HRB at the above T: HRB(0.8186, 0.1234 0.181) = -0.21941 HRI 0.21941 3 1cpH(413.15,334.07, 1.677,37.853:10" 3, -11.945-107§,0.0) = —1118.642 ICPH s= ~1118.642-K AHigi= RICPH Hig = -9.3x ws mol Abiurbine ‘= AHig + R-Te(HRB - HRLKo) J Alyurbing = ~4853.6— Wrurbine = AH turbine mol The work of the pump is giv molar volume of saturated- calculated in Problem 8.10: Eq. (7.24), and the required value for the isobutane at 450 kPa (34 degC) is the value J Wy = Viiq (Po - P, W, = 331.462 — pamp= Vig (POP) Wyamp = 3814625 For the cycle the net power OUTPUT is: 75 KS Waot z= -mdot (Warne + W pump) Wedot = 5835KW Ans. The enthalpy change of the isobutane in the cooler/eondenser is calculated in ‘two steps: a, Cooling of the vapor from 334,07 to 307.15 K b, Condensation of the vapor at 307.15 K Enthalpy change of cooling: HRB at the initial state has already been calculated. For saturated vapor at 307.15 K it was found in Problem 8.10 as: HRBgat = -0.2658 icphi(334.07,307.15, 1.677,37.853-10",-11.945-10" §,0.0) = 338.775 ICPH := ~338.775-K AHig = R-ICPH AHig = -2817 4 mol AHg := AHjg + R-Te(HRBsa ~ HRB) 250For the condensation process, the enthalpy change was found in Problem 8.10: ‘AH = -18378- Qdotout := mdot-(AF, + AHp) Qdotou = -27552KW Ans. For the heater/boiler: Qdotin = Waot + |Qdotoutl ‘Qdotin = 33387KW Ans. Weot ge — FONTS. Ans. Qdotin thet ‘We now recalculate results for a cycle for which the turbine and pump each have an efficiency of 0.8. The work of the turbine is 80% of the value calculated above, ie, Wiurbine := 0.8 Wrurbine Wiarbine = ~3883— mol ‘The work of the pump Wpump J Wopump = Wamp = 414.3— aa 8 mol Waot := -mdot(W'turbine + W'pamp) - Wedot =-4476KW Ans, The decrease in the work output of the turbine shows up as an increase in the heat transferred out of the cooler condenser. Thus Qdotout = Qdotout + (Wrurbine~ Wrurbine)-mdot Ans. The increase in pump work shows up as a decrease in the heat added in the heater/boiler. Thus Qdotin = Qdotin~(Wump— Wpump}-mdot Qt, = 33280kW. Ans, Wdot Qdotin 258.13 Refer to Fig. 8.10. 8d Pe := I-bar Pp := 5-bar a By Eg. 8.290): = Vo (Pp)" Ne ¥o) Ans Vo \Pe} Eq. G.29b): Qpa = 1500-500" mol Qpa = Cp{Ta Ta = 515.845K Ratio Tue cy 9 Ans. 2528.16 heating . (combustion) P (par) A cooling v Figure shows the air-standard turbojet power plant on a PV diagram. Ta := 303.15-K Te = 1373.15-K By Eq. (7.22) a (pp)? 3 Wan= Cp-Ta||[—= | -1] = Cp-Ta-ler? 1) (Pa) R G 2 Pp)" 7 Wen ® CeTe}]— | - 1} © Cp-Teler? = 1 Pe, where cr is the compression ratio and er is the expansion ratio. Since the two work terms are equal but of opposite signs, 5 (guess) (3 ) 62) i 2 7 Given Toler” — 1) = -Taler 1) er = Find(er) er = 0.552 253,cp (7.18): Tp2 Te! (7.18); D of ) By Ee This may be written: Tp := Te-er TSbar y= 0.8 817 Ta:=305-K = Pass LOSbar Py Assume air to be an ideal gas with mean heat capacity (final temperature by iteration): McpHi(298.15,582,3.385, 0.575.10" 3,0.0,-0.016-109) = 3.5998 Cimgir = 3.5998-R Cpr = 29.929 —— 254Compressor: fr _R Comayts |( Pp) 5 Wai 22 | 1) Woyie = 8291 10°§ 7 IPa mol Tate tp = 582.009K Tass 7 B At Comair B Combustion: CH4+202=C0O2+2H20 Basis: Complete combustion of 1 mol CH4. Reactants are N mol of air and Imol CH4, Because the combustion is adiabatic, the basie equation is: AH + AHy98 + AHp = 0 For AH_R, the mean heat capacities for air and methane are required. ‘The value for air is given above. For methane the temperature change is very small; use the Value given in Table C.1 for 298 K: 427 R. The solution process requires iteration for N. Assume a value for N until the above energy balance is satisfied. @) Te Aly = Cpmgie-N-(298.15 = 582.03)-K + 4.217-R-(298.15 — 300)-K 1000K oN 7.638 (This is the final value after iteration) AHp = ~4.898 x 10° mol The product stream contains: 1 mol CO2, 2mol H20, 0.79N mol N2, and (0.21N-2) mol 02 (oa 5.457 1.045 L137 3.470 1.450 0121 | -10 10° 3.280 0.593 0.040 3.639, 0.506 0.227, 2558.638 A: Yai B > A= 198517 B= 0.036 D B,D yw ~1.387% 10° Mcphi(298.15, 1000.,198.517,0.0361 ,0.0,-1.3872-10°) = 221.483338 Cpmp = 221.4833-R AHp := Cpmp:(To - 298. 15K) AHp = 1.292 10° mol From Ex. 4. Hao = -802625 mol AH + AH29g + AHp = 3. os (This result is sufficiently close to zero.) mol Thus, N = 57.638 moled Of aif per miole of methane fadk “Ans. Assume expansion of the combustion products in the turbine is to 1(atm), iLe., to 1.0133 bar: Pp = 1.0133bar Po = 7.Sbar The pertinent equations are analogous to those for the compressor, ‘The mean heat capacity is that of the combustion gases, and depends on the temperature of the exhaust gases from the turbine, which must therefore be found by iteration, For an initial calculation use the mean heat capacity already determined. This calculation yields an exhaust temperature of about 390K. Thus iteration starts with this value. Parameters A, B, and D have the final values determined above. mcpti( 100,343.12, 198.517, 0.0361 ,0.0,1.3872-105) = 222.356026 Cpm := 222.356-R For 58.638 moles of combustion product: one 58.638-CpmT see Ws astonty| 2] : ws = 1.214% 10° ” LVPe, mol Ws . To:=Tet Gm Tp 2343123K° (Final result of iteration.) Ans, nl 256Wane = WS + W5aieN (J per mole of methane) Parts (b) and (¢) are solved in exactly the same way, with the following results: ()) Te = 1200 N= 3748 Winet = -7.365:10° Ty = 343.123 7519-10° Tp = 598.94 (©) Te 1500 N= 24.07 Wepet = 287Chapter 9 - Section A - Mathcad Solutions 92 TH (204.273.15)K 293.15K S3.15K, To = (-20+273.15)K Tc Odore := 1250002. day Te Scam = 03) 0 0.6-0¢anot dot BNE 9.2) Wot = 0.381 kW ° twat Cost = 267183583 ns, . ° 9.4 Basis: 1 Ibm of tetrafluoroethane The following property values are found from Table 9.1: 0.09142 State 1, Sat. Liquid at TH: HI := 44.943 $1 State 2, Sat. Vapor at TH: H2 := 116.166 $2 » State 3, Wet Vapor at TC: Hliq := 15.187 Hvap := 104.471 iq := 0.03408 Svap := 0.22418 P4 (a) The pressures in (psia) appear above. (b) Steps 3-2 and 1-4 ( Thus by Eq. 6.7: State 4, Wet Vapor at TC: ig. 8.2) are isentropic, for which $3=S2 and S1=S4 — Siig Svap— Sliq 971 (©) Heat addition, Step 4 HB := Hliq+33-(Hvap—Hlig) 4 <= Hig + x4-(Hvap — Hlig) H3 = 101.888 H4 = 42.118 Q43 := (H3 - Ha) 043 = $9.77 (Bau, 258(d) Heat rejection, Step 2-1: Qai = (HI -H2) (Bru/lb,,) © Wiss 0 W32 := (H2 - 13) Wi4:= (H4-HI) 43 oe a. W14 + W32 a= $219 Note that the first law is satisfied: 2Q = Q21 +.Q43 EW i= W324 Wid TQeEW=0 Te = 298.15-K Ty = 523.15:K (Engine) Te = 273.15-K ‘Ty = 298.15:K (Refrigerator) Te By Eq. (5.8): x u Ncamot = 0.43 By Eq. (9.3): By definition: But Whence Quy Given that: 4) = 0.6-NCamoe Qc Qu= 269(a) Qc mk Ws 1LSkW see ee © 5 2.667- Ans. Ww . Ans. ©) Qu = Qc+W Qu ee (© oF Ty = (40+273.15)K Ty = 313.15K Ta-Te o \ To := Ti ; | Fe = 227.75K Ans. ori) - or -45.4 degC ‘The following vectors contain data for parts (a) through (e). Subseripts refer to Fig. 9.1. Values of H2 and S2 for saturated vapor come from Table 9.1. (489.67 0.79 600 479.67 0.78 500 469.67 |-rankine y=) 0.77 Qdote =| 400 Be 459.67 | 0.76 300 a 449.67, (0.75 200, 107.320 0.22244) 105.907 0.22325 H =| 104.471 | BY s2=| 022418 |B I Top tankine 103.015 0.22525. 101.542 tase From Table 9.1 : Bu Ty s= $39.67: rankine Hyg = 37.978. — for st. liquid Tom S528) (isentropic compression) 260‘The saturation pressure at Point 4 from Table 91 is 101.37(psia). For isentropic compression, from Point 2 to Point 3', we must read values for the enthalpy at Point 3° from Fig, G.2 at this pressure and at the entropy values $2. This eannot be done with much accuracy. The most satisfactory procedure is probably to read an enthalpy at S~0.22 (H=114) and at S=0.24 (H#=126) and interpolate linearly for intermediate values of H, This leads to the following values (rounded to 1 decimal): 115.5 116.0 nes Be Hg s= Ha + AHy3 bee 1 1172 Hy = Hy TERE (24.084) 273.711 30,098 276.438 KW k Hy = 883372 V3 =|36337 (© ty =| 279.336 | kg kg kg 43.414 283.026 50.732. 286.918, — mdot := xtc Ans. = aon Ans. Qdoty Ans, ——> Wdot := (mdot-AH3) Ans, 261Qdote Wdot ©Camot Ans. Subscripts in the following refer to Fig. 9.1. All property values come from Tables F.1 and F.2. Tp = (44273 15)-K 14 = G44273.15)-K 11 = 0.76 Qdote 1200. Hp = 2508.94 sp = 9.0526 4. sec kg kek kr : ; Hae 2.4 (isentropic compression) The saturation pressure at Point 4 from Table F.1 is 5.318 kPa. We must find in Table F.2 the enthalpy (Point 3') at this pressure and at the entropy S2. This requires double interpolation. The pressure lies between entries for pressures of J and 10 kPa, and linear interpolation, with P is unsatisfactory, Steam is here very nearly an ideal gas, for which the entropy is linear in the logarithm of P, and interpolation must be in accord with this relation. The enthalpy, on the other hand, changes very little with P and can be interpolated linearly. Linear interpolation with temperture is satisfactory in either case. ‘The result of interpolation is Hy - Hi wy = 28147- AHo3 : Hy = Ha kg a Hos = 402.368 2 bs ie 26291 3k Hy == Ho + AHos Hy = 2911x107 KE ns, see mdot= 0: it Qdotjy := mdot-(H4- H3) Qdoty = <1404 = Ans. Weot = 204kW Ans. ow Sete 55,881 Ans. Wdot sae rae canst 39238 Ans. amet 'T4-T2 seria ~ Parts (a) & (b): subscripts refer to Fig. 9.1 5 (Btuy(s) At the conditions of Point 2 {1 P = 14.667(psia)} for sat. liqui 5 degF and and sat. vapor from Table 9.1: Btu Btu 505 Hyap = 100.799" Hy = Hyap ibm bn Hig 2= 283Bu Btu Stig = 0.01733 = 0.22714. ig Tbprrankine Svap 7 Tprrankine For sat, liquid at Point 4 (80 deg): Bu Bu Ha := 37.9782 S4:= 0.07892. ‘ ibm ibmrankine (a) Isenthaipic expansion: Hy := Hy Buu Qdote aes dot — mdot 0.0; Ans. Qin 5 Ho-Hi os (b) Isentropie expansion: Si=S4 BTU Hhig + x1-(Hyap— Hig) Hi = as (©) The sat. vapor from the evaporator is superheated in the heat exchanger to 70 degF at a pressure of 14.667(psia). Property values for this state are read (with considerable uncertainty) from Fig. G.2: 75-3 Thin Qdote Hoa - Ha (@)_ For isentropic compression of the sat. vapor at Point 2, S3 = Syap and from Fig. G.2 at this entropy and P=101.37(psia) 1133-2 Eq. (9.4) may now be Ibm applied to the two cases: In the first case Fi1 has the value of Hd: Hg Hp - Hy H3 HpIn the second case H1 has its last calculated value [Part (b)]: Hy) He 3:7659° Ans. In Part (c), compression is at constant entropy of 0.262 to the final pressure. Again from Fig, G.2t Bu ie (Last caleulated H3 := 138 ca Wot := (H3 - H2,)-mdot value of mdon) Wdot = 1.289 ou see dot y= Jeote| 31871 Ans. Waot se 9.12 Subscripts: see figure of the preceding problem. ‘At the conditions of Point 2 [sat. vapor, t = 20 degF and P = 33.110(psia)] from Table 9.1: Btu Buu Hi := 105.907 $y = 0.22325-—B 7 om 7 Ibgrankine At Point 2A we have a superheated vapor at the same pressure and at 70 degF. From Fig. G.2: Bu Bu Hoa = 116-2 Spq = 0.2435. 1 fbn ae Ibjetankine For sat. liquid at Point 4 (80 degF): Br Ha = 37.9782 Sa = 0.078922 Thm nt Energy balance, heat exchanger: Hy = Hy~ Haq +H H = 2788550 Qdote Ibm mdot = 25.634— H2-Hr sec mdot9.13 For compression at constant entropy of 0.2435 to the final pressure of 101.37(psia), by Fig. G.2: Bu H3—H2a Hy = 127-—— AH om, tm a n Bru Woot := mdot-AH comp AHoomp = 14.6677 — m 396.66KW Ans. If the heat exchanger is omitted, then H = H4. Points 2A & 2 coincide, and compression is at a constant entropy of 0.22325 to P= 101.37(psia). Qdate mdot Ho -Ha Btu Weot := mdot-AHeomp AHlcomp = 1345755 ila Bp mdot = 29.443 =—= = 4i8.032kW Ans, Subscripts refer to Fig. 9.1. At Point 2 [sat. vapor @ 10 degk] from Table 9. Ho= rosa 2 = 022418 BY S2 H values for sat. liquid at Point 4 come from Table 9.1 and H values for Point 3° come from Fig. G.2. The veetors following give values for condensation temperatures of 60, 80, & 100 degF at pressures of 72.087, 101.37, & 138.83(psia) respectively. 31.239 1133 Bu tu Hy =] 37.978 | Wy s=] 1168 aa Hy = Hg 44.943) ™ n93)™ 266(@) By Eq. (9.4): a ‘Ans. an = BoB Si AH = H3-H; = ince = H- ») OTs 3 — Ho Eq. (9.4) now becomes —> -H paar ‘Ans. AH 9.14 WINTER Ty = 293.15 WINTER Waot := 1.5 Qdoty = -0.75-(TH- Te) House : Ty 7293.15 K iQui Wdor_ _ Ta-Te [Qdots] Ta Te :=250 (Guess) Given Wdot Tu-Te 267SUMMER Te = 298.15 SUMMER Qdote == 0.75-(Ty = Fc) Wdot _ TH-Te Qaote c Tu i= 300 (Guess) Given, Weer _ Ta~Te 0.75-(TH-To) Te Ty := Find(T 4) House 293.15 K Maximum t= 49.42 degC 9,15 and 9,16 Data in the following vectors for Pbs. 9.15 and 9.16 come from Perry's Handbook, 7th ed. 1033.5 1186.7 fe. bck Ho := 284.7. = His = ey 785: kj 1056.4) kg By Eq. (9.8): 2 ly Eq. (9.8): 0351 0.17 ) Ans. 9.17 Advertized combination unit: TH == (150+ 459,67)-rankine Te := (30 + 459.67)-rankine ‘Ty = 609.67 rankine Te = 489.67 rankine Btu Ta-Te Btu Weasnot = 12253— $= 50000. Weamot '= Qc Qc te ‘Camot ‘= Qc" Tc " 2689.18 919 Bu S:Weamot Wi = 18380 Wis This is the TOTAL power requirement for the advertized combination unit. ‘The amount of heat rejected at the higher temperature of 150 degF is Btu Qu = Wr+ Qe Qu = 683805" For the conventional water heater, this amount of energy must be supplied by resistance heating, which requires power in this amount. For the conventional cooling unit, Ty = (120 + 459.67)-rankine Bi Weamot = QC Wow = 919052 Work := 1.5-Weamot Work = is7ss St t The total power required is Wit = Qu + Work i ee NO CONTEST To := 210 Te = 255 Ty := 305 By Eq. (9.3): c ‘c oy #= 0.65: oy = 0.65. Ty-Te 7 Ta-Te Qe wie ce 1 on Define r as the ratio of the actual work, WI+ WIL, to the Carnot work: This problem is just 2 reworking of Example 9.3 with different values of x. It could be useful as a group project, i 269Chapter 10 - Section A - Mathcad Solutions 10.1 Benzene: Ay i= 13.8594 By == 2773.78 Cy = 220.07 Toluene: Ag = 14.0098 By = 3103.01 C2 = 219.79 BL Bo AH Ap nas i Psaty(T) =e 8 - KPa Psatp(T) :=€ kPa (a) Given: xj = 0.33 T:= 100-deg@ Guess: yy := 0.5 P= 100-kPa Given xj-Psaty(T) +(1- x1)-Psatg(T) = xy-Psaty(T) = y-P Find(y, ,P) y= 0545 Ans. B=109.119kPa Ans. (b) Given: OO-degC Guess: xy := 0.33 P= 100-KPa Given xy-Psat) (T) + (1 —x1)-Psatg(T) = xyPsaty(T) = y-P XL := Find(xy ,P) () (oF) (© Given: x) Ans. P= 92,042kPa Ans. 0.33 P= 120-kPa Guess: yj i= 0.5 T (00-degC Given xy-Psaty(T) +(1 —xy)-Psatg(T) = P xr-Psaty(T) = yP ind(v1,1) Ans, ‘T's 103,362dekC Ans.(@) Given: yy 33 P= 120-kPa Guess: xy 100-dege Given xp-Psaty(T) + (I~ x1}-Psatg(T) = P xp-Psaty(T) = ypP (x1) x . { : | = Find(xy ,T) Xp=0.173. Ans. T= 1090.161degC Ans. TT) i (©) Given: l0S-degC P := 120:kPa Guess: xj = 0.33 yy = 0.5 Given xp-Psaty(T) + (1 —x1)-Psatg(T) = P xy-Psaty(T) = ypP Find(xy.y1) 3} =0383° Ams. 20.485 Ans. oO 2 = 0.33 x1 = 0.283 yi = 0.485 Guess: L:=035 Vir0s Given 22 Lx t Ve L+Vel ind(L,V) Vapor Fraction: = =.0.93] Ans. (i ()- (g) Benzene and toluene are both non-polar and similar in shape and size. Therefore one would expect little chemical interaction between the components. The temperature is high enough and pressure low enough to expect ideal behavior. Liguid Fraction: 1, = 0.769. Ans. Fa]10.2 Pressures in kPa; temperatures in degC (a) Antoine coefficients: Benzene=1; Ethylbenzene=2 3.8594 By = 2773.78 Cy == 220.07 4.0045 Bp = 3279.47 C2 = 213.20 Psat) (T) Aye] sat (T) := exp] Ay — a (7) PAI — a qi) Psatz(T) := exp} A2 - — oe P-x-y diagram: = T= 90 P(x1) s= xy-Psaty(T) + (1 —x))-Psat(T) T-x-y diagram: — P' := 90 ‘Guess t for root function: t := 90 1(xp) == root{_x1-Psaty (t) + (1 — x1)-Psata(t) - Pi] Xy-Psaty(T(x;)) Bani) e Uw) Bastia) x1 3= 0,0.05..1.0 ts 140 130 120 ho no os 1 5 05 1 xtyi(u) xryi(s) 272(b) Antoine coefficients: 1-Chlorobutane=1; Chlorobenzene-2 Ay == 13,9600 C1 C2 Ag = 13.9926 = xy Psat (T) + (1 —x4)-Psata(1) ‘T-x-y diagram: —P':= 90. Guess t for root function: t := 90 T(x) = root] xy-Psaty(t) + (1 x1)-Psatgit) ~ P’,t] xa Psat (T(x) beats Gey)) (xy) Psaty 0,0.05..1.0 (rs) 160 11333) P(x) P(x) 66.67 | 20 05 | 0 05 1 xtoyu(xa) x1 ¥ihs) 27310.3 Pressures in kPa; temperatures in degC (a) Antoine coefficinets: n-Pentane=1; n-Heptane=2 Ay = 13.8183 Bi cy ‘Ag i= 13.8587 Bos Psaty(T) = ofa - Ti 55 P= 101418 Psaty(T) + Peat) one Since for Raoult's law P is linear in x, at the specified P, x1 must be 7 xy-Psaty (T) apes oo For a given pressure, z1 ranges from the liquid composition at the bubble point to the vapor composition at the dew point. Material balance: xp(i-V)typV V is obviously linear in z vila) os ‘ot 274(b) At fixed T and 21, calculate x1, y1 and P as functions of fraction vapor (V) ( Psat (T) + Psat2(T) v ae 7] Given Three equations relate x1, y1, & P for given V: p= x-Psaty (T) + (1 ~ x)-Psatz(T) yp = Psat; (T) 215 (1-V)x+ Vey F(V) == Find(x,y,p) xi(V) = £1 iV) PCV) = £(V)3 Plot P, xt and yl vs. vapor fraction (V) V:=0,0.1..1.0 100 - 10.4 Each part of this problem is exactly like Problem 10.3, and is worked in exactly the same way. All that is involved is a change of numbers. In fact, the Mathcad solution for Problem 10.3 can be converted into the solution for any part of this problem simply by changing one number, the temperature. 10.7 Benzene: Ay ss 13.8594 By := 2773.78 Cis Ethylbenzene Ay := 14.0045 By := 3279.47 C2 Bi AI icy deel kPa Poatg(T) =e OS kPa10.8 10.9 7 Guess: T (afGiven: x)= 035 yt N6-degC P= 132-kPa Given xy-Psat}(T) + (I —x1)-Psata(T) = P x1-Psaty(T) ® yy-P ©) sa Find?) = Find(P, P i : For parts (b), (e) and (d) use the same structure. Sef the defined variables and change the variables in the Find statement at the end of the solve block. 34.01dexC Ans. -206.95kPa Ans. a ) 111,65-deg_C P= 117.84-kPa (© T= 91.15-deg_C P= 65.66-kPa @) T= 72.12-deg_C P= 35,57-kPa ‘To calculate the relative amounts of liquid and vapor phases, one must know the composition of the feed. To increase the relative amount of benzene in the vapor phase, the temperature and pressure of the process must be lowered. For parts (c) and (d), the process must be operated under vacuum conditions. The temperatures are well within the bounds of typical steam and cooling water temperatures. 13,8594 2773.78 220.07 (1)= benzene Q)=toluene A z= | 14.0098] B= / 3103.01) C:=| 219.79 (3)= ethylbenzene 14,0045, 3279.47 213.20 Psat(i,T) P 2761 Eq. (10.17) 0.441) (b) T= 110-deg_C v y=] 0.333 J P= 100-kPa aaa 0.509) () T= 110-deg C V= 0349 0.312 P= 110-kPa ane 0.573 (@ T* 110-deg_C V = 0.143 y= | 0.283 1 P= 120-kPa — 10.10. As the pressure increases, the fraction of vapor phase formed (V) decreases, the mole fraction of benzene in both phases increases and the the mole fraction of ethylbenzene in both phases decreases, 14.3916 B 2795.82 c (23° 00 14.7258 3271.24) ~~ (241.85 a7 10.11 (a) (1) = acetone (2) = acetonitrile= 115:kPa, _ Psat(i,T) eee. Eq. (10.17) ‘V:=Find(V) -¥ =,0,056 Ans. irk; Eq. (10.16) ic Ans. bee _ 1+V-(ki- 1) yeP x= Ans. Psat(i,T) ae Ans. a (0) x) = 0.286 yt = 0.678 V = 0.545 r= 0.739 (© x1 = 0.182 yi = 0317 Vv = 0.504 r= 0.638 (@) x1 = 0.351 yi = 0.706 v= 0.420 r= 0.594 10.13 Hy = 200-bar Psatg = 0.10-bar Piss L-bar Assume at 1 bar that the vapor is an ideal gas. The vapor-phase fugacities are then equal to the partial presures. Assume the Lewis/Randall rule applies to concentrated species 2 and that Henry's law applies to dilute species 1. Then: 27810.16 yrP = Apxy yorP = x2-Psaty PE ypP+ypP P= Hy-xy +(1~ x1) Psat Solve for x1 and yt: EE P — Psatz Hpxy 1 A — Psat ms 5450201077 WERE Detar oe y= 09, Ans. Pressures in kPa Psaty := 32.27 Psaty := 73.14 A: 067 21 = 0.65 11 (s1.%2) = exp( Anz?) rab 2) = exp(Axr)) (x12) == x1-y(x189)Psatn + x3-73 (01 .x9)-Psaty (a) BUBL P calculation: 2 (x12) Pout DEW P calculation: Psaty + Psat 2 Guess: Given yeP" = xyyj (xr, -x1)-Psaty P= xy-yi(xq,1 —x1)-Psaty (1 —x1)-¥9(x1 1 ~ x1)-Psaty (x = Find(x;,P’) Puew = 43.864 © Ans. \Paew, The pressure range for wo phases is from the dewpoint to the bubblepoint: From 43.864 to 56.745 kPa 279(b) BUBL P ealeulation: XI xeri(ais) x) Pst The fraction vapor, by material balance is: u-X1 yilsi) = x1 (©) See Example 10.3(¢). 892 Ans. v=0379 PR 71 (0, 1)-Psat Paty = O21 = 721 ,0)-Psat Since alpha does not pass through 1.0 for 0 At jen Fo =Find(T) T2°376:433 ns. xp-yyPsaty (1) serene 0.137bar Ans.‘The romaining probloms for this chaptor have boon eclved on MS-EXCEL 2000 We givo the reculting spreadsheets. Problem 10.25 a)BUBLP — T=S0F(S1.41C) P=200 psia ——~P=250psia—«Pa215 psia (14.824 bar) ANSWER. Component oxi Ki yieKitxi KI yisKitxl Ki yiPKined methane 0.100 5600 0560 4800 0400 5150 0515 ‘ehylene 0500-0700 0250 0575 0.288 0650 0.225 ‘ethane 0400 0445 0178 0980 0152 0420 0168 SUM= 1.088 SUM= 0900 SUM= 1.008 close enough bDEWP TOF ESH.ATC) Pat90 pela P=200 psia (19.79 bar) ANSWER. Component yl Ki xiii KI xy mettere 500 $800 0.085 S600 0089 ethylene «0250 0730 0342 0700 0.367 ebane 0250 0460 0543 0445 0562 SUM= 097! SUM=1.008 close enough )BUBLT —P=250 psa (17.24 bar) T=50F T=60F T2587 F (49.44 0) ANSWER Component xi Ki yiekixi Ki Ki yiekixd mettane 0.120 4.900 0582 4600 0552 4700 "0564 etyiene 0400 08800272 ozs 0818 0246 ethane 0.450 0450 0216 0182 o4c5 0108 SUM= 1.076 0962 SUM= 1.004 close enough @)DEWT — +250 psia (17.24 bar) Te40F Ts 50F T= 45 F (27336) ANSWER Component yi Ki xeyiKi Ki xinyKI KI xieyiki menane 0430 6200 0.082 4800 0083 5050 0.085, ayene 0360 0.800 0450 0680 0520 9740 0486 thane 0210 0820 0404 0450 0467 0485 0433 SUM= 0937 SUM= 1.084 SUM= 7.005 close enough 284Protlern 10.25, a)BUBLP — T=600(140F) 200 psa 60 oslo x80 psia (5516 bar) ANSWER Component xi Ki yikrxi KI yleKitei Ki yieKitad ethane 10 2015 0202 6800 0880 4.950 0405 propane 020 0620 0124 2050 0410 1475 0205 Tsobutene «030-0285 GOTT 0780 0234 0.560 0.168 Bopentene 0400071 0028 0205 0.082 0.12 0088 SUM= 0430 SUM= 1405 SUM= 1.006 close enough byDEWP —T=60.C (140 F) P80 psia P80 psia psla (3.585 bay ANSWER Component yi Ki xisylKi KI XIYUKI KI xinyiK ‘thane 048 4950 0097 6.800 0071 8600 0073 propane: 025 1475 a169 2050 0.122 2.000 0126 Isobutane «0150580 0.268 0780 012 0760 0107 isopentare «0.12«012«1.000 «0.208 0585 0195 0615 SUM= 1.534 SUM= 0970 SUM= 1.010 close enough yBUELT 5 bar (217.55 psa) 220F Ta150F 145 F (62.78 C) ANSWER Component xi Ki yiskitxi Ki yieKi'xi Ki yinkital ethane o14 5350 "0749 3.800 0532 3700 0518 propane 073 2500 0325 1525 0108 1475 0.102 ssobutane «02514750368 O78 0.180 O70 0180 ssopentare «048057 ORTH «OFT 01300250120 SUM 1.716 SUM= 1050 SUM= 1.010 close enough ) DEWT 15 bar (217.58 psia) Te150F TeUd5F TH1eB F (64.440) ANSWER Component yi Ki Ming Ki eyK Ki xinyikh ethare 042 3800 0111 3700 0114 amon Ott propane 030 4525 0197 1475 0.203 1.500 0.200 isobutane «O15 0760-0187 0.720 0.208 0.740 0203 ‘sopentane «0.19«O.27OaB1 028 0.820 026 0500 SUM= 0.986 SUM= 1045 SUM= 1.013 close enough 285Problom 10.27, FLASH T=80F (14.81 C) 250 pala (17.24 bar) Fraction condensed 855 120145 ANSWER Component zi vi xiFyimi ethane 050 0875 0.058, ehane 010 0.508, 0.052 propane 020 0787 0275 ‘butane 020 0.529 08:6 41000 SUM= 1.001 Problem 10.28, First calculate equilibrium composition T=95.C (203 F) P=80 psia P65 psia P69 psia (4.83 bar) ANSWER. Component xi KI oyirKinxi KI ikital KE yiFKx butane 025 225 0565 27 067s 26 08s nhewre «O75 O48 0.3375 081 0385 0.49 0.3675 ‘SUM= 0.9000 SUM= 1.0575 SUI = 110005 Clase enough Now calculato liquid fraction from mole balances yi= 0633, ANSWER L= 0.347 Problor 10.29 FLASH P= 200 atm (29.39 psta) T= 200 F (99.3.0) Fraction condensed v= 0.360 [50st ANSWER Component zi Ki yi ai=yuK pentane 0.252.250 0378 0.168 ntwxene 0.45 1.000.450 0.450 mepiane §— 0.300.450 0.172 0.382 SUM= 1.000 SUM= 1.000 286Problem 10.30 FLASH Te40 c (104 F} Fraction condensed v=0.0 Pet10 psia Component zi Ki yt thane 015 8400 0220 propane 035 1900 0482 butane 080 510 0398 SuM= 1.053 Problem 10.31 FLASH TsTOF (21.110) Fraction condensed v= 0.20 te oo P50 psia P40 psi Component zi Kyl xieyiK KI yl ethane 001 7400 0032 0004 9200 0035 propane 0.05 2400 0.084 0038 3000 0.107 outane 050 0925 0470 0508 1150 0.558 butane 0.44 080 0312 0472 aid 0370 SUM= 0907 1023 SUM= 1071 287 xy 0.045, 0248 oot os82 xisyih ‘0.004 0036 0.485, 0487 082 ANSWER P=120 pala (8.274 bar) Ki yl ey 4360 0210 0047 11620 0413 0255 0525 0357 0.800 SUM= 0.999 1,001 ANSWER Pag psia (3.024 bar) Ki yl dey 500 00% 0.008, 2700 0101 0.037 41080 0524 0494 074 0343 0484 ‘SUM= 1.002 1.000Problom 10.32 FLASH Component methane ohare propane eutane ‘Component methane ethane propane rebutane ‘Component methane ohare propane butane T=156(5F) P=300 pela ‘Ve 0.1858 aK oy 030 6600 0,908 040 0820 O08 030 0200 o070 030 ood 07 ‘SUM= 1.078 0.30 o10 030 030 Target: yi-0.8 Leases xinyiki 162 0.103 0382 036 SUM= 0.962 Ls 0.6850 alsyiKi 0.973 088 0.376 0424 suM= 0.960 ‘P=ZTO psia (18.616 bar) Ve 0.2535, Kyi 8200 0.02 0.900 0.082 0.230 0.088 0.0405 0.020 SUM= 1.000 L=07465 ANSWER xeyiKi 429 0103 0373 0.395 SUM = 1.000 288Problem 10.33, First cafculate vapor composition and temperature on top tray BuBL. P=20 psia rear Ts60F 1°69 F (20.86.C) ANSWER Component xi KI yiekitxl KI ying) KI yikitet p-butane 050 1575 0788 1350 0875 1550 O75 pentane «95004500225 0.360 0.180 0440 0220 SUM= £013 SUM= 0855 SUM 0.896 close enough Using calculated vapor composition from top tray, calculate composition out of condenser Flash calculation P=20 psia (1.378 bar) 60 Le 0.s0 T=70F ANSWER Component zi Kyl xisyiK n-butane 078 1575 0843 0402 1350 0890 0.680 pentane «02204500137 0308 0360 0115 0328 SUM= 1.085 0.905 SUM= 1.007 0.983 Problem 10.34 FLASH T40 6 (104F) v= 0.80 Le oso ANSWER P2280 sia 'P=325 psia (7.928 bar) Component 2i yl xing KE yi aeyK KI liegt methane 00 7.900 0768 0.097 11000 o7a6 aor! e400 O772 082 rebutane 050 0235 0217 08a D200 0253 OB7! 0205 O24 914 SUM= 0985 7.021 SUM= 1038 0.943 SUM= 0996 1.006 close enough 289Chapter 11 - Section A - Mathcad Solutions For an ideal gas mole fraction = volume fraction €02 (1): x1 0.7 N2(2): x2 3503 AS = R/S" xirln(s) For a closed, adiabatic, fixed-volume system, AU =0. Also, for an ideal gas, AU = Cv AT. First calculate the equilibrium T and P. ny? i= 4-mol Twa = ((75 +273.15)-K] nar := 2.5-mol Tar = (130+273.15)-K TN2 = 348.15K Tar = 403.15K AN? Mtotal ‘= NN2 + NAr XL 2 — Total Dtotal x1 = 0.615 x2 = 0.385 Cyn2 Cpar=CvartR — Cpn2=CuntR Find T after mixing by energy balance: T2+Ta pie Dna Tar z (guess) Given nz Cen2-(T~ Tr2) = narCvar(Tar~T) T := Find(T) T—273.15-K = 90degC Find P after mixing: Pro + Par 2 (guess) 2803 Given (ny2 + nar)-R-T P P sx Find(P) P= 24.38bar Calculate entropy change by two-step pat! 1) Bring individual stream to mixture T and P. 2) Then mix streams at mixture T and P, ASyo != nN2 (omon( 4) - we P }) ASxq = 11 806-2 2) Pra, iG (ame (ery Sqr = mar] CParln| | — Rel = }\ ASa, = -9.5474 \ Par} . I ASmnix = Mrotat( RS? xi-In(xi)) = 36.006 Smniy = Mt wo yx (3) Sax = 36.0065 Gens AS := ASy2 + ASay + ASprix Ans. mdoty2 molwtng ‘= 28.014-2— molwty = 2.01622 mol mol mdot mot molarflowyy2 me molarflowyg = ———2 molwiy? mola, molarflowsotal := molarflowy2 +molarflowy2 molarflowrotal = 319.409 22 see molarflowy2 molarflown2 yey 0224 yg 0.776 molarflowiotal molacfloweotat Ans. ~R-molarflowjota!: yy ta(y3) 2914 115 Ty = 448,15-K Tz = 3081S-K | Py ss 3-bar For methane: McPH(448.15,308.15, 1.702,9.081-1073, -2.164 107 §,0.0) = 4.82200 ,-2.164:10" 0,0) = 4.79051 McPS(448.15,308.15, 1.702,9.081-10 For ethane: McPH(448.15,308.15, 1.131, 19.225-1075, ~5.561-10" 6,0.0) = 7.59664 eps 448.15,308.15, 1.131, 19.225-10" 3,s.561-10"®,0.0) = 7.53108 MCPH := 0.5-4.82200 + 0.5-7,59664 MCPH = 6.209 MCPS := 0.5+4,7905I + 0.5-7.53108 MCPS = 6.161 AH := R-MCPH-(T2 -T;) aH = 72274. mol (T Pa) AS = R-MCPS-In} — | ~ R-Inj | + R-2-0.5-In(0.5) Th Pry ‘The last term is the entropy change of UNmixing J moh AS = -15.813. Wigeat := AH - Tg-AS Basis: 1 mole entering air. 0.21 y2i= 0.79 Assume ideal gases; then AH = 0 The entropy change of mixing for ideal gases is given by the equation following Eq. (11.28). For UNmixing of a binary mixture it becom 300-K, vie J = Re(y-In(y,) + yeh AS = -4273 8 = R-(yr-ln(y1) +y2-In(y2)) morK He By Eq. (5.27): Wideal := ~To-AS Wideat = 1.282 WS voy Wide! papel By Eq, (5.28): Work := Morn 20a Ane mM <: fi 29211.16 0 1.000 10 0.985 20 0.970 od 40 0.942 0913 bar Z =| 0.885 end := rows(P) 0.869 0.765 is=2..end 0.762 0.824 500 0.910 Fiis a well behaved function; use the trapezoidal rule to integrate Eq. (11.34) numerically. Fi+F; ERP) Indi = ng + Ai 41 = exp(ingi) fis orPi Generalized correlation for fugacity coefficient: For CO2: Ty = 304.2-K 3.83-bar © = 0.224 T = (150 + 273.15)-K = 1391 4 BO = o.0g3 — 2422 BO = -0.166 BI = 0.139 ~ 2172 Bl = 0.096 TS 42 BREE Ty 2 7] Pe | Ga(P) == exp] [-(B0 +0 By fo(P) = OG (PP 283bar bar Calculate values: |” a 8.25] 20 oar 79.555 20 [ome] 37978 | 9} a | 88382 20 o8%6| T1676, 100] 0872! 187 200) O77) 300] [0696 | 400) 0656 500) ‘836 , 8 oe 4a(P i eee 6 i ee ice riaoten Pi ‘bar Agreement looks good up to about 200 bar (Pr=2.7 @ Tr=1.39) 11.17 For S02: 8.84-bar = 0.245 Po P = 300-bar Pr = 3.805 For the given conditions, we see from Fig. 3.15 that the Lee/Kesler correlation is appropriate, Data from Tables E-15 & E.16 and by Eq. (11.64): 20411.18 11.19 090° GRRT := In(6) 6 6 = 0.724 fS27 bar GRRE 0.323. Ans. Isobutylene: Te: 4179-K Pe = 40.00-bar = 0.194 a) At 280 degC and 20 bar: T := (280 +273.15)-K P= 20-bar Tn) = TT) = 13236 PCP) = PP) = 0.5 r(T) 2= ke (7) = 1.323 1! Po rf At these conditions use the generalized virial-coeffieient correlation. PHIB(1.3236,0.5,0.194) = 0.9379 PHIB = 0.9379 f= PHIBP =18.76bar Ans. b) At 280 degC and 100 bar: T := (280 + 273.15)-K. P= 100-bar Te(T) = 1.3236 P,P) = 2.5 At these conditions use the Lee/Kesler correlation, Tables E15 & 1.16 and Eq. (11.64). 60 = 0.7025 $1:5 12335 ¢ = 90919 oe oP £2 73.469bar Ans. The following vectors contain data for Parts (a) and (b): (a)=Cyclopentane; (b) = I-butene _ (0.196 ~ \o.19t S118 45.02 /K Poe bar 420.0, 40.43. 0.273 258 ) om? 322.4 ze(2?) ve ( Ble as x 0277 2393 ) mol 266.9, 383.15 215 5.267 Ts -K P= bar Psat = -bar 393.15, 34 25.83> T in at 0.117 = T; Psat = Psat, = Te (0.9361 Pe 0.6389 Calculate the fugacity coefficient at the vapor pressure by Eq. (11.6: Tr (a) PHIB(0.7486,0.117, 0.196) = 0.9000 (° | PHIB := (b) _ PHIB(0.9361,0.6389,0.191) = 0.7596 0.7596 Eq. (3.63), the Rackett equation: = Th fia ) Tor = Tor = Te {0.635 Eq. (11.41): 97.092 \ om? van = (700? at 91.426 } mol Leh oe £ f be Ans. 20.07 molwt = 18-2 24 mol P = 150-bar cm Veat = 18.342 mol Equation preceding Eq. (11.41), pg. 387: Vear(P —P. seat rom exp Lael Pos) r=1079 rec S079 Ans. L RT eae 11.22 The following vectors contain data for Parts (a) and (b): | molwyt := te mol Table F.2: (a) 9000 kPa & 400 degC; (b) 1000(psia) & 800 degF: 296[ (400+273.15)-K | ny : (800 + 459.67)-rankine 3121.2. el 629152 gm emK AL Bu Sis Btu 1399.64 1.3677 3 Tbprrankine Table F.2: (a) 300 kPa & 400 degC; (b) S0(psia) & 800 deg 1 8.0338-— gorK Bu Heer eee eee Ibn rankine Eq, (A) at the top of page 388 may be recast for this problem as: —————> [ molwe | H2- Hr | (0.0377), rou] Rig ten (2-5) = (o.0sa2) TY @ =2s00n o « aes 11.23 The following vectors contain data for Parts (a), (b), and (c): (a)=n-pentane —_(b) = Isobutylene (© = 1-Butene: 469.7 33.70 0252 Te =| 4179 -K 40.0 |-bar 0.194 420.0 40.43 0.191 0.270 3130), 309.2 Ze =| 0.275 2389/27 tas} 266.3 |-K oan 2393) ™! 2669 200 1.01325 300 |-bar Psat :=] 1.01325 |-bar 150, 1.01325 297> (0.6583 ) — 0.0301 Ta lax 1, = | 0.6372 | p= Pt ad 2s Te i Pe 0.6355 ) 0.0254 Caleutate the fugacity coefficient at the nbp by Eq. (11.65): (a) PHIB(0.6583 0.0301 ,0.252) = 0.9572 0.9572 (b) PHIB(0.6372,0.0253,0.194) = 0.9619 PHIB = | 0.9619 (©) PHIB(0.6355,0.0251, 0.191) = 0.9619 \0.9619 EEE 3857 Eq. (3.63): —_Vsat | vexe! 7) | ‘Vsat-(P — Ps Eq. (1.41): ¢ [pata aten 11.24 (a) Chloroform: T, := 536.4K @ = 0.222 Psat := 22.27-bar Ze = 0.293 Tis 47B.15K T,= 0.882, Tm = 0.623 0257 3 Eq. (3.63): Vsat = Verret tm) Vsat = 94.409 mol Calculate fugacity coefficients by Eqs. (11.65): 0.422 Bt 0139-42 42 Tr BO := 0.083 - 715 BO = -0.433, BI = -0.152 298P(P) re) = 6) = of (90-080) £(P) = af << Psat, 9(P) Pera aten| oy Psat) || uJ he Peat __ [Vane ~ Pat) #(F) =i Ps Pat 9), HP el SE Sa P := O-bar,0.S-bar.. 40-bar (b) Isobutane = 36.48-bar@ 181 Ze 2 0.282 261.4-K 5.28-bar a Th T= 313.1S-K Ty:= — Ty = 0.767 Tm = Tr = 0.641 Te Te 0.2487 3 i Ip) Eq. (8.63): Vsat = Vezg(tm) Vest = 1021052 ‘mo Calculate fugacity coefficients by Eq. (11.65): 0.422 BO cre aerisl BI = 0.139 - 2172 Tr 299BO = ~0.562 > PAP) = 2 = 5 £(P) if S Psat, (P)-P,6(Psat)-Psat ox oP) sat | Wsat-(P — eo] Ps P< Psat,6(P), oo a if 'sat O(P) (Psat) pe Rr O-bar,0.5:bar...10-bar os uP) 06 od aed Bee bar’ bar bar 11.25 Ethylene = species 1; Propylene = species 2 282.3 (50.40 0.087 KK Pe := ‘bar wes 365.6, 46.65 0.140 0.281 131.0) em? Ze= ve =( 22) 22% 0.289, 188.4) mol T = 423.15-K y= 035 n=? HF 300By Eqs, (11.67) through (11.71) (ite i) 1317 1.157, 131 157.966) em? _ 8 aes “(157.966 188.4} mol °° (48.189 46,627 0.087 0.114 282.3 321.261 0.281 0.285 o= Te= K Z= (oid 0.14 321.261 365.6 0.285 0.289 By Eqs. (3.61) and (3.62): BO; j *= 0.083 — on 6 unm () Ty le! 138 nd a _ (0108 ae) 0.189 -0.251 (0.085 0.046 } 892 -99.181 | om? ( 99.181 -159.43) mol ( 0 20.96) a ~\2096 0 } cp 301fhaty := ghaty-P phat pens A ak = phate ab ns, ke OBIS) For an ideal solution, $id = pure species : Po, _ (0595 . i Pr ( Pac = Loa) tide = ox i, BOq,k + Ok Blk, fhatig, = Gide Alternatively, P Pry po idk = exp) (B04, +04 eB) 7 Lica 11.27 Methane = species 1 Ethane = species 2 Propane = species 3 021 0.286 0.43 Ze.=| 0.279 0,36, 0.276, 190.6 98.6 3 305.3 |-K ve =| 145.5 | mol (369.8 200.0 ns3 i 1 3021.958 1.547 1.406 Tr=| 1547 1.222 1.411 1.406 L111 1.009 98.6 120.533 143.378) Ve =] 120.533 145.5 171308 | mol 143.378 171,308 200 (45.964 47.005 43.259) 0.012 0.056 0.082) Pe= | 47.005 48,672 45.253 jbar @=]00s6 1 0126) (43.259 45,253 42.428 ) (0.082 0.126 0.152) ( 190.6 241.226 265.488) (0.286 0.282 0.281) Te= | 241.226 3053 336.006 |K 0.282 0.279 0.278 265488. 336.006 369.8 ) 0.281 0.278 0.276) By Eqs. (3.61) and (3.62): 0.172 (t,) Blj, j = 0.139- By Eq. (11.61): eran 0 30.442 107.809 em =| 30442 0 23.482 | mol 107.809 23.482 0 Ghat. = vos {* vata D Daal 2-85, k- 8) JT hat := ghaty-P 6), j = 2B, )~Bi,i~11.28 For an ideal solution, did = 6 pure species . 0.761 ) 2 + Pros py Pee ozi8| idk 2= ex = (B +0, kBlk,¥)| 0.824 ) bk J “(oan fata, := éidkeP 0.88 Ans. Give: = (2.6.x; -1.8:x2)x1-92 RT () Substitute x)= 1 - x), a =.8-x1 — 1.8)-x)-(1—x1) = -1.8-x) +72 + 0.8x)> RT Apply Eqs. (11.15) & (11.16) for M=GE/RT: (a) S (nm) ‘dx 5 2 Zo -1842-n +24x17 dx) fy, © 1.842814 TA x Ing = 3x1 — 16x)? (b) Apply Bq. (11.95):(©) Divide Gibbs/Duhem eqn. (11.96) by dxt: These two equations sum to zero in agreement with the Gibbs/Duhem equation, (a) When x1 =1, we see from the 2nd eq. of Part (¢) that QED. When xi = 0, we see from the 3rd eq. of Part (c) that QED. (©) DEFINE: g= GE/RT e(x1) = 18x) 4x17 +0.8-x13 In (x1) = 1.8421 + 14x — 16x tnya(x1) = 9? 1.6.x. ‘nye Inypel) x15 0,0.1..1011,32 Xi? 0.02715 0.09329 0.17490 0.32760 0.40244 0.56689 0.63128 0.66233 0.69984 | 0.72792 0.77514 0.79243 0.82954 0.86835 0.93287 0.98233. xi = 0,001.1*) a {3448 10° infit(x1,VE,F)}8} =} 3202,¢10° ec} \ 244.613 Ans. 600 ve} 400 xian Larbatie st") 509 0 02 04 06 O08 1 xxl By definition of the excess properties VE = xpxplatbx; re(xs)?] Bs —t.0-(xy) + 3(e —b)-(xy)? + 24b—aday ta 1 (Vbary)® = (x9)? a+ 2-b-xy + 3-e-(x1)*| (vara) = (x1)?[ b+ 246-9.) +3-e(%)?] (b) To find the maximum, set dVE/dx; = 0 and solve for x). Then use x, to find VE nae Guess: x1 : Given 4o(xl) +3-(—b) (Xl)? +2(b~ a)-xl $a = 0 x1 := Find(x1) X1= 0353" Ans. 307VE mac = x1-(1 = x1)-(a+ bext +0-x1?) (©) vebary(xi) = xt)? [a+ 2-b-xt + 3-6-(x1)? | 2 27 Vebara(xl) = (x1)? a~b+ 2(b~)-xt + 3-6-6419? } x1 = 0,001.1 4000 Years xt) 70 Vebara(x!) é Discussion: a) Partial property for species i goes to zero WITH ZERO SLOPE as x,-> 1. 'b} Interior extrema come in pairs: VEbar min for species 1 oceurs at the same x, as VEbar max for species 2, and both occur at an inflection point on the VE ys. x, plot. ¢) At the point where the VFbar lines eross, the VE plot shows a maximum. 11.33 Propan 1; n-Pentane=2 = (75 +273.15)-K yi 0s 276-466 : islam jedan 466-809 By Eq. (11.57): Be yey Bi, j epi ne om , B = 504.25 22 a 308Use a spline fit of B as a function of T to find derivatives: 331), 558), bil =| -276 |. bits] 466} mol ‘mol mol =235. (399, ( 50) (323.15 us | 15 |+27as K | s4a1s K (00) \s73.15 vsiL := Ispline(t,b11) B1I(T) := interp(vsl!,t,b11,1) BIICT) = 276 moi 3 ys22 := Ispline(t,b22) B22(T) := interp(vs22,t,b22,T) B22(T) = 809 mmol 3 vs12 := Ispline(t,b12) Bi2(T) := interp(vs!2,t,b12,T)B12(T) = -466 mol {anc “Leia aT aT 1.92 3.18) em? abdT = aBat = son Ga 5.92.) mol “arm “par : \at ar 3 Differentiate Eq. (11.57): dBdT := yryydBdT), jdBaT = 3,55 'q. (11.57) DVD vasa ard vi BP By Ba. 37:2 = 14 Z = 0.965 P(B By Eq. (6.54): HRRT == fe ~ sat} HRT = -0.12 HR := HRRT-R-T J By Eq. (6.55): SRR -dBdT SRR = -0.085 SR == SRR-R11.34 Propane =1; n-Pentane=2 T= (954 273.15)-K Pis2bar = yp 05 ais -y : _ {276 -466) om? a2 ~ \-466 -809) mol ari 8),j = 2-Byj- Bi i-Bj,j By Eqs. (11.59) and (11.60): iy es [aed -wer] P 2, hat2(yl) := exp) ——-(Bo > +y! thataCe0 = exp 35 (B2,2+91 81.)} ghati(yt) » yl: 0,0.1..1.0 0.99 0.98 + ghatl (yt) — "0.97 gha2(y1) 0.96 F 09s b oe ocrarei02 oa 06 08 1 yl 31011.36 x= (a) Guess: 0.0426 0.0817 0.1177 0.1510 0.2107 0.2624 0.3472 0.4158 0.5163, 0.6156 0.6810 0.7621 O8181 0.8650. 0.9276 0.9624 xr(I~x1) F(x) :=} x1-(1-x1) x1°-(1-x1) HE; x(t) [asbaxteo(xty?] n= rows(x)) i .0.01..1 “191.7 xls b= 100 c:= 0.01 ree linfit(x1 ,HE,F) Eb bey ° i 100 200 0 02 04 06 08 xppxl anBy definition of the excess properties HE = xpxofarbor te(n)'] a xy (Hoary)? = ()°2 + 2-b-x1 +3061)" } Aee(xi)3 4 3(e~b)(x1)? +2 a)ext ba (Ltbara)® = (x1)*[ a= b+ 24b-e)en1 +3-e(x)*] () To find the minimum, set AHE/dx; = 0 and solve for xj. Then use x, to find HE gig. Guess: x12 0.5 EG) = x1-(1-x1)-(a4 bal tex Given 4-c-(x1)> + 3-(e—b)-(x1)? + 2-(b— a) xl +a = 0. xl = Find(xl) xl 51 Ans. HE min == x1-(1—x1)(a + bxt +x?) Ans. (©) HEbarj(x1) = HEQal) +(1~x1)S-- TEC) ix HEbarg(x1) := HE(s1) - x1 (:. 00) x1 0,001.1 00 —— HEbari(x1) © HEbarp(x1) 500 312Discussion: a) Partial property for species i goes to zero WITH ZERO SLOPE as x,-> 1. b) Interior extrema come in pairs: HEbar min for species 1 occurs at the same x, as HEbar max for species 2, and both oceur at an inflection point on the HE vs. x; plot. ©) At the point where the H¥bar lines cross, the H® plot shows a minimum. 11.37 (a) (1)=Acetone (2) = 1,3-butadiene T= (60+273.15)K P= 170-kPa ua) vif ) cm? 0.267 ©" (20.4) mol ( 0.307 0.2485 0.082 Eq. (11.67) 0.2485 0.19 0.126 0,082 0.126 0.152, ( 5082 464.851 Eq. (11.68) Te =| 464.851 425.2 |K 369.8 0 0.233 0.25 Eq. (11.70) Ze=| 0.25 0.267 0.276 0 ( 209 214.65 Fi Eq. (11.7) ~|[21465 204 | “| mol 200 } (47. 104 45.013 re {esos 42.826 |bar (42480 Note: the calculated pure species Pe values in the matrix above do not agree exactly with the values in Table B,1 due to round-off error in the calculations, Faq. (11.69) Pej, j = 3130.036 0.038 0.656 0.717) Pr=|0.038 0.04 717 0.784} 0.824 0 a Fq.@.61) —BO;,; = 0083-22 (t5;,))'* 0.74636 -0.6361 -0.16178 BO =| 0.6361 0.5405 -0.27382 0.16178 -0.27382 -0,33295 Bq.6.62) Bij = 0139-2 (a) 0.874 -0.558 0.098 ) Bl =|-0.558 -0.34 0.028 0.098 0.028 -0.027 Eq, (11.66) *(B0;, | +: jBli,3) 3 (7210278 “est em’ (665.188 -499.527) mol = om? Eq. (11.57) = yi i eae q. (11.87) B DY DY weve B= 598.524 i jm BP Eq. 3.37) Z:= 1 +} — 4g. RT Ans, 314an Eq. (681) dBldTy;,j = 2 TH i) Differentiating Eq, (11.57) and using Eq, (11.66) en : [i ist j= Eq. (6.80) dB0dTs;,j Eq. (6.54) HR := P. (2 - ana Ans. Eq. (6.85) SR := -P-dBdT Ans. Eq. (6.53) GR:= BP Ans. 3 v= 13694. HR = -450322-— mol mol 7 OR = -125.1-—. SR = ~1.006: mobK mol HR = -175.666-— cm © ‘V & 24255: rT mol aaa eee oR 333.2, molK mol cm J (d) V = 80972-—— HR = -36.48-— mol mol sr = 0.097 oR 1 molK mol om J () V = 56991-— HR © -277.96-— mol mmol SR = ~0.647.—_ 252 molK mol 315Pbs. 11.X1 --- 11.X3 11.XI_ Calculate ¢ and f bar by the Redlich/Kwong equation of state for one of the following, and compare results with values taken from a suitable generalized correlation: (a) Acetylene at 325 K and 15 bar. (b) Argon at 200 K and 100 bar. (©) Benzene at $75 K and 40 bar. (d) Carbon dioxide at 350 K and 35 bar. (e) Ethylene at 300 K and 50 bar. ( n-Hexane at 525 K and 10 bar. (g) Methane at 225 K and 25 bar. (h) Nitrogen at 200 K and 75 bar. 11.X2 Calculate @ and f bar by the Soave/Redlich/Kwong equation of state for the substance and conditions given by one of the parts of Pb. ILLX1, and compare results with values taken from a suitable generalized correlation. 11.X3_ Calculate 6 and f bar by the Peng/Robinson equation of state for the substance and conditions given by one of the parts of Pb. 11.X1, and compare results with values taken from a suitable generalized correlation. ‘Vectors containing T, P, Te, Pe, and @ for Parts (a) through (h): 325 15 308.3 61.39 187 200 100 150.9 48.98 000 575 40 562.2 48.98 210 350 35 304.2 73.83 224 300 50 223) °° | soo 087 525 10 507.6 30.25 301 225 25 190.6 45.99 012 200. 15 126.2. 34.00 | 038 3161.054) 0.244 1.325 2.042 1.023 | .817 > > oes List | te 0.474 Te 1.063 Pe 0.992 1,034 0.331 118 0.544 1.585, 2.206, 11.X1 Redlich/Kwong Equation: Q 0.08664 W = 0.42748 0.02 ) 4.559 0.133 3.234 0.069 4.7 7 0.036 3.998 fia (2 2) CS) B= ost, 680 ae | 504 0.028 | 4.691 0.04 | 3.847 0.121 eas Guess: z:= 1 Given 1+B-qf-——— 3.49) 2(B.,q) == Find(z) z(z+p) Bisai) + ce Ky hn 6.62b) (ay Bia ) ; 4; = exp(Z(Bi,ai) ~ 1 in(Z(8;,qi) - Bi) - gr4)(41.36) Pi 3172(Bi.a) = a5} 722 |. “0668 9987): 9630} 891] O88 0.888) 11.X2 Soave/Redlich/Kwong Equation 2 = 0.08664 = 0.42748 x *) © = (0.4804 1.574-0 - 0.1760 a (0.02 4.49 | 0133 3.202 | 0.069 4737 | 0.036 (v0) 3.19 Pr x Wo i =|] @.s0) -( G51) q= a Ge cag FP 0.028 4.62 0.04 3.827 \o.21 2.304 ) z-B , Given 2=14+B-q-B- (3.49) 2(B,.q) == Find(z) z-(z+B) Z(Bi,ai) + Bi vers nels) oan Z(8i.a) 4; = exp(2(Bi,ai) ~ 1 = In(2(Bi,)) - Bi) - ar) 11.36) fj OrPi 3182(Bi.a aoa L729. on73). Case] 686 683} 6.862) 0.884 11,X3 Peng/Robinson Equation Lay2 Q := 0.07779 Y= 0.45724 —_—> c= (0.37464 + 1,54226-0 ~ 0.269920?) a=[ieeli-1°)F 0.018) 5.383 0.12 3.946 0.062 5.658 a eal sy ga {48 0.073 5.359 0.025 5.527 0.036 | | 4.646 0.108, ] (asa Guess: Given z= 1+B-q-B. (3.49) -2(B.q) 2-8 +e-p)}@+op) Ly 2{8i.a) +06: 242 Z(Bi.4i) +68 ) (6.62b) 319,exp(Z(Bi.ai) - 1 - in(2Z(B;,03) - Bi) ark) (41.36) @ BY GENERALIZED CORRELATIONS Parts (a), (d), (f), and (g) — Virial equation: 325 308.3 15 61.39 187) 350 304.2 35 73.83 224) Te := P= Pe := | $25 507.6 10 30.25 301 225 190.6 25 45.99. ia) = Tek Te Evaluation of 6: eee BO (os cad 2 | (3.61) \ Tr ppo:= 2°75 680) ws [Pr (a) fa 11.6! om (B0 + @-B1)| (41.68) ® (3) 320Parts (b), (©), (€), and (h) —- Lee/Kesler correlation: Interpolate in Tables E.13 - E.16: 1.1842 0.9634 7454 7517, 40= ls 7316 8554, —> os (051°) (11.64): 0.9883 1.2071 321 ‘0.000 0210 ~ | 0.087 0.038 (b) © © @)Chapter 12 - Section A - Mathcad Solutions 12.1 Methanol(1)/Water(2)- VLE data: T= 333.15K 39.223 0.1686 0.5714) (ose 02167 0.6268 | 48.852 03039 0.6943 52.784 0.3681 0.7345 56.652 0.4461 0.7742 = -kPa x ys 60.614 0.5282 0.8085 63.998 0.6044 0.8383 67.924 0.6804 0.8733 70.229 0.7255 0.8922 (72.832 0.1776, 09141 Number of data points: := rows(P) n=10 Calculate x2 and y2: xg = (1-x1) Vapor Pressures from equilibrium data: Psat) := 84.562-kPa Psatg = 19.953-kPa Caleulate EXPERIMENTAL values of activity coefficients and excess Gibbs energy. — — yeP yoP face nese ney ~— R= Shay CENT (x1-n(v1) +2-4n(y2)) 322u,= inf)= h(x) = Gert, = 7] (ee Tom] | [base aos O07 2| [aay 026} [0.85 ci28 0.104 3] [ee 7078] ([Gz7e aT 0.185 a] [286 712 oz 0106 O76] 3] aes v7} fast 31468 ‘a8 6] [x07 cs) 308 0.148 7] [05] qa] [oo oat 0786) 3] [ai vas} [081 03 on7 3] [ras ee aaa O08 vo] [row rai] [oor o348 0.086 os r 7 r 1 oab : 4 (a) Fit GE/RT data to Margules eqn. by linear least squares: GERT; X12, Slope := slope(VX,VY) Intercept := intereept(VX, VY) Slope = -0,208 Intercept = 0.683 Slope + Ai Ans,‘The following equations give CALCULATED values: 1 Gs1 22) = enpl 22[ Ata +2-(Aa1 - Ara} |] y2Gx1 ,x2) := exp] x? Ag) +2-(Ar2- Ari) x2} i O1-j~ 01 Xa, 1101 Xi i i Peale, = Xa 71 (X1, X25) Psatn + X,72(X1, .Xa,) Psat HB aeed eels alia ie ec x 11 (1 .Xa, | Psat Yiecate, i Peale, 5 P-x,y Diagram: Margules eqn. fit to GE/RT data. 90 ;$——_—______—— o| Pj m | soa | Pa atc, 59 nan, *| a 40] Peale 4 30 Wa 20 04 06 08 + X15 Yicate, ot)» Yheale, 500 Px data ° Py data P-x caleulated — Pycaleulated 324Peale, xa¥l (a1, .82)) Psatr +x2,72(x1,.82,) x1 71(31,0%2,) Psat Yicale; \ Peas, RMS deviation in P: RMS = 0.399kPa (b) Fit GE/RT data to van Laar eqn. by linear least squares: X1 99, VXi5= x1, VYj: GERT; Slope := slope(VX,VY) Intercept := intereept(VX, VY) Slope = 0.641 Intercept = 1.418 1 i ay2 = ——— a= Intereept (Slope + Intercept) ap = 0-705. ag i | apy x2 21 ne YG x2) = exp] apy 1 EY a2" 0485 Ans. a A(X1,x2) ~ af + 101 Xi, = 01, ~ 00999 (To avoid singutarities) X, -x 1 325Peale, = Xy 41 (Xi .Xo,} Psat 4X2, 2(X1,X2,} Psata Peale, = x1, 71 (81, .%2,}Psaty +29,-72(1,.X2,) Psata Xt V(X Pea X2,} Psat x11 (x1, %2,) Psaty Yleale, = Yicale, = id Peale i P-xy Diagram: van Laar eqn. fit to GE/RT data. 0 ~ 80 qe) iPa coo Pi 60 kPa ic) Peale; a 4g Peale; de Wa 30 a al 20 109 02 a4 06 08 L XTX,» Yea; coc Px data ° Py data —— P-x calculated —— P-y calculated RMS deviation in P: RMS = 0.454kPa 326(©) Fit GE/RT data to Wilson eqn. by non-linear least squares. Minimize the sum of the squared errors using the Mathcad Minimize funetion. Guesses: Agu = 1.0 SSE(A 49,431) != ze + (ron +412) : I i Seapine, +1821 ig 11(Xi,0%2,) Psat + x9, 72x12, } Psatz Veale, ca ale, Peale; 1 327P-x,y diagram: Wilson eqn. fit to GE/RT data, 90, 0 Pi im 7 2 6 is Peale; a i 40 a ao we 20 ue 0 coor 0.6 08 ¥1 XA» Yieate, 000 P.x data = - data x calculated — Py calculated RMS deviation in P: RMS = 0.48kPa (4) BARKER'S METHOD by non-linear least squares. Margules equation. Guesses for parameters: answers to Part (2). yi (xt x2, Aq2, Aan) i= exp| (2) Ata + 2-(Agt - Aa): xt] ‘yo (xl x2,A12,Aan) == exp] (xt)? Aor +2-(At2- Aoi) 2] 328mize the sum of the squared errors using the Mathcad Minimize function. Guesses: An $ Agi = 10 \ 2 1,74 (1,092, -412,Aat)} Psats .. | 1,992, >A12,A21)} Psat X171(%1,.Xa,.A12,A21) Psat + X2,-12(%1 Xo, Ar2,Aat) Psata gL wate ate Xx 7a( XX Az, Aa) Psaty Peale, x17 1(81 982, A12,A21) Psat. +2,72(m1,, 2 »Ai2,Aai} Psaty (19%, Ai2,Aat} Psaty Yicale, Peale RMS deviation in P: RMS : RMS = 0.167kPa 329P-xy diagram, Margules eqn. by Barker's method 0 — 80 Bi ‘KPa 70. aco eeiaried ira Sc30, Peale; a 40 Pealey 39 wa 20 0 q CSR a 1 sapedIyeXty- Ylcaey aco P-x data Ed °° P-y data P-x calculated — P-y calculated Residuals in P and yt PP, os . : KPa o Xe ¥1,-Yteale;} 100 tte i. br : AEE v2 0406 08 x1 Xx % Pressure residuals yl residuals 330(e) BARKER'S METHOD by non-linear least squares. van Laar equation. Guesses for parameters: answers to Part (b)- 1.101 X1, = OL) ~ 00999 Xa, f / 2 ayaxl = exp) ay2:] 1+ mp x2 ey? = exp) agy-| 1+ alaxl ‘Minimize the sum of the squared errors using the Mathcad ) vist .x2,a;2,a21) ‘7a(x1_.x2,a12.a21) mize function. Guess "| ay2 = 0.5 ayy = 1.0 1) ELF (earn) ee : ] i L +0,°72(%1 982, 412-821) Psat Minimize(SSE..a12,a21) ( SSE(a12 fa) (arr) Pea = X1y11 (Xo Xay 12a} Paty +Xo.-yo(X1.,.X2,.012,821)-Psatz 7X1 -Xoy. 012,21) X17a(X1,X2,,a12, 421) Psat Beg ed eee ee era aE leat, fa ale, Pate, = X1;71(%1).%2,,412,821) Psat +2, 2(1,82,,012,821} Psata x4, 71( 1,582, 08120801) Psat Ycale, Peale, 331RMS deviation in P: RMS = 0.286kPa P-xy diagram, van Laar Equation by Barker's Method 90 80 10 aaa 60 50 Peale; 40 20 15 02 oa oe 08 1 Na 9191) Vooal 900 P-x data a © Pry data — P-x calculated — P-y calculated 332Residuals in P and y1. Pi-Peate; os ke (¥1,-¥teate;} 100 ‘i oo 02 04 06 08 4 200% Pressure residuals © yl residuals (®) BARKER'S METHOD by non-linear least squares. mn equation. Guesses for parameters: answers to Part (c). j= .1ot Xi, = Ol j-.01 J ya (x1 .x2.A 12,821) == exp -In(xt +x2-A 42) rin sts) | ! y2(xt.x2.A12-Aa1) #= exp) -In(x2 + x1-A1) (_ -An Aa } + fei) ee J#X2AqQ xX2#X1-AQ Minimize the sum of the squared errors using the Mathcad Minimize function. Guesses: AjQ = 0.5 Ag, = 1.0 3331 (1.8, r20Aau)Psaty i 2,2 Aai) Psaty i + x27 S9E(A42,A21) “rte Ca ee 4198) (N27) (‘*) := Minimize(SSE,Ay2,A24) ( e Agi) Aa. Peale, = X17a{X1,oXa,Ay29Azi) Psat Xa. X1,,.X2.,Ay2,A21)-Psata, X171(%1,-%2, i242) Psat Yieale, *= ea Peale, Peale, = 51,71 (81,982, -125.Na1} Psat +%, *72(¥1,9%, 412-429) Psat x7 (%4 92, A 2,21) Psat ¥ieale; RMS deviation in P: be RMS = 0.305kPa 334P-xy diagram, Wilson Equation by Barker's Method iPa ooo Peale; kPa Peale; 90 80 20 10 0 Residuals in P and yl. Pi-Peal, Pa wx (X1,-Meale;) 100 02 oa 06 0 tpt pX1y Viole 280 Px data © Pry data P-x calculated — Py calculated q = eo os x 4 x s : “05 * so 02 oa 06 x, **% Pressure residuals © yi residuals 0812.3. Acetone(1)/Methanol(2)-- VLE data: T := 328.15-K 72.278 0.0287 (0.0647 75.279 0.0570 0.1295 | 77.524 0.0858 0.1848 | 78.951 0.1046 0.2190 | 82.528 0.1452 0.2694 | 86.762 0.2173 0.3633 | 90.088 0.2787 ose | 93:206 0.3579 04719 | 95.017 0.4050 0.5133 96,365 0.4480 0.5512 Ps -kPa x yess 97.646 0.5052 0.5844 98.462 0.5432 0.6174 99.811 0.6332 0.6772 99.950 0.6605 0.6926 100.278 0.6945 0.7124 100.467 0.7327 0.7383 100.999: 0.7752 0.7729 101.059 0.7922 0.7876 99.877 0.9080 0.8959 99.799 0.9448 0.9336 Number of data points: n == rows(P) Calculate x2 and y2: oy Vapor Pressures from equilibrium data: Psat; = 96.885-kPa Psaty = 68.728-kPa 336Calculate EXPERIMENTAL values of activity coefficients and excess Gibbs energy. —? — yeP —.—_ Ui eee GERT := (xy-in(y)) + x2"In(2}) i 1 72, Infra.) = lafr2,) GERT, 7] [ew Tom Om 0.75] O27] 2] [i765 oH 0588 oot ‘04s DB) pz 7005] [0544] 5a 105 082 al [766 1002] [ose 7975107 0.068 5 158 To28) [048 0.028) 0.089 8) aar 1027 0.404 0.027 0-108 7] F386 087 0.384 0.055) O78 @| [izes 1.103} 025 0.086 0782 3} [aaa 773] [ote 0725) 0161 To} [az va] fozae 073 0.163 Ti] 66 iiss} [0753 oa77 0.105 v2) ats5| 72 o.taa] 07182 O76 73] [toe 1278 0087 O88 O64 7a] 83] 1317 ore 0275 rd 7] prose 1378 0.06 oa] = [ors 76} [hos Tas Doe [oss 0-128] 7] [ioe 7a] [0059 0385 oni9| v3] [057 rar] [0056 ‘o407 ons 193] [ao yeaa] [o0i7| cd ‘oe 30] [rove sar] — foots] 0558 048 33706. ' T Sof 4) o4 tnfy2i) . GERT 95 VXi'= Slope := slope(VX, VY) intercept(VX , VY) Slope = 0.018 Intercept = 0.708, Aa := Intercept Agy = Slope + Ara 0 Aus. AS Alas The following equations give CALCULATED values: 4G 5x2) = expl 27 Arn +2¢(421 - Arg)xt | ania) j= 1.101 X1,:=01j-.01 Xo i= 1-Xt i 22Cxt ,x2) = exp] x17 Agy +2-(Ar2 i Peale, = X71 (Xa, .Na,) Paty +X, 12(X1,X2,} Psat X1y71(%,.X2)) Psaty Yicale, j Peale, 338P-xy Diagram: Margules eqn. fit to GE/RT data. 10s 100 95 90 85 ° 02 04 06 08 14.91 -%1j» Yreale; B00 P.x data © Py data P-x calculated — Pry calculated RMS = 0.851 kPa 339(b) Fit GE/RT data to van Laar eqn. by linear least squares: xi, VX} = x1 VY = i GERT; Slope := slope(VX, VY) Intercept := intercept(VX, VY) Slope = 0.015 Intercept = 1.442 1 L ans a= Intercept (Slope + Intercept) 21 = 0.686 Ans. r . ' anrx2) y2(x1 x2) := exp) apy 1+ L airxl) j= 1.101 X41, = .O1-j — 00999 (To avoid singularities) X: -X, 35 4 = Xt; 1 (X1,.X2,)-Psaty +X, ¥2(X1,.X2)} Psat x1, 71(x1,.%2)} Paty +2, 72(x1,%2,) Psat irl x Yieale, = 340P-x.y Diagram: van Laar eqn. fit to GE/RT data. 105 100 Pi ime % cao a) kPa Beate Peale; KPa 9 Peale, fe 10 y 02 Y 06 08 1 saa P.x data © Pry data — P-xcalculated — Py calculated RMS deviation in P: RMS = 0.701kPa (© Fit GE/RT data to imize the sum of the squared errors using the Mathcad Minimize function. ‘on eqn. by non-linear least squares. Guesses: Aqg = 05 Agi := 10 SSE(A12-Az1) = °[GERT + (x1,-Infxr, + 92,412) fi +X; Inf +21) } 3MAr = Minimize(SSE ,A 2,421) Aa egjo(—M2 Aan “Usd #x2-Aqg x2 +x1-Agy 1 ee (14x20 Ag exp] —x1.| ——>__ eae xL+x2A1 dates (x2 +x1-Agi) 101 X= 01 j-01 i 1-71 (Xr Xa} Psats + Xo,-¥2(X1, Xo} Psat 111 (1,099,) Psat + x9, P(s1,.92,} Psata Xt A(X sX, ees Peale,P-xy diagram: Wilson eqn. fit to GE/RT data, 105 100 Bi ipa 95 eso fi 90 iP o 85 Peale, Wa a0 Peal; 95 Wa 2 6s 0 02 04 06 08 x17 %y» Yee, 909 Px data © Pry data — Px calculated — Py caleuiated RMS deviation in P: RMS := RMS = 0.361 kPa (a) BARKER'S METHOD by nor Margules equation. ear least squares. Guesses for parameters: answers to Part (a). exp] (02° [A12+2(Aat~Ana}xt | tral} x2. Aiz,Aa1) = exp], (1)? Aor +2-(At2 — Aor 2] | vast x2,A12,A21) # 343Minimize the sum of the squared errors using the Mathead Minimize funetion, Guesses: A= 0.5 Aa = 1.0 S8E(Ar2,A21) = Do]Pi~ (x4p7a(%1,.¥2,,A12, Az) Posty T (exepra(syn9,-ArzsAai) Psat) (Ai2\ = Minimize(SSE,A12,A21) Ans, (Aor Peale, Xj 71(%a, Xo, -Ar2,Azs) Psat + X2,-72(X1, Xo, A12,Aar) Psate dilate X1y71(X1,X2,,A12, Aas) Psat y uss ieeeltteeee teal, Peale, Pate, = ¥1;71(81, 2, ,A12,Az1) Paty + 82,°72(1,.%2,,A12,Azi) Psata 1,71 (41,082, A12,A21} Psat Neale, # as RMS deviation in P: (Pi-Peat,)? RMS := od RMS = 0.365kP: [= 65kPa iP-x-y diagram, Margules eqn. by Barker's method Pi kPa By Pe Peale; kPa Peate, Pa 105 100 95 90 85 80 0 a 9 02 oa 06 08 1 X, YI,» X1, 5 ¥leale, coq pxdta | | Ft ° Py daa — P-xcaleulated calculated x 200% Pressure residuals © yl residuals 345(e) BARKER'S METHOD by non-linear least squares, van Laar equation, Guesses for parameters: answers to Part (b). 101 XI 01-j — .00999 (xt x2 ) wae (1228) (xt ,x2 012,021) = exp, 212 " i ara) r -2 agrx2)? ya(x1x2,4)2,021) ova (1+ a ) | ayzxl Minimize the sum of the squared errors using the Mathcad Minimize function. Guesses: aya i= 05 ay = 10 SSE(a12,221) ay ae Psat. } r i #¥0,-7(%1,.%9, 28125821) Paty sag Ans. 0.672) Pt ) := Minimize(SSE.,a)2,a21) (2) 2 = Xj -71(X1,,X2,.a12,a91} Psat ale 1X2, ri) Psat +Xo,-y2(X1,.X2, .a12, 421) Psat 2,°¥2(X1, °X2, -a12,a21)-Psaty X4-7a(X4, Xz. 012,021} Psat 171%, .%2,-a12,421) 1 Peale; up7 (1, 9%2,412-821) Psat) $x, ¥2(%1, 82,412,221) Psat x4,71(,0%2, 412,821 Paty Yieale, == 7 Peale,RMS deviation in P: P-xy diagram, van Laar Equation by Barker's Method 105 100 90 85 80 15 70| cd 0 0.2 04 0.6 08 sep X1j-Yreae, 000 P-x data © P-y data — P-x calculated — P-y calculated 347Residuals in P and y1. 1s xxx (v1,-¥1eaK6;} 1000 of 06 (OS 1 x, *%* Pressure residuals © yl residuals () BARKER'S METHOD by non-linear least squares. Wilson equation. Guesses for parameters: answers to Part (c). 101 X1, = 01 j-.01 j ya(xt.x2,Ag2sAar) = exp) -In(xt + 22-42) (An An) +x2/ XI HXZAqg x2#xL-AQ,) yo(x1 ,x2,A42,A21) = exp| —In(x2 + x1-A21) 1 (_-An Migee al Xl4x2-AjQ 24KI-AQ) | ‘Minimize the sum of the squared errors using the Mathcad Minimize function. Guesses: Ay = 05 Ag = 10 348SSE(Aj2.A21) aoe Pi— (171 (¥1,.%9,.A.20Aau) Psat = +X, 2( 81, %2,.12-Aa1) Psat (Ar eee = Minimize(SSE,A.12,A2)) reale, = Xi 71(X1,.X2,.Ay2,Agt)-Psaty .. Peale, ayn 1X2 Ara 21) Psat) +X2.-72{X1,.X2,4A12,Agq)-Psaty 2,72 1).%2, Ar 2} 'satz Xx (%, %2AraeAay) Psat Yicale, = a Peale, Peate, = x1,-11{1,83,-A12.A2i) Psat. + rar(m, oe 2421} Psat x] a(x 190, -Ar2, Aoi) Psat Yesle, = ——— Pes RMS deviation in P: ee RMS = 0.35kPa 349 JP-x,y diagram, Wilson Equation by Barker's Method los - 100 2 Pi ia 9s| ooo zal 0) Pa Peale, 85 ia 80 Reales 95 ia — 7» — oO 02 04 06 08 1 MpypX oY) 101% Yieale, 900 P-x data © Py data — Px calculated — Py calculated Residuals in P and y1. {Piya} 100 xy xxx Pressure residuals © yl residuals 35012.6 Methyl t-butyl ether(1)/Dichloromethane-VLE data: T= 308.15-K ‘83.402 0.0330 ota 82.202 0.0579 0.0254 80.481 0.0924 é0416 76.19 0.1665 i804 72.442 0.2482 anise 68.005 0.3322 0:1975 65.096 | swe | Oat? 022457 59.651 0.5036 oY) 63686 56.833, 0.5749 04564 53.689 0.6736 aseed 51.620 0.7676 07176. 50.455 0.8476 09038 49.926 0.9093 5002 49.720 0.9529 0.9502 —— (x ya = (1-y:) Psaty 2 49.624-KPa Psatg := 85.265+kPa Calculate EXPERIMENTAL values of activity coefficients and excess Gibbs energy. — yoP xpPsaty 7? Gp.Psatg —> GERT GERTx1x2 n= 14 XP-X2 351(a) Fit GE/RT data to Margules eqn. by nonlinear least squares. Minimize sum of the squared errors using the Mathead Mini Guesses: Aqz = -0.3 Cc ize function. SSE(A12,A21,C) = [oerti (Aaixa, # Aang, ~ C-x1,99, a Ar) Aa, | = Minimize(SSE,A12,Az1,C) te Ans, (b) Plot data and fit GeRT1x2(x1 ,x2) (Agpxd + Aizx2 - Cx1-x2) GeRT (xt ,x2) := GeRTxIx2 (x1 ,x2)-x1-x2 tpl (x x2) == 32? Ay +2(Azt Arz Cal +3-Ca"| Iny2(x1 x2) xi? [aa +2-(Ai2~ Ag - C)x2+3-C 22°] 108 Xi i= 01 j-.01 Xo I= Xi i GERTX1x2; e GeRTx132( Xr, X: Ppa) -0 i) ty (% 9) ing) sa) os 8a OSs nipX ape eXtp XI AI XI, 362(c) Plot Pxy diagram with fit and data y1@c1 ,x2) := exp(Iny1 (x1 ,x2)) y2(xl x2) := exp(Iny2(x1 ,x2)) Xpyl(X1,. Psaty + X2-¥: »X2, 111 (%1,oX2,} Psat + X2,-72(X1 0X: Peas ) Psat X171(X1,.Xo, Psat Peale ‘ale, P-xy Diagram from Margules Equation fit to GE/RT data, 40 ° 02 oF 06 08 XI ¥1jo%1 Veale; 900 P-x data © Pry data P-x calculated — Py caleulated 3GERT; : GeRT(X1,0%2, GERT; n In] — 12, 3530.004 T ° Po6 0 8GERT; 0 fee ooo Blny1y . a X= 9.005 1 a: 05 1 “005 Xi, Calculate mean absolute deviation of residuals + 7 _——» mean [SGERT| ) = 9391 x 10 smean([sinyiy2}) = 0.021 (e) Barker's Method by non-linear least squares: Margules Equation yi (xt x2.A12,A21C) = exp] (x2)°-[A12+2-(Aai - Ai2- C)-x1 L+3-C-x12 yo(xt x2,412,A21,C) -) [Ao1 +2-(A12 Any C)-x2 ‘| |ys0007 Minimize sum of the squared errors using the Mathead Minimize function. Guesses: Ay = 03 Agi = C02 } 4 88E(A12,Aa1,0) = S/Pi~(aa,71(%1,.¥2,,A12,A01 ,C}Poaty ...P Pa 12(m1,.%2, Aiz Agi ,C)-Psaty AQ Agr | := Minimize(SSE,A2,A21,C) c Ans. 354Plot P-x,y diagram for Margules Equation with parameters from Barker's Method. Pea X1p71(X1 Xo, »Aiz Aan C} Psat Hacetipaeed +X2 2(X1;-%2;-A12,421 0) Psatz x a1i(X Xoj-Ar2,A2t .C} Psat Yiealey = Pas i 90 80 60 so 49 0 02 04 06 Os 1 X14 X1, Yale 19¥1j X15 ¥reale; 900 P-x data ° Py data —— Px calculated xy calculated Peale, = X1;°71(%1,9%2,-A12+A21 .C) Psat + N2,-¥2(X1, 9X2, -Ai2,Aa1.C} Psat x1,°79(%1,.%2, -A12,A21,C) Psat Yieale E Peatc, 355,Plot of P and y1 residuals. Peale; kPa XxX (rvteay en 05 1 x XXX Pressure residuals © yl residuals RMS deviations in P: RMS = 0.068kPa 36612.8 (a) Data: (0.0523 1.202 1.002 0.1299 1307 1.004 0.2233 1295 1.006 0.2764 1.228 1.024 0.3482 1.234 1.022. O.4187 1.180 1,049 x1 =| 0.5001 ‘L329 y=] 1.092 0.5637 1.120 1.102 0.6469 1.076 1.170 0.7832 1.032 1.298 0.8576 1.016 1.393 0.9388 1.001 1,600 0.9813, 1.003, 1.404, J sz rowel) im lan GERT; = x1,In(y;,) +32;n(72,) (>) Fit GE/RT data to Margules eqn. by linear least-squares procedure: GERT; Slope = slope(X.Y) Intercept := intercept(X, Y) Slope = 0.247 Intercept = 0.286 Ajg = Intercept Agi := Slope + Ai A Ag) =0534° Ans, YIG&1.x2) s= exp] x27 Aa +2-(Ag) —Ardac || P2681 x2) += exp x17 Aas +2-(Ar2— Ar) ] | GeRT (XT x2) = x1 -In(y1 (x1, x2)) + x2-In (y2(x , 2) 357Plot of data and correlation: GERT; aac GeRT(x1,.%2)) 0.4 mea) infr(er, 22) oa 0 x, {c) Calculate and plot residuals for consistency test: 8GERT; = GeRT(x1,.%2,) - GERT} Biny 172 = In| = In| (PQ) Le, 3688GERT)= — Sly 1y2i = on EES aes |-2.264-10 3] |-9.153-10 “5 Sos a sao 30 2.87410 -3) -0.019) sted [22210 3| 5.93410 > aie wom] rh |-1.553-10 -3| 9.5910 3! |-8.742-10 + 9.139-10 3} ° 6.96210 5) l 0.011 '9.025:10 5 9.028 423640 + 188 Calculate mean absolute deviation of residuals: rmean(|SGERTI) = 1.615« 107? mean [Biny 12 ) = 003 Based on the graph and mean absolute deviations, the data show a high degree of consistency 12.9 Acetonitrile(1)/Benzene(2)- VLE data T= 318.15-K 31.957 0.0455 0.1056 33.553 0.0940 0.1818 35.285 0.1829 0.2783 36.457 0.2909 0.3607 36.996 0.3980 04274 37.068 0.5069 0.4885 Ps kPa x= we 36.978 0.5458 0.5098 36.778 0.5946 0.5375 35.792 0.7206 0.6157 34.372, 0.8145 0.6913 32.331 0.8972 0.7869 30.038 0.9973 0.8916 359— ty) Paty = 27.778-KPa Psaty = 29.819-kPa Calculate EXPERIMENTAL values of acti Gibbs energy. a= (om coefficients and excess > —>» yee yo? —_——- ae GERT = (xy-n(y}) + x2-In(72 " yppeat, 1? Sp Paty (xrin(ry) +92trGi9)) — GeRTaix2:= SERT se rows) an = 12 xVx2 (a) Fit GEART data to Margules eqn. by nonlinear least squares. Minimize sum of the squared errors using the Mathead Minimize function. Guesses: Ag=-03 Ane -05 C02 SSE(A12,A21.C) = Si [sern (Aat x1, F A12x2, — Cor x (1.028 1.155 Ans. cP Nosy Minimize(SSE ,Ay2,A21,C) (b) Plot data and fit GeRTH1x2(X1 ,x2) 25 (Azi-xl + Arzx2 - C-x1-x2) GeRT(x! ,x2) = GeRTX1x2(x1,x2)-xT-x2 byl (xt x2) = x2? [Arg +2(Aaq —Ar2—C) xt $3-C-x1| Iny2(x1 ,x2) = x1? [ani +2-(Ai2— Ag -C}x2+3-Cn2?| js t.lol Xp, = Ol j-.01 Xo, = 1-X, 1, i 2, 4, 360GERTx1x2) GeKtrsha(%.%2) ta(ru) ‘wrt(Xi,.X2) Infra) n(x, %2,) 0 02 04 06 O08 1 X1oX1) 84X11 XI 1X, XI oI XI (©) Plot Pxy diagram with fit and data ‘YAGI ,x2) := exp(Iny1 (xt .x2)) 72(x1 ,x2) 2= exp (Iny2(x1 .x2)) ie = Xp -71 (Xp, ,.Xz_}-Psaty + X2,-y2(X1,,X2_}-Ps ale, = Xayrtl(X1, Xo,}-Psats + Xoy-y2(Xa, Xo} Psats Xi (x Yieale, = ‘i 361P-x,y Diagram from Margules Equation fit to GE/RT data, 38 36 0 02 oF 06 o8 1 x1pe¥te Xt, Yeale 1M Xt; eae; P-x calculated — Pry calculated (d) Consistency Test: SGERT; == GeRT(x1,.¥2,) - GERT} (ri ha, 2) y fy.) Sly 1y2j = a Eee No iG ra (1,2) J ont ; ~ | - : of x we x SGERT; of. Pee eco any ty2; o Per Pea ae oO 05 1 0.05Calculate mean absolute deviation of residuals es smean( |scert!) = 6.237104 mmean|[Siny1y2}) = 0.025 (©) Barker's Method by non-linear least squares: Margules Equation ya (xl x2,A12,A21,C) = exp) (x2)*[ Ain +2-(Aai — Ai2—C)-x1 [43-C-x1? | als 32.A12.A21.€) a. +2(Ai2~ Ai ~ O)2 | +3-C-x2? Minimize sum of the squared errors using the Mathead M Guesses: Aigi= 0.3 Agi = -0.5 Cs SSE(Az.A21.C) | 2 x71 (,o%9,-A12,A21 C} Psaty .. YP 2(xi 82,-A12,Aat C) Psat An Agi b= Ans. Cc Plot P-x,y diagram for Margules Equation with parameters from Barker's Method, Peate; = Xa,7i(X1 Xa, .A12,Aa1 ,C)-Psat «. Hacer one +X2y-72(X1,.X2,,A12,Aa1 C)-Psata X171(%1,-X2, A122) .C}Psaty esadewvaedeal Yieale; Peale ey 36338 OO 36 34 32 30 28 6G 02 oa 06 08 1 Xp YI, 0X1, ¥teate p00 Px data 2 H 2 Pry data P-x calculated — Py caleulated Peate, = x1, 71[¥1,9%2, A12,A21 ,C} Psaty +9,-72(%1,0%2,-A12,A21,C}-Psata Nip 11 (81,999, -A12,A01,C)-Psaty Yieale, oa 364Plot of P and yl residuals. 06 04 peace Pi-Peate i 02 . ~2} , eo 05 1 x, XXX Pressure residuals © yl residuals RMS deviations in P: RMS = 0.04kPa 36512.12 It is impractical to provide solutions for all of the systems listed in the table on Page 460; we present as an example only the solution for the system 1-propanol(1)/water(2). Solutions for the other systems ean be obtained by rerunning the following Mathcad program with the appropriate parameter values substituted for those given. The file WILSON.med reproduces the table of Wilson parameters on Page 460 and includes the necessary Antoine coefficients. Antoine coefficients: 1-Propanol: Al := 16.0692 BI Cl := 204.00-K a ‘Water: AD := 16.2620 Psaty (T) s= ex al 7 Psata(T) = B2 xp] A2 - ————=___ | kPa T — 273.15:K) + C2 Parameters for the Wilson equation: 3 75.14 vi mol al = 775.48-2a mol v2 ~al2 { -a2 AIQ(T) Boo 22) A21(T) wer 21) vi RT RT x1+x2-Al2(T) x2 +x1-A21(T) (x1 +32-A12(1)) | ( AI2(T) AZT) | exp|-x1{ AZO) __ A) xL+x2-A12(1) x2 #x1-A2I(1), (x2 + x1-A21(1)) evfo[ A12(T) AQT) I yl (xl ,x2,T) = a 201, x2,1) = 366P-xy diagram at Tos (60427315) K Guess: P := 70-kPa Given P= xb-yl(xl 1 = x1,1)-Psat (1) + (1 = x1)-y2(x1, 1 + x1, T)-Psato(T) Peq(sx1) := Find(P) xI-y1 (1,1 —x1,7)-Psati(T) yeq(x!) x:= 0,0.05.. 1.0 Peq(xi) Peq(x) _ yes) = ke a 0 9.024 0.5; o3i7 oa 0.368 [ors 0384 oz 0398 035 oa08 [es oata [035] [042s] oa 032 [045] aa | os] 084 O58 O68 08) O84 [bas] 0503} o7 om? [7s] O587 03 0598 O85 OBA 0a] O71 0.85 0825; t 704 06 08 1 x. yea) 12.13. It is impractical to provide solutions for all of the systems Yisted ta the table on Page 460; we present as an example only the solution for the system I-propanol({)water(2). Solutions for the other systems can be obtained by rerunning the following Mathcad program with the appropriate parameter values substituted for those given. The file WILSON.med reproduces the table of Wilson parameters on Page 460 and includes the necessary Antoine coeffi Antoine coefficients: L-Propanok = Al := 6.0692 BL == 3448.66K Cl 104,09.K Water: 16.2620 B2 == 3799.89-K C2. = 226.35-K Bi |aPa Psat; (T) ——<$—$—_—— ae (T-273.15-K) + Cl B2 i) Ag eceeceeee DCE (T= 273.15-K) +C2 | . 368 Psata(T)Parameters for the Wilson equation: 3 3 75.14. v2 = 18.07: ‘mol mmol vie ad = 775.48 aa = 1351.90.28 mol mol oxf o( A201) an) YI ate xi+ x2 +xPA21(T) }] at (x1 #x2-A12(T)) wfn{ tm so) (xl +x2-A12(1) xd Deararicn)} (x2 + x1-A21(T)) y2G1,,x2,T) = ‘T-xy diagram at P == 101.33-kPa Guess: T= (90 +273.15)K Given p= xteyl(x1,1 —x1,7)-Psaty(T) . + (1 = x1)-y2¢x1,1— x1, 1)-Psatg(T) Teq(xl) := Find(T) xl-y1(x1 1 — x1, Teq(x1))-Psaty (Teq(x1)) = yeq@l) 7 x= 0,0.05..1.0 369Teg) x= yeq(x) = K o a ag oa 0305 364133 on 0368 Bear O15 0383| 361805) 02 0.308 189) 025 0.408 31251 03 ‘oai9| 364.067 035 08) 35095 oa aaa 360876 Zs oasa se08aa os 0.463] 360,068 055 0.486] 350549 oe ‘508 wat 065 0528 e371 o7 0.555 BeL7e7 ‘ors 089 362.208 08 0633 365.073 085 0687 364.173 a9] o768 a 095 0859) 67 RB 7 7 arom, ‘T.xy Diagram at P 315, Teal). 370 x, yogi) 37012.14 It is impractical to provide solutions for all of the systems Tisted in the table on Page 460; we present as an example only the solution for the system -propanol(1)/water(2). Solutions for the other systems can be obtained by rerunning the following Mathcad program with the appropriate parameter values substituted for those given. The file NRTL.med reproduces the table of NRTL parameters on Page 460 and includes the necessary Antoine coefficients. Antoine coefficients: 1-Propanol: Al : 16.0692 BI = 3448.66-K CI = 204.09-K. Water: = A2:= 16.2620 B2 := 3799,89-K 226.35+K Psaty(T) Psatp(T) := exp] A2- 82 ___ | xpa (P= 273.15K) +2 Parameters for the NRTL equation: biz z= 500.4024 ba i= 1636.57. 5081 mol mol +12(T) bar RT G12(T) := exp(-a-412(1)) G21(T) = exp(-c-121(7)) 2 an A(t ,x2,T) == exp} x2" £21(7)| ————___|_ xi +x2-G21(1)) 4 G12(1)-2121) i (24 x1-G12(T))? | 72(x1 32,7) | ene { = S2@ y x2 +x1-G12(T), ee G2L(T)-21(7) (x1 +x2-621()" 3mP-xy diagram at T := (60+273.15)-K Guess: P := 70-kPa Given pm xteyl(xt 1-1, 1)-Psat (1) «. + (1 = x1)-y2(x1, 1 = x1,T)-Psatg(T) Peq(xl) := Find(P) xl-yl (x1, 1 ~ x1, 1)-Psaty(T) 0,0.05.. 1.0 vyeq(xl) := 0.05; ar a5 a2 | [ozs] 03] 035; oa 035 05 055) (8) 08s Or a76 08. 035 [09] 095) 372Pxxy Diagram at T = 333.15K 35 x. yeats) 12.15. It is impractical to provide solutions for all of the systems listed in the table on Page 460; we present as an example only the solution Tor the system f-propanol(1)/water(2). Solutions for the other systems can be obtained by rerunning the following Mathead program with the appropriate parameter values substituted for those given. The file .med reproduces the table of NRTL parameters on Page 460 and ludes the necessary Antoine coefficients, Antoine coefficients: 1-Propanol: Al 2 6.0692 BL = 3448,.66-K = Cl = 204.09-K Water: 6.2620 B2:=3799.89-K C2. = 226.35-K Psat) (T) SSH BUELL L (T= 273.15-K) +C1 | Psat(T) me | xp] A2~ le: @-273.15K) +2 Parameters for the NRTL equation: S081wa RT G21 (T) = exp(-a-221(1)) w21(T) = r \2 | G21) ] YUGL x2, T) = exp) x2’ | im So) “|| | G12(T)-12(T) | (2431-61201)? JJ of (_ 6am _Y | AGI Y2,T) = ep] a) e120) S| ,_21(1)21) | (xl +32.621(1))” J T-xy diagram at P := 101.33-kPa Guess: = (90 + 273.15)-K Given p= xleyl(xd,1 = x1, T)-Psath(T) +(1=x1)-y2(x1, 1 ~ x1, T)-Psaty(T) Teq(xl) := Find(T) xL-y1 (XE , | — x1, Teq(x1))-Psaty (Teq(x1)) ———eoo yeq(xl) = 3740,0.05...1.0 Teq(x) x= yea(x) = K a ° a8 0.05 oer 363.579 [23} 0.379) Set 715 0: 0.308 Fae 02 ‘0403 1035 025 ‘o.a08 30S 03: oai6' 308 036: 0.35 ore 04 0.436) 350882 045) 0888 380.64 05 0.68 360677 O55: O61 350767 08 ‘0507 35083 065 0828 Sa 07] 0865 SII O75 0588 362.18 08 083 Ba [08s] | 0.683) | 363.043] 08] o764 355.361 0.985 ‘0.888 357353 a 1 370.282 T.xy Diagram at P := 101.33-kPa 375 x, yeq(x) 37512.16 It is impractical to provide solutions for all of the systems listed in the table on Page 460; we present as an example only the solution for the system J-propanol(I)Avater@). Solutions for the other systems can be obtained by rerunning the following Mathead program with the appropriate parameter values substituted for those given. The file WILSON. med reproduces the table of Wilson parameters on Page 460 and includes the necessary Antoine coefficients. Antoine coefficients: 1-Propanol: Al == 16.0692 BI = 344866K Cl = 204.09-K Water: A2:= 16.2620 B2 = 379989K C2 = 226.35-K Bl ] Psat (T) := exp) Al - 51 __ fe ox @-m.isH+o1 |” Psata(T) = ex A - = lea (T= 273.15-K) + C2 Parameters for the Wilson equation: cm’ ° Vi = 75.14- v2 = 18.07 mol ‘mol aid 775.48 a2 = 1351.90.22 mol mol ny we N2_ of -al2 V1 oof 221 AL2(T) = exp] SEE A21(T) := exp! St : vi of 32) ey v2 RT exo AIT) ary YY G1 2,7) = SX2-A12(T) x2 #x1 = x-A21(T)) | Gt +32-a127)) oof-at{ AP Aan) 2O«L,x2,7) x14x2-A12(T) x2 +x1-A21(T))] (2 +x1-A21(T)) 376(a) BUBLP: 1 := (60+273.15;K xl: x2i= 1 ~xl Guess: P= 101.33-kPa, yl: y= i-yl Given yl-P = xl-yl(xt ,x2,T)-Psaty(T) ylty2=1 y2P = x2-y2(x1 ,x2,T)-Psat2(T) {Poul yl | := Find(P,yl,y2) 31,27kPa yl= 044 y2.= 0/586 Ans. ()DEWP: —T := (60+273.15)K yl P= 101.33-kPa xl = 0.1 Guess: Given yl-P = xt-yL(x1,x2,T)-Psaty(T) xl 4x25 y2P x2+y2(x1 ,x2,T)-Psatz(T) x1 = 0,042 x2= 0,958 Ans. (© P,T-flash Calculation Padew + Poubl = T:s (604273.15)K zl = 03 Guess: viens Ol x2i=1-yl yrs 0d yl t-xl Given x1-y1 G41, x2, T)-Psaty (TD) yl= 2 xt SL P x2-72(x1 ,x2,T)-Psata(T) ye tty 377xI(1-V)+yl-V= zl Eq. (10.15) xl x2 yl | = Find(xt ,x2,y!,y2,V) y2 Vv x130.08 x2=092 -y1-=.0.351_ y2= 0.649 -V = OBL (@ Azeotrope Calculation ‘Test for azeotrope at: T= (60 +273.15)-K 71(0,1,T) = 21.296 y2(1,0,T) = 4.683 «1129 = woes 112g = 21.696 Psat (7 a2} se xi) = 0.218 Since one of these values is >1 and the other is <1, an azeotrope e See Ex. 10.3(e) Gu P= 10133kPa x1 = 0.3 xis l-yl yl 03 ye Given yL-P = x}-71 (x1 ,x2,T)-Psat(T) y2P = x2-42(x1 x2, T)-Psaty(T) xl4x2=1 0 yl+y2= x2 yl ind(x1 ,x2,y1,y2,P) y2 \Paz Pag = 31,453kPa x15 04403 yl =0.4403 Ans. 37812.17 Its impractical to provide solutions for all of the systems listed ia the table on Page 460; we present as an example only the solution for the system I-propanol(1)/water(2). Solutions for the other systems can be obtained by rerunning the following Mathead program with the appropriate parameter values substituted for those given. The file NRTL.med reproduces the table of NRTL parameters on Page 460 and includes the necessary Antoine coefficients. Antoine coefficien L-Propanol: Al := 16,0692 BI := 3448,66-K Cl = 204.09-K Water: A2 == 16.2620 B2 = 3799,89-K C2 = 226.35-K BI ] Psaty(T) := exp] Al — ——_—____ ‘kPa a“ o[ (1 —-2B.15K) + Cl | B2 82 lips (P= 273.15-K) + C2 Psat(T) = cl 22 - Parameters for the NRTL equation: biz = 500.4024 bar = 1636.57 2 ‘mal mol bi2 1121) = Ot 217) G12(T) = exp(-a-t12(T)) G21(T) 35 exp(-a-+21(T)) r 2 7 yl (x1 x2) := exp! x27 221¢7) (ae) wl | x1 +x2-G21(T)) “| | i 4 G12 7127) | (2+x1-612(1)" = exp| x12] x12¢7) (22m } x2 +x1-G12(T), » @2L)-21(7) J Loa +22-G21(1))° 379(a) BUBL P: T= (60-+273.15)-K xis030 0 = I=x1 Guess: P = 101.33-kPa yl: 04 yl Given yl-P = xt-yl(xl ,x2,T)-Psat(T) yleyel y2sP = x2-y2(x1 ,x2,T)-Psatz(T) Pubt yl Find(P, yl ,y2) Ly Phub) = 30.98KPa yt $.0:397 y2= 0.603. Ans. (b) DEW P: T= (60+273.15)-K yl y2i=h-yl Guess: Ps= 101.33+KPa x20) Qe 1-x1 ee yL-P = x1-yl (X1,x2,T)-Psati(T) xl+x2= y2:P = x2-y2(x1 ,x2,T)-Psaty(T) Puew x ind(P,.x1 ,x2) x2 Page 2 207kPa xl = 0.037 x= 0963 Ans. (c) P,T-flash Calculation Pdew + Publ = Ts (604273.15)-K 21-03 Guess: Vv =05 yl 0.1 a xi-71 (x1 ,x2,T)-Psaty(T) Given eee xL+x22 1 P x2-Y2(x1 x2, T)-Psat2(T) ye ylay2=1 xb-(I-V)+ylV= zt Eq. (10.15) 380xl [2 yl | := Find(x1 ,x2,yl,y2,V} | ww xls 059 xQAO9I y= 0.345. y2= 0.655. V = 0.841 (@) Azeotrope Calculation ‘Test for azcotrope at: T := (60 + 273.15)-K IQ, 1,T) = 19.863 ¥2(1,0,T) = 4.307 1(0,1,T)-Psaty (7 aly = OED ESD e129 = 20.236 Psatz(T) Psat) (T) al2y = 20,0, T)-Psata(T) Since one of these values is >1 and the other is <1, an azeotrope exists. See Ex. 10.3(¢). Guess: P= 101.33-kPa xl yl x2 0. y2 Given yl-P = xl-yI(xl x2, T)-Psati (1) y2:P = x2-72(x1 x2, T)-Psatg(T) xl4x2=1 ylty2 xl=yl (x1 | x2 yl | = Find(xt ,x2,y1,y2,P) y2 (oa XI = 0.4204 yl = 0:4204 Ans, 38112.18 It is impractical to provide solutions for all of the systems listed in the table on Page 460; we present as an example only the solution for the system I-propanol(1)/water(2). Solutions for the other systems can be obtained by rerunning the following Mathead program with the appropriate parameter values substituted for those given. The file WILSON. med reproduces the table of Wilson parameters on Page 460 and includes the necessary Antoine coefficients, Antoine coefficients: L-Propanol: Al := 16.0692 BI = 3448.66-K C1 := 204.09-K Water: A2:= 16.2620 C2 = 22635-K Psat) (T) = exp) Al a Be Psat2(T) := exp} A2 - ————_—_______ |p ae. of 273.15 al . Parameters for the Wilson equation: 3 Vie 75:14 mol al2 ALT) = a on 2 ror y one AID) | aaa x1+x2-A12(1)_ x2 +x1-A21(T) }} YUGKL x2, 1) =a (x1 +x2-A12(7) eof{ 82 sic 201,27) = XL +x2-A12(T) x2 + x1-A21(T)}} (x2 + x1-A21(1)) 382(a)BUBLT: Pp 01.33-kPa xl :=03 x2:=1-x1 Guess: T= (60+ 273.15)K yl=03 yL-P = xI-yl (xt ,x2,T)-Psat;(T) yl+y2=1 y2P = x2-y2(x1 x2, T)-Psaty(T) oe jvt |= Find(T. 1.92) \ v2 Thub = 36L07K yis04i9 -y2= 0.581 Ans. (b)DEWT: P= 101.33-KPa yl 03 y Guess: T = (60+273.15)K xls 0.1 2 Given yl-P = xl-yl(x1,x2,T)-Psati(T) xl #32 y2-P = x2-y2(x1 ,x2,T)-Psatz(T) Taew | xl | := Find(T,x1,x2) 2) Tew = 364,29K xh = 0.048 32= 0.952) Ans. (©) PyT-flash Calculation Tew + Tou T oe P= 10133kPa 21 := 0.3 Guess: v=05 ee yl=01 x1-y1(x1 ,x2,T)-Psat(T) (Given fete y| tee eereen ne ep ee P x2-y2(ott x2, T)-Psaty(T) ee yl+y2=1 XL(I=V)+yl-V = zl Eq. (10.15) 3832 yl | := Find(xl ,x2,yl,y2,V) y v x1 = 0.089 x2=0911 yl= 0.35) (d) Azeotrope Cal ‘Test for azeotrope at: 101,33-kPa ro =[(—21_ cr) s27.15 Pp) Al = In| — KPa) Th2 := Ee = C2 | +273.15-K) 10,1 ,Tb2) = 16.459 71, 1,T)-Psat (Tb2) Pp PB 2,0,T) a2; : 2(Tb1) y2= 0.649 V = 0.805, TbI = 370.232K Th2 = 373.15K y2(1,0,Tb1) = 3.781 al2p = 19.598 ail2, = 0.282 Since one of these values is >I and the other is <1, an azeotrope exists. See Ex. 10.3(¢), Guesses: T= (60+273.15)K xl = 04 x25 yli=04 y2:=1-x1 Given yL-P = x1-y1(x1,x2,T)-Psaty(T) x1 #x2 = 1 y2P = x2-42(K1,x2,T)-Psaty(T) yl +y25 1 xleyl 38412.19 (xt) & YL | = Find(xt ,x2,y1,y2,7) Tez, Taz = 360,843K xls 0.4562 yl= 0.4562' Ans. It is impractical to provide solutions for all of the systems listed in the table on page 460; we present as an example only the solution for the system I-propanol(1)/water(2). Solutions for the other systems can be obtained by rerunning the following Mathcad program with the appropriate parameter values substituted for those given. The file NRTL.med reproduces the table of NRTL parameters on Page 460 and includes the necessary Antoine coefficients. Antoine coefficients: 1-Propanol: Al := 16.0692 BI = 3448.66-K Cl := 204.09-K Water: A2:= 16.2620 B2 = 3799.89-K C2 = 226.35-K seeneeiDleaaaaea |e (T=273.15-K) + C1 } a Psaty (T) = ol - B2 claee Psat(T) := exp] A2~ 2° __ a of (P= 273.15K) + 2 | Parameters for the NRTL equation: cal bi2 = 500.40 bat = 1636.57 0.5081 mol mol bi2 +12(T) = 2 b21 221(T) = —— RT Mae T G12(T) := exp(-a-112(T)) G21 (T) = exp(-a-r21(T)) 3852 ou) AGEL x2.T) 2 exp) 32 a(S |, gi2m-12c) L g2+xr-ciany? GIT) x1-G12(1) G21(T)-21(1) Eee Ate (xl 442-421 (1)? (@)BUBLT: P 01.33-kPa xl Guess: T= (60+273.15)-K yli= 03 Given yl-P = xl-yl(X1,x2,T)-Psati(T) yl+y25 1 y2eP © x2-y2(x1 ,x2,T)-Psatg(T) ( ee yl | := Find(T,yl,y2) ( ye Toobt = 360:81K yi= 0.416 y2= 0584 Ans (b)DEWT: P= 101.33-kPa yl = 03 y2:= 1-xl Guess: T = (90 + 273.15)-K x1 = 0.05 x2izl-yl Given yl-P = x1-7i(x1 ,x2,T)-Psaty(T) y2P = x2-72(x1,x2,T)Psaty(T) EZ I (Taew xl t= Find(T, x1 ,x2) x2 Taow = 364.28 xt = 0.041 Ans, 386(© P,T-flash Calculation Taew + Toubt 101.33-kPa zl := 0.3 2 Guess: x= 01 x2 1-yl yl = 0.1 y2:=1-xh I-y1. Gel ,x2,,1)-Psat (T) Given ys Sere re alee x2-y2(x1 ,x2,T)-Psato(T) ee yleyoet ey xI-(1-V)+yl-V = zl Eq. (10.15) x1) 2 yl | = Find(x1 ,x2,yl,y2,V) y2 v xf=0,069: x2=0.931 yl = 0353 y2=0647 V= 0814 (d) Azeotrope Calculation Test for azeotrope at: P := 101.33-kPa Tel = a = 0 +2nsx] ‘Vol = 370.232K Al-|h | . ( yo) ‘Tb2 = 373.13K V1 (0,1, 162) = 14.699 (1,0, Tb1) = 4.051 387yl (0, 1,T)-Psat} (Tb2 aly = P a2; = 0.271 21,0, 1)-Psata(Tb1) Since one of these values See Ex. 10.3(¢). Guesses: T= (904273.15)-K x1 =0.4 x2 >I and the other is <1, an azeotrope exists. yl yliz 04 y2 Given yL-P = xl-yl(x1 ,x2,T)-Psaty(T) x1 +92 = 1 y2P = x2-y2(X1,x2,T)-Psatg(T) yl +y2= 1 xleyl (x x2 yi ind(X1 ,x2,y1 2,7) y2 (Taz Taz = 360.641K xb = 0.4477 yl= 0.4477. Ans. 12.20 Molar volumes & Antoine coefficients: 74.05 14,3916 2795.82) (230.00 ) 40.73 16.5938 3644.30 C =| 239.76 18.07, 16.2620, 3799.89, 226.35 Bi Psat(i,T) := exp} Aj 7 lira (65 +273.15)K y 73. S)+ci | 0 161.88 291.27 583.11 0 107.38 |S i l4ago1 46955 9) ™ Wilson parameters: 388(a) BUBL P caleulation: No iteration required. x03 x04 ag 1x19 ix, T) = ex9{ 1 (“e vain) fy | XpA@.1,7) LF aiid | (eden | -y ,x, T)-Psat(i,T) Publ = 7 XY, 1) Psat(i,T) Pub Phubi = H17.6kPa Ans. (b) DEW P calculation: yi 03 y2= 0.4 yse byl nye Guess: xp 0.05 x02 © ages ta xpo ar P= Phun Given Poy = xy-7(1,x,T)-Psat(I, 7) Peyg = xg-7(2,x,T)-Psat(2,T) Peyg = x3-y(3,x,T)-Psat(3,T) Dx 1 {ox i \ x2 | = Find(xy ,x2,x3,P) | % (Paew 3890035: 0.188 Poy = 68.05KP2 ang Xo Paew +P (© PyT-flash calculati T= 33815K 403 04 23:2 1~2-2 Guess: V=05 Use x from DEW P and y from BUBL P as initial guess. Given Pry © x-y(1 xs T)-Poat(1 1) w= VWtyreV = Peyp © xo-y(2.x,T)-Psat(2, 1) xp(1~ V) #y2-V 5 20 Prys = x3-y(3,X,T)-Psat(3,T) x3-(1- V) +y3-V = 23 Dae V=0.677 Ans. 38012.21 Molar volumes & Antoine coefficients: Antoine coefficients: 14.3916 2795.82 230.00 16.5938} B:=| 364430] C:=| 239.76 16.2620 3799.89 226.35 Bi T= (65+273.15)K ——Psat(i,T) == exp] Aj- kPa (Z 2. is}+c,| NRTL parameters: K 0 03084 0.5343 0 184.70 631.05 0.3084 00.2994 222.64 0 -253.88 = mo 0.5343 0.2994 0 (1197.41 845.210 a Gi, = exp(-c, 5+ ae jena) (a) BUBL P calculation: No iteration required. x03 x= 04 xg = 1x1 x2 [ou G5,i¥) VG,x,T) == exp} 4 : ae YG 51 Prost =) si7G,x,T)-Psat(i,T) ys sree rene) Publ (0,525 [oar |: Phubl = 115:8kPa Ans. 391(b) DEW P calculation: yi03 yee 04 Guess: xj 5005 x2 Pout Given Poy = xp-y(1,x,T)Psat(1,T)Peyp = xo-y(2,x,T)-Psat(2,T) PaesrGaDPaGy Yael (x : x2 2= Find(x, ,x2,x3,P) % \Paow. 0.038 x= |.019 Pay 2689KPa ang 072) Pew +P (©) PyT-flash calculation: ~ bub me03 mi04 32 1-2-2 Guess; V:= 0.5 Use x from DEW P and y from BUBL P as initial guess. Given P-y, = xp-y(1,x,T)-Psat(1,T) xi(l-V)+yr-¥ 3 zy Pryp = xory(2,x,T)-Psat(2,7) x(1-V) +y2V = 2p Pryg = x3-7(3,x,T)-Psat(3,T) xa(1-V) +y3-V 1 yee a 392XL x2 X3 yi | 2= Find(xy ,x2,x3,1.92,93,V) y2 33 | i) foils 039i x=] 0346 y=} 0427 V-=0668 Ans. - \0.536. A0.182 12.22 Molar volumes & Antoine coefficients: 74.05 14.3916 2795.82 230.00 V:=|40.73| A :=| 16.5938] B= | 3644.30] C=] 239.76 18.07, 16.2620 3799.89, 226.35 Psat(i,, 1OL.33kPa 0 161.88 291.27 Wilson parameters: 583.11 010738 = mol 1448.01 469.55 0 AG,1,T) = —Lexp| Sed 3 3 4,1) @ of RT ) 7 (a) BUBL T ealeutation: x27= 0.4 X35 T= xy xg 393y(i,x,T) = expl 1 2 oy ete xpA(,i,7) rd jA@.j.1) Guess! T= 300K yy = 030 y= 03 yy= 1 -yl-y2 Given Pry = xp-y(1,x,T)-Psat(1, 7) Pey2 = xa-y(2,x,T)-Psat(2,T) P-y3 © x3-7(3,x,T)-Psat(3,T) Sx Psat(i,T) fm ve = Find(y1 y2,93,T) v3 Tub! ) (0.537 y=} 0.362 Tyuot = 333.97K Ans, 0.102. (b) DEW T calculation: y= 03 yo Guess: x1 1= 0.05 xp s= wietmyn xg 1-xy-x2 T= Thubt Given Poy = xy-y(1,x,T-Psat(1,T) Py = xp-7(2,x,T)-Psat(2,T) P-y3 = x3-y(3,x,T)-Psat(3,T) Dae 1 394f x1 © | c= Find(x1,x2,%3,7) fee. (teew ‘0.042 x= 0.203 Teow = 3474K Ans. (0.755 Tew + Tt (©) P.T-flash calculation: =e M03 m=02 yxl-y-m T = 340.694K Guess: V:= 0.5 Use x from DEW P and y from BUBL P as initial guess. Given Peyy = xpy(1,x,T)-Psat(1,T) xp(l-V)+ypv = 21 Peyg = xz-y(2,x,T)-Psat(2,T) x2-(1- V) +y2V § 22 P-y3 = x3-y(3,x,T)-Psat(3.T) x3-(1- V) +y3-V = 23 Ds Py x1 x2 x3 Yt | = Find(x1,x2.3,91,9293-V) 3950,124) 0:537 0.169 y=} 0.241 V.= 0.426 ‘Ans. 0.706, 0.222 12.23 Molar volumes & Antoine coeffici Antoine coefficients: 14.3916. 2795.82, 230.00 16.5938, B 3644.30 239.76. 16.2620. 3799.89, 226.35, P := 101.33kPa Psat(i,T) Ain i(epeacccatet) ate PkPa lk ~ 273, 33] +C NRTL parameters: K 0 0.3084 0.5343 0 184.70 631.05 ) a:=/0308 0 02994] bi=| 22268 0-23.88 | 0.5343 0.2994 0 1197.41 845.210 J ae i1.3 3 1 Pe 1i,j,T) = 3 GGT) = exp(-ai, 520.5.) (a) BUBL T calculation: x03 x04 x3 x1-¥2 YG... GGT 4 664.0% yGi,x,T) := exp] 2k. .-Gk.i,D) GG4,7) ( i | VS aD - pa 905.91 J 7 396Guess: T= 300K yp 0.30 yg 03 ysis ly -y2 Given Peyy = xpy(1,x,T)Psat(, 1) P-y2 = x2-7(2,x,T)-Psat(2,7) Pey3 = x3-7(3..x, T)-Psat(3,T) SY xvGx.7 Psat(i,T) (fu) yp = Find(y1,y2.¥3-1) Thubl = 334.4K Ans, (b) DEW T caleulation: y= 03 -yiny2 Guess: x1 = 0.05 xg = 1-x1-42 T= Thubi Given Py, = xpyCx,T)-Psat(l.T) Py: 2,8, T)-Psat(2,T) Pey3 = x3-7(3,x,T)-Psat(3,T) yx x1 i 2 = Find (x1 ,x2,x3,T) 3 Few. Tew = 347:5K Ans. 297Teew + Tbubl (©) P,T-flash calculation: T 5 T =.340.955K. ms03 202 1-2-2 Guess: V:= 0,5 Use x from DEW P and y from BUBL P as initial guess. Given P-y) = xy-y(1,x,T)-Psat(t,T) xp(l-V) +yrV = 21 Peyp = xo-7(2,x, T)-Psat(2,T) x(1-V) +y2-V = 2 Peys = x3-y(3.,T)-Psat(3.T) xx(1- V) +93-V 5 23 Sse! a ind (x1 ,x2,%3,y1,y2.95.V) (0.132 (0.537. *= | 0.173 0.239 V= 0415 Ans. 0.695, 0.224 39812.26 x xg 1x] ee VE = 7.92. mol mol VE 2= xy-x2-(45-x1 + 25-9] By Bg. (2227): Vie VE+xpVi txV2 Y= 1059250 ‘mol By Eqs. (11.15) & (11.16): Vbar) := V+x24_v Voar) = V-x;|¢-v ox ax; om om? Var; = 105,022 Vbary = 105.925 Ans a ‘mol ‘mol Cheek by Eq. (11.11): 3 V r= xp Vbary + x9: Vbar v=10592 ok mol moles) == eae em moles 1 82 moles; + moles? moles = 25.455mol moles), “1 x1 = 0.503 xzis d= moles: on? iy VE == xp-xp{ 1.026 + 0.220-(x} - x3) J VE = -0.256 5 mol mol By Eq. (1227), V5 VE+xy-Vy+x9-V2 V = 88.1369. mol Vioal ‘= Vemoles Vigat = 2243¢m° Ans. 39912.28 For an ideal solution, Eq. (11.78) applies: Veoeal = (x1-Vi +X2:Va)-moles Vital = 2250em? Ans. LiCL2H20 --> Li+ 1/2 C2 +22 +02 (1) Li+ 12 C12 + 10 H20 —> LiC\(10 H20) 2) 2(H2 + 1/2 02 —> H20) 8 LiC12H20 + 8 H20() --> LiCI(10 H20) 1012650)-3_ (Table C.4) 441579-5 (Pg. 444) (-285830-J) (Table C4) AH] + AH2 + AH3 5895 (On the basis of 1 mol of solute) Since there are if moies of soiution per mole of solute, the result on the HCW.S H20) 2.44 di mad 5 with sign changed12.30 Calculate moles of LiCl and H20 in original solution: 0.1-125 0.9-125 a= kmaol nyL0 kmol BUC "72.39 20 18.015 nic) = 0.295kmol ny20 = 6.245 x 10° mol 20 ; Moles of LiCl added: nic s= Gag'kmol ici = 0.472kmel nu Mole ratio, original solution: “22 — 91.18 ric 0 Mole ratio, final solution; = —~@°__ 8.15 ALicl+ 8LiCL ALicl-+ AL ic = 0.7667kmo! 0.2949(LiCI@1.18 H20) -—> LiCl + 21.18 H20) (1) 0.7667(LiCI + 8.15 H20 —-> LiCI(8.15 H20)) (2) 0.2949 LiCL(21.18 H20) + 0.4718 LiC > 0.7667 LiCl(8.145 H20) Au = nuci(3 ai (Fig. 12.14, n=21.18) mol) AH2 (aici + atic) (= ») (Fig. 12.14, n=8.15) mol, Q:= AHI + AH2 Q=S14213kI Ans. 12.31 Basis: 1 mole of 20% LiCl solution entering the process. Assume 3 steps in the process: 1. Heat M1 moles of water from 10 € to 25. C 2. Unmix 1 mote (0.8 moles water + 0.2 moles LiCl) of 20 % LiCl solution 3. Mix (MI + 0.8) moles of water and 0.2 moles of LiCl 401Step 3: Guess M1 and find AHS solution from Figure 12.14. Calculate AH for process. Continue to guess M1 until AH =0 for adiabatie process. (0.8:mol+ My) oy My := 1.3-mol 13 = ———___+ AHG = -33.16— 0.2-mol mol 3 = 10.5 AH := My-AHj ~ 0.2-mol-AH3 + 0.2-mol-AH3 AH = -0.061kI Close enough soem Ans, M+ T-mol 12.32 H20@5C 120 @25C€ (1) LiCIG H20) LiCl+3#20 @) LiCl+ 4120 LiCl(4 H20) GB) aH = 1.509 mol AH := 20756 From p. 444 (AH LiCl(s) - AH LiCl in 3 mol HO) mmol 255-1 Krom Figure 12.14 mol ‘AH := (AH) + AH + AH3}-0.2-mol ‘AH =:7646.9051 Ans. 40212.33. (a) LiCl+ 41920 —~-> LiCK4H20)AH := 2558 From Figure 12.14 ‘mol 0.2-mokAH =-5.1k) Ans. (b) LiCl H20) => LiCl +3 H20 (1) LiCIG H20) + 120. (s) - AH LiCl in 3 mot 11,0) cl AH = 20.756" From p. 444 (AH Lit -25.5-AL From Figure 12.14 ak 2 mol AH := 0.2-mol(AH; +A4Hp) AH =+0.949kJ Ans. Li+172. C2 +H2+ 1/202 (1) (c) LiC*H20 H2+ 1/202 @) Lit 12CR 8 @ LiCl + 4820 LiCK4 H20) YH20+3H20 - Li AH, = 712.58: x From p. 444 for LiCt-H,0 mol From Table C.4 AH, H,0() From p. 444 for LiCl AH From Figure 12.14 AH := 0.2-moh(AH; +AH)+AH3+AHg) AH =/-1472k) Ans. iC(4H20) (1) +9120) (2) (a) LiCl + 4420 4/9 (LiC(9 H20) 5/9 LiCl + 4/9 LiC9 H20) ——> LiCK4 120) 403ass From Figure 12.14 mol Ay = 4.324) From Figure 12.14 9 mol AM, AH := 0.2-mol(AH) +AHj) AH $-2.22k) Ans. LiCl +3 120) (1) LiCl +9 120) @) LiCI(4 H20) (3) \9 H20) > LiCl(4 H20) (©) 5/6 (LiCK3 H20) 1/6 (LiCI(9 H20) LiCl+ 420 5/6 LiC(3 H20) + 16 -20:156)- From p. 444 (AH LiCi(s) - AH LiC1 in 3 mol H,0) mol 32.4) From Figure 12.14 mol AN; := -25.5 From Figure 12.14 mol “U561K) Ans. AH := 0.2moh(AH; +4Hj+4H3) AH = ® 58 Lic*H20 LiH12 C2 +H2+1202) (dy 5/8 (H2 + 1/2 02, 20) @ 3/8 (LiC(9 H20) LiCl + 9 820) 8) 5/8 (Lit 12 C2 Lich @ iCl + 4 20 LiCK(4 120) 6) 'H20 + 3/8 LiC\(9 H20) —~-> LiCl(4 H20) 58. Aly = 2712.58) From p. 444 for LiCH1O. 8 mol (285.89) From Table C.4 AH, H,0() mol AH; = 2.02.4 From Figure 12.14 3 mol 404a : Hy = 5:¢-408,61y-AL From p. 444 for Lic 8 mol AHs := -25. 5 From Figure 12.14 mol AH := 0.2 mol (AH; + 4H) +4H3+AH,+AHs) AH =-0.403K Ans. 12.34 BASIS: 1 second, during which the following are mixed: (J) 12 kg hydrated (6 H20) copper nitrate Q) 15 kg H20 15 kmol m= BL 395.61 se0 2 ny = 0,041 Kel sec ‘Mole ratio, final solution: 6(H2 + 1/2 02 > H20()) o Cu + N23 02> Cu(NO3)2 @ ‘Cu(NO3)2.6H20 --> Cu+N2+602+6H2 — @) Cu(NO3)2 + 20.81 H20 -—> Cu(NO3)2(20.51 H20) (4) 120() —> Cu(NO3)2(20.51 120) ‘Cu(NO3)2.6420 + 14. AHL := 6-(-285.83-k)) (Table C.4) AH2 t= -302.9.K AH3 2110.8-K3) AHA = =47.84-kI AH := AHI + AH2 + AH3 + AH4 AH = 45.08kJ This value is for 1 mol of the hydrated copper nitrate. On the basis of 1 second, Qn Ae Ans. mol12.35 12.36 LiC13H20 —> Li+ 172 C2 +3H2+3/202 (1) 3(H2 + 1/2 02 --> F200) @ 2Li+ 1/2 C2 +8 H20 —> LiCIGH20)) 3) LiCK7H20)---> Li+12C2+7H20 (4) LiC\(7H20) + LiC13H20 —> 2 LiClSH20) BLL Sd AH2 := 3.(-285.83-k)) (Table C.4) (439.288) (Pg. 444) (-436.805-kI) AH AH = AHI+AH24AH3 +AH4 AH = 19.488KI Q=AH Q=19488k) Ans. Li+ 1/2 C2 + (0+2)H20 —> LiCn+2 H20) (1) 2(H2 + 1/2 02 --> H20) @Q) LiCL2H20 —> Li+ 1/2 CI2+2H2+02 — @) LiCL2H20 + n H20 —> LiCl(n+2 H20) -(-285.83-KJ) AHS := 1012.65-k} (Table C.4) Since the process is isothermal, AH = AHI + AH2 + AH3 Since it is also adiabatic, AH = 0 Therefore, AHI := ~AH2 - AH3 AHL = 440.991) Interpolation in the table on pg. 444 shows that the LiCl is dissolved in 8.878 mol H20, XLic 0.4012' Ans.12.37 Data: ne ~te-74 15 867.85 20 870.06 25 -871.07 nis] 50 ‘AH == | -872.91 |-kI 100 873.82 300 ~874,79 500 -875.13 1000. 875.54 Ca+ C2 +n H20 ---> CaC2(n H20) AHy Cals) --> Ca + C2 ~AH fea CaCh(s) + 0 H20 > CaCl H20) — AHtilde From Table C.4: AB goacy * ~795.8:KI ~-Tows(n) (“en Boe 4071238 CaCl > Ca+ CR w 2(Ca + C2 + 12.5 H20 ---> CaC2(12.5 H20) (2) CaC2@S H20)—> Ca+ C2 +2520 3) CaCRQ25 H20) + CaC2 --> 2 CaCi2(12.5 H20) AHI = 795.84) (Table C.4) AHO = 2(-865.295-K3) AHB := 871,07-K) AH := OHI + AH2 + AH3 Q=4H = Ans, 12.39 The process may be considered in two steps: Mix at 25 degC, then heat/cool solution to the final temperature. The two steps together are adiabatic and the overall enthalpy change is 0. Calculate moles H2O needed to form solution: 18015 e 34.911 Moles of H2O per mol CaC2 in final solution. 170.986 Moles of water added per mole of CaCl2.6H20: n-6 = 28911 Basis: 1 mol of Cacl2.6H20 dissolved CaC2.6H20(s) —> Ca + C2 +6 H2+302 (1) Ca + C2 + 34.991 H20 --->CaCI2(34.911 H20) (2) 6(H2 + 1/2 02 —-> H20) 3) CaCR.6H20 + 28.911 H20 > CaC2G4.911 H20) AHI := 2607.94 AH = 6-(~285.83:k)) (Table C4) AH2 := -871.8:45 (Pb. 12.37) ‘AHpog ‘= AH] + AH2 +AH3 for reaetion at 25 degC AHgog = 21.123 Moin 2= (110.986 + 34.911-18.015)-gm motn = 739.908¢m 408ry Cp = 3.28: Kg-degC AT = -8.702degC 12.43 mj = 150-b (E2804) Hye 2 Tb 100: %rmy + 25-%-m2 m +m), m3 = mj +m Q 12.44 Enthalpies from Fig. 12. AHg9g + Cp-AT T= 25-deg + AT 3-H ~ (my-Hy + my Hp) AH 298 aT: Msoln' Cp he 6:298degC Ans. mg := 350-lb (25% soln.) Hy = -23-222 (rig. 12.17) Ibm = 47.5% — (Final soln.) (Fig. 12.17) n= 05 1x, (60 % sotn) Hy = 20- me (pure #2804) Hy = 1082 (pure H20) a _ HE := H~(xi-Hi + xH) Ans, 12.45 (a) my == 400-16 sm = 178-lbq, Hys= 100. BEY Ibm 35-%my + 10-%mg my +m m3 := my +m (85% soln. at 130 degF) (10% soln. a¢ 200 deg) Hy i= 152-200 irs m (Fig. 12.19) = 27.39% (Final soln) BTU ben Hy = 41 (Fig. 12.19) 40912.46 12.47 Q:= ms-Hg ~ (m-H) + mH) (b) Adiabatic process, Q= 0. BO2SBTU Ans. mH] +mzH2 B (epee ai Hy = 1isa55TS 5 mn Prom Fig, 12.19 the final soln, wit about 165 degF. this enthalpy has a temperature of (feed rate) (Fig. 12.17 at 20% & 80 degF) 55: (Fig. 12.17 at 70% and 217 degF) Ibm {Slight extrapolation] x2 = 0.7 Hy = 1157.7-222 Crable Fe, 1.5(psia) & 217 deg] Ibn xpm Ib Ibn ig et pigs mete eo eee yy gaye x sec see Sania Qs my Hz + m3-H3 ~ my-H} = 208802 Ans. Mix m1 Ibm NaOH with m2 ibm 10% soln. @ 68 degF. BASIS: mg = Ibm, x3 = 0.35 my = Lb (guess) i Given my +my= mz my txymy = xp-m5 (im ums. ind(my ,m3) my = 0.385 Ibm m3 = 1.385Ibm 41012.48 From Example 12.8 and Fig. 12.19 Hy 478.7220 Bim my-Hy + myH, Bee m3 From Fig. 12.19 at 35% and this enthalpy, we find the temperature to be about 205 degF. First react 1 mol S03() with 1 mol H20()) to form 1 mol H2S04{): $03()) + H20()) --> H2S04()) With data from Table C. Alggg ‘= [-813989 — (441040 - 285830)]-J_ AH 9g = -8.712« 10° Mix 1 mol or 98.08 gm H2SO4() with m gm H20 to form a $0% solution, MH2S04 mp2so4 ‘= 98.08-gm so = os MH20 = Msoln ~ MH2S04 Data from Fig. 12.17: Hupsos = am [pure acid @ 77 degF (25 degC)] mn Hao = 45 ~ [pure water @ 77 degF (25 degC)] Heoin 0.5 (80% soln, @ 140 degF (40 deg C)} AH mix = Msoin Hsoin ~ ™H2S04-Hi2804 — MH20°HH20 AFyig = -18.145 kg BLU Ibm AH 9g + AH nix Msoin an12.49 my = 140-lbm xp 0.1S mp :=230'lbm 65 Te (Fig. 12.17 at 160 degF) -1022e (Fig. 12.17 at 100 deg) myx + my-x2 m3 = my +m x3 = 55.4% m Q + (pH) +mg-Hy Q:=-20000-BTU 3 _ G+ (myth + meta) m3 From Fig, 12.17 find temperature about 118 degF 12.50 Initial solution (1) at 60 degh; Fig. 12.17: BrU my 2 1500:Ibn xi = 0.40 93. TU Ibm Saturated steam at (atm); Table F.4: 1m3(imy) == my + m2 Hp = 1150.5 202 Ibm xy-my Hy + my-H x3(m) = Ha(m) aaa my +m m3{ma, mg := 125:lbm x3(mg) = 36.9% H3(mg) = -2 * y mn ‘The question now is whether this result is in agreement with the value read from Fig. 12.17 at 36.9% and 180 degF. It is close, but we make a second calculation: salma) 5.37% This is about as good a result as we can get. 41212.51 12.52 Initial solution (1) at 80 degF; Fig. 12.17: mj := Flbm xy = 0.45 Saturated steam at 40(psia); Table F.4: mg(mg) := my + mp Hy := 1169. BI Ibm xpmy som) = 2 mg := 0.05-Ibm x3(mg) = 42.9% Ha(m) = -34, sa ‘The question now is whether this result is in agreement with the value read from Fig, 12.17 at 36.9% and 180 degF. It is close, but we make a second calculation: BIU gle) = 5 .048-Jbim x3 (m) #42. This is about as good a result as we can get. Initial solution (1) at 80 degF; Fig. 12.19: my: Flbp: x1 = 040 Hy = 77-—— Saturated steam at 35(psia); Table F. Hy = 1161.12 x3 = 0.38 m2 = Ibm ms := my +m m3 = 1.053 ibm, my-Hy + m2-Hp m3 BTU We see from Fig. 12.19 that for this enthalpy at 38% the temperature is about 155 degF. 41312.53. Read values for H, Hi, & H2 from Fig. 12.17 at 100 degF: BTU Hz := 68-—— - Tom 12.54 BASIS: 1(bm) of soln. Read values for H1 & H2 from Fig, 12.17 at 80 degF: BTU BIU — HH = 48 =04 =1- Tbs 2 be x x2 x1 Q2 AHS H-xy-H)-xH)= 0 H = xy-H) +xz-H Hea See From Fig, 12.17, for a 40% soln. to have this enthalpy the temperature is well above 200 degF, probably about 250 degF. 12.55 Initial solution: —3¢j;= ———298.08 xy = 0.421 2.98.08 + 15-18.015. 3-98,08 3-98.08 + 14-18.015 Final solution x2 x2 = 0.538 Data from Fig. 12.17 at 100 degF: 414Unmix the initial solution: AB unix = [*1-Hin2sos + (1 ~ x1) He20 J - Ha AMypmig = 118.185 222 Ibm React 1 mol $03(g) with 1 mol H20()) to form 1 mol H2S04@), We neglect the effect of Ton the heat of reaction, taking the value at 100 degF equal to the value at 77 deg¥ (25 degC) 395720 -285830-— mol mol AH s03 J AH gaaso4 ‘= ~813989-— mol AH,x °= AHguaso4 — AHip10 - 4Hp503 AH, = -1.324x we mol Finally, mix the constituents to form the final solution: 137.23 BIL bm AH pi != Ho ~[s2Hipsoa + (1 x2)Haz0] AH mic Q Hynix’ (2-98.08 + 15-18.015):Ib ... + Llbmol- AH, .. + AH nig (3-98.08 + 14-18.015)-Ib @ 26809BTU Ans. 12.56 Read values for H(x1=' 1.65), HI, & H2 from Fig. 12.17 at 77 degF: Hex -125.BTU Hy = 0 BTU Tas Bin 65 41512.57 12.58 From the intercepts of a tangent line drawn to the 77 deg? curve of Fig. 12.17 at 65%, find the approximate values: Heer ee bag 103272 Ams. as ? Tbs Graphical solution: If the mixing is adiabatic and water is added to bring the temperature to 140 degF, then the point on the H-x diagram of Fig. 12.17 representing the final solution is the intersection of the 140-degF isotherm with a straight line between points representing the 75 wt % solution at 140 degF and pure water at 40 degF. This intersection gives x3, the wt % of the final solution at 140 degF: x3 = 42-% my := 1-Ib By a mass balance: 0.75-m} 0.75-m} tay i mem gO el (2) my = 25-lbyy im := 40-1 Serer x= 0 » eee Enthalpy data from Fig. 12.17 at 120 degF: Hy = 93 BU = 14.8 BTU Din bm — mg =m) +m +m3 mg = 1401bm xpmy + xyM2 + x3M3 xq = 0.42 (Fig. 12.17) Qs my Hy-(mpHy+me-H2+m3H3) QS=11055BTU Ans. 16(b) First step: mj :=40-1b mg == 75elb From Fig. 12.17 at this enthalpy and wt % the temperature is about 100 degF. BASIS: 1 mol NaOH neutralized. For following reaction; data from Table C.4: NaOH() + HCl(g) —> NaCl(s) + H20() AHg9g := [411153 ~ 285830 ~ (425609 - 92307)]-J AHagg = -1.791 x 10°5 NaOH(s) + HCl(g) —> NaClis) + H20() NaOH(inf H20) —> NaOH) + inf 20 (2) HCK9 H20) —> HCKg) +9 H20() 3) NaCl(s) + inf H2O -—> NaCl(inf H20) (4) NaOH (nf H20) + HCK9 H20) ---> NaCi(inf H20) AH) := Alg9g AH := 44.50-K3 AHs ‘= 68,50:KI AH = 3.88-kI AH = AH + AH + AH + AH, Qs AH 621871 Ans. 4712.60. First, find heat of solution of 1 mole of NaOH in 9 moles of H20 at 25 degC (77 degF). Weight % of 10 mol-% NaOH soln: Seas x1 = 19.789% 1-40.00+ 9-18.015 Hypo = sate (Table F.3, sat. lig. at 77 degF) Hola = asa 12.19 at x1 and 77 degF) Hyaou = 478. an [Ex. 12.8 (p. 455) at 68 degF] Correct NaOH enthalpy to 77 degF with heat capacity at 72.5 degF (295.65 K); Table C.2: 295.65-K molt = 40,00- mol Rr [ 16316-1075 BTU Cj 0.121 + BSN cp = 0.245 molwt | K Tbayrankine \ Hyaon = Hao + Cp-(77 ~ 68)-rankine HyaoH *= 480.91 x 0 AH := Hyoin ~ [x HNeor + (1 - x1)}-Hi20 | AH = 224 Thisis for 1 gm of SOLUTION. am However, for 1 mol of NaOH, it becomes: AH = 45.259 mol a8Now, on the BASIS of 1 mol of HCI neutralized: NaOH(s) + HCl(g) —> NaCis)+ 20) 4) HCl(inf 120) —> HC\(g)+inf #202) NaOH(@ H20) —> NaOH(s) + 9 H20 8) NaCl + inf H20 —>NaClinfH20) (4) HCIGinf 120) + NaQH@ H20) ---> NaCi(inf H20) AH == -179067-J. (Pb. 12.59) AH) 2=74.5:k) (Fig. 12.14 with sign ehange) AH := 45.259-kJ (See above; note sign change) AH4:= 3.88:kI (given) AH := AH) +AH)+AH;+AH; — Q:= AH 4049) Ans. 419Chapter 13 - Section A - Mathead Solutions Note: For the following problems the variable kelvin is used for the ST unit of absolute temperature so as not to conflict with the variable K used for the equilibrium constant 13.4 Hg) + CO2Ag) = H20(g) + CO) ve De By Eq.(13.5), yn, = yoo, -l-l+1+1=0 ng 1+ yH20 = yCO = By Eq, (A) and with data from Example 13.13 at 1000 K: T = 1000-kelvin e ) (395790) + £.¢-192420 - 200240)-—. mol! 2 ja fe. 2.082, po 2.084 ale) to® 2.086 2.088, ' 02, 03 06 42013.5 (a) H2(g) + CO2g) = H20(g) + CO) i By Eq. (13.5), +t T= 1100-kelvin (1-8) Jos I a = | —— ]-(-395' —— + =-(-187000 — 209110)-— .. G(e) \F Ic 395960) . 5 5 Peasy +RT otal ear) Guess: ee 0.5 Ans. Given 0.35,0.36..0.65, 2,102, 2.103 2.104 ole) 10° —2.105 2.106 213 O55 04 043 05055806 (0.65 at(by H2(g) + CO2(g) = H20(g) + CO(g) By Eq. (13.5), YH, > YCO, = T-1+1+180 ngs 1+152 =yco® = 7 yH20 = Yoo F > By Eq. (A) and with data from Example 13.13 at 1200 K: T = 1200-kelvin dey .4,0.41..0.7 -2.121 2122 2.123, Gle) 42(c) Hg) + CO%g) = H2O(g) + CO(g) » ¢D; AA= 542 AB = ~4.409x 10°? AC = 1.169%10°° AD = 83x 10° := 1100-kelvin ‘To := 298.15-kelvin 310°) = 897.285 wcrH(298.15,1100,3.542,-4.409.10" 9, 1,169-10 wwcrs(298.15,1100,3.542,-4.409:10"°, 1.169-107°,8.3:10°) = 1.78716 IDCPH := 897.285:kelvin — IDCPS := 1.78716 r AG = AH — Fy oss ~ AGpog) + R-IDCPH ~ R-TDCPS 43213.18 AG 2 -5.429% 10° Ken 2) K = 81048 mol By Eq, (13.28), = 0.5 (guess) a ie, (1s +6)-(.-8) By Eq. (13.4), noone Given ind(s) 5 = 0.83506 lte by = negHg = & ane yea = yo2Ha = 5H Te ee Vee Ite yeni yoons = 04551. ya 50.4552. Ans. (C2H5CH:CH2(g) = CH2:CHCH:CH2(g) + H2(g) vel oy (2) @) Number the species as shown. Basis is 1 mol species 1 + x mol steam. ng = 1+x 1 Texte From data in Table C.4, By Eq. (13.5), yi = 09730 mol AH p98 © ‘The following vectors represent the species of the reaetion in the order in which they appear: “1 1.967 31.630 =| 1 A= | 2.734 =| 26.786 |-10"7 1 3.249 0.422 873 0.0 Css | -8.882 |-107§ Di=| 00 |-10° 0.0 0.083. end := rows(A) iAA Dvesi AB = virB AC Yee AD =P vidi i i 7 i i! az 3x 10° AD BA = 4.016 AB = 4422x107? AC = 9.91x 107 ‘T := 950-kelvin ‘To := 298.15-kelvin iwcptt(298.15,950,4.016,-4.422-1073,0.991.1078,8.3-10°) = 1112511 10°) = 2.21675 wePs(298.15,950,4.016,-4.422-103,0.991-10"* IDCPH := 1112.51 1-kelvin IDCPS := 2.21675 AG := AHoo - 7 (AF29g — AG9g) + R-IDCPH - R-T-IDCPS 8G = 4.896% 10° K = 053802 mot By Eq. (13.28), ne Since 0.10-(1+x+e) = 0.843 f@) Ans. (b) Ans, 43413.19 C4H10(g) = CH2:CHCH:CH2(g) + 2H2(g) a @) @ Number the species as shown. Basisis | 1 4 1 mol species 1 + x mol steam entering. a 8 = —— = 0.12 14x42e ee ext de By Eq. (13.5), yy = y3 = 2y2 = 0.24 From data in Table C.4, i I = \— AG5g := 166365-— ‘Alagg = 235030-—— G298 = The following vectors represent the species of the reaction in the order in which they appear: =I 1,935 36.915 1 A= | 2734 B := | 26.786 |-107* 2 3.249. 0.422 j 11.402 0.0 6 5 -8.882 |-10 0.0 |-10 00 0.083, end := rows(A) iss Lend AA vv 297 AB = -9.285x10 9 AC = 252x107 +B Yc AD yy viDj 6 AD = 1.66% 10° 925-kelvin ‘To == 298.15-kelvin incpn(298.15,925,7.297,-9.285-10" 3,2.52-10" 1.66.10") = 1694.861 weps(298.15,925,7.297,-9.285-10"5,2.52-10" 5, 1.66-108) = 3.49109 IDCPH := 1694.861-kelvin IDCPS := 3.49109 AG T AHo9g — 7g (tase = AGo9) + RIDCPH - R-T-IDCPS 43513.20 AG = 9242 10° mol RT By Eq. (13.28), compa (inte) =K -e K Because O.12(1+x4+20) Be se K+(0.24) xh 20 x= 43151 € = 0.839 oR 1 @) y= Yaeam= 0.812 Ans. ) 1/2N2(g) + 3/2H2(g) = NH3(g) ve-l Basis: 1/2 mol N2, 3/2 mol H2 feed np = 2 ‘This is the reaction of Pb. 4.21(a) with all stoichiometric coefficients divided by two. From the answers to Pbs, 4.21(a), 4.22(a), and 13.7(a) ALL, DIVIDED BY 2, find the following values: J ~16450-—— ‘mol AB = 2,0905-107> AD = -0.3305-10° @ To s= 298.15-kelvin iocPH298.15,300,-2.9355,2.0905-10" 3,0.0,-0.3305-10°) = ~4.9576 imces(298.15,300,-2.9355,2.0905-10 40.0,-0.3305-10°) = ~0.016577 4.9576-kelvin IDCPS := ~0.016577 IDCPH := i AG := AHg9— Fy (Ass ~ AGo9g) + R-IDCPH ~ R-T-IDCPS 436aG = 1.627% 108 K = 679.37 mol Pl PO=t From Pb. 13.9 for ideal gases: pros e=l -(i + 1.299.K- F) 9664 PO} Yui = ya. = 0.9349 Ans. 2-6 ° 5 by the preceding equation (b) For ynH3 Solving the next-to-last equation for k with P = PO gives: K = 6.1586 1.299 Find by trial the value of T for which this is correct. It turns out to be 99:S-kelvin Ans. (©) For P= 100, the preceding equation becomes - K = 0.06159 129.9 Another solution by trial for T yields. “T+ (@) Eq. (13.27) applies, and requires fugacity coefficients, which can be evaluated by the generalized second-virial correlation. Since iteration will be necessary, we assume a starting T of 883 K for which: ForNu3Q): Tp= 8p, 21437 Pp Ip coger 405.7 12 PHIB(..43 ,0.887,0.253) = 0,924 43713.21 583 ForN2@y 0 Tes 335 PHIB(4.596, 2.941 ,0.038) = 1.034 For H2(), it is at such a large reduced temperature,that it may be assumed ideal; @ = 1. ‘Therefore, i 1.3 0.924) 1 =| 1.034 TT" = 0.909 1.000 i ‘The expression used for K in Part (c) now becomes: = K = 0.05598 [1299 (0.909 Another solution by trial for T yields T- 9K Ans. ‘Of course, the INITIAL assumption made for T was not so elose to the final T as is shown here, and several trials were in fact made, but not shown here, The trials are made by simply changing numbers in the given expressions, without reproducing them. CO() + 2H2(g) = CH30H(@) vez Basis: 1 mol CO, 2 mol H2 feed n= 3 From the data of Table C.4, 24791. mol This is the reaction of Ex. 4.6, Pg. 139, from which: AA 7.663 AB = 10,815-10°* AC = -3.45-10 © AD = -0.135-10° 438(@) T= 300-kelyin To = 298.15-kelvin incrti(298.15,300,~7.663, 10.815-10" 3, ~3.45-10" °,-0,135-105) = 9.043 weps(298.15,300,~7.663, 10815.10"?,~3.45-107, -0.135-10°) = ~0.03024 IDCPH := -9.043-kelvin IDCPS ‘= -0.03024 AG := AHQ98 ~ + (AH 29g - AGoog) + R-IDCPH ~ R-T:IDCPS 0 ) (ac ad AG 4 AG = -2.439% 108 — K = exp) K = 1.762% 10 e Peal owl aa J P =1 By Eq. (13.5), with the species numbered in the order in which they appear in the reacti e:=Find(e) © = 0.9752 (b) yz = 0.5 333 eis 2y3+t Solution of the equilibrium equation for K gives Find by trial the value of T for which this is correct. It turns out to be: T Aikelvin Ans. 439(c) For P= 100 bar, the preceding equation becomes 100°? K = 2.7% 10" 4(1-e) Another solution by trial for T yields T= 51648-kelyin Ans. (d) Eq. (13.27) applies, and requires fugacity coefficients, Since iteration will be necessary, assume a starting T of 528 K, for whiel 100 34.99 For COQ): T= Py = 2.858 PHIB(3.973,2.858, 0.048) = 1.032 100 Tr= 1.03 Py 512.6 80.97 For CH30H(3): T; := Py = 1.235 By Eq, (11.64) and data from Tables E.15 & E.16. 45 := 0.6206.0.97630°% 3 = 0.612 For H2(2), the reduced temperature is so large that it may be assumed ideal; 0 = 1. ‘Therefore: 1.032 4 =| 1.000 0.612 1 The expression used for K in Part (¢) now becomes: 3 (3-26) 4a(1—s) Another solution by trial for T yield 100" .0.593 K = 1.6011 x 107 S28 7ikelvin Ans. 4013.22 CaCO3(s) = CaO(s) + CO2%g) Each species exists PURE as an individual phase, for which the activity is £10. For the two species existing as solid phases, fand {0 are for practical purposes the same, and the ai If the pure CO2 is assumed an ideal gas at I(atm), then for CO2 the activity is (/10 = P/PO =P (in bar), As a result, Eq, (13.10) becomes K = P = 1.0133, and we must find the T for whieh K bas this value. From the data of Table C.4, Agog = 178321 a AGaog = todo) the order ‘The following vectors represent the species of the reacti which they appear: vl 12.572 2,637 3.120 1 6.104 | B= | 0,443 -107° Dd =| -1.047 }-10° 1 3.457 1,045, 1.157, 1.3 SA > iA B= SviBi AD =: Yer 3 4 AA = -LO1L AB = -1.149x 10 AD = 9.16« 10 298.15-kelvin 151.83-kelvin To ioceH(298.15,1151.83,-1.011,-1.149-1073,0.0,9.16-104) = ~1346.495 IDcps(298.15,1151.83,—1.011,-1.149-10"9,0.0,9.16- 104) = =1.86655 IDCPH := -1346.495-kelvin IDCPS := ~1.86655 Ee oi AG := AHy9g — Fy (Hoss ~ AGo9g) + R-IDCPH ~ R-T-IDCPS J ~AG) G = -126.353— K = exp( 2 = on( ar) Ke 1013 Thus Pes RR Ans, Although a number of trials were required to reach this result, only the final trial is shown. A handbook value for this temperature is 1171 K. 4st13.23, NH4CI(s) = NH3(g) + He) ‘The NH4CI exists PURE as a solid phase, for which the activity is 110. Since f and 10 are for practical purposes the same, the activity is unity. If the equimolar mixture of NH3 and HCl is assumed an ideal gas mixture at 1.5 bar, then with {0 = I bar the activity of each gas species is its partial pressure, (0.5)(1.5) = 0.75. Asa result, Eq. (13.10) becomes K (0.75)(0.75) = 0.5625 , and we must find the T for which K has this value. From the given data and the data of Table C4, 176013 Gogg = 91121 AHp§ mol ‘mol ‘The following vectors represent the species of the reaction in the order in which they appear: a 5.939 16.105 0.0 1 3578} Bi=| 3.020 }10°? D:=| -0.186 |-10° 1 3.156. 0.623 0.151 3 AA Deri AB yes ad =} vidi AA = 0.795 AB =~0.012462 AD = -3,5x 10° T= 623.97-kelvin Ty 298.15-kelvin wepH( 298.15 ,623.97 0.798 -12.462-10°3,0.0,-3.5-10°) = -1619.117 wcps(298.15,623.97,0.795 ,~12.462:10"3,0.0,~3.5-10°) = ~3.48845 IDCPH := -1619.117-kelvin IDCP! -3.48845 AG := AHg9g (AH29g - AGz9g) + R-IDCPH ~ R-T-IDCPS AG = 2.986 x 10° — K = 0.5624 Thus 7 $623.97K Ans. Although a number of trials were required to reach this result, only the final trial is shown. 48213.25 NO(g) + (1/2)02(g) = NO2(g) =-05 aeons 5 K 298.15-kelvin ywor(yo2)"* — ywo-(0.20) j From the data of Table C.4, AGaog #= ~35240-—— ‘mol (-a0 Keep ar K= 1.493% 10° yo = 10°? ywor = 107° (guesses) : 05 ee Given yno2 = (0.21)""-K-yno-ywo2 + ¥NO = 5-10) YNO Same ( } Find(yv0.yN02) io? \YNO2 This is about 7:107° ppm (a negligible concentration) Ans. 13.26 C2HA(g) + (1/2)02(g) = <(CH2)2>0(g) v= -05 See Example 13.9, Pg. 492-494, From Table C4, 3 J ‘AHg9g = -105140-— AGoqg <= -81470-— a9 eal 298 al Basis: 1 mol C2H¢4 entering reactor. Moles 02 entering: ng2 = 1.25-0.5 Moles N2 entering: BN? != No? 2 nig := 1+ng2+ nN? ng = 3.976 Index the product species with the numbers: trogen ‘The numbers of moles in the product stream are given by Eq. (13.5). 403For the product stream, data from Table C.1: Guess: g = 0.8 Ire 1.424 14.394 nog 0.5 3.639 0.506 |. 1973 B i le) e A= | 9385 23.463 | kelvin aN2 3.280 0.593 4,392 0.0 -1 0.0 6 227 0.5 12 D= -10° kelvin” = -9.296 | elvin? 0.0 1 0.0 0.040, 0 a4 Ale) = Yin): AG B(e) = > a(e):-Bi Cle) =F ale)ici DE) = ¥ale)edi n(e) os K(e) = 15.947 Me) on ogs ©) ‘The energy balance for the adiabatic reactor is: ‘AHg9g+AHp = 0 For the second term, we combine Eqs. (4.3) & (4.7). ‘The three equations together provide the energy balance. For the equilibrium state, apply a combination of Eqs. (13.11a) & (13.18).The reaction considered here is that of Pb. 4.21(g), for which the following values are given in Pb. 4.23(g) ‘AA := -3.629 .114:10°kelvin? To <= 298.15-kelvin Guess:B IDCPH : aato(e~1)+ Brg? -1) . +2fay 3.(3 ii wie) To \ 7 I IDEPS == AAdIn(t) +) AB-Ty +] ACT” ee ) -(r-1) aD (Ty | IDCPH = ~130.182kelvin IDCPS = ~0.417 Given Ble) * “AHlgog = R} Ale) To(e - 1) + 22 cle) DOs) + oOne le d. ig K(e) = exp| | S298 86298 | A298 ) | ncps - | RT) RTyt (ca) ©) _ (oss24s u aa F o) ares Ti=tTo ‘T= 949,23kelvin Ans. 13.27 CH4(g) = C(s) + 2H2(g) = 1 (gases only) The carbon exists PURE as an individual phase, for which the activity is unity. Thus we leave it out of consideration. 405,From the data of Table C.4, i 4 AH}9 := 74520-— A = 50460-— D9 a Case an ‘The following vectors represent the species of the reaction in the order in which they appear: 1 f 1.702 9.081 1 As] 1771 orn }-10-% 2 io 0.422 2.164 0.0 6 s 3 0.0 |:107 D:=| 0.867 |-10" 0.0 0.083 Desi AB Yves ac Svcs ad = S vidi : 7.01 x 10° AA = 6567 AB =-7466x 107? aC = 2.16410 AD = Ts 98.15-kelvin 23,15-kelvin Ty 1DcPHi(298.15,923.15,6.567,~7.466-10">,2.164-10°°,-7.01-108) = 1644.114 701-10) = 3.22848 wcPS{(298.15 923.15 ,6.567,~7.466-107>,2.164-10 ic = 1644.114-kelvin IDCPS := 3.22848 T AG := AHggg — Fp (olla = AGg9g) + R-IDCPH = R-TDCPS 0 -aG) aG=-11o9xwtt Ks onl 7 J} K=42302 mmol RT By Eq. (13.5), ng = 1 Ite (a) By Eq, (13.28), 448,0.7173 (fraction decomposed) 2e z: ae yeua = 0.1 ie Ans. () For a feed of 1 mo! CH4 and 1 mol N2, ng = 2 By Eq. (13.28), Given iat ats K Q+e)(-2) 250; (fraction decomposed) 13.28 1/2N2(g) + 1/202(g) = NO(g) veo @ ‘This is the reaction of Pb. 4.21(n) with all stoichiometric coefficients divided by two. From the answers to Pbs. 4.21(n), 4.22(n), and 13.7(n) ALL DIVIDED BY 2, find the following values: AH9g != 90250-—— AGagg = 86550-— mo mol ‘AA = ~0.0725 AB = 0.0795-10"* AD = 0,1075-10° T= 2000-kelvin Tp = 298.15-kelvin wcPHi(298.15,2000,-0.0725,0,0795-10">,0.0,0.1075-10°) = 62.763 icPs{298.15,2000, 0.0725 0.0795-10" 3, 0.0,0.1075-10°) = 0.036429 IDCPH 62.763-kelvin IDCPS == 0.056429 fr AG = AHa9g~ —~-(AFlagg ~ AGagg) + R-IDCPH ~ R-TIDCPS 0 “47aa =6s01xit@2 Ky ki x00( 29) Kj = 0.02004 mol \RT 1/2N2(g) + O2(g) = NO2g) 5 @ From the data of Table C.4, AH: = 33180- : AG: = 513102 298 °= mol 298 = mmol The following vectors represent the species of the reaction in the order in which they appear: 0:5 3.280 0.593 0.040 -t.| as|3039| B=} 0.506 |10°° 0.227 }-10 1 4.982 1,195, 0.792. ie.3 BASS vrAi AB =P viBi AD a Di AA = ~0.297 AB = 3.925% 10"* := 2000 -kelvin To := 298.15-kelvin wwcpH(298.15,2000,-0.297,0.3925.10 wwcps(298.15,2000,-0.297,0.3925-10" $,0,0,-0.585-10°) = -9.21904 IDCPH := 95.145-kelvin IDCPS := -0.21904 T AG := AHo9g — a (Hogg - AGz98) + R-IDCPH ~ R-T-IDCPS 5 AG = 1.592 10° mol ) Kp = 6.9373 x 10 With the assumption of ideal gases, we apply Eq. (13.28): JNO JNO 5 (@.7)95.(0.05)°% a) =k) 02)" 44813.29 yno #= K1-(0.7)°5.(0,05)"% Ans. @ Pont 200 yno2 -(t)" ei Ieee Ay GL a (yn2)"*-yo2r 0.7°4.0.05) PO ry 05 eepiaeneateo aes yor = (2) Kr (0.7005) non 4104 1Q"F Ans 2H2S(g) + $02(g) = 38(s) + 2H20(g) The sulfur exists PURE as a solid phase, for which the activity is £110. Since fand {0 are for practical purposes the same, the activity is unity, and it is omitted from the equilibrium equation. Thus for the gases only, From the given data and the data of Table C4, AH 98 # 145546 Gao = ~89830-2. mol mol The following vectors represent the species of the reaction in the order in which they appear: 2 3.931 1.490 0.232 5.699, og01 | -1.01 B :10"? Db * ha08 4.114 —1.728 0.783 2 3.470, 1.450 0.121 Sai AB Yves AD Ye AA = 5,721 AB = 065% 10°? AD = ~6.28x 10° 23.15-kelvin To := 298.15-kelvin 409,wmcpHi(298.15,723.15, 5.721 ,-6.065-10°°,0.0,-6.28-104) = 991.371 wees (298.15, 723.15,5,721,-6.065-10" 3,0.0,-6.28-10°) = 2.19811 IDCPH := 991.371-kelvin IDCPS » 2.1981] T AG = AHg9g — fs (AH298 ~ AGz9g) + R-IDCPH - R-T-IDCPS -1538x 108K exp AG mol By Eq. (13.5), gases only: ng = 3 ei=Finde) Percent conversion of reactants = PC niga) uJ “100 Tio mio PC 100 [By Eq. (13.4)] Since the reactants are present in the stoichiometric proportions, for each reactant, 100 PE76867" Ans. nip =v; Whence 13.30 N204(g) = 2NO2g) @ () Data from Tables C.4 and C.1 provide the following values: vel 030. mol J AH9g = 57200 AGaog To 2= 298.15-kelvin T = 350-kelvin 450AA = =1.696 AB = 0,133-107 AD := 1.203-10° ioceHi(298.15,350,~1.696,0.133:10" 3, 0.0, 1203-108) = -25.929 tHcPs{298.15,350,-1.696,0.13310 3,0.0,1.203-108) = -0.079402 IDCPH := -25.929-kelvin IDCPS := -0.079402 Be AG := AHy9g - To 3d AG = -3.968 x 10° — K=3911 mol = 2 = 0.4044 © = 0.7031 By Eq, (4.18), at 350 K: AH := AHggg + R-IDCPH. ait = 5694 mol This is Q per mol of reaction, which is .7031 — 0.4044 Whence Qs AltA 451xara | (1-xa)ya SATA SAYA 1331 By Eq, (13.32), In(ya) = O.1-xn” Infyp) = O.t-xa? Whence ae xp(0.1-x47 2 (seed Stl — XA “At a -exp[0.1-(2-x4 — 1)] K= eo 22) 1000. mol (guess) i (- 1 copfo.t(2xa—1)] = owl ee ) xa i= Find(xq) XA x, = 03955 Ans. For an ideal solution, the exponential term is unity: XA RT Given Find(xa) -#4'$'0:4005 ‘This result is high by 0.0050, Ans. 13.32 H20(g) + CO(g) = H2(g) + CO2%g) From the the data of Table C.4, AHg99 = ~41166-— mol To := 298.15-kelvin 482IDCPH := 539.735-kelvin [DCPS := 1.00107 AG = AHg93~ Flt = AGo9g) + R-IDCPH ~ R-TIDCPS AG = -9.668 10° K = exp 46 K = 4.27837 mol RT (a) No. Since v= 0 ,at low pressures P has no effet (b) No. K decreases with increasing T. (The standard heat of reaction is negative.). (c) Basis: 1 mol CO, 1 mol H2, w mol H20 feed. From the problem statement, f 2s ggn Tico + NH2 + NCOZ By Eq, (13.4), mpeite Neo =e Sere en Eg Oo Cte gig ae 6 = 0941 l-e+ltete 2+e 1.02 Let z= w/2 = moles H20/mole "Water gas”. By Eq. (13.5), yung = No# = 22=8 veo = 122 alte OS Daw 24dz Woo" oa 2e ye Free nes By Eq. (13.28) (guess) 2420 Given _#-(1+8) ao eK a Find Gia) z= Find(2) Ans. (@) 2C0@®) = COr®) +c) V==1 (gases) Data from Tables C4 and C.1: i ‘Aiggg := =172459.——— ‘AGy5g == ~120021-—2- mol mol 45313.33 AA= 0476 AB=0.702-10°> AD = -1,962-10° 1cPHi( 298.15, 800,0.476, 0.702-10" 3,0.0,-1.962:10°) = 19.511 wers{298. 15, 800, 0.476, 0.702: 10> 0,—1.962: 10°) = -0.12817 IDCPH := 19.511 -kelvin IDCPS := ~0.12817 AG := AH298 — % (F129 - AGz93) + RIDCPH ~ R-T-IDCPS, AG = -3.074 10" K= 1017 ‘mol By Eq. (13.28), gases only, with P= PO =1 bar yeor K= 101.7 for the reaction AT EQUILIBRIUM. (veo)? If the ACTUAL value of this ratio is GREATER than this value, the reaction tries to shift left to reduce the ratio. But if no carbon is present, no reaction is possible, and certainly no carbon is formed. The actual value of the ratio in the equilibrium mixture of Part (e) is yoo2 W232 yco = edn yeo2 = 0.092 yoo = 5.767 1075 x SiS psa RATIO := 2 RATIO = 2.775% 10° (sco)? No earbon can deposit from the equilibrium mixture. CO(g) + 2H2(¢) = CHBOH() ve-2 This is the reaction of Pb. 13.21, where the following parameter values are given: Aiggg == ~90135-—- AG 9g == -24791-— mol mol 550-kelvin To #5 298.15-kelvin 4546 AA = -1663 AB = 10815-1073 aC = ~3.45-107° AD = -0.135-10° 3 345-107 §,-0.135-10° ~3.45-10"°,-0.135-10° = ~956.435 2.39055 ICP H(298.15,550,~7.663, 10.815-107 swcrs(298.15,550,=7.663,10.815-10 IDCPH := -956.435-kelvin DCPS := -2.39055 AG := AHo9g ~ F(Attoos ~ AGg9g) + R-IDCPH ~ R-TIDCPS 0 ad -AG a = 3.339 10 — = exp, SO Ky = 6.749 x 10 AG = 3.339% 10" Ky oo( 2) 1 H2(g) + CO%g) = CO(g) + H20() v=0 (2) From the the data of Table C.4, I J ‘AHy9g := 41166-— G99 := 28618 — at, mol ae mol T= 550-kelvin To = 298.15-kelvin ‘The following vectors represent the species of the reaction in the order in which they appear: 1 3.249 0.422 0.083 -1 5.457 104s |g -hIS7} os vs 10"? D i 3.376 0887 =0.031 1 3.470, 1.450, 0.121 +4 AAS YS vidi a8 Svs AD = Y vidi AA = 86 AB=5.4x10°* AD = 1.164% 10° 0.0, 1.164105) = 231.996 0,1.164-10°) = ~0.540599 wcPH(298.15,550,-1.860,0.540-10 mDcPs(298.15,550,~1.860, 0.540-10~ IDCPH := -231.996-kelvin _ IDCPS := -0,540599 455t AG '= AHy9g— Fy (Atos = AGagg) + R-IDCPH - R-T-IDCPS 0 AG = 1.856% 108 Ky:= oo 2) K> = 0.01726 mol RT) Basis: 1 mole of feed gas containing 0.75 mol H2, 0.18 mol CO, 0.08 mo] CO2, and 0.05 mol N2. Stoiel metric numbers, vj; i= 2 CO CO2 CHBIOH = 20 i 1 2 al oO 1 0 2 a 1 -l 0 1 Eq. (13.7) 0.73 -2e)-€ 0.15 -e1 +22 eerste Seer = 2) 1 0.05 -€2 yoon® <> YeHOH = TE Pi= 100 By Eq. (13.40), 62:= 0.1 (guesses) Given e1-(1-2€;) > See ee (2) (0.7526) ~52)"(0.18-e,+e2) 0.15 ~ 1 + €2)-€ a ( 22 = Kp == Find(e; 29) “£1 ~ 8}-(0.05 -&) £ 5) = 0.1186 62 = 8.8812 10> 486O.1S—e; +82 0 Rey e) YCH3OH 28 ~ YH2~ YCO ~ Yoo? = YCH3OH ~ YH20 vis os 13.34 CH4(g) + H20(g) = CO(g) + 312g) v=2 @) From the the data of Table C.4, J J 205813-—— AGp9g := 141863-— mol 298: mol The following vectors represent the species of the reaction in the order in which they appear: AH29g 1 1.702 ‘9,081 = 3.470 1430] a 1 3.376 0.557 3 3.249, 0.422 2.164 0.0 29 ha ON 08 i l.4 00 ~0.031 0.0 0.083 AA meee AB ze AA=7.951 AB = ~8.708x 10"? * AD = 9.7% 10° 1300-kelvin1ocpHi(298.15,1300,7.951,-8.708:10"°,2.164-10° °,9.7-108) = 2585.215 rcps(298.15, 1300,7.951,-8.708.10°3,2.164.10"8,9.7-10°) = 4.76801 IDCPH := 2585.215kelvin DCPS == 4.76801 AG := AHygg - Z(sit08 = AGooq) + R-IDCPH = R-T-IDCPS 0 3 J -aG G = 1,031 10° Ky = exp 3S Ky = 13845 femal 7 ox #8) : H120(g) + CO(g) = H2(g) + COX) v=0 @ ‘This is the reaction of Pb. 13,32, where parameter values are given: roceri( 298.15, 1300, 1.860,-0.540-1073,0.0,—1.164-108) = 1130.273 scPs(208.15, 1300, 1.860, 0.540: 107 ,0.0,-1.164:10°) = 1.577615 IDCPH := 1130.215-kelvin IDCPS. 1.577615 AG <= AHy9g - Fy lone — AGyog) + R-IDCPH — R-T-IDCPS AG = 5.891 x 10° Ko on 22) mol RT (a) No, Primary reaction (1) shifts left with increasing P. (b) No, Primary reaction (1) shifts left with increasing T. (©) The value of K1 is so large compared with the value of K2 that for all practical purposes reaction (1) may be considered to go to completion. With a feed equimolar in CH4 and H20, no #20 then remains for reaction (2). In this event the ratio, moles H2/moles CO is very nearly equal to 3.0. 458(@) With 120 present in an amount greater than the stoichiometric ratio, reaction (2) becomes important. However, reaction (1) for all practical purposes still goes to completion, and may be cousidered to provide the feed for reaction (2). On the basis of 1 mol CH4 and 2 mol 120 initially, what is left as feed for reaction (2) is: 1 mot H20, 1 mol CO, and 3 mol H25 Thus, for reaction (2) at equilibrium by Eq, (13.5): CO = YH20 By Eq. (13.28), one 2048 a (1-ey YH? Ratio = Ans. Yoo (@) One practical way is to add CO2 to the feed. Some H2 then reacts with the CO2 by reaction (2) to form additional CO and to lower the H2/CO ratio. (D 2CO(g) = CO2%g) + Cis) vy =-I (gases) ‘This reaction is considered in the preceding problem, Part (d), from which we get the necessary parameter values: 120021 mol For T= 1300 K, 1300-Kelvin Ty := 298.15-kelvin wwcpH(298.15, 1300,0.476,0.702-10"3,0.0,-1 962.105) = 531.734 iwcps(298.15, 1300,0.476,0.702-10"3,0.0,-1.962-105) = 35870 IDCPH := $31.734-kelvin IDCPS := 0.35870 T AG = AHyo3 — Ps (A#295 - G98) + R-IDCPH ~ R-T-IDCPS 0 489oN : aG=s6nxitL Ks onl SG) Ke 52sscoux 1073 mmol RT) As explained Problem 13.32(d), the question of carbon depo: IAL compositions the value of this ratio is greater than the equilibrium value as given by K, there can be no carbon deposition. ‘Thus in Part (@), where the CO2 mole fraction approaches zero, there is danger of carbon deposition, However, in Part (d) there can be no carbon deposition, because Ratio > K: eS Ratio Ratio = 0.924 (2? 13.37 Formation reactions: C+ 282 = CHS C+ (12)02 = CO C+02=CO2 Elimination first of C and then of O2 leads to a pair of reactions: CH4 + #20=CO+3H2 (1) CO+H20=CO2+H2 @) ‘There are alternative equivalent pairs, but for these: Stoichiometric numbers, v5, CH4 #20 CO COP 2 VyFor initial amounts: 2 mol CH4 and 3 mol H2, n0 = 5, and by Eq. (13.7): 2-8 3-e)-e) 81-8, YCH4 = 5426) YH20 = Fe2e, Yco = TeDe ne Be) +82 Pete Eo gu mae Sd By Eq. (13.40), with P = PO=1 bar 3 yoor(yna)" yori _ ae ki om ek YCH4-YH20 YCO"YH20 From the data given in Example 13.14, J ‘AG, = =27540-— 8G; = 31304 1000-kelvin mol mol : -AG, } : -AG2 ieee aT) 2S OPT Ky = 27.453 Kp = 1.457 eels eg i= (guesses) Given (e1=#2)-(52) 403)? ~81)(3-e) -82)(5 +21) £9-(3€1 +22) =K (r= 8) 08-2) 1) | = Find(, ,e) e) = 1.8304 82 = 0.3211 £2) e~e e182 YH20 yco 5+ 26 3426) 461£2 eine a 5428 S42e) yous = 00196. 0.098 yoo = 0.1743 oo = 0.0371 yp = 0.671) ‘These results are in agreement with those of Example 13.14. 46214.1 (b) Chapter 14 - Section A - Mathcad Solutions Aya = 0.59 Agi = 142 T= (55 +273.15)-K Margules equations: rast) = expl (1-1) Aig +2(Aar - Ara)xr] | 2 1 sraler) = expL x1? Aas +2-(Ai2 ~ Aas)(1-x1)]] Psaty := 82.37-kPa Psatz = 37.31-kPa BUBL P calculations based on Eq. (10.5): Pauta(s1) := x1-7a(x1)-Psats + (1 x1} 72(s1)-Psata rvs} Pa Js nba = ae xp = 0.25 sisi): xy = 0.50 wba) xy 075 Phubilti) = 85.70 kPa vile) = 0.808 BUBL P caleulations with virial coefficients: 3 om 3 pe Baa = -1523- By == -963- mol mol 612 = 2-Bi2— Bui ~ Baa fr 2. | Bi-{P = Psat) + P- 04(P.7 91.7) = em zl “) ~ (PT. 91,92) 1 Bop-(P ~ Psat) + P-y1?-8 4 | ae RT 463Psat; + Psat 2 xy = 0.25 Given yt-® (PT, y1,92)-P = xr-yi(xi)Psaty yo@2(P,T,y1.y2)-P = (1 x1} 72(xs)- Psat Guess: yrs 05 yeloy y yz | = Find(y1.y2.P) bas x1 = 0.50 Given yi) (P.T.y1.y2)-P = x74 (x1)-Psaty y2@2(P.T y1sx2)P = (1x) ra(ui) Psst nel-y vt yo | = Find(y1 .y2.P) P xp=0.75 Given yr@ (PT, ys.y2)}-P = x1-74(x1)-Psati y22(PT yty2)}P = (1 x1) va(a1)Psate yeloy He iW ei y2 | == Find(yy .y2,P) P 46414.3 14.4 T= 200K Hy = 200-bar Assume Henry's law applies to methane(1) in the liquid phase, and that the Lewis/Randall rule applies to the methane in the vapor: fhaty! = Hy-xy ‘that; By Eq. (11.35): os on(22) $1 = 0.827 \ Equate the liquid- and vapor-phase fugacities and solve for x1: yee? : ee oni’ Ans. Ai Pressures in kPa. a Data: 0,000 12.30 0.000 0.0895 1551 0276 0.1981 1861 0.4565 0.3193 21.63, 0.5934 0.4232 2401 0.6815 0.5119 25,92 0.7440. 0.6096 27.96 0.8050 0.7135, 30.12. 0.8639 2..r0ws(P) xg: 1-x1 Psatz := Py (a) It follows immediately from Eq, (12.10a) that: ii) = Az ‘Combining this with Eq. (12.10a) yields the required expression 465(b) Henry's constant will be found as part of the solution to Part (c) (c) BARKER'S METHOD by non-linear least squares. Margules equation, ‘The most satisfactory procedure for reduction of this set of data is to find the value of Henry's constant by regression along with the Margules parameters. ‘yal x2,A12,Aa1) = expl 62)? Ana +2-(Aat ~ Aia)xt] oli x2,A12,Aa1) = expL_(1)2L Ani +2(Ai2 ~ Aoi)? || Guesses: 02 A048 Mininize the sums of the squared errors by setting sums of derivatives equal to zero. Given ‘ fel Hy 2] 0 | sale-(o (x1, Aa. A2I) Tae) : L (439; %2(%1, 3,12, A01)-Psate Hy | Pim] mira (a,o% Ai2,A21) #92, *72[81,0%2, ,A12,Aal) Psaty paris, siete) ty r sae exp(Aiz) +4) 2(81,%2,,A12,Aa1) Psat Ans, 466(a) y1(x1 x2) nol 2?[ Ar2 +2-(Adi- Av)xt]] 4220x1522) = exp x17 Agr +2-(At2 ~ Ant] } Hy Peas, = 1, 71( 1,984) AD +2 72(m1, 99,}Psata 02 ° Pious, _ “02 {oi vet) 100 -04 “06 ° 02 oa 06 08 x Xx Pressure residuals © yl residuals Fit GE/RT data to Margules eqn. by least squares: i= 2..rows(P) =>é Lia Given“expla ¥2;Pi +x9,Inj ——— ne, AQ Ans. Agr | s= Find(Ai2.Az1 Hi) Hy YUG&L x2) = exp] x2 Ar2 +2¢(Ag1 = Arz}ext Y2G.1 x2) = expl x1? Ag) #2-(Ai2~ Ani }2]] H, Peal © x1;71(1,-82)) ale) 2,721. My n(x Hi - a ‘Ai2) Peale, Yieale, 4680 02 04 06 08 x1 XX Pressure residuals © yl residuals 145 Pressures in kPa 0.3193 21.63 0.5934 Data 0.4232 24.01 0.6815 0.5119 25.92 0.7440 0.6096 0.8050 0.7135 30.12 * | 0.8639 0.7934 31.75 0.9048 0.9102 34.15 0.9590 1,000 36.09 1.000 i= 1.7 ” xi Psaty = Pg (a) It follows immediately from Eq. (12-10a) that: Combining this with Eq. (12.10a) yields the required expression. {b) Henry's constant will be found as part of the solution to Part (c). 468(©) BARKER'S METHOD by non-linear least squares. Margules equation. ‘The most satisfactory procedure for reduction of this set of data is to find the value of Henry's constant by regression along with the Margules parameters. ta(xl.92,A12,Aai) sp (2) Aiz + 2(Aa1 ~ Ata) xt} 5 roll .x2, Az, Ann) = exp 1) Agr +2-(A12- Ani) x2] | Guesses: Ho:= 14 An = 0.148 Ayz = 0375 Mininize the sums of the squared errors by setting sums of derivatives equal to zero, Given 0= 2. = 12 ! | 0 Elsa Pi = (11 (¥1,.%9,.412,A2i} eat | Heat Sapnafsypss Aina Ty d 7 | Pi- (xara (s1,.%2,-A12,Az1}-Psaty .. Taf fan foyrpaiots ra H2 so n(s.9, Ara Ane || Ad (Ar Az) 0.469 | Agr | := Find(Ay2,A21,Hp) | Aoi} =| 0.279 | Ans, (ie He}, 3487 (8) yl0at x2) = expl x2°[ Ara +2-(Aot~ Avz}xt] | y2(x1,,x2) = exp| x12. [Aa +2-(At~ Aat)22]] 470} Hp pPssts +9339(81, 2) Sota : i'l! exp(Aat, xi (x 2¥2)) Paty Peat, = 1,71 (X1,.%2, Veal = cua Peat ‘The plot of residuals below shows that the procedure used (Barker's ‘method with regression for H2) is not in this case very satisfactory, no doubt because the data do not extend close enough to x1 = 0. 1 oe Pi-Peale, 4 ° (21,-¥1teate)} 100, . 3 “oz 04 06 08 a xx Pressure residuals & yl residuals Fit GE/RT data to Margules eqn. by least squares: i. yo t-y ( vi;Pi ) xin] ——} — (Aatx, raya, Tl xp -Psaty | i 172 me) FAD, 4amviyPi ; ~ (Aare, oii sym }- ; S|) X1 0 Dia ex Psat ven ' 32, Pi Ha expan +39, An - Agi | = Find(Aj2,Az1,H2) Ho Get x2) = exp 2? Ara +2(Aa1 = Arg}! | 12Gs1 x2) = expl_ x17 Any +2412 ~ Ari)92] | Hz 1 11 (10%, Psat) +9,77(4,) Sota) x1 719% Psaty Yleale, = Peak, 47207 x %ox Pressure residuals’ © yl residuals ‘This result is considerably improved over that obtained with Barker's method. 14.6 Pressures in kPa Data: 15.79 0.0 0.0 17.51 0.0932 0.1794 18.15 0.1248 0.2383 19.30 0.1757 0.3302 19.89 0.2000 0.3691 P x 21.37 0.2626 0.4628 24.95 0.3615 0.6184 29.82 0.4750 0.7552 34.80 0.5555 0.8378 42.10 0.6718, 0.9137, i 2..rows(P) x= 1-1 Psat = Py (a) _ It follows immediately from Eq. (12.10a) that: inn?) = Ai Combining this with Eq. (12.108) yields the required expression 473(b) Henry's constant will be found as part of the solution to Part (c) (©) BARKER'S METHOD by non-linear least squares. Margules equation. The most satisfactory procedure for reduction of this set of data is to find the value of Henry's constant by regression along with the Margules parameters, Ayo +2(Ao1 ~ Arg)xt J] An}2 |] 127 Ay? = -0.70 yi (xt x2,A12.Aa1) = exp (22) sa(61 x2, Ar2,Aag) 2 exp 1)? Agr + 2-(A2 Guesses: Hy = 35 Art Mininize the sums of the squared errors by setting sums of derivatives equal to zero. Given > | rtm [ +439, 7o(81,0%2,.A12, Aa): Ponts oe Hy " nadie dal) (+2, Y2(X1, 982, Ar2,Azi) Psat Az) (0.731). AQ | = | 1187} Ans. Hi) (32.065 474,(8) yiGxt x2) == exp] x2 LAr +2-(Ao1 - Ars) xt ]} {20% x2) = expl x12 Ay +2(Ar2 ~ Ant)x2]} Peale, = s(t + x2,72( x1, »%2,} Psata Hy a, ¥1(s1,.%9,) zolan) Yieale, : Pose Wie) 0 01 02 03 04 05 06 029 x; X** Pressure residuals © yl residuals GEIR data to Margules eqn. by least squares: i= 2..rows(P) Given d aan 475fale Een ina . “I Sxp(Aia) 13; +x2,"Inl = x2,-Psatz Al Aal AL y(n) x2) = exp] 2°{ Ai +2(An1 - An)xt] 72(K1,,x2) := exp xi? Ag) +2.(A12~ Adi) 2]] aati ee + x2-72(x1_.x2, -Psaty TNO) Say tT) 476PjPeate, es Gat 0 01 02 03 04 05 06 07 x, Xx Pressure residuals © yi residuals 14.7 Pressures in kPa 0.1737 1930 0.3302 Data: 0.2000 19.89 0.3691 0.2626 21.37 0.4628 0.3615 24.95 ools4 0.4750 29.82 0.7552 MS) 95555 34.80 "| 08378 06718 42.10 0.9137 0.8780 60.38 0.9860 0.9398 6539 0.9945 1.0000, 69.36, 1.0000, i= 1.9 xg i= 1-xy Psaty := Pig (a) It follows immediately from Eq, (12.10a) that: Combining this with Eq. (12.10a) yields the required expression. (>) Henry's constant will be found as part of the solution to Part (c). a7(©) BARKER'S METHOD by non-linear least squares. Margules equation. ‘The most satisfactory procedure for reduction of this set of data is to find the value of Henry's constant by regression along with the Margules parameters. ult x2,A12,Aa1) = exp], 22 Aja +2-(Aat ~ Aig} xi] sraletx2A12, Anu) = exp] (x17? Ani +2(Ai2~ Aai)22 J] Guesses: Ho=4 0 Agy=-137 Ai = 0.68 Mininize the sums of the squared errors by setting sums of derivatives equal to zero. Given x4, 70 (81,992, ,A12-Azr) Psat y S-/ vr | dang i | l P va(*i, 2x2, A125 Ani) ) plan) } 478(@ 71Cxt x2) = exp| x2? A1+2-(Aat- Aa)xt]] 20st x2) := exp] x17[A21 +2-(Ar2 = Azi) x2] | Hp Peate, = X1p71(X1,.%2,) Psat + ¥9,72(%1,0%2,) onland xiv (11,2) Psat} Yicale, = ' Prato, 1 Pi-Peate Osea ce oe xx x Gives) 190 eee a ae oO 02 04 06 08 1 x, **<* Pressure residuals: © yl residuals Fit GE/RT data to Margules eqn. by least squares: i 1.9 yost-yt [(( ow \ ? xi tn Paar ||| Pst | +39,-ln| — | », | \ ) J 473yiyPi | : it xia fa fAara, «ap, i al ee . yaP x2 Aa Ho AG x2) = exp) 2A +2(A21-Arz)at || 2061 32) = exp] x1°[ Any +2(Ara~ Ani) ] | u, Peat 2= 8111 (s1,.¥2,) Psat 939/765, Ta xii Yteale,x; Xxx Pressure residuals © yl residuals 14.8 (a) Data from Table 12.1 15.51 0.0895 0.2716 (1304 1.009 18.61 0.1981 0.4565 1.188 1.026 21.63 0.3193 0.5034 4a 1,050 24.01 0.4232 0.6815 1.071 1,078 25.92 |kPa xj =| 0.5119] yi =| 0.7440} yy =| 1.044) yp := | 1.108 27.96 0.6096 0.8050 1.023 1.138 30.12 0.7135 0.8639 1.010 1.163 31.75 0.7934 0.9048 1.003 1.189 34.15 0.9102 0.9590, 0.997 1.268, ncsrows(P) oo n=9 i= lan Psat; = 36.09KPa Psat == 12.30KPa T's (50-4 273.15)K Data reduction with the Margules equation and Eq. (10.5): vii ¥2,Pi Pe Y: yi xy Psat 3 Xo Peat 481on GERT; = x1;ln(11,) 32, nfra, Guess: AO A= 03 = 7 [GERT- (Aarxi, + Ata-x2,) «1,2, £(A12,Aar Ai2) ( | :=Minimize(f,A12,421) Aig = 0374 Aap $0197 Ams. Agi) y | GPRT}—(Aarm, tara RMS Error: RMS =: (RMS = 1,033 107 x1:= 0,001.1 GERT, goo 0.05 [Aarxt+aye- (xt) Jot (at) Data reduction with the Margules equation and Eq. (14.1): 3 3 Bu=-18402- By =-18008. By mol mol 812 #= 2-Bj2- Bi — Bao flex = Psat) + Po(va)*9r2 | Er esi ta) a RT i 482Guess: A= 01 Ag = 03 £(A12,Az1) = 3 [GERT:~ (Aor x1, +Anz ist (Aw := Minimize(f,A}2,A21) ANZ (4a RMS Error: RMS := GERT; goa [aorxt+aqa-(-xt) }xt-l-xt) ‘The RMS error with Eqn. (14.1) is about 11% lower than the RMS error with Eqn. (1 483,Note: The following problem was solved with the temperature (I) set at the normal g point. To solve for another temperature, simply change T to the approriate value. 14.9 (a) Acetylene: Ty 2=308.3K Pg = 61.39bar Ty = 189.4K ie les T, = 0.614 2 = 0.08664 Y = 0.42748 Table 3.1 = 2a? Table3.1— a(T,) = ¥ atte < kg. (3.42) c Wa(T) Q a(t) = a7) bg sn) B(TrsP,) := Eq. (3.50) aT; Define Z for the vapor (Zv) Guess: Given Eq. 3.49) zw~B(Tr,Pr) zw ® 14B(T,.P,) -a(T,)-B(Ty,P, WreBiP)\@veo8cr) Zx(Tr.Py) Define Z for the liquid (ZI) Guess: zl:= 0.01 Find(zv) Given Eq. (3.53) a= B(T,,P,) + (21+ 6-B(Tr,Pe) {el 0-8 (Ty.Py gate) To find liquid root, restrict search for zl to values less than 0.2, zi < 0.2 “il, ,) Pind(zl) 484Define I for liquid (11) and vapor (Iv) 1 ZA(T, Pr) +o-B(TesP,) 1(Tr.P, a (a = ee (a9) ee-(t- 2) Eq. (6.62b) Z(T,.P,) +o-B(T;,P,) WP) = of ees ay Ingi(T; Pr) = Zi(Ts,Pr) — 1 - In(Zi(Tr,Pr) — B(Tr.Pr)) ~ a(Tr}-1U(Tr.Ps) Eq. (11.36) Ingv(T, ,P,) := Zv(T;,P,) ~ 1 ~ In(Zv(Ty,Py) ~ B(TrsPr)) —a(Te}Iv(Tr, Ps) Guess Psat: Psaty := = Given Ingl(T,,Psat,) = Ingv(T;,Psat;) Paty := Find(Psat;) 3 Psat, = 0.026 — ZI(T;,Psat;) = 4.742 107° Zv(T;,Psat,) = 0.965 Prat = PsatyPe Vebir Ans. The following table lists answers for all parts. Literature values are interpolated from tables in Perry's Chemical Engineers’ Handbook, 6th ed. The last column shows the percent difference between calculated and literature values at 0.85Tc. ‘These range from 0.1 to 27%. For the normal boiling point (Tn), Psat should be 1.013 bar, Tabulated results for Psat do not agree well with this value, Differences range from 3 to > 100%. Ta (Ki) [0.85 Te (K)| Psat (bar) | Psat (bar) [% Difference @Tn @ 0.85 Te[Lit. Values| [Acetylene [ea\~ 160 | et | 2027 | 1878 25% largon a3 {068 | 128s [2023 | 1870 8.2% [Benzene 3532) 160 | 4779 | 16028 | 15.52 32% In-Butane 27a7| 152 | 361s [| 1435 | 12.07 78.9% [Carbon Monoxide | 817 | 092 | 1730 | 162 | 1291 17.7% In-Deca 4473) 2.44 | 6250 | 6633 | 521 27.3% [Ethylene vena} 103 | 2400 [irri | 1769 0.1% In-Heptane 3716] 208 | 4592 | 76o1_| 759 13% [Methane fiat—ort | 1620 | 10.30 | 17.33 11.9% Nitrogen 73) 08s | 1073] 1467} 12.57 16.7% 48514.10 (a) Acetylene: @ = 0.187 Ty = 3083K Po i= 61.39bar Ty 2= 189.4K T:=T, Note: For solution at 0.851, set T:=0.85T,. T; = For SRK EOS: Ty = 0.614 ol e=0 2 = 0.08664 = 0.42748 Table 3.1 ayP ( 2) 2 (Tro) =| 1+ 40.480 + 1.5740 ~ 0.17601 - Ty Table 3.1 a(To}R Te a(t) = ¥— Ba. (8.42) c : T..0) a(T,) = (" ) Fq. 351) B(T;,Pr) Eq, (3.50) Define Z for the vapor (Zv) Guess: Given Eq. (3.49) w= 1+ (TesPs)4()-B(TesP) ae Zv(Ty, Py) == Find(zv) Define Z for the li Given Eq. (3.53) id (ZI) Guess: z1:= 0.01 21> B(T;,Pr) + (21 +e-B(Ty, Py) (zl +0: otra ayy reer -2) att} B(TeP) ‘To find liquid root, restrict search for zI to values less than 0.2, zi < 0.2 Zi(T,,Pr) = Find(zl) 486Define I for liquid (M1) and vapor (Iv) icon (ate) +0-B(Tr,Py) © (ZT,P,)+e-B(TPr) 1 uf 2v(Tr,Pr) ce o~6 | 2o(T;,P:) +6-B(TrPr) Eq. (6.62b) Ingl(T,Pr) = ZI(Te.Pr) 1 = In(Z4(Te,Py) ~ B(Te,Ps)) — a(Ts)-U(Tr, Pr) Eq. (11.36) Inbv(Ty,P,) := Zv(Te,Pp) — 1 - In(Zv(Ty,P:) ~ B(Tr.P)) - a(Tr)Av(T,Ps) Guess Psat: Psat, = 222 Given Ingl(T,,Psat,) = ingv(Ty,Psat;) Psat; := Find(Psat,) Psat; = 0.017 ZI(Ty,Psat,) = 3.108% 10> Zv(T,,Psat,) = 0.975 Poot = PoatyPe —-Pyat = 1.073 bar Ans. The following table lists answers for all parts. Literature values are interpolated from tables in Perry's Chemical Engineers' Handbook, 6th ed. The last column shows the percent difference between calculated and literature values at 0.85Tc, ‘These range from less than 0.1 to 2.5%. For the normal boiling point (Tn), Psat should be 1.013 bar. Tabulated results for Psat agree well with this value. ferences range from near 0) to 6%. [in (K)] Psat (bar)| 0.86 Te (K)] Peat (bar) | Psat (bar) |% Difference ~@tn @ 0.85 Te] Lit. Values: [Acetylene Tea] 1073 | 26a | 20016 | 1378 2% [Argon 673 | 0976 | 1283 | 1878 | 1670 0.5% [Benzene 3532| 1.007 | 4779 | 18658 _| 15.52 0.5%. in-Butane 2727| 1008_| 3613] 12238 | 1207 1.4% (Carbon Monoxide [817 | 1019 | 1130 | 12e71_| 1291 0.3% in-Decane mars} 1014 | 6950 | 5394] 5.21 2.1% {Ethylene ea4] 004 | 2400 | 479i6_| 17.68 13%, In-Hoptane 3716{ 1011 | 4592 [7.779 | 7.59 2.5% [Methane Talos | 1620 | 1746 [17.33 08% Nitrogen 773} 0e2 | 1073 | 12617 [1257 0.3% 48714.10 (b) Acetylene: @ := 0.187 Ty = 308.3K Py :=61.39bar Ty T:=Ty Note: For solution at 0.85T,, set T= 0.85T,. Ty = For PREOS: Tr = 0614 or 1492 e:= 1-J2 Q = 007779 Y = 0.48724 Table 3.1 1 t @(T;,0) a +-(037464 + 1.542260 - aooont hl -12)| eee a} er? a(T,) = (Tre) RTS Eq. 3.42) " w-a(Tr.0) QP, aft, = tee) F951) p(T;,P,) =! Bq. B50) OT, Define Z for the vapor (Zv) Guess: w= 0.9 Given Eq. (3.49) z- B(TrsPy) zv = 1 +B(TesPy) - 9(Tx)-B(Tr.Py) re (t,,P)- (ert on) Zv(Tr Py) = Find(zv) Define Z for the liquid (ZI) Guess: zi:= 0.01 Given Eq. 3.53) 21> B(T,.Pr) + (21+6-8(Tr,P,)) (21+ 0 otraayy( eter) 2) To find liquid root, restrict search for 2 to values less than 0.2 21 < 0.2 ZI(TesPz) == Find(zl) 488Define I for liquid (11) and vapor (Iv) 1 of ergot) ZT,.Pr) + ©-B(T,.P,) U(Tr.Pr) o € Eq. (6.62) Iv(Te.Py) o-e 1 ; w(t TpP,) +6 — Ingl(T,,Pe) == ZI(T,,P,) - 1 ~ In(Zi(T;,P,) — B(Te.Py)) — a(Ts) (Tr. Pr) Eq. (11.36) inov(Ts,Py) := Zv(Te.Pe) — 1 - In(Zv(Te,Ps) ~ B(Te.Pe)) ~ a(Te}Iv(TesPr) Guess Psat: Psat; ae Given ingi(T, ,Psat,) = Inov(T, sats) Psat, = Find(Psat,) Psat, = 0.018 ZA(Te, Psat) = 2.795 x 10) Zv(T; ,Psate) = 0.974 Poot = Prato Phay = 109har Ans. ‘The following table lists answers for all parts. Literature values are interpolated from tables in Perry's Chemical Engineers’ Handbook, 6th ed. The last columa. shows the percent difference between calculated and literature values at 0.85Te. These range from less than 0.1 to 1.2%. For the normal boiling point (Tn), Psat should be 1.013 bar. Tabulated results for Psat agree well with this value. Differences range from near 0 to 7.6%. ‘Tn (K)[ Peat (bay [0.88 Te (K)] Peat (bar) | Peat (bar) | % Difference) @™m ‘@ 0.85 Te| Lit. Values (Acotylene Teaa| 1090 [2627 | teres [1978 [01% ‘Argon 73 {1015 | 1283 | 18676 | 1870 | 0.1% [Benzene 3532] tote | a7r9_| 15.457_|_15.52 “04% in-Butane 2727] 1.016 | 3613 | 12084 | 12.07 0.1% [Carbon Monoxide | 817 | 1.041 | 1130_|tz76a_[_ 1201 “2% In-Decane aars 7.016 | 250 | 6260 [6.21 05%. [Ethylene 768.4] 1.028 [2400 _| tv 7aa_|_ 17.89 0.3% in-Hoptane arte] tote 4592 [767i 7.58 11% Methane Tia] 099 162047342 | 17.33 0.1% [Nitrogen 73 {1016 | 1073 | 12817 | 1257 | _-0.4% 48914.12 (a) van der Waals Eqn. Tr:= 0.7 o=0 s0 apie pees (Tr) = 1 “8 oe walt Pi ate = 209 acre,py = SPE zw := 0.9 (guess) OTe Tr (Tr, Ps Given = zv = 1+ B(Tr,Pr) — 4(T0)-p(Te, Py PEP Eq. 3.49) (wy Zv(Tr,Pr) = Find(zv) zi=.01 (guess) 2 1+ BT, Pr) = zl a(t) BCT, PH) Given 21 = B(Tr,Pr) + (2) Eq. G53) zl< 0.2 Zi(Tr,Pr) += Find(2t) BcTr, Pr) Hictr,P8 = B(Tr,Pr) Zo(Tr, Pr) Z(Tr,PD) By Eq, (11.36): Ingv(Tr, Pr) = Zv(Tr,Pr) — 1 ~ In(Zv(Te, Pr) ~ (Tr, Pe) ~ q(Tr)-Lv(Tr,PY) I(T, Pr) = Bottom pg. 214 Ingl(Tr,Pr) == Zi(Tr,Pr) ~ 1 — In(Zi(Tr, Pr) — B(Tr,Pr)) = q(Tr)-1i(Tr, Pr) Psate := 1 Given Indl Tr,Psatr) ~ Ingv(Tr, Psatr) = 0 Psatr := Find(Psatr) ‘ZW(Tr,Psatr) = 0.839 Zi(Tr,Psatt) = 0.05 Psatr = 0.2 Infl(Tr,Psatr) = -0.148 Ingv(Tr,Psatr) = -0.148 B(Tr,Psatr) = 0.036 = log(Psatr) 302° Ans. (b) Redlich/Kwong Eqn Tr := 0.7 o=l e=0 Q = 0.08664 W := 0.42748 a(t) = Tr * Pah ST) gcresey = SF Guess: OTe Tr a(t 490zv— B(Tr,Pr) z-(zv + B(Tr,Pt)) Given zy = 1 + B(Tr,Pr) ~ 4(T:)-B(Tr, Pr) Eq. (3.49) Zv(Tr,Pr) := Find(zv) Guess: zl:= 0 Given z= B(Tr,Pr) + 2h(z1+ B(Tr,Pp)- 2< 02 Zi(Tr,Pr) = Find(2l) 7 i( 2vCTe,Pe) + BCT PD) ree = \ Zv(Tr,Pr) Iv(Tr,Pr) == Z\(Tr, Pr) By Eq. (11.36): Ingv(Tr,Pr) s= Zv(Tr,Pr) — 1 - In(Zv(Tr, Pr) ~ B(Er, Pd) — q(Tr)-Iv(Tr, Pr) Ingl(Tr,Pr) := ZMTr,Pr) — 1 - in(Zi(Tr, Px) — B(Tr,Pr)) — q(TH)-IMTr, Pr) Psatr = 1 Given _Ingi(Tr,Psatr) = Indy(Tr,Psatr) Psatr := Find(Psatr) Zv(Tr,Psatr) = 0.913 ZI(Tr,Psatr) = 0.015 Psatr = 0.087 Inv(Tr,Psatr) = 0.083 Ingl(Tr,Psatr) = ~0.083 B(Tr, Psatr) = 0.011 = -1-log(Psatr) @ £0,058 Ans. 1415 (@) xlai=01 9 da=t-xla—xIP0.9 2B 1-xIB oaaie Ais 2 Ag =2 la A21.A12) exp| x20? Ar2-+2-(Ani ~ Az} xia] YAB(Agn Ata) = exp] x26°{ Aig +2(Ani - A2)x18] | ya Aor Ay2) = exp] xter{ Ag) +2-(Ar2 ~ Ani) x2e |] 28(Ag1.Ar2) = exp] x18 {Aa +2-(Ar2— Ai) 328 || 431Given xlavylar(Aaq,Ai2) = x1B-718(Aot.Ar2) x2owy2ee(Agi ,A12) = x28-72B(Agy .A12) far) = Find(A12,A2 Agy= 2-747. Aj2= 2.747 Ans. Aa) (b) xla = 0.2 Wast-xla xIB:=09 x2B:= 1-xIp aces Ai2=2 An =2 yle{Aay Ata) = exp] x20 Ara +2-(Aa1 ~ Ara}xlee | 11B(Aa1.Ata) = exp] x26 [Aig +24Aa1 ~ Ara}x1p))] 2a(Agy tz) = exp| xta?[ Agi +2(Ar2 ~ Ani)20] | 28 (Aot Ara) = exo] x16 Ani +24A12—An)}926)] Given xlaryler(Azy,Ai2) = x1B-y71B(Az1 Az) x2a-y2a:(Agq,A12) = x2B-72B(Ap1 ,A12) Ajys 2.148) Ag, = 2.781. Ans. en © xla:= 0.1 Rac I-xla — xIB=08 = x2Bs= 1-x1B Guess: Az = 2 Agi =2 yla(Agi Aya) = exp[ x20? Ato + 2(Ao1 -An)xta]] ‘AB(Aa1.Ar2) = exp] 326°[ Ara +2-(A21 ~ Ayz} xi] ‘a(Aay 412) = exp] xto( Any +2-(Ar2~ Api)}20] | Tor ¥2B(A21 Ara) = exp| xIB"{ Agr +2-(Aj -An)29]]} 492Given xloryla(Agi Ai2) = x1B-y1B(Ag1,Ai2) x2a-y2a.(Az1 Ata) = x2-y2B(Az1,A12) 14.16 (a) xla:= 0.1 Guess: Given ae fi ayyxlay? , if exp) arz| 1+ xloc® exp. a aia a 7 / 2 2! ag x20, 21x28 exp| apy | 142] x20 = exp) azi-| + x28 aj2-xla, ay7-xIB az ae : ( ) := Find(ay2,a21) aj = 2.747 aor Ans. \aa1 f Given apata)?} ( apxip? exp] ay2] 1+ xlot ® exp) aja b+ = x1 B (0 agnx2a., \ aarx2B, ap 1-x2e) exp| arr 1+ ("") = Find(a12,a91) a2xip Given ee exp) aig} 1+——— | xia = L 2 2 a12°x1B) 2} 1 1 of ran fos aa)? agrx28) > \ " aipxia) axip) a2) ind(a12,a21) aj = 281 ag, = 2199 Ans. agi ) 14.18 (a) a= 975 T = 250.450 A(T) 24 T 7 T Parameter A = 2 at two temperatures. The lower one is an UCST, because A decreases to 2 as T increases. The higher one is a LCST, because A decreases to 2 as T decreases. Guess x= 0.25 Given A(T)-(L= 2.) = (=) Eq.) Ex. 14.5 x20 xs05 xI(1) = Find(x) x21) = 1=x1(1) 494UCST = 300 (guess) Given A(UCST) = 2 UCST := Find(UCST) LesT Given A(LCST) 00 (guess) LCST := Find(LCST) Plot phase diagram as a function of T nM 225.1. UCST 500 T T i r T Tl 40F 4 wi 2 300F 4 an \ 1 1 \ 1. 0203. 04 05 06 07 08 AU(TH) x2(T1) ,x1(72) 22(12) (b) a:= 540 bis-I7.1 T := 250.450 A(T) L 250300350 400450 T 495Parameter A =2 at a single temperature. It is a LCST, because A decreases to 2.as T decreases. Guess: x = 0.25 Given A(T)-(1-2-x) & In| Eq. (), Ex. 14.5 x20 x05 x1(T) := Find(x) LCST := 350 (guess) Given A(LCST)= 2 LCST = Find(LCST) LEST. 3.346") Plot phase diagram asa function of TT := LCST. 450 450 400 ale m= 350 F — ieee sce epien seperate ee 397 02 03 04 OF 06 07 08 xi(1), 1x1) © 500 =19.9 T = 250..450 A(T) = (T) TParameter A =2 at a single temperature. It is an UCST, because A decreases to 2 as T increases. Guess: x = 0.25 Given A(T)-(1-2-x) = uf! =] Eq. (E), Ex. 14.5, x x20 x505 — xI(T): Find(x) UCST := 350 (guess) Given A(UCST)= 2 UCST == Find(UCST) Plot phase diagram asa function of TT := UCST..250 350 = 300 T a o 02 04 06 08 1 X(T), 1x) 14.20 Guess: xla: 5 IB = 05 Given Write Eq. (14.70) for species 1: xlovexp| 0.4(1 - xla)?] = xtf-expL o.8-(1 - x18) | xla_ | _xIB Ixia 1-xIp el (Material balance) ind(xla.,x1B) xia 20.371 x18 ='0.291 Ans. 49714.22 Temperatures in kelvins; pressures in kPa. 5363.7 Pisat(T) == ox 9.1478- =) water P := 1600 P2sat(T) s= cn 14651 1- a =!) SF6 1d 3-phase eq) 574-5 of text): rium temperature and vapor-phase composition (pp. Guess: T = 300 Given P= Plsat(T)+P2sat(T) —Tstar := Find(T) star = 281.68 Plsat(Tstar) ylstar ylstar-10° = 695 P Find saturation temperatures of pure species 2: Guess: T := 300 Given P2sat(T) = P 12 = Find(T) TIL := Tstar,Tstar + 0.0001... 12 yII(T) <= 1 - THe Totar, Vstar + 0.01 . Tstar +6 yitcry = PCD P Because of the very large difference in scales appropriate to regions I and II [Fig. 14.20(a)], the txy diagram is presented on the following page in two parts, showing regions I and II separately. yutcrny-10® yimcrap: 108 4981 Tstar 50 700 750~800 850 ~—900 9501000 1050 yliTny- 108, yt1¢r9- 108 14.24 Temperatures in deg. C; pressures in kPa Plsat(T) = exp 14.0098 - pee Toluene \ T+219.79 ee P:= 101.33, P2sat(T) = oa( 16 2620 - =~ Water T+ 226.35, Find the three-phase equilibrium T and y: Guess: T:=25 Given P-= Plsat(1) +P2sat(T)Tstar ind(T) Tstar = 84.333 sat(Tst vylstar := one yistar = 0.444 For z1 y1*, first liquid is pure species 1. 49914.25 yl=0.7 Guess: Tdew := Tstar Pisat(Tdew) gow := Find(Tdew) Tdew = 98.53 Ans. Given yl In both cases the bubblepoint temperature is T*, and the mole fraction of the last vapor is y1*, ‘Temperatures in deg. C; pressures in kPa. Plsat(T) := oo 13.8887 723) a 101.33 P2sat(‘T) + oon{to2ma0- 228) water T+ 226.35 Find the three-phase equilibrium T and y: Guess: = 50 Given P= Pisat(T)+P2sat(T) Tstar := Find(T) star = 82.91 Pisat(Tstar) Istar = 0.474 : y ylstar Since 0.35 Tdew,ylo,yl(T)) T = 100,99.9.. Tstar 500Path of mole fraction heptane in residual vapor as temperature is decreased. No vapor exists below Tstar. 100 95 85 Shs 036 038 04 042 044 046 048 ylpath(T) 14.26 Pressures in kPa. Pisat:=75 Pasa = 110A cat) == exp x1)? lal) := exp(A-x1?) Find the solubility limits: Guess: xla:= 0.1 Given (1-281) w =u) xla:= Find(xta) xla xla = 0.224 xIB —xlo. xB = 0.776 Find the conditions for VLLE: Guess: Pstar := Psat ylstar := 0.5 Given Pstar = x1B-y1(x1B)-Plsat + (1 — xlo)-y2(xla)-P2sat yistar-Pstar = xlo-y1(xIa)-Plsat Pstar | = Find(Pstar,ylstar) star = 160,699 ylstar = 0.405 ylstar ) 601Calculate VLE in two-phase region. Modified Raoult’s law; vapor an ideal gas. Guess: x1 0.1 P= 50 Given P= xi-yl(x1)-Plsat + (1 —x1)-y2(x1)-P2sat P(xl) == Find(P) loa) := XETLGD. Psat Pol) Plot the phase diagram. Define liquid equilibrium line: PL(x}) == if(P(x1) < Pstar, P(x), Pstar) Define vapor equilibrium line: PV(x1) := if(P(X1) < Pstar,P(X1) ,Pstar) Define pressures for liquid phases above Pstar: Pliq := Pstar.. Pstar + 10 x1 = 0,0.01..1 200 ns PLE 50 PV(x1), Pig Pliq 100 5 50 0 02 04 06 08 1 xl yIGrl) xla, x18 80214.27 x1 := 0,0.05..0.2 at BES PLOd) iG" 2 Ofers. eA Fe enol foos} P4956) O24 OF 147.658 G3t4 O48: 165525. 0368) ee 158.508 0387 x1 := 1,0.95..0.8 ee: PLO) yfQ) i Te). eal 085 T3656 ‘063 23] 137.098 0808] oa5). 760907). aaa] os) 156505 oat xia=0224 x1 = 0.776 ylstar =-0.405 Temperatures in deg. C; pressures in kPa. 3799.89 ‘Water: Pi: I HRP ee rea a) on( T+ 20 477.07) n-Pentane: sat(T) := exp| 13.8183 - 247707 T+233.21 ( 2991.32 n-Heptane: —P3sat(T) := exp] 13.8587 — pe) \ T + 216.64, 30 23 1-21-22 Ps (a) Calculate dew point T and liq assuming the hydrocarbon lay 0133 zl 045 100 Qa Ba 1 ~ Xo Guess: Tdewl = 503Given P= x2a-P2sat(Tdewl) + x3a-P3sat(Tdewl) 23-P = x3a-P3sat(Tdew!) Ra+x3a0 5 | Ga, Find(x2a,x3a,Tdew!) Calculate dew point temperature assuming the water layer forms first: xIB Given _x1B-Plsat(Tdew2) = z1-P Tdew2 := Find(Tdew2) Guess: Tdew2 := 100 Tew. 79.055 Since Tdew2 > Tdew1, the water layer forms first (b) Calculate the temperature at which the second layer forms: Guess: Tdew3 = 100 a= 22 x3o. = x20 ylieal ylis2d pao Given P = Pisat(Tdew3) + x2u-P2sat(Tdew3) + x3a-P3sat(Tdew3) yL-P = Plsat(Tdew3) 5 2 yl+y2+y3=1 y2:P = x2a-P2sat(Tdew3) x2a+ x30 = 1 yl y2 y3 ae ‘= Find(y1 ,y2,y3, Tdew3 ,x20.,x301) x2a xB,14.28 yh s0348 ‘Tdew3 = 72.886 (©) Calculate the bubble point given the total molar composition of the two phases ‘Toubble := Tdew3 xa —2 Ba 2 R+23 2+3 x2a = 0.545 x30 = 0.455 Given P = Plsat(Tbubble) + x2a:P2sat(Thubble) + x3a-P3sat (Thubble) ‘Toubble := Find(Tbubble) _ Pisat(Thubble) yl As 0,114 y P ¥ x2a-P2sat(Toubble) Sao P x3or-P3sat(‘Thubble) eee a. ae a ‘Temperatures in deg. C; pressures in kPa. Water: Plsat(T) := exp| 16.2620 — pee) T+22635 477.07 n-Pentane: P2sat(T) := ea(3 8183 - P25] T + 233.21 2991.32 -Heptane: P3sat(T) := SRA eee | P i= 101.33 20320 OAS Biz L-zl-2 (a) Calculate dew point T and liquid composition assuming the hydrocarbon layer forms first: 505Guess; Tdew! := 70 22a: Given P = x2a-P2sat(Tdew!) + x3a-P3sat(Tdew!) 23-P = x3u-P3sat(Tdewl) Xa+x3a= 1 xa) x3a_ | = Find(x2a,x3a.,Tdew!) Tdew! J Tdewl = T1018: x30 = 0.733. x2q°= 0267 Calculate dew point temperature assuming the water layer forms first: xip Guess: Tdew2 = 70 iven xP sat(Tdew2) = 2i-P ‘Tdew2 := Find(Tdew2) ‘Tdew2 = 70.91 Since Tdew1>Tdew2, a hydrocarbon layer forms first (b) Calculate the temperature at which the second layer forms: Guess: Tdew3 x3a xa yli=zl yen Given P = Plsat(Tdew3) + x2a-P2sat(Tdew3) + x30-P3sat(Tdew3) y2_ 2 yL-P = Plsat(Tdew3) yl+y2+y3= 1 3 2B y2-P = x2a-P2sat(Tdew3) X2a+x30= 1 Find(yl ,y2,y3,Tdew3,x2a,,x30) 506yi = 0292 y= 069 ysS 0.339. ‘Tdew3 = 68/793" x2 = 0.1738. (c) Calculate the bubble point given the total molar composition of the two phases ‘Thubble := Tdew3 a= —2 a= 3 +B 2B x2at = 0.662 xa = 0.338 Given p= Plsat(Toubble) + x2c-P2sat(Thubble) + x3ce-P3sat(Tbubble) ‘Tbubble := Find{Tbubble) ‘Toubble = 44.361 Plsat(Tbubble) P x2a-P2sat(Tbubble) P x3o-P3sat(Tbubble) 0872 y3 = 0.037 0. 302) Tea ( 84 0.224) ~ (304.2 P:= 10,20..300 (bar) 3 ‘40.51 73.83, 83.14 (bar em*3/mol K) 1432 © ny 7 Te TH33I5 (KW) 1 Use SRK EOS From Table 3.1, p. 99 of text: c= 0 = 008664 Y= 042748 Gasipsaneniinec satura carrey : 2 14+ (0.480+1.5740~0.1760°)(1— 14") | 507— O-R-Te (14.34) b Pe (14.35) (6.842 10 133.076) a= os 10) 29.679 _ b2P (14.32) aeartraagiae Bat) = = ae 80 z= 1 (guess) Given i 22 ~ Ba(P) BEBO PPO ata Zo(P) == Find(z2) 22(P) + Ba(P) 1n(P) = In] ——————_| (6.62) - ( Za) Z For simplicity, let 0, represent the infinite-dilution value of the fugacity coefficient of species 1 in solution. Eq. (14.99): lia = 0.088 by qj 9 y(P) == exp] | | -(Za(P) ~ 1) ~In(Za(P) ~ Ba(P))} | auee rea ~ a) (2-2 | Psat) == 0.0102 (bar) Vj = 124.5 (em3/mol) Eqs. (14.94) and (14.95), with gsatl=1 and (P-Psatl) =P, combine to git fe Psaty ( v1) wih) = exp] Poy (P) RT) 08ou oor Vi yi(P) A rao? FX 110 a 0 sd 100 150 200 250° 300 P (es) 126.2, as T Te 0.302 14.33 @ = 0.038 10,20..300 (bar) 40.51 34.00, R = 83.14 (bar em?/mol K) 308.15 (K) 0 Trs= Use SRK EOS From Table 3.1, p. 99 of text: ol c= 0 Q = 0.08664 W = 0.42748 a [1 +-(0.480 4 1574-0 —0.17602).(1 — 2° sf > ORTe __ Weak : 14,34) b (14.35) Pe se Pe (7.298% 10 133.076 as) b \6.713 10 26.737 509= (1432) = (14.36) m= 1 (guess) Given 22 - Ba(P} 22 = 1+ Bo(P) ~ q2-B2(P)- (o=68xP)o+eBP) (14.31) Za(P) := Find(z9) (Z2P) +82) fete (6.62b) 1a) = (6.62b) For simplicity, let © represent the infinite-dilution value of the fugacity coefficient of species 1 in solution. 1y23=0.0 Bq. (14.99): i] by 91(P) == exp, [2 (Z2(P) ~ 1) - In(22() — ne] : Coa Ly 4-2} 2(1- wy(2) em 4 Psaty := 2.910" (bar) Vi z= 125 (em3/mol) Eqs. (14.94) and (14.95), with osatl =1 and (P-Psatl)=P, combine to give: ( vy we oat PV, 1) + ool ser Pop (P) 51030 100~«1S0~=«0D~~S=O«S0S«0D Note: y axis is log scale. stChapter 15 - Section A - Mathcad Solutions Final state: lee at 32 degF. BIU BIU (0.02 — cee eae ibptankine (70+ 459.67)-rankine @ Cooling water @70(F)) Cond. 8 € w s 4) comp: Throttle A D ice @ 32) | "| Water @ 70(F) <2 e2O jg Water @ 70 Point A: sat. vapor at 32 degF. Point C: sat. liquid at 70 deg. P 35.79(psia). Point D: Mix of sat. liq. & sat. vapor at 32 degF with the enthalpy of Point C. Point B: Superheated vapor at 85.79(psia) and the entropy of Point A. Data for Points A, C, & D from Table 9.1. Data for Point B from Fig. G.2. 512Wiaeal := Hz ~ Hi - To-(82~ $i) BIU Wideal = 12.466. we Tom Wedotigeat ‘= mdot- Wigeal Wdolideat <13.15kW Ans. (b) For the Carnot heat pump, heat equal to the enthalpy change of the water is extracted from a cold reservoir at 32 degF, with heat rejection to the surroundings at 70 degF. BTU Hy-Hy Qc = “18137 491.67-rankine Ty = Qc: BIU THT x <) Work = 14.018 Woot := mdot Work Waotigeat Wot nee ‘The only irreversibility is the transfer of heat from the water as it cools from 70 to 32. degF to the cold reservoir of the Carnot heat pump at 70 deg. (©) Conventional refrigeration cycle under ideal conditions of operation: Isentropic compression, infinite flow rate of cooling water, & minimum temp. difference for heat transfer = For sat, liquid and vapor at 32 degF, by interpolation in the table: BTU BTU Ha := 107,60-—— Sa c= 0.2223-———___ - Dm be Ibgrrankine For sat. liquid at 70 degF: TU He := 34.58-——— Hp = He Ic es p= He For superheated vapor at 85.79(psia) and S = 0.2223: BIU ‘Hg = 114—— ' Tom 513rent circulation rate: Ibm (Hp - Hy) : = mdot = 2.484—" mdot Ha-Hp see Wdot := mdot-(Hg ~ Ha) Waot=16.77kW Ans. Wdotigeat 2 nye 0784 Ans. Th Wdot It. The irreversibilities are in the throttling process and in heat transfer in both the condenser and evaporator, where there are finite temperature differences. (4) Practical eyele. Point A: Sat. vapor at 24 degF. Point B: Superheated vapor at 134.75(psia). Point D: Mix of sat. lig. and sat. vapor at 24 degF with H of point C, Point C: Sat. Liquid at 98 degF. (Note that minimum temp. diff. is not at end of condenser, but it is not practical to base design on 8-degF temp. diff. at pinch. See sketch.) 8@) 90) ye id and vapor at 24 degF: For sat, e 514For sat, liquid at 98 degF, P=134.75(psi He = 44.24- BIL S¢ 25 0.0902-—BIU_ mm ar Fankine For isentropic compression, the entropy of Point B is 0.2229 at P=134.75(psia). From Fig. G.2, Hp-H, Hye 1 i" BTU The entropy at this His He So aneeib read from Fig. G.2 at P=134.75(psia) Hp- Hi 0228 BY yee xp eo up = 0.288 Tbgyrankine Heap ~ Fig BTU Sp = Stiq + ¥D-(Svap ~ Sti Sp = 0.094 1D = Siiq + xD-(Syap ~ Stig) D Roe Refrigerent circulation rate: Ibm -(Hp-Hy).1-28 mdot := ————_S° ndot = 2.91428 ecceeHAe Ap) see Webot := mdot-(Hp ~ Ha) Waot AT22KW Ans. Wdotigeal Wdot eH nig = 0.979" Ans. THERMODYNAMIC ANALYSIS Tg: (70+ 459.67)-rankine Wadotjost.compressor *= mdot-Ty+(Sp- S4) Qdoteondenser ‘= mdot-(Hc - Hp) Weottost.condenser °= mdot-Tg-(Sc ~ Sg) ~ Qdotcondenser 515Waotjostthrottle = mdot’Tg-(Sp - Sc) Weotjostevaporator °= To-/ mdot(S4— Sp) .. 1 bm +L—(S2-s)) L sec J Welotigcay = 13.152kW 27.85% Weotiost compressor = #.305kW 17.59% ‘Wadotjostcondenser = 14A78KW 30.02% Waitiost:throttle = 6.621 kW 14.02% Weloticstevaporaior = 4.968kW. 10.52% The percent values above express each quantity as a percentage of the actual work, to which the quantities sum. 51615.2. Assume ideal gases. Data from Table C.4 282984. AGg9g := 2571903 Allo AH298 ~ AGo9g as 298 398.1 5K J ASo9g = ~86.513 1298 K BASIS: 1 mol CO and 1/2 mol 02 entering with accompanying N2=(1/2)(79/21)=1.881 mol nico = Iemol — Myip = 2.381-mol —ngoy == I-mol nz = 1.88]-mol (a) Isothermal process at 298.15 K: 2.38 air 2.88 ar 5! Since the enthalpy change of mixing for ideal gases is zero, the overall enthalpy change for the process is AH := AHy9g For unmixing the air, define aN? n= N=079 yp By Eq. (12.35) with no minus sign: Sunmixing = Pair R-(yr-In(y1) +y2-In( AS, i ruining = ~2017 5t7For mixing the products of reaction, define 02 BN2 + ACO? y= 0347 2 neo2 + AN2}-R-(yr-ln(y1) + yo-In(y2)) ASmnixing = 15. 465. — AStnixing “= AS °= ASunmixing + AS298 + AS icing -81 m3 300-K Wideal ‘= AH - Tg-AS Ans, Te (b) Adiabatic combustion: 1 mol CO, 1.88 mol N sie 298.15 K 1 mol CO AFapx 0.5 mol O» 1.88 moi No Heat-capacity data for the product gases from Table C.1: n02'5:457 + nyz'3.280 coe A= 11.627 mol nco2' 1.045 + my2-0.593. 5 oo B= 216x109 mol ncog'— 1.157 + nyz-0.040 eee 0° D = -1.082% 10° mol 5181 C1 For the products, AHp® «| = ar To = 298.15-K To ‘The integral is given by Eq, (4.7). Moreover, by an energy balance, AHy9g + AHp = 0 Guess < Given For the cooling process from this temperature to the final temperature of 298.15 K, the entropy change is calculated by 10P3(2622.6, 298.15, 11.627,2.160-10"$,0.0,~1.082-10°) = -29.701 ICPS := -29.701 AS := R-molb ICPS AS = ~246.934 2 Wideal.cooling = AH - Tg-AS AH = -2.83 x 10°) Wigeai séoiing = ~2089043 Ans. Wideal.coolins ny = ne ne= 0.8078 Ans. Wideat ‘The surroundings increase in entropy in the amount: Qo (AH298- Wideatcooting) —ASg == x wee The irreversibility is in the combustion reaction. Ans. 51915.3 1 Saturated vanor 2.700 kPa H,= 26017 BOK OF te f swam, / vival Saturated Squid S,= 8.2244 ‘TRICKS | 1.000 kPa oa 479.88 C; 45303 K 2_ Saturated vapor 275 kPa Hy» 27207 S,= 7.0201 For the sat, steam at 2700 kPa, Table F.2: ks KI Hy = 2801.7 Sp = 62244 1 z 7 ek For the sat. steam at 275 kPa, Table F.2: ky kJ H == 2720.7-- Sa := 7.0201-—— 2 ie 2 kek For sat. liquid and vapor at 1000 kPa, Table kJ ki ‘jig *= 762.6-— Shi 2.1382-—— Hig kg Ha kek KI kJ Hyg; nd Syap *= 6.5828 —— Trot *= 453.03K p= 262 =p ek 7 (a) Assume no heat losses, no shaft work, and negligible changes in kit and potential energy. Then by Eqs. (2.30) and (5.22) for a completely reversible process: ic Ag(H-mdot) = 0 Ag(Semdot) = 0 We can also write a material balance, a quantity requirement, and relation between H3 and S3 which assumes wet steam at point 3. ‘The five equations (in 5 unknowns) are as follows: Guesses: mdoty = 0.1-88 ——mdoty s= mdotymdoty += mdoty + mdoty s Hy +H) H3— Hig $3 = Sgt —— 2 ecetnaceaer ee H3 520Given Ki Hy-mdots — Hy-mdot) ~ Hy-mdot = 0 8 lots ~ Sy-mdoty ~ Sp-mdot = 0 sK ki mdots = mdoty + mdoty (H3 ~ Hijg)-mdots = 300 Hg ~ Hii 83 * Stiq + _ sat mdot; mdoty mdots | := Find(mdot , mdotz,mdot,H3,83) Hs 83 ‘mdots poor Hy= 27679 Ee Re Steam at Point 3 is indeed wet. (b) Turbine: Constant-S expansion of steam from Point 1 to 1000 kPa results in wet steam of quality : S1-Stig tHe . Xb = Sig Hiturb = Hig + Xturo-(Hyap — Hig) 3 ky Xturb = 0.919 Hiusp = 2614107 Neurb *= 0.78 Hrs = Hy + Meurb-(Hturb~ Hi) Hyyrb = 2.655 x 10° kg 921quip = Sturb == Stig + Xturb (Svap~ Sig) Ky turd = 0.94 Sub = 65167 Compressor: Constant-S compression of steam from Point 2 to 1000 kPa results in superheated steam. Interpolation in Table F.2 yields Heomp ?= 2993, se Neomp ?= 0.75 ( Hreomp ~ Ha KI Heomp ‘= Ha ema Hoomp = soe Jeomp ; Pa By interpolation: Scomp *= 7.1803: kK ‘The energy balance, mass balance, and quantity requirement equations of Part (a) are still valid. In addition, The work output of the turbine equals the work input of the compressor. Thus we have 4 equations (in 4 unknowns): Guesses: mdot, == 0.086 8 dot := 0.064 88 s s mdots := 0.1588 Hy := 2770.82 5 kg Given (Heomp ~ Ha)-mdoty = -(Htars — Hs)-mdoty Hy-mdot3 — H-mdoty ~ Hy-mdotg = 082 $ any KI mdots = mdot) + mdot (H5 - Huig):mdots = 300 5 mdoty mdot = Find(mdoty .mdot2,mdot3, H3) mot Hs } 522Steam at Point 3 is slightly superheated. ki By interpolation, 83 65876 Fe THERMODYNAMIC ANALYSIS — Tg := 300K _—_ (assumed) By Eq. (5.25), with the enthalpy term equal to zero: Wdotigeal ‘= To:(mdots-$3 ~ mdoty-$1 — mdotz-S2) Wdotigeat = 6.014kW Waottostturb := Tormdoty-(Sturo~ Si) Wotiost.comp := Te'mdot- (Scomp ~ S2) Weotost.mixing To-| (mdots-$3 ~ mdoty-Sturb) ~ mdotz-Scomp | 48.2815% 34.1565% 17.5620% The percent values above express each quantity as a percentage of the absolute value of the ideal work, to which the quantities sum. 623Some property values with reference to Fig, 9.1 are given in Example 9.1. Others come from Table 9.1 or Fig. G.2. For sat. liquid and vapor at the evaporator temperature of 0 degF: BTU Hig = 12.0905" Hyap = 103,015 222. BTU BTU 8, = 0.22525-———__—_—— Stig := 0.02744 ——___ tied Ibarrankine : Tbrankine For sat. liquid at the condenser outlet temperature of 80 deg: Hy = Hq Hi - Hii xs $1 = Stiq + x1-(Svap - Stiq) yap — Hig : BTU x1 = 0.285 eles Tope tankine From Example 9.1(b) for the compression step: Hg := Hy + AH Hy = 120.5220 Ibm From Fig, 9.3 at H3 and P = 101.37(psia): i BU 83 = 0.231 ine aot t= 1845.15 7 if Weot := mdot-AH Waot = 3.225 ot F 524‘The purpose of the condenser is to transfer heat to the surroundings. Thus the heat transferred in the condenser is Q in the sense of Chapter 15; ie.,it is heat transfer to the SURROUNDINGS, taken here to be at a temperature of 70 degF. Internal heat transfer (within the system) is not Q. The heat transferred in the evaporator comes from a space maintained at 10 degP, which is part of the system, and is treated as an internal heat reservoir. ‘The ideal work of the process is that of a Carnot engine operating between the temperature of the refrigerated space and the temperature of the surroundings. To = (70+ 459.67)-rankine TH=To Qdote : 120000 272 Tes (10 + 459.67)-rankine uote 4 BTU Weotigea) = |Qdot Weotideal = 1.533 x 10° —— ideal = |Qdotc| s tideal = Wotjost comp *= Tormdot-(S3—S2) Hq — H)-mdot Qdot = -1.523 x 2Te Waotios.cond = Te-mdot-(S4— $3) — Qdot Wdotiost throttle “= Temdot-(S - Sa) Wedotjost evap = Te-mdot (82 - $;) Hy ~ Hp Te +To° -mdot 525The final term accounts for the entropy change of the refrigerated space (an internal heat reservoir). Wot ™15309 jae Webticsisomp. Waotioe cana 3625: 2a BTU 4730.2—— obits Waotlost.trattie 2 Wabotpsccép = 2047 “— 47.53% 17.42% 11.24% 14.67% 9.14% ‘The percent values above express each quantity as a percentage ofthe actual work, to which they sum: Weor = 32282: 3a The discussion at the top of the second page of the solution to the preceding problem applies equally here. In each case, To = (70+ 459.67)-rankine TH = Te ‘The following vectors refer to Parts (a)-(e): (40 459.67)-rankine 526 600 500 Qdote := | 400 | BTL see 300 200 > TH Walotigeat = {loiFor sat. liquid and vapor at the evaporator temperature, Table 9.1: 21.486 107.320 18318 105.907 Hyap 2= | 104.471 Ie 103.015 101.542 0.04715 0.22244 0.04065 0.22325 Stig := | 0.03408 0.22418 aes 0.02744 0.22525 0.02073. 0.22647, For sat. liquid at the condenser temperature: ‘Hyg := 37. on 84 = 0, 0190 Hy = Hy Hi-H pee eee xis ing Hn Stig + xt-(Svap ~ Stig) | From the results of Pb. 9.9, we find: AIT From these values we must find the 118.9 ‘corresponding entropies from Fig. G.2. 0.1 [Bt ‘They are read at the vapor pressure for he 80 degF of 101.37 kPa. The flow rates 121.7 come from Problem 9. 123.4 0207 8.653 0.229 7361 BTU. $315] 0.231 | ——_ mdot := | 6.016 Ibyrtankine 34] ais | 0.237, 3.146, 927ae [To-mdot-(S3 - $2) (Hg - H3)-mdot] —_ [To-mdot-(S4- $3)] ~ Qdot ——___»> [To-mdot-(: - 5, Wdotjost throttle —~——__—_> Webotiosievap = [Te-mdot-(S2 - $;)] gE Nets Hy) - Hp +) [ToS fmdor ‘The final term accounts for the entropy change of the refrigerated space (an internal heat reservoir). 52815.6 In cach case the ideal work and the lost work terms sum to give the actual work, and each term may be expressed as a percentage of the actual work. The discussion at the top of the second page of the solution to Problem 15.4 applies equally here. Tq == (70-4 459.67)-rankine Te = (30+ 459.67)-rankine TH Wadotigegi = 163.375—— Waotieal see (lave re BTU For sat. liquid and vapor af the evaporator temperature, Table 9.1: sais BU by, lbm-rankine 7.978. BEY Ibm From Problem 9.12, = 116-BTU Soa s= 02435.—BTU Hoa Us: Tbarrankine 529\ Hy = Haq + 14,667.51 Hy = 130.67 BTS From Fig. G.2 at this enthalpy and 33.11(psia): BTU byrrankine S3 = 0.2475- Energy balance on heat exchanger: Hy == H4- Hoa +H2 Hy = 27885220 Ibm $1 := Stiq + x1-(Svap — Stig) BIU 8} = 0.061 > Tbgytankine Upstream from the throttle (Point 4) the state is subcooled liquid with the enthalpy: Haga = Hy The entropy at this point is essentially that of sat. liquid with this enthalpy; by interpolation in Table 9.1: 0.059621 _ Tbprrankine Saa ? Ibm, From Problem 9.12: mdot := 25.634-—= sec. Wotios..comp = Tormdot-($3 ~ S24) Qdot := (H4- H3)-mdot Weotjos.cond °= To'mdot-(S4— $3) - Qdot 530Weotiostthrottle = Te-mdot (8; - S4a) Wabotiost.evap ‘= Te-mdot-(S2 - $1) Hp) oo | mdot Te } The final term accounts for the entropy change of the refrigerated space (an internal heat reservoir). Weotjostexchanger *= Ta-mdot-(S2q - So +S4a— $4) Wot := mdot-(H3 - H2a) 3.45% 14.45% 23.16% 11.99% 4.30% ‘The figures on the right are percentages of the actual work, to which the terms sum. 53115.7 0.5 kg/s 2 ¥ i 3 1_ Feed Slury Toe | \ 100 C Compression to a pressure at which condensation in coils occurs at 110 degC. Table F.1 gives this sat. pressure as 143.27 kPa Meomp '= 0.75 Hy 4io.ne (sat, liquid) kg i ki Hy = 2676.0-5 $2 1= 7.3554 (sat. vapor) 2 z 2 eR ah eapo) For isentropic compression (o 143.27 kPa, we find by double interpolation in Table F.2: - Hp 5 := 2737.02 Hy = Hp+ : Hy = 275732 kg Neomp kg By more double interpolation in Table F.2 at 143.27 kPa, $3 = 7.4048 By an energy balance, assuming the slurry passes through unchanged, KI Hag i= Hy + Hy -Ho Hy = 500.45— g 532158 This enthalpy is a bit larger than that of sat, liquid at 110 degC; find quality and then the entropy: a Cy ‘ a 461.3-— Hyy := 2230.0-— Stic 1.4185-—— ke ke ma iek kt Hy — Hig $203-— a = 0018 kek eee 2 S4= Stig + X4°S] Sq = 1.5206 ue mdot == 0.5: 14 Sig’ X4-Stv S84 = 1.520055 = 0 To = 300K Weotideas = mdot{ Hg - Hi ~ To-(S4 ~ $1) ] Weottosrevap = mdat-Te-(S4-$3+S2-S1) Weotiostcomp = mdot-To-(S3 - S2) ‘Wot := mdot-(H3 — Ho) 21.16% 60.62% 18.22% The figures on the right are percentages of the aM actual work, to which the terms sum. ‘Wadot = A thermodynamic analysis requires an exact definition of the overall process considered, and in this ease we must therefore specify the source of the heat transferred to the boiler. Since steam leaves the boiler at 900 degF, the heat source may be considered a heat reservoir at some higher temperature. We assume in the following that this temperature is 950 degF. ‘The assumption of a different temperature would provide a variation in the solution. 533‘The ideal work of the process in this ease is given by a Carnot engine operating hetween this temperature and that of the surroundings, here specified to be 80 degR. We take as a basis 1 bm of H2O passing through the boiler. Required property values come from Pb. 8. Ty '= (459.67 + 950)-rankine Tc := (459.67 +80)-rankine Ta == Te Subscripts below correspond to points on figure of Pb. 8.7. AY) (2576 S1\ (03070 He 1461.2 & 1.6671 1282.2] aru Ss} }i74a31} pru 1047.8 | Ibm sa|* | 1.9748 | Ibperankine Hs 69.7 s5| | 0.1326 Hy} \2502 s;) (oat Widea For purposes of thermodynamic analysis, we consider the following 4 parts of the process: The boiler/heat reservoir combination ‘The turbine ‘The condenser and throttle valve ‘The pump and feedwater heater Te: is Si}t te St] Wiost.boiler.reservoir m := 0.18688:lbm (From Pb. 8.8) ‘o-L m-(S3 - $2) + (I-lbm=m)-(S4 ~ S2) | ‘The purpose of the condenser is to transfer heat to the surroundings, The amount of hea Wiostturbine 1 Ibpy Hs — (-lbm ~ m)-Ha ~ m- Hy -829,045BTU 53415.9 g'[l-lbpr$s — (I-lbm~m)-S4—m-$7}~Q Wiostcond valve Wiostpurap heater “= Tor[,I-lbmr(S1 - Ss) + m-(S7~ $3) ] The absolute value of the actual work comes from Pb. 8.8: Wabsvanue = 374.6FBTU 50.43% 30.24% 13.30% 4.90% 119% 42.82111U ‘The numbers on the right are percentages of the absolute value of the ideal work, to which they (absolute value) sum, Refer to Fi the liquefaction section to the right of the dashed line. Enthalpy and entropy values are those given in Ex. 9.3 plus additional values from the reference cited on page 323 at conditions given in Ex. 9.3. re 9.7, page 322, The analysis presented here is for Property values: ‘Hg := 1140.0- oo kg i Hg := 1009,7-— S: = 83894 kg 7 kek i Ki Hy := 719.8-— 144 a kg kg-K Ho := 285, add 28. kg kek ki Sto 5 9.521 a kek 535Hg = Hs S6:= Ss Hi Hio S12 = Sio To i= 295K The basis for all calculations is 1 kg of methane entering at point 4. All work quantities are in kJ. Results given in Ex. 9.3 on this basis are: Fraction of entering methane that is liquefied: Fraction of entering methane passing through the expander: On this basis also Eq. (5.26) for Ideal Work, Eq. (5.33) for Entropy Generation and Eq. (5.34) for Lost Work can be written: Wiost = Ta SG al = A(H-n)gs Tor (Sem)p, Sq = A(S-m)g,— Wideal = [His:(1 =z) + Ho-z~ Ha] -To[S15-(1 - 2) + S¢-z- $4] Re (b) Heat Exchanger Il: So,p := [ (S7- S6)-(1 - x) + (Sia - Si3)-(1-2) ] S0313A- — Wosth = Te Se. = 92.24 Soo Mea lostb Sab Wiostb eg 536(@) Throttle: Soa'=[Soz+ Syo(1-2-x)-Sr~%)] Wiostd Entropy-generation analysis: SGy SG S_Ge $4 x = TeSad kiMkeg-K 0-044 0.313 0.157 0.964 1478 Work analysis, Eq. (15.3): Note that: kaikg $3.20 92.24 4624 28430 489.00 Es |Wigeall 837 Percent of ¥ 2.98% 21.18% 10.62% 68.22% 100.00% Percent of 10.88% 2.66% 18.86% 9.46% 58.14% 10.00%Chapter 1 - Section B - Non-Numerical Solutions 1.1 This system of units is the English-system equivalent of SI. Thus, Be = (by )()(poundal)~ 1.2 (a) Power is power, electrical included. Thus, energy ‘ime (®) Blectric current is by definition the time rate of wansfer of electrical charge. Thus Power [=] Charge [=] (electric current)(time) [=) A-s (0) Since power is given by the product of current and electric potential, then current As (@) Since (by Ohm’s Law) current is electric potential divided by resistance, werk Electric potential [=] P°** a electric potential current als kgm? Resistance [=] = (6) Since electric potential is electric charge divided by electric capacitance, charge, Ast Capacitance [=] = [=] ‘apacitance ] ieSrie potential gg? 1.3 The following are general: Inx = In10 x logigx Cy 100_ kPa P#/kPa = P™/tom x — z On * Rss wo (PC =T/K~ 273.15 © By Eqs. (B) and (4), 100 In P*/kPa = In 10 logy P™/ es ie B10 PM tor + In 756 Ger The given equation for logiy P* /torr is logy) P*/torr Combining these last two equations with Eq. (C) gives: tno (a7, in Pika, a + ina TK 27 750.061 3 3026 (a~ pe) - \ WK) en ‘Comparing this equation with the given equation for In P™/kPa shows that: A= 2.3026 a — 2.0150 B= 230266 ce =273.15 5391.9 Reasons result from the fact that a spherical container has the minimum surface area for a given interior volume, Therefore: (@ A minimum quantity of metal is required for tank construction. (6) The tensile stress within the tank wall is everywhere uniform, with no sites of stress concentration. Moreover, the maximum stress within the tank wall is kept to a minimum, (©) The surface area that must be insulated against heat transfer by solar radiation is minimized. its of mass-velocity®. Its fundamental units are therefore: 1.17 Kintic energy as given by Eq. (1.5) has u Ex Leg? [=] Nm (JS Potential energy as given by Eq. (1-7) has units of mass-length-acceleration. Its fundamental units are therefore: Ee f)kemms 1.20 See Table A.1, p. 652, of text, ‘© (atm) * 1 bar = 1/0.986923 = 1.01325 bar © (Btu) © 1 kJ = 1/0.947831 = 1.05504 ks © I(hp) = 0.75 kW = 1/1.34102 = 0.745701 KW ‘# 1(in) = 2.5 om = 2.54 om exactly, by definition (see p. 651 of text) # Iifbq) = 0.5 kg = 0.45359237 kg exactly by definition (see p. 651 of text) ‘= l(mile) ~ 1.6 kan = $280/3280.84 = 1.60934 km (quart) © 1 liter = 1000/ (264.172 x 4) = 0.94635 liter (I Titer = 1000 em?) yard) ~ 1m = (0.0254)(36) ~ 0.9144 m exactly, by definition of the (in) ané the (yard) An additional item could be: © Moile)(i)-!~ 0.5 m s“!= (5280 /3,28084) (1/3600) = 0.44704 m st 1.21 One procedure here, which gives results that are internally consistent, though not exact, is to assume: 1 Year [=] 1 Ye [+] 364 Days This makes 1 Year equivalent to exactly 52 7-Day Weeks. Then the average Month contains 30! Days and 4} Weeks. With this understanding, 1 Year [=] 1 Yr [=] 364 Days [=] (364)(24)(3600) = 31,449,600 Seconds Whence, #1 Se [=] 31.4496 Second 1 Second [=] 0.031797 Se 1 Mn [=1314.496 Second 1 Minate [=] 60 Second [=] 0.19078 Mn #1 Hr (=] 3144.96 Second 1 Hour [=] 3600 Second {=] 1.14469 Hr #1 Dy [=]31449.6 Second 1 Day [=] (24)(3600) Second [=} 2.74725 Dy #1 Wk (=1314496, Second 1 Week (=] (7)(24)(3600) Second (=] 1.92308 Wk #1 Mo [=] 3144960 Second 1 Month =} (4)(7)(24)(3600) Second[=] 0.83333 Mo The final item is obviously also the ratio 10/12. 540umerical Solutions Chapter 2 - Section B - Non-! 2.3 Equation (2.2) is here written: AU" + AEp+ AEK=Q4+W (@) In this equation W does not include work done by the force of gravity om the system. This is accounted for by the AEy term. Thus, W’ = 0 (&) Since the elevation of the egg decreases, sign( AE) is (~>) (6) The egg is at rest both in its initial and final states; whence AEx = 0. @ Assuming the egg does not get scrambled, its internal energy does not change; thus AU" = 0. (©) The given equation, with AU" = AE, = BV = 0, shows that sign(Q) is (—). A detailed examination of the process indicates that the kinetic energy of the exg just before it stikes the surface ppears instantly as internal energy of the egg, thus raising its temperature. Heat transfer €0 the surroundings then returns the internal energy of the egg to its inital value 26 If the refrigerator is entirely contained within the kitchen, then the eleciricsl energy entering the re fiigerator must inevitably appear in the kitchen. The only mechanism is by heat transfer (from the condenser of the refrigerator, usually located behind the unit or in its walls). This raises, rather than lowers, the temperature of the kitchen, The only way to make the refrigerator double as an air condi- tioner isto place the condenser of the refrigerator outside the kitchen (outdoors) 2.7 According to the phase rule (Fg, (2.7)], F = 2~ 1 +N. According to the laboratory report a pure ‘material (= 1) isin 4-phase (x = 4) equitibrium. If this is true, then = 2~4 41 = —1. This is not possible; the claim is invalid, 2.8 The phase rule (Eq. (2.7) yields: F =2—x +N =2-2+2=2. Specification of T and P fixes the intensive state, and thus the phase compositions, ofthe system. Since the liquid phase is pure species 1, addition of species 2 to the system increases its amount in the vapor phase. Ifthe composition of the vapor phase is £0 be unchanged, some of species 1 must evaporate from the Liquid phase, thus decreasing the moles of liquid present. 2.9 The phase rule [Eq (2.7)] yields: F = 2— 3 +N =2-243-=3. Withonly 7 ond P fixed, cone degree of freedom remains. Thus changes in the phase compositions are possible for the given T and P, [ethanol is added in a quantity that allows 7 and P to be restored to their initial values, the ethanol distributes itself between the phases so as to form new equilibrium phase compostions and altered amounts of the vapor and liquid phases, Nothing remains the same except 7 and P. 2.10 (a) Since F = 3, fixing T and P leaves a single additional phase-rule variable to be chosen, (©) Adding or removing liguid heving the composition of the liquid phase or adding or removing vapor having the composition of the vapor phase does not change the phase compositions, aid does not alter the intensive state ofthe system, However, such additions or removals do alter the ‘vera composition of the system, except forthe unusual ease Where the two phase compositions aze the same, The overall composition, depending on the relative amounts of the two phases, cat range from the composition of the liquid phase to that ofthe vapor phase. 2.14 Ifthe fuid density is constant, then thc compression becomes a constant-V’ process for which the work is zero. Since the cylinder is insulated, we presume that no heat is transferred, Equation (2.10) then shows that AU = 0 for the compression process. S412.16 Electrical and mechanical irreversibilities cause an increase in the internal energy of the motor, manifested by an elevated temperature of the motor. The temperature of the motor rises until a dynamic equilibrium is established such that heat transfer from the motor to the stroundings exactly compen- sates for the ireversibilites. Insulating the motor does nothing to decrease the irreversbilities in the motor and merely causes the temperature of the motor to rise until heat-transfer equilibrium is reestablished with the surroundings. The motor temperature could rise toa level high enough to cause damage. 2.19 Lot symbols without subscripts refer to the sotid and symbols with subscript w refer to the water. Heeat transfer from the solid to the water is manifested by changes in internal energy. Since energy is. conserved, AU" = — AU, If total heat capacity of the solid is C' (= mC) and total heat capacity of the water is Ci, (= mCu), then: CUT = To ~ChTe = Ton) or Teo ~ Ee(T ~ Ta) 4) equation relates instantaneous values of 7, and 7. Itcan be written in the alternative form: TC! — T9C! = ToC, ~ ToC or Tag, + TC! = Ty, TC! (By ‘The heat-transfer rate from the solid to the water is given as Q = K (Ty — 7). [This equation implies that the solid is the system.] It may also be written: ar 1 = Kha c) OF =Kte-D « In combination with Eq, (4) this becomes: i: «[tm-Go-m-7] where both @ and # are constants. The preceding equation may now be written: aT dt a 1d(a~ AT) Br B a-aT -pr at Rearrangement yields: Integration from Ty to T and from 0 to r gives:aT a Blo which may be written: xp(—Bt) When solved for ' and rearranged, this becomes rage(n- %) exp(-Pr) 3 @ Tah + ToC! whereby the definitions of « and p, = TT When + = 0, the preceding equation reduces to 7 = To, as it should, When r = 00, it reduces to T = a/f. Another form of the equation for af is found when the numerator on the right is replaced by Eq. (B) a _TCh4TC By inspection, T—=a/8 when T=, the expected result. 220 The genoral equation applicable here is Eq. (230): al(i+$ o+W, (a) Write this equation for the single stream flowing within the pipe, neglect potential- and kinetic. energy changes, and set the work term equal to zero. This yields: (Alyn = @ (®) The equation is here writen for the two streams (Land I} lowing in the two pipes, again neglecting ‘any potential- and kinetic-energy changes. There is no work, and the the heat transfer is internal, between the two streams, making Q = 0. Thus, (AM + AM = 0 (©) Fora pump operating on a single liquid stream, the assumption of negligible potential- and kinetic- energy changes is reasonable, as is the assumption of negligible heat transfer to the surroundings. Whenee, (Am = (@) Fora properly designed gas compressor the result is the same as in Part (¢). (©) Fora properly designed turbine the result is the same as in Part (c). () The purpose of a throttle is to reduce the pressure on a flowing stream, One usually assumes adiabatic operation with negligible potential- and kinetic-energy changes. Since there is no work, the equation is: AH=0 (g) The sole purpose of the nozzle is to produce a stream of high velocity. The kinetic-energy change must therefore be taken into account. However, one usually assumes negligible potential-energy ‘change. Then, for a single stream, adiabatic operation, and no work: A[(i + x) m] = 0 The usual case is for a negligible inlet velocity. The equation then reduces to: AH+ lu =o 5432.21 We reformulate the definition of Reynolds number, with mass flowrate m replacing velocity w ty = udp =u =D? p= uD? p Solution for w gives: ‘Whence, Re (@) Clearly, an increase in results in an increase in Re. (6) Clearly, an inetease in D results in a decrease in Re. 2.24 With the tank as control volume, Eqs. (2.25) and (2.29) become: dm dent) pa ang Sent) dt a . dt Expanding the derivative in the second equation, and eliminating ri by the first equation yields: +H Multiply by dr and rearrange: Substitution of #7’ for AT requires the assumption of uniform (though not constant) conditions through ‘out the tank. This requires the absence of any pressure or temperature gradients in the gas in the tank. 2.32 From the given equation: P rs oRT By Fq.(13), [Pav = f por Whence, 2.38 Recall: aPV)=Pdv+¥aP and = dW = Pav Whence, = dW =VdP—a(pv) and [Wa fPdP APY) ByEg.@24), dQ =dU -aw ByEg.Q.10, U=H-PV and dU =dH~Pd¥—VvaP With div =—P dV the preceding equation becomes dQ = dH ~ VdP Whence, [Q=aH-fVaP 54gumerical Solutions Chapter 3 - Section B - Non- 3.2 Differentiate Eg. (3.2) with respect to P and Bq. (3.3) with respect to (Ge), =~95 (5), Ge), +7 (sear) = * ear) (ir), = 7 (Sr), Gs), & Caran) =P ( Addition of these two equations leads immediately to the given equation. x is not covered until Chapter 6. h(i Ei sia) where Vo, A, and B are constants. Application of Eq, (3.3), the definition of x, requires the derivative of tis equation: av A, _4P_]_ an (),-% B+P” (B+PP] B+P “Multiplication by —1/¥ in accord with Eq, (3.3), followed by substitution for Vo/ ¥ by the Tait equation leads to: AB @+ PBFA API 3.7 (a) For constant T, Eq, (3.4) becomes: * = «dP 3.3 The Tait equation is given as: Integration from the initial state (P), V;) to an intermediate state (P, V) for constant « gives ¥ 4 ina etP PD) Whence, V = Moexpl-«(P — A) ‘exp P) expe P,) If the given equation applies to the process, it must be valid for the initial state; then, A(T) = FrexpicPi), and KT) exp(—KP) (0) Differentiate the preceding equation: dV =~ A(T) exp(-«P)dP Therefore, wa_f' par A =KA(r) [ Pexp(-«P)dP de, A(T), AMP + Dexp-eP) = (Pet Despre PJ] 345With ¥) = A) exp(—e Pi) and Vy = A(T) exp(—KeP;),_ this becomes: eae o | 3.11 Differentiate Eq. (3.34e) with respect to 7: 1=8) pra-nara a? 4 pa-aye AT _ (18) PUPA AP pune aT ge ae ers area Algebraic reduction and substitution for d P/dz by the given equation yields: Tie PVG ar as lo ye Mrs) + Foran ideal gas T'p//P = 1/R. This substitution reduces the preceding equation to: 3.12. Example 2.12 shows that U2 =H’ If the gas is ideal, HaU'S PV "RT! and Uy—U"= RT! Forconstant Cy, U;—U" =Cy(Ip- 1’) and Cy(Ty~T") = RT” Whence, When Co/Cy is set equal to y, this reduces to yt This result indicates that the final temperature is independent of the amount of gas admitted to the tank, a result strongly conditioned by the assumption of no heat transfer between gas and tank. 3:13 Isobarie case (5 = 0). Here, Eqs. (3.35) and (3.36) reduce to W =-RT0" = 1) and 2 rahe —1) Both are indeterminate. The easiest resolution is to write Eq, (3.35) and (3.36) in the altemative but equivatent forms: Z @-YRT_(h ) and = By Gi ') from which we find immediately for = 0 that “R(h-T) and Q ia -m= cr 1 5463.44 Isothermal case (5 = 1). Equations (3.35) and (3.36) are both indeterminate of form 0/0, Application of PHopital’s rule yields the appropriate results: P, Wa Ro and voctinit p(B) Adiabatic ease (5 = y). In this case simple substitution yields, 2)" ae Isochoric case (8 = 00). Here, simple substitution yields: W=0 md @Q An (2-1) = (2-!)-oa-m ~My ] men A What is needed here is an equation relating the heat transfer to the quantity of air admitted to the tank and to its temperature change. For an ideal gas ina tank of total volume V7 at temperature 7, ay oe Py! RF aT my The quantity of air admitted to the tank is therefore: ve Pi) n = w ‘The appropriate energy balance is given by Eq. (2.29), which here becomes: AAO ant Got WH = 0 where the prime (') identifies the entrance stream of constant properties, Multiplying by dé and inte- arating over the time of the process yields: aU, = m0, — n'H! = O With n =ms mW: — H) —m(U — H') = 0 Because Uz = Hz— RT and Ui =H — RT, this becomes: my — H! ~ RT) >> Cy, then Ts = Tj, If mC =0, then we recover the isentropic expansion formulas. 3.27 Foran ideal gas, AU =CyaT PV = RT APY) = RAT Whence, But 3.28 Since Z = PY/RT the given equation can be writen: Steer RT Differentiate atconsiant 7: dV =~ “Tap 6 my ‘The isothermal work is then: W -f pav=rr flap m sy Whi = ence, Wa RTh Compared with Eq, (3.26) 3.29 Solve th 3 ae .29 Solve the given equation of state for V Pa 60 P Rr 350Whence, By definition (Bq. (3.3)} Differentiate: By the equation of state, the quantity in parentheses is RT/P; substitution leads to [@,-F) G-#) 3.31 When multiplied by ¥/RT, Eq. (3.41) becomes: v aTyV/RT FV OY +00) a(D)V {RT oa THe Fayev Feab L__arye L stitute P= sel Sa) a Substimte P= Ver 255, RT Th eb ayoa teat 1 1+ bp + (bor +-- = bp Expressed in series form, the first term on the right becomes: The final fraction of the second term becomes: fesse Ieee a 1+ (€+0)bp + €a (bp) Soper —(€ tobe +(e +o) Combining the last three equations gives, afer reduction: a. _atry (<+0)a(T)] Pato GP)ae [PTE Equation (3.12) may be written: Z= 14 Bp-+ Cp? +-- Comparison shows: $81For the Redlich/Kwong equation, the second equation becomes: bal) _ ary oF olor ) =P cCah+ a RF Values for a(7) and b are found from Eqs. (3.42) and (3.43), with numerical values from Table 3.1 _ 0.08664 RT a(T) _ 0A2748RT. . Pe RT TP ‘The numerical comparison is an open-ended problem, the scope of which must be decided by the instructor, V+ 2C'P+3D'PP +. eae roo Equation (3.12) with V=1/p: Z=1+ Bp -+Cp?+ Dp + az 336 DitfremtateRa.(.1I (32) = 1, Whence, Z Differentiate: (2) =B+2Cp+3Dp? + a), Whence, (2), 8 Jao 3.56 ‘The compressibility factor is related to the measured quantities by Pvi_ MPY! 2 = RT ~ mT By Eq. 6.38), Boye = Sober w dz_dM dP dv! dm dT (a) By B4.(4), aa ada ae i 2 MTP TR WF o Thus Max 52% |Y5M + MS 4PL+ [%eSV"| + 1%5m + N87] Assuming approximately equal error in the five variables, a ++1% maximum error in Z requires errors in the variables of <0,2%, © By Eq. (8), dbz (ap BECO, 2 Za(F-4)+ ( ‘Therefore 952Max |% 5B) an |(w6se1+ reerr) 2z-1 FT| (m8 + 5841 + 5m) For 2 0.9 and for approximately equal error in the five variables, a 1% maximum error in B requires errors in the variables of less than about 0.02%. This is because the divisor Z— 1 * 0.1 Inthe limit as 2 —> 1, the error in B approaches infinity 3.57 The RedlielvKwong equation has the following equivalent forms, where a and 6 are constants: Vv +b) Wile a Poh RPRO +H z From these by differentiation, aZ\ _ a(V— by — RTP + by ( ) BU De OATES w a, RTAV BP + bP (3) a QV + bY — by ~ RTP PY + by? oy ay, TPP — bY + bY In addition, we have the mathematical relation aZ\ _ 2 /aV)r @), ~ GP/AM 2) Combining these three equations gives (2) aV(V — by? ~ bRDPYUV + by Tr OP), aRTQV FOV — by PAV + bP heal For P + 0, ¥ -> co, and Bq. (D) becomes: | lim (2 b= a/RTP , RT For P > 00, ¥ > b, and Bg, (D) becomes: 3.60 (a) Differentiation of Eg, (3.11) gives: az 4 20% pe aie (#), +2C'P +3D'PP+ hence Sim, Ifthe limiting value of the derivative is zero, then B’ = 0, and (®) For simple fuids, «o = 0, and Eq, (3.59) becomes B° = BP./RT.. If B = 0, then by Bg. (3.61), 0.422 o = 0.083 - Tr =0 5531 -(18 ba 0.085 3.X1 Figure 3.3 suggests that isochores (paths of constant volume) are approximately straight lines on a PT diagram, Show that the following models imply linear isochores: (a) Constant-. « equation for liquids. (b) Ideal-gas equation. (¢) Van der Waals equation. SOLUTION Linear isochores require that (8P/8T)y = Constant, we (o byt Gdapietwacosenr ces: (22) 2 w termites rr area (2) 8 o In each case the quantities om the right are constant, and so therefore is the derivative,Chapter 4 - Section B - Non-Numerical Solutions 4 For consistency withthe problem statement, we rewrite Eq. (4.8) as: B c (Co) = A+ SNH DESH HEED where Then 2/T\. Define Cry as the value of Cp evaluated a the arithmetic mean temperature Tx Chg = A+ Tam) + CTiy Te+T Tet) hth 2 2 2 and where 1 a Patsarty B Cae Whence, sie A+ ghee N+ GME +2 +h) Define & as the difference between the two heat capacities: Peetl P4204 3 4 This readily reduces to: Making the substitution r = 73/7) yields the required answer, 46 For consistency with the problem statement, we rewrite Eq, (4,8) as (Cr) B D AtSTetD+a Zhe D+ ae where ‘Then Ta) Ty, Define Cr as the value of Cp evaluated at the arithmetic mean temperature Toy, D Chg = A+ BTan + As in the preceding problem, Trt aeEeeTe Fog = EOE et = Beet gee 4 8 4D Whence, Cr = AF ST +1) $y 2NE+D+ rae ED Define 6 as the difference between the two heat capacities: (ict wr" aeaet D (z-1)? Te (eer, Making the substitution + = 72/7; yields the required answer. This readily reduces to:4.8 Except for the noble gases [Fig, (4.1)], Cp increases with increasing T. Therefore, the estimate is likely to be low. 4.27 (a) When the water formed as the result of combustion is condensed to a liquid produet, the resulting Jatent-heat release adds to the heat given offas a result of the combustion reaction, thus yielding a higher heating valuc than the lower heating value obtained when the water is not condensed. (6) Combustion of methane(g) with H)O(g) as product (LHV): Cis) + O2(g) + CO2x(g) A Hing = —393,509 2Ha(@) + Onle) > 242018) Aig = Q)(-241,818) CHa(g) > Cs) + 2H2(g) AH = 74,520 CH(g) + 203(g) > COn(g) + 2H:0(g) | AHS, = 802,625 3 LEV) Combustion of methane(g) with H,O() as product (HHV): (CHalg) + 202(g) > COx(g) + 220g) 2H:0(g) > 2H,0(1) CHa(g) + 20212) > COa{e) +2H200) | A Hig = ~890,649 J (HRV) (0) Combustion of n-decane() with H2O(g) as product (LH): 10.C(s) + 1002{g) > 10C02(g) AHigyg = (10)(~393,509) 11 Hx(g) + 5409(@) > 11 H,0(@) Hig = (11Y(-241,818) CioHa2() + 100(5)+ 11H2@) A HSgg = 249,700 6,345,388 J (LHV) CoHian(h) + 15403(@) > 10COx(g)+ 11 HO) | AHiy Combustion of n-decane(?) with H0(0 as produet (HAV): CioHaa(0) + 15L02(g) > 10 COs(g) + 11 HeO(e) AMq = ~6,345,388 11 HhO(e) > 1100) (1)-44012) CioHtaa( + 15}0:(¢) > 100%) +1100 [AMS 520 1 (HEV) 556Sal 56 SAL Chapter 5 - Section B - Non-Numerical Solutions Shown to the right isa PV diagram with two adiabatie Hines | > 2 and 2 — 3, assumed to inter- sect at point 2. A cycle is formed by an isothermal line from 3 —> 1. An engine traversing this cycle p would produce work. For the eycle AU = 0, and therefore by the first law, O + 1 = 0. Since W is negative, Q must be postive, indicating that heat is absorbed by the system. The net result is therefore a complete conversion of heat taken in by a cyclic process into work, in violation of Statement 1a of the second law (Pg. 156). The assumption of intersecting adiabatic ins is therefore false. Imtersecting adiabatics| ‘The energy balance for the over-all process is written: Q— AU" + AEx + ABp Assuming the egg is not scrambled in the process, its intemal-energy change after it returns to its initial temperature is zero. So too is its change in kinetic energy. ‘The potential-energy change, however, is negative, and by the preceding equation, so is Q. Thus heat is transferred to the surroundings. The total entropy change of the process is: ASioai = AS' + AS! Just as AU’ for the egg is zero, so is AS". Therefore, Qesuce AS = BShag = = Since Q is negative, A Siu: is positive, and the process is irreversible. By Eq, (5.8) the themmal efficiency ofa Camot engine is: re : one eae Differentiate: (ino _OM Since To/Ti is ess unity, the efficiency changes more rapidly with Te than with Ty. So in theory itis more effective to decrease Te. In practice, however, fc is fixed by the environment, and is not subject, to control. The practical way to inctease m is to increase Ty. Of course, there are limits to this to. For an ideal gas with constant heat capacities, and for the changes T, > Ts and P, > Ps, Eq, (5.14) can be rewritten as a e AS=Crin(2) — rin(2 c »(2) en(2) (if PR =P, AS; =crin (2) Ir h=h, i h h ty Whence, Asy =Cpln(2)—rin( 2) =cym(2 a nF) -en(F) = "(7)Since Cp > Cy, this demonstrates that ASp > AS,. a (Pt x Of B=T, ASp=—Rb ( ') If he toe Whence, AS =Cpin(2) ~ rin (®) = 0, n(2 : a (3) : (2) non ‘This demonstrates that the signs for ASp snd A Sy are opposite 5.12 Start with the equation at the top of Page 167: as CK aT CHaT dP RoR TR Te Foran ideal gas PY = RT, and InP+InV¥ =InR+InT. Therefore, aya dry ap ar av i Pee i ape v Whence, Because (Cif/R)—1=CHE/R, this reduces to car char y Raritan AS plc#ar | ¥ tnegtin yi sf $n) As an additional part of the problem, one could ask for the following proof, valid for constant heat capacities. Return to the original equation and substitute dT/T —dP/P + d¥/¥: 43 _ char, chav ap_ citar , car y Yeresey Tau steevaty Jeet Aetete) JeentedSeet diatads Saat 2 Integration yields 13 As indicated in the problem statement the basic differential equations are: dW —dQy ~dQc (4) Qn Te 0c 7 Te (8) where Qc and Oy refer to the reservoirs. 558.(@ With dQx=CydTy and dQc = ChdTc, Eq, (B) becomes: CydTy TH CedTe Te Whence, din Te = Wd In Ty Integration from Ty, and To, to Ty and Te yields: To _ (tu) * Hee ere m= Gg) [e=m(H) ©) With dQy—ChdTy and dQ = ChaTo, Eq. (A) becomes: AW = CydTy + Ch Te Integration yields: W = Ci(Tn ~ Tag) + Co(Te ~ Tey) Eliminate T- by the boxed equation of Part (a) and reatrange slightly: ~ W = Cit (FE -1) + 08% [(%) : | (©) For infinite time, Ty = Te = T, and the boxed equation of Part (a) becomes: ron (i)-a((9) From which: TH 2 Tes (Tig)* T= (Teg (T yee se Tes MOD (Ty OVA Because ¥W/(W + 1) — 1 =—1/( + 1), then: yr ae Because Ty = 7, substitution of these quantities inthe boxed equation of Part (6) yi ae [(@)"" ‘| +C6Tey iq” = ] las: w 5.14 As indicated in the problem statement the TH basic differential equations are: aW —dQy~dQc=0 (4) aw 4Qu Tn dQc Te i) where Qc and Qy refer to the reservoirs.(@) With dOc =CedTe, Eq. (B) becomes dQn __™ ChaTe ~~ Te Substitute for dQ, and dQc in Eq. (4): or aw Integrate from To, to Te: Te Te Zl We=—CLTyIn = + CL(To To.) oF w= C6 (twin + r0~ 1) Tey Te (6) For infinite time, Te = Ty, and the boxed equation above becomes: rR w= c¢ (ruin 2 + Ty ~ Be) Tr 5.15 Write Eqs. (5.8) and (5.1) in rate form and combine to eliminate | | Te VA ig Fair Top TW 1Gl where r= With 1Ocl = kA(Te}! = kA(r Tu)", this becomes: A(Tyy* ual kA(Tyys of A= APh(Tyy A [aes Differentiate, noting that the quantity in squate brackets is constant: df Ww 3 1 _ | ar —3 a | kaa [Sr wl- Kt | La=rPA Equating this equation to zero, leads immediately to: 4r =3 or 75 5.20 Because W = 0, Bg. (2.3) here becomes = AU! =mCyar ‘A necessary condition for AT to be zero when Q is non-2er0 is that m = 90. This isthe reason thet natural bodies (air and water) that serve as heat reservoirs must be massive (oceans) oF continually renewed (rivers) 5.22 An appropriate energy balance here is: Q = AH' =0 Applied to the process described, with Tas the final temperature, this becomes: mT + mT mCrT ~T)) +mCp(T — Ts) =0 whence my +m w msm, T= i+ ty/2 5603.23 5.24 531 ‘The total entropy change as a result of temperature changes of the two masses of water: r r = myCrln = +m Crin 2 AS =mCeln ge +mCeln ® Equations (1) and (2) represent the generat case. If m= mz =m . r AS = mOpn=e or A Because T= (T+ 13)/2> VTS, AS" is positive Isentropie processes are not necessarily reversible and adiabatic. The term isentropic denotes a process for which the system does not change in entropy. There are two causes for entropy changes in a system: The process may be internally irreversible, causing the entropy to increase; heat may be trans: ferred between system amd surroundings, causing the entropy of the system to increase or decrease. For processes that arc intemally irreversible, itis possible for heat to be transferred out of the system. in an amount such that the entropy changes from the two causes exactly compensate each other. One can imagine irreversible processes for which the state of the system is the same at the end as at the beginning of the process. The process is then necessarily isentropic, but neither reversible nor adiabatic. More generally, the system conditions may change in such a way that entropy changes resulting from temperature and pressure changes compensate each other. Such a process is isentropic, but not necessarily reversible. Expansion of gas in a piston/cylinder arrangement is @ case in point. It may be reversible and adiabatic, and hence isentropic, But the same change of state may be irreversible with heat tranafer tothe surroundings. The process is still isentropic, but neither reversible tor adiabatic ‘An isentropic process must be either reversible and adiabatic or irreversible and non-adiabatic. GCedt [Cod T-% h-T By inspection, one sees that for both T > T) and 7; > T the numerators and denominators of the above fractions have the same sign. Thus, for both eases (Cp), is positive. tod Coe SRO WTR ~ Inche/TY By definition, (Coly larly, (Cols By inspection, one sees that for both T > Ty and Zo > T the numerators and denominators of the above fractions have the same sign, Thus, for both cases (Cp), is positive. When T = Tp, both the numerators and denominators of the above fractions become zero, ard the fractions are indeterminate. Application of ! Hopital’s rule leads to the result: (Cp)yy = (Cp)s = Cp. The process involves three heat reservoirs: the house, a heat sink; the furnace, a heat source; and the surroundings, « heat source. Notation is as follows: |Q| Heat transfer t the house at ermperature T \Qr| Heat transfer from the furnace at Ts 1Q.| Heat ransfer from the surroundings at T, ‘The first and second laws provide the two equations: | = |Or| + 1Qah and. eae 361‘Combine these equations to eliminate |Q,1, and solve for |r! ~ jo ( Pom) Te \ori=10(2—= %) With T=295K Tr = 810K T, = 265K and |Qj = 1000 k} The result is: 1Qe| = 151.1410 Shown to the right is a scheme designed to accomplish this result. A Carnot heat engine operates with the furnace as heat source and the house as heat sink. The work produced by the en- Tori sine drives a Carnot reftigerator (reverse Carnot engine) which extracts heat from the surroundings and discharges heat to the house. Thus the hreat rejected by the Carnot engine (|Q1]) and by the Camot refrigerator (|Q21) together provide the heat |Q| for the house, The energy balances for the engine and refrigerator are Wiegiae = |e! — 1Qrl \hetis = 102] ~ 1x1 Equation (5.7) may be applied to both the engine 1el sand the refrigerator: SURROUNDINGS @ T, Wel te It _ FURNACE @ Tr ial 7 1a 7 Combine the two pairs of equations: Whom = 108% — ) Since these two quantities are equal, Tr- tr 10x17 = 10a or Oa = 10a Because the total heat transferred to the house is |Q| = 1011 + 1Qal, a Te-T Te-T\ _ 9 Te-Te |Ql = lal + Onl on (1+ Fe) 0 r T (Te But 101 = |Orlzz whence 10l= one (2) Solution for [Or yields the same equation obtained more easily by direct application of the two laws, of thermodynamies to the overall result ofthe process. 8.32 The process involves three heat reservoirs: the house, @ heat source; the tank, a heat source; and the surroundings, a heat sink. Notation is as follows: $62|Q Heat transfer from the tank at temperat |Q'| Heat transfer from the house at 7” [Q| Heat transfer to the surroundings at 7, ‘The first and sevond laws provide the two equations: 11+ |O1= 106 and ‘Combine these equations to eliminate |Qq|, and solve for |Q: With = T=448.15K 7 306.15 K 2w7IsK =, The result is: 1Q| = 143.38 ks ture T Izl_ 19 121 _y and |Q"| = 1500 83 TANK@T | ‘Shown tothe right is a scheme designed to accomplish this result. A Camot heat engine operates with the tank as heat source and the surroundings as heat sink. The work produced by the engine drives a Camot reftigerator (reverse Camot en gine) which extracts heat |Q'| from the house and discharges heat to the surroundings, The energy 191 balances for the engine and refrigerator are: SURROUNDINGS @ T, (Fleagine = 12| — 1Qe,1 [Whesis = |Qx| ~ 10'1 Equation (5.7) may be applied to both the engine and the refrigerator: Woy _ Te IQal _ To le! lel T oi 7 HOUSE @ T' Combine the two pairs of equations: (Weexe = 101(1 #)-10* Since these two quantities are equal, 10-5 ® ~oiB5* or 12.-101( T537 $40 where Q; is here redefined to refer to the system rather than to the surroundings. Nevertheless, the sec= cond term accounts forthe entropy changes of the surroundings, and can be written simply as dSty,/d: a(mS)ev — Shae ASy Sher _ g ar ninaaat a Sar detasl tee Multiplication by d end integration aver finite time yields ASS, + MS, = 0 or AS = 0 The general equation applicable here is Eq, (5.22): (@) Fora single stream flowing within the pipe and with a single heat source in the surroundings, this becomes (asi 2s, 20 z (0) The equation is hete writen fortwo steams (I and I) flowing in two pipes. Heat tans is internal, beloeon the two sueams, making Q — 0. Ths, (Sun + (AS)urin = Se = 0 (©) For a pump operatiing on a single stream and with the assumption of negligible heat transfer to the surroundings (AS = So 20 (@) For an adiabatic gas compressor the result is the same as for Part (c). (©) For an adiabatic turbine the result is the same as for Part (c). (D For an adiabatic throttle valve the result is the same as for Patt (c) (g) Foran adiabatic nozzle the result is the same as for Part (c) ‘The figure on the left betow indicates the direct, irreversible transfer of heat |Q| from a reservoir at 7; (o a reservoir at 7;. ‘The figure on the right depicts a completely reversible process to accomplish the same changes in the heat reservoirs at T; and T: ni R Hl lal 564The entropy generation for the direct heat-transfer process is: 80 ~101(3 - 7) -101(452) For the completely reversible process the net work produced is Wise (2% N-h ant = Wh Hi} Te101(S SB) This is the work that is lost, Wig, in the direct, irreversible transfer of heat |. Therefore, nat wim o\(2EB) ant ins plas Rh Wea = To| Ql TeSc Note that a Carnot engine operating between 7; and 7; would not give the correct Wigeat Of ios. because the heat it transfers to the reservoir at 73 is not Q. 5.45 Equation (5.14) can be written for both the reversible and irreversible processes: bead ar ie Tw aT ee eS it yh =f cen? asmn= [FS ng AS f c#Z -0t By difference, with AS = 0 ce - Since A Sipe, must be greater than Zero, Tiney must be greater than Try 565Chapter 6 - Section B - Non-Numerical Solutions 6.1 By Eq. (6.8), and isobars have positive slope ite terse satis (22) = (22) coninwinreccin: —[( Cates tee sae ces wo 6.2 (a) Application of Eq, (6.12) to Eq. (6.20) yields: aCe) _ fav —TEr/ar») oP), | ar E . (22),-(0),-108), Gr Whence, For an ideal gas’ and (Fe =0 > (2) Equations (6.21) and (6.33) are both general expressions for dS, and for a given change of state both must give the same value of dS. They may therefore be equated to yield: (ar a), iB) [P reviswamane — [er=erar(22) (2) Hoy ma (22) 8 By Eqs. (3.2) and (6.34): (#) =» and (3), . Contin watered sauton: [cy 6r =ar7 (2) 6.3 By the definition of H, U = H — PV. Differentiate: au) _ (aH ar Gr), @), °(% ete 366Substitute forthe final derivative by Eq. (3.2), the definition of B: ar. (22) -ce-arv Divide Eq. (6.32) by a7 and restrict to constant P. The immediate result is: OO A®, Solve for the two derivatives by Eqs. (6.34) ond (3.2); substitution gives: 6.4 (a) In general, By the equation of state, tees seesEaCE (F), Crt Leer a | aaa “¥=6b Substituting this derivative into Eq. (6.32) yields dU = Cy dT, indicating that U = f(T) only, (6) From the definition of H, From the equation of state, dH =dU +a(PP) RdT + bdP dPV) Combining these two equations and the definition of part (a) gives: dH = Crd? + RaT + bdP = (Cy + RAT + baP ‘Then, (# ar), =Cy4R By definition, this derivative is C'p. Therefore Cp = Cy +R. Given that Cy is constant, then 80 is Cp and so is CriCv, (0) For a mechanically reversible adiabatic process, dU = dW. Whence, by the equation of state, CydT =—PdV = But from part (b), R/C) av T dinT =~(y —I)dinly ~ 6) From which: aT. rae Rm Bday ~ 6) (Cr —Cr/Cr or Then dint +diny ~ oy! =0 TY — by = const Substitution for 7’ by the equation of state gives PU ~ 6) ~ by R = const. 367 or68 It follows immediately from Eq. (6.10) that: ac v¥=(— and Gr), Differentation of the given equation of state yields: RT arr) pet TO) ainp v P and Ss ar Once V and (as well as G) are known, we can ppl the equations H=G+Ts and U=H-PV=H-RT ‘These become " anny eae ar(T) a H=r TT and u=T(7) TF RT By Eqs. (2.16) and (2.20), aw ud pee c= (5), Because Fin a faneton of temperature only, these become er é cu oe ‘The equation for ¥’ gives the ideal-gas value. The equations for A and U’ show these properties to be functions of 7 only, which conforms to ideal-gas behavior, ‘The equation for $ shows its relation to P to be that of an ideal gas. The equations for Cp and Cy show these properties to be functions af T only, which conforms to ideal-gas behavior, as does the result, Cp = Cy + R, We conclude that the given equation of state is consistent with the model of ideal-gas behavior. 66 It follows immediately from Eq. (6.10) that: aG ”- (5), _ Differentation of the given equation of state yields: aG at), K and S= Once V and $ (as well as G) are known, we can apply the equations: H=G4+TS and U=H-PVY=H-PK These become: a : eo) and v= Fr)- TE Ha F(T) +KP— (y+ KP 1 i- By Bgs. (2.16) and (2.20), co=(#8) at 568,Because F isa function of temperature only, these became: @P C= and ‘The equation for V shows it to be constant, independent of both T and P. This is the definition of ‘an incompressible fluid. H is seen to be a function of both T and P, whereas U, S, Cp, and Cy are functions of T only, We also have the result that Cp = Cy. All of this is consistent with the model of an incompressible uid, as discussed in Ex. 6.2. 6.11 Results for this problem are given in the text on page 213 by Eqs. (6.59) and (6.60) for G® and #7 Bq, (6.45), page 206, then yields 5 6.12 Parameter values for the van der Waals equation are given by the first line of Table 3.1, page 99. At the bottom of page 214, itis shown that J = f/Z. Equation (6.63b) therefore becomes: GF RT a6 Zz = 1-1 =p) — For given T and P, Z is found by solution of Eq, (3.49) for a vapor phase or Eq. (3.53) for a liquid phase with o = =0. Equations (3.50) and (3.51) for the van der Waals equation are: Be 2 E ond - With appropriate substitutions, Eqs. (6.64) and (6.65) become: He 9B RT fas Zz 7 and | = mz—A) {6.13 This equation does not fall within the compass ofthe generic cubie, Eq. (3.41): so we start anew. Fist, ‘multiply the given equation of state by /RT: Substitute: z ‘Then, z Because p = P/ZRT, Given T and P, these two equations may be solved iteratively for Z and & Because 4 is a constant, Eys. (6.57) and (6.58) may be rewritten as: 569Gt S [@-vE+2-1-mz @) HR _ ft (az) ag wo f (BB+ © In these equations, Z is given by Eg, (4), from which is also obtained: az Inz=—mn1—g)—9& and (3) 7 nes exp(-48) I The integrals in Eqs. (B) and (C)) must be evaluated through the exponential integral, E(x), @ special function whose values are tabulated in handbooks and are also found from such software packages as MAPLE®. The necessary equations, as found from MAPLE®, are: 5 dl fe nF = ep-atet-et—91- 2-9) £48 Ines) — 7 where y is Buler’s constant, equal ro 0.57721566. " az) st and at) (FZ) F=aecaei-gd—p-B-9} har) Once values for G2/RT' and H®/RT are known, values for $*/R come from Eq. (6.45). The diffi- euler of integration here are one reason that cube equation have found pester vor. 6.18 Assume the validity for purposes of interpolation of Fg. (6.70), and write it for Ts, and 7) mre aa 2 (a) inp aa ; (8) inp =a © samaicrimay nla (2 samen —wher(L 1) asf =1 ‘The ratio of these two equations, upon rearrangement, yields the required result 6.19 Write Eq, (6.70) in logyg form log P= A “ Apply at the critical point log P. = (8) i sie 570By difference, log P= B (; eS 7) -B (@ a *) © Whence, Equation (C) then becomes fee G *) ( Apply at T; = 0.7: IogtP) 5 By Ea. 0.49), = -1.0— log?) e027 Whence, (fa)men= 6.83 The slopes of isobars and isochores on a T'S diagram are given by Eqs. (6.17) and (6.30): ar) _ : ar) _ 7 B5)_~ Ce a 35 )y Sy Both slopes are necessarily positive, With Cp > Cy. isochores are steeper. An expression for the curvature of isobars results ftom differentiation of the first equation above: (z 21 (a) 7 (ace) 7 _ 1 (aCe) (aT) _ Py, 7 (aCe as), Cre\aS), CRIS} 3 Var ),\as),~ CRU” Ce Var J. acer __or a aT), ae BT ator win craaser, (35) =m and 1-£( Because this quantity is positive, so then isthe curvature ofan isobar. 6.84 Division of Bq. (6.8) by dS and restriction to constant yields: an a (22) <7+7(%2),—aweavas, @ as), Therefore, smAlso, 29)(3) 80) G8) Whence, By Fas. (3.2) and (3.37) ay (F), and av) _R dB wi a) 54S ani hence, (3), Bt id Differentiation of the second preceding equation yields: ap R R dB\ 1 (av (B)--s- GB) AG) av) __Rr From the equation of state, ( 3), --2 ®)__ Rk BRT OR Whence, (35), <- yet he Ret) Clearly, the signs of quantity (BT — 1) and the derivative on the left are the same. The sign is determined from the relation of f and ¥ to B and dB /dT’ 1 (R, 4B > pr -F(5+F)-1= In this equation dB /dT is positive and B is negative, Because RT/P is greater than |B, the quantity BT ~ 1 is positive. This makes the derivative in the first boxed equation positive, and the second derivative in the second boxed equation negative. Since a reduced temperature of 7; = 2.7 is well above “normal” temperatures for most gases, we expect on the basis of Fig. 3.11 that B is (—) and that dB/dT is (+). Moreover, d?B/dT? is (~). By Eqs. (6.53) and(6.55), G®=BP and. S*# = —P(dB/dT) Whence, both G* and $? are (). From the definition of G8, H® =G"+TSS, and H¥is(-) By Eqs.337) and (640, Y= B, and V*is(-). ‘Combine the equations above for G*, 8, and H*: ata P(a—1 2) whence, (3 ) ar. anes Therefore, C2 = ( es *). is(4). (See Fig. 65.)Non-Numerical Solutions Chapter 7 - Section B 7.2 (a) Apply the general equation given in the footnote on page 260 to the particular derivative of interest here: ar (2 as. oP}, a5), \oP J, The two partial derivatives on the right are found from Eqs. (6.17) and (6.16); thus, (2) Tr (2) For gases, this derivative is positive. It applies to reversible adiabatic expansions and compressions in turbines and compressors. (6) Application of the same general relation (page 260) yields: (5), Go), Gr), ‘The two partial derivatives on the right are found from Eqs. (2.16) and (6.31); thus, (or), =e-[? *(),] For gases, this may be positive or negative, depending on conditions. Note that itis zero for an ideal gas. It applies directly to the Joule expansion, an adiabatic expansion of gas confined in a portion ofa container to fill the entire container. 7.3. The equation giving the thermodynamic sound speed appears in the middle of page 250. At written, it implicitly requires that V represent specific volume. This is easily confirmed by a dimensional analysis. If V is to be molar volume, then the right side must be divided by molar mass; v? (ap ¢=-x la), ‘a Applying the equation given in the footnote on page 260 to the derivative yields: Gr), ~~ (3s), (3), (), 1G), GG). (1G), 1G), @),] Division of Eg. (6.17) by Eq, (6.30) shows that the first product in square brackets on the far tight is, the ratio Cp/Cy. Reference again to the equation of the footnote on page 260 shows that the second product i square brackets on the far right is ~(@P/@V)r, which is given by Eq. (3.3). ‘Therefore, 3) -2 (3) ce (3) Is Cy NAV Jy Cy NeW. W, 573vCp ~ MCye Substitute into Eq, (4) (a) For an ideal gas, Y = RT/P and x = 1/P. Therefore, @®) For an incompressible liquid, ¥ is constamt, and x = 0, leading to the result: ¢ = oo. This of course Icads to the conclusion thatthe sound speed in liquids is much greater than in pases. 16 1 1 : : CCritical-pressure ratio Po/Py ‘As Pr decreases fom an initial value of P; = Pi, both up and sr steadily increase until the critical~ pressure ratio is reached. At this value of Pp, zp equals the speed of sound in the gas, and further reduetion in Pz does not affect 2 oF 7.7 The mass-flow rate rn is of course constant throughout the nozzle from entrance to exit, ‘The velocity u rises monotonically from nozzle entrance (P/P; = 1) to nozzle exit as P and P/P, decrease. ‘The area ratio decreases from 4/4; = 1 at the nozzle entrance to & minimum value at the throat and thereafter increases to the nozzle exit, 7.8 Substitution of Eq. (7.12) into (7.11), with m; = 0 gives: 2 ( 2 ) ( 2 ) eeat = 1-——) = van (— thea = pat) 7h (Sa and P; isin Pa. The units of ty ae then where V1 is specific volume in m?-kg™ ‘akg m-s With respect to the final term in the preceding equation, note that Pj V has the units of energy per unit ‘mass, Because I N-m = 1 J, equivalent units are J-kg™!. Moreover, P.¥) = RTi/M; whence With 2 in units of J-(kg mol)"-K-!, RT;/M has units of F-kg~ S747.46 It is shown at the end of Ex, 7.5 that the Joule/Thomson inversion curve is the locus of states for whieh (8Z/9T)p = 0. We apply the following general equation of differential calculus ),-@).+@),@), (),= Ga), G(r), Yn (37), - Ga), @), Ge), ae P a) Pf -l az mone paper, pn zhao (8) -2(c2.[eur(%) Setting (0Z/0T)p = 0 in each of the two preceding equations reduces them to: (BG), Ronit (),-- (3), G2), a7), "za F Combining these two equations yields: &) a), (@) Equation (3.41) with van der Waals parameters becomes: ara “V¥=6b FF P Multiply through by /R7, substitute Z = PV/RT, V = 1/p, and rearrange: 1 ae 1b RT In accord with Bq, (3.48). define q = a/bRT. In addition, define § = bp, Then, Zz 9 (ay ae : az ‘az ee (=),- (GF), By Eg. (3.43) with @(T,) = | for the van der Waals equation, q a V(t) ar nal) (=), W/QT,. Whence, Then, In addition,‘Substitute for the two partial derivatives in the boxed equation: rit _be Pape a Whence, @ By Eq, (3.43), Pe = QRT./b. Moreover, P = ZpRT. Division of the second equation by the first gives B, = ZpbT'/ QT... Whence zer, 7 © These equations allow construction ofa T; vs. P; inversion curve as in Fig. 72. For a given value of 7,, calculate q. Equation (B) then gives &, Eq, (4) gives Z, and Eq. (C) gives P,. (©) Proceed exactly as in Part (a), with exactly the same definitions. This leads to a new Eq. (4): R eee CITE Tee a. By Eq. (3.43) with a(T;) — 7,95 for the Redlich/Kswong equation, ¢ = Wi/S27;!5, This leads to: dq __1Sq : az) _ _1Sg ated be at),~ Ta+5 Moreover, (2) ees op), G-sF + kP Substitution of the two derivatives into the boxed equation leads to a new Eq, (B) 14ey) 1 ) (4) (are @ ‘As in Part (a), for a given 7, calculate q, and solve Eq. (B) for &, by trial ora by @ computer routine. As bofore, Eq. (4) thon gives Z, and Eq. (C) of Part (@) gives 2, 7.A7 (a) Equal to, (6) Less than. (c) Less than. (a) Equal to. (e) Equal to 7.28 When a saturated liquid is expanded in a turbine some of the Liquid vaporizes. A turbine properly 1, the derivative is negative (try some values). Thus, the work of compression decreases as C’p increases and as the molecular complexity of the gas increases. 74S. The appropriate energy balance can be written: W = AH —Q. Since Q isnegative (heat transfer is ‘out of the system), the work of non-adiabatic compression is greater than for adiabatic compression. Note that in onder to have the same change in state of the ai; ie, the same AH, the irreversibilities of operation would have to be quite different for the two cases. 7.46 There is in fact no cause for concem, a adiabatic compression Sends the steam further into the superheat region. S78Chapter 8 - Section B - Non-Numerical Solutions 8.12 (a) Because EQ. (8.7) for the efficiency noice includes the expansion ratio, re this quantity to the compression ratio, r = Vc/ ¥p, and the Diesel cutoff ratio. re Vo = Vay r= VciVs. Whence, 1 Vg, we relate 141 Vo. Since r _VelVo _ Ya 2 Ve[Va Vo Equation (8.7) can therefore be written: 3 [ewe aver) _ Ltn (a Toes vb rear yr | 1") ot 7 | mea =1~ (5) wa (®) We wish to show that ease ae) end 7-0” 1 I or more simply Taylor's theorem with remainder, taken tothe Ist derivative, is written g=all)+2'0)-@-)+R eT +6@—1) where, @-1) @ Land x > 1, R > 0. Therefore: x >14a-(e-1) bas ve) (@ Ity = Land = 8, then by Ea. (8.6 yes -(3) and yh guy : ty Sand [vines = 0.4904 (i) caer mt [tome 0 et yey - (3) Geos [oe = 04007 f-1>a-(e-1) 5647 i8.15. See the figure below. In the regenerative heat exchanger, the air temperature is raised in step B > B*, while the air temperature decreases in step D > D*. Heat addition (replacing combustion) isin step Bac Bip Wen ition, ” a One where, Was = (He ~ Ha) = Co{T's — Ta) Wen = (Hp — He) = Cp(Tp — Te) Oarc = Cp (Te — Ty) = Co(Te ~ Tp) Ty—Ta+Te~To Tr -Ts Whence, peeesstDy ty a Te~To Te Tp By Eq. (3.296), mi nan (2) =n (2) ‘Then, ql Multiplication of numerator and denominator by (Ps/P.)("~” gives: el) 580Chapter 9 - Section B - Non-Numerical Solutions 9.1 Since the object of doing work |H’| on a heat pump is to transfer heat [Qy7/ to a heat sink, then: What you get = |u| ‘What you pay for = {77 1Qu! Whence @ = 20 Wi For a Camot heat pump, Qa Ta ° Iai 1Oci~ Tw Te 9.3 Because the temperature of the finite cold reservoir (contents of the relfigerator) is @ variable, use differential forms of Carnot’s equations, Eqs. (5.7) and (5.8): eae and awe 4c Te In these equations Oc and Oy refer to the reservoirs. With dn = Cl dTo, the first of Carot’s equations becomes: ) E)a0n Ty be ae 4g, are i Te Combine this equation with the second of Camot’s equations: ~CTy ae aW = -C'Ty +0 dTe Te Integration from To=Ty to Te = Te yields: tee eee tate W = Cty WE + Ce Ty) 8 ct (1 B+k | 9.5 Differentiation of Eq, (9.3) yields Be Te buy aeiacirgt (=) i (in). Ty TP Because Ty > Tc, the more effective provedure is to increase Te. For a real refrigeration system, increasing Te is hardly an option if refrigeration is equired at a patic- ular Value of Tc. Decreasing Ty is no more realistic, because for all practical purposes, Ty is fixed by environmental conditions, and not subject to conto Ty Te OF 9.6 Fora Camot refrigerator, a is given by Bq. (9.3). Write this equation for the two cases: Te e and Tw -Te Because the directions of heat transfer require that Tyr > Tay and Tc < Tyo, a comparison shows that © < @, and therefore that « is the more conservative value, 58Chapter 10 - Section B - Non-Numerical Solutions 10.5 For a binary system, the next equation following Eq. (10.2) shows that P is linear in x}. Thus no ‘maximum or minimum can exist in this relation. Since such an extremum is required for the existence ‘of an azeotrope, no azeotrope is possible. 10.6 (a) Because benzene and toluene are chemically simitar and the pressure is only l(atm), this system can be modeled by Raoult’s law to a good approximation, (®) Although n-hexane and n-heptane are chemically similar, a pressure of 25 bar is too high for ‘modeling this system by Raoult’s law. (©) At 200 K, hydrogen is supercritical, and modeling the hydrogen/propane system at this temper ture by Raoult’s law is out of the question, because no value of P “for hydrogen is known. {d) Because isooctane and n-vetane are chemically similar and at a temperature (373.15 K) close 10 their normal boiling points, this system can be modeled by Raoult’s law to a good approximation, (e) Water and n-decane are much too dissimilar to be modeled by Raoult’s law, and are in fact only slightly soluble in one another at 300 K. 10.12 For a total volume of an idesl gas, PI = RT. Multiply both sides by y;, the mole fraction of species jin the mixture: mm; LRT mM yPVi =m RT or p= where m; is the mass of species /, M, is its molar mass, and p, is its partial pressure, defined as i =P. Solve for m; RT Applied to moist air, considered a binary mixture of sir and water vapor, this gives ng a MiOPHOK' ag Mucpas¥! = RT (a) By definition, = Tie or ha (#) Kfairis in equilibrium with liquid water, then the partial pressure of water vapor in the air equals the vapor pressure ofthe water, and the preceding equation becomes: Pet wpe — Mino Fit. Ma % 582(c) Percentage humidity and relative humidity are defined as fatlows: and A _ pag PRs —= oe == (100) Fe PR Pro Combining these two definitions to eliminate pro gives: ps PPR Gra/100) 10.14 Because the vapor space above the liquid phase is nearly pure gas, Eq. (10.4) becomes P = x7 For the same mole fraction of gas dissolved in the liquid phase, P is then proportional to 1. Values aiven in Table 10.1 indicate that were air used rather than COz, P would be about 44 times greater, ‘much too high a pressure to be practical 10.15 Because Henry’s constant for helium is very high, very little of this gas dissolves in the blood streams. Of divers at approximately atmospheric pressure. 10.21 By Eq. (10.05) and the given equations for In y; and In y2, AP = xy exp(txd) Pt and yeP =x explaad) Pg ‘These equations sum to give: Px exp(and) PS xp exp(axt) Py Dividing the equation for y; P by the preceding equation yields: srexplar Pmt a expCA) PS + mz expla PS _xz this equation obviously reduces to: p= pot PR 10.23 A little selection should convince anyone that there is no other way that BOTH the liquid-phase and. vapor-phase mole fractions can sum to unity 10.24 By the definition of a K-value, y; = Kixr and yz = K>x2. Moreover, y; + y2 = 1. These equations combine to yield: Kurt Kon = 1 or Kyxy+ Ka(l =) = i-k Solve for xy x Substitute for.x; in the equation yy = Kix Ki — Ka) 583,Note that when two phases exist both x, and yy are dependent of 2 By a material balance on the basis of | mole of feed, silty =z or x -Vy+ nV Substitute for both xy and yy by the equations derived above: Kil = Ka) i= ky Rett Ven (Ki Solve this equation for V Da Note that the relative amounts of liquid and vapor phases do depend on 21. 584Chapter 11 - Section B - Non-Numerical Solutions 11.6 Apply Eq, (11.7) iaecleatet ee) Fa lien"? Cah, 11.7 (a) Let m be the mass of the solution, and define the partial molar mass by: Let My be the molar mass of species k. Then m= DmMia=nMit DM; G4i) i Pr"... Whence, rie = M, | (Bane (oom ee aaa eee (3st! i= (Tr), oe If.M, is the molar mass of species 7, "TA Whence,119 For application of Eg. (11.7) all mole fractions must be eliminated from the given equation by the relation x; = mf nM = My + 1nMz + 3Ms + weet, (ACIDY ea tne 83) td Peaaas eNO rma, Because n =m; 4m +, (#) 1 Tr Pasay = My+ xml] ~ 21 Mrtxsfl—2m}C| and | My = My txyan[1 —225]C ence, = M+ 2 [1 wi mB uM, Similarly, ‘One can readily show that application of Eq, (11.11) regenerates the original equation for Mf. The infinite dilution values are given by. Me =M+xmuC kD Here-x; and xy are mole fractions on an i-free bass. 11.10 With the given equation and the Dalton’s-taw requirement that P = S>) p,, then: pa yn, For the mixture, P= ZRT/V. These two equations combine to give Z = Ty y1Zi. 11,11 ‘The general prineple is simple enough Given equations that represeat partial properties &%,, Sf", or SP as functions of com position, one may combine them by the summability relation to yield a mixture property Application ofthe defining (or equivalent) equations for partial properties then regenerates the given equations if and only ifthe given equations obey the Gibbs/Duhen equation. 11.12 (a) Multiply Eq. (4) of Ex. 11.4 by m (= mj +2) and eliminate xy by xy = m/(n1 + na) nfl = 600(m, + m2) ~ 180m ~ 207 — Form the partial derivative of mf with respect to m at constant ny an ant cn ao ao Gy tmyP tm) 00 - 180-20] ]=s20- 00 + 40 Whence, 60x +40x} Form the partial derivative of mH with respect to nz at constant or(8) Im accord with Eq. (11.11), H = (420 ~ 60.5? + 40.x}) + (1 — 22)(600 +4029) Whence, H = 600 180x; ~ 20x} ath (©) Write Ba. (11.14) fora binary ystem and divide by days PE 4 4 SP ay Differentiate the the boxed equations of part (@) dh ae ath 7 dey PHD} = 120.29 and FT = 12049 ‘Multiply each derivative by the appropriate mole fraction and add: 1200382 + 120891 = 0 (@) Substitute x, = 1 and x, = 0 in the first derivative expression of part (c) and substitute xj — 0 in the second derivative expression of part (c). The results are: (Si), (@), ath © 11.13 (@) Substitute x2 = 1 — x; in the given equation for V and reduce: : Apply Eqs. (11.15) and (11.16) to find expressions for Fs and Vs. First, av O = 58-Im, — 2a? dx; se Then, 2oxt tax} | and +x | 587(b) In accord with Eq. (11.11), rp 1128 — 2x1 — 2047 + 4x9) + 1 —41)(00 4x3 + 14x) 10 Whence, ¥ 8.41 which is the first equation developed in part (a), (6) Write Bq, (11.14) for a binary system and divide by dy Differentiate the the boxed equations of part (a): 27) gage + 4rxt and Oe Max +4237 dx “Multiply each derivative by the appropriate mole fraction and add xi(-2 = 40x, +427) + (1 —11)(2x) +427) =0 TThe validity of this equation is readily confirmed. (@) Substitute x; — 1 in the first derivative expression of part (c) and substitute x; = 0 in the second derivative expression of part (c). The results are: © UL14 By Eqs. (11.15) and (11.16) aH 7 aH and Th = Hay f= H+nZ 588,Given that: H = x(a) + bx) + xa(aq + baa) Then, after simplification, a“ 1a) + 2bix1 ~ (az + 2bax2) Combining these equations gives after reduction: Fi, =a, + bi tx2eibi—x2ba) and fh = a2 + baz x1 (ejb1 mba) These clearly are not the same as the suggested expressions, which are therefore not correct. Note. that application of the summability equation to the derived partial-property expressions reproduces the original equation for #7. Note further that differentiation of these same expressions yields results that satisfy the Gibbs/Duhem equation, Eq. (11.14), written: diy “e The suggested expresions do not obey this equation, further evidence that they cannot be valid. 11.15 Apply the following general equation of differential calculus: (3)-@)+@),@). ead al ed al Bm dram Ltr den, L OF doy KOM) 2m, (tM) (av aM) (av +057), Seen : "(F), Gee. By definition, MY) 2 ( o n() anor ( Peg aes Tnem . Inte Therefore, oy (aM fnew Pa) 11.20. Equation (11.55) demonstrates that [n 6, is a partial property with respect to G*/RT. Thus Indy G,/RT, The partial-property analogs of Eqs. (11.53) and (11.54) are: ae ‘i ainds AE RF = |r), ‘The summability and Gibbs/Duhem equations take on the following forms: ot ‘ 3 # ap Dvd and Dednd (const 7, >| 58911.26 For a pressure low enough that Z and In are given approximately by Bs. (3.37) and (11.35): BP BP Zal+e and ng= ap then Ing© 2-1 11.28 (a) Because Bq. (11.92) shows that In y is a partial property with respect to G#/RT, Egs, (11.15) and (11.16) may be written for M = G#/RT: GE adeG*sRT) GE dG*RT) y= gRte nn ap 7 ae Substitute xp = 1 —x1 in the given equaiton for G#/RT and reduce: 7 7 aGRT. ge 18x: +27 +082} whence sein 18425, + 24x? Thea, fing =—18+2m+14e7—16x7| and [inn =—x? 165 (8) In accord with Eq. (11.11), ap TA tale = C18 42m + 1.4x? = 1.653) + (1 —)(-2? - 1.623) Whence, Fe 18x) +47 +0.8x} ‘which isthe fist equation developed in part (a) (©) Write Bg, (11.14) fora binary system with diny | dinys Iny; and divide by dx): eCaanat uaal Differentiate the the boxed equations of part (a) ain, dinys > Te = 24+28x1—4.8xF and ae, 2x) — 48x} Multiply each derivative by the appropriate mole fraction and add: 21 +28.) 4.847) + = 21-21 = 4.8.47) ‘The validity of this equation is readily confirmed, (d) Substitute x1 = 1 in the first derivative expression of part (c) and substitute x; = 0 in the second derivative expression of part (c). The results ere:e 04 06 xy 11.29 Combine definitions of the activity coefficient and the fugacity coefficients: xP. & n Hie Note: See Eq. (14.54), 11.30 For C£ = const, the following equations are readily developed from those given ia the last cotueaa of Table 11.1 (page 404): = ‘Working equations are then HE-G a se and HE For Ty = 298.15, Tr = 328.15, (T) = 313.15 and AT = 30, results forall parts of the problem are given in the following table: HE +CBar and Gf = Hf ~ 1 SF W.For CE S$ uf oof GF oF Sf ok oF =622 1920 4354 42 109815951677 3.3 407-984 «1.935, -2.7 “sosi 1794 1974 | 4384 1020. 4914 1995 14oh 10399 Ler? 159510047 err (903 ‘3s28} 1935984348 @| 632 -208 -2817 23.0) -0.614 482 683.5) -2817 -208 716.5 (3 | 144s as “817 tol nt96 93818137 | "2817 40s isons | Ts 416 —3as7 t10|-2503 “85 ‘a339| "3057-6 ‘gua @| 759 1465 2.368 -8.0| 1.602 1225 699.5 2.368 1465 688.0 @ ® o 59111.31 (a) Multiply the given equation by m (=) + m2), and convert remaining mole fractions to ratios of ‘mole numbers: ee nt mom, 4 mits |, mans Be An A dy RT a n ” Differentiation with respect to m; in accord with Bq, (11.92) yields [(8n/11)u,.n) = U = Agm(1 ~ a1) + Aig 1) = Avex Similarly, Iny2 = Arr (1 = 23) — Aiea + dagen ~ 2) In yy = Ayana + Apsei (1 — a5) + Anvxa( — 3x3) (0) Bach In y; is multiplied by x,, and the terms are summed. Consider the first ‘erms om the right of ‘each expression for In ,. Multiplying each of these terms by the appropriate x, and adding gives: AaQs¥2 ~ x82 4X20) — x}ay — MaeaXs) = Anaxixa(1 1 + 1 — x2 — 3) = Apxiaal2 — (ty +2 +33)] = Aamir An analogous result is obtained for the second and third terms on the right, and adding them yields the given equation for G2/RT (©) For infinite ditution of species 1, InA@y = 0) = Arpxe + Arsxs ~ Apseexs For pure species 1, Inv =1) =0 For infinite ditution of species 2, In yes = 0) = Aisx? For infinite dilution of species 3, In yr(as = 9) = Aine} 11.38 By Eq. (11.84), written with M = G and with x replaced by y: G® =G¥ — S}yGF Equations (11.31) and (11.35) together give Gf = BjP. Then for a binary mixture: GF = BP ~ yBuP — yBnP or GF = P(B— yBu — Ba) Combine this equation with the last equation on Pg. 394: | G¥ = 812Pyyn ; Frome tcohamerTite 11 ageso: st = (82) 7 Because 5i2 is a function of T only: Priya Again from the last column of Table 11.1: CE (3) ‘This cquation and the preceding one lead directly to: 592on-Numerical Solutions Chapter 12 - Section B - AP 12eives: Pain Pt anh an dyn ) a PS (ao? -n Ben)e a (o?? n 12.2 Equation (12.1) may be written: yi? ‘Summing for / ap Differentiate at constant 7: = Py ( Apply this equation to the limiting conditions: dn For x; =0 m nayr wal an 4 For x1=1 = nay eo ayy ‘Thea, ap wtyoc_pet op = (SP (a),.-rr eG (Bt of (i) Sine both "and 7 are always positive definite, it follows that: nl pes 12.4 By Eqs. (12.15), Inn=ag and n= As? ‘Therefore, in 2! = AG} — af) = AG —x) = A280) ” A _yaPS (nln) (PM) _ a, By Eq. (12.1), BO ynP a GE) (Fs) ee ‘Whence, In(@j27) = ACL — 2x1) fan azeotrope exists, yz =1 at O is accompanied. by tas opposite extremum in In 72, Thus the difference ny; ~Iny2_ is also an extremum, and Bq. (12.8) becomes useful: : & iy — ny = nt = MORE pn de ‘Thus, given an expression for G°/RT = g(x), we locate an extremum through: @GYRT) _ dinn/n) det dx 593For the van Laar equation, write Bq. (12.16), omitting the primes (’): where As Anxy + dns Moreoves, and me dd Then eae a@(G°/RT) 2x, dd x as? a dx; 2andal eo xa 4 im (UA) ale te ad ran] 2Andn aA aA 24 (4 rntt) (nd 4 ‘This equation has a zero value if either 4); or 42) is zero. However, this makes G/RT everywhere zero, and no extremum is possible. If either quantity in parentheses is zero, substitution for 4 and dAjdx; reduces the expression to diz = 0 ot 42) = 0, again making G*) RT everywhere zero. We conclude that no values of the parameters exist that provide for an extrecaure iw bavi /9) ‘The Margules equation is given by Fq, (12.9b), here written: oe aa v4 Sean wl A= Ags, + An eee a rT where Aa + Ane Tay = A A ae aGF/RT) dA ‘Thea, “om Aan) braze #GYRT) da dA a4 OC = 24 or) S40 A py ax} lnm angy, tn a0 ge, hee da aa = 244g = 2] ry — xy dea — FE afer 2 4] ‘This equation has a zero value when the quantity in square brackets is zero. Then: aa oR (x2 ~ x1)(Aat — Ain) — Aaixt — Aiaea = Aavta + Avex 2A + AD) Substituting xp — x1 and solving for x1 yields: Ay = 2d 2 34a — Ai) ” *=36=H 59412.7 When r= 2, x1 =0, and the extrema in In y; and Iny oveur at the left edge of a diagram sucht as those of Fig, 12.9, For values ofr > 2, the extrema shift to the tight, ceacking a limiting value fe 1 =00 at x1 =1/3, For positive values of the parameters, in all of these cases dai > Ay2, and the intercepts of the In, curves at xy = 1 are larger than the intercepts of the In yy curves at x1 = 0. When y= 1/2, x = 1, and the extrema in In y; and In y» occur at the right edge of a diagram such as those of Fig. 12.9. For values of r < 1/2, the extrema shift to the left, reaching a limiting value for r = 0 at x1 = 2/3. For positive values of the parameters, in all of these cases day < uz. and the intercepts of the Iny1 curves at x1 = 0 are larger than the intercepts of the in ys curves at m= No extrema exist for values of r between 1/2 and 2. Equations (11.15) and (11.16) here become: GE dG*RT) GE dGFRT) lon= pte amd nya Be (@) For simplicity of notation, omit the primes that appear on the parameters in Eqs. (12.16) and (12.17), and write Eq. (12.16) as: oF ay pp = Ae aty + Aaa $F = Avene where Ansty +4: ze a aGFRT) ax, and tay, = rare D— Angry + Anis) = BEE dau, + Aix) Aux (42 + Ane)? D ‘Anita Anx inn = An(1 neta) ‘The equation for In yz is derived im analogous fashion. : ©) wnt To Pca, tan = [ACHAT su 2286 us et nF _ A == where aD = Ayn + Ayn RT 595Differentiation in accord with the first equation gives: a 1 _m_ (amp) 2g) = ota ‘The remainder ofthe derivation is the same as in Part (a). 12.16 This behavior requires positive deviations from Raoult’s law over part of the composition range and negative deviations over the remainder. Thus a plot of G* vs. x starts and ends with GE = 0 at x1 = Oand.x; = 1 and shows positive values over part of the composition range and negative values over the remainder, with an intermediate crossing of the x: axis, Because these deviations are usually ‘quite small, the vapor pressures P;*" and P," must not be too different, otherwise the dewpoint and bubblepoint curves cannot exhibit extrema. 1211 Assume the Margules equation, Eq. (12.9b), applies: e Ferd + Ann) — and Zequimola) = bain + An) em anda + Ann Fteauimolar) = Edin + Aa But [see page 424, just below Bq. (12.106): Ae ly? Any = ny & equimolar) = Hin y +t SF equimota = 1 SF tequimolan = Ftiny® sing) or |S equimotr HY) xX}(0.273 + 0.096 x1) + x2¥9(0.273 ~ 0.0962) ¥1x2(0.273.¥2 + 0.096.522 + 0.273 x1 — 0.096122) = x120.273)0) +2) Ge Fp tran (6) The preceding equation is of the form from which Eqs. (12.15) are derived. From these, Inn = 0.27383 and nye = 027337 (©) The equations of part (6) are not the reported expressions, which therefore cannot be correct. See Problem 11.11 12.28 Write Bg. (11.96) for a binary system, and divide through by «xy din din in dete 0 whence = AA __ dian _ din _ a dx, m2 dx; 2 dr 596 xIntegrate, recalling that In yp = 1 for x = 0: x dina if a dinyy in as a ae ae mdf de ym dx ™ : ann (@) For Inj, = Ax, Ot =24n Whence ny =2a [ nde or inna as By Eq. (12.6), (0) For Inyy = Whence nya 2A [mide +39 [nde 38 [xan I to I : alae b inp = ar} + 2xt— ax} or inna (44% an) =a [a4 04200] sane 3B Apply Bq. (12.6): & aad(d + Bx) + wax} + > ~ Bu) Algebraic reduction can lead to various forms of this equation; e.g, Ge B F oaafa Fara] (ec) For Inyy = x}(4 + Bxz + Cx3), PON ood + Beat Cx) +B +20n) =2Ae +3Bd 4d Ie = Dax; + 3Bxg(1 —m) +4001 — 4)? Whence ay 24 f eat +38 f Mal andny sac [sya I hb A or nye =Qd +3a+acy [ side, 08480) [stan tac [sax 5 fi A+ 3B +4C 3B+EC) yas ZY i> CEES) a vent Inys 3B mnasi[er Perc (ar 2) cu] 9977 wand [arfesais Gasm+%8]| ‘The result of application of Eq. (12.6) reduces to equations of various forms; e.g. o a c are [4 + pita) + Fd tat ap and AH = AH +A) 12.40 (a) As shown on page 444, x1 = oy Oe Eliminating 1 +7 gives: ane? my dan Ally ds, Differentiation yields: pote rare a where Whence, Combining this withthe result of Par () gives: FA = From which, i= 8H - anf Substitute: Py pie gage nate mH 598fxg Hea mfif Whence, pot’ Rye oe area AE fi However, by the summabilty equation, #7 — sf ‘Then, T= HE 12.41 Combine the given equation with Eq. (A) of the preceding problem: Sif = sais + Arve) With xp =1—x) and xy =1/U+A) (page 444): x ‘The preceding equations combine to give: ki-— (¢ +H (a) It follows immediately from the preceding equation that: tim AH = 0 (0) Because fi/(1 +i) + 1 for fi —> 00, it follows that: (©) Analogous to Eq. (12.10b), page 424, we write: Eliminate the mole fractions in favor of : 1 ji AE (=) [arta aot] In the limit as i? — 0, this reduces to Aa. From the result of Part (a) of the preceding problem, it follows that ast av dit Ant 12.42 By Eq, (12,29) with MF ) SH =H ~ Dix. Differentiate: (22),-@,-2@, With (¥) =Cp, this becomes (3) =Cp~ SisiCn = ACr ai Therefore, f aaH. i [lecea [ans ame fh acrar 599Chapter 13 - Section B - Non-Numerical Solutions 134 (@) ANH (@) + 502(g) + 4NO(g) + 6HLO(®) ee T B By Bq, (13.5), er ~5e 4e b= DMmy= FE, A= FE MOTE MMO=Zye ® 2HS(g) + 302(@) + 2H1:0(g) + 280218) By Eq. (135), : _ 2 _ 2 ste OO ere MORTEM BEE © 6NOn(g) + 8NHs(@) > TNo(e) + 12H20(2) ve Da -6- 84741255 m= P= 344H1=8 By Eq, (13.5), _ 3-60 4-86 _ 1446 12s wor ay5e OM BES. OM Bese HOT RE Se 132 Coal) + }Or(@) + ((CHs)2)1@) wo CaHg(g) + 302(g) > 2CO2(g) + 2H20(g) Q) ‘The stoichiometric numbers v,,, areas follows: By Eq. (13.7), Jet =133 CO2(g) + 3H2(g) + CH;OH(@) + H20(g) oO COz(g) + Hz) > COG) + H:0) Q ‘The stoichiometric numbers v,; sre as follows: Oz Hh CHOCO HO Bens oye ite 1 1-3 ai ° eee m= Sa2454128 ByEg.(13.7, ee & l+e Ste pete e gee HON Fe, POO Bde, MO SIDE, 13.7 The equation for AG*, appearing just above Eq, (13.18) is: an T ace T ACZaT AHS - = a — AG +R Pa? ~RT re AG IS ane fa fi z |, RT To calculate values of AG*, one combines this equation with Eqs. (4.19) and (13.19), and evaluates parameters. In each case the value of Aflj) — Afiigg is tabulated in the solution to Pb. 4.21, In addition, the values of 4.4, AB, AC, and AD are given in the solutions to Pb. 4.22. The required values of AG} = AGieg in J mol"! are: (a) -32,900; (/) ~2.919,124; (i) 113,245; (n) 173,100; (*) 39.630; (0) 79,455; (u) 166,365; (s) 39,430; (9) 83,010 13.8 The relation of K, to P and K is given by Eq. (13.28), which may be concisely written: o-()"s (@) Differentiate this equation with respect to T snd combine with Eq, (13.14): Ge),-G) ‘Substimute into the given equation for (86, /97) (b) The derivative of K,. with respect to P is: () (FY 601Bg ‘Substitute into the given equation for (3/3 P)r: (F), (© With Ky= F100", ky = Devin, Pilleremiation then yet: Ldky yy Ky dee Sy, de (A) dy Vide om dn de, nde. mde, Because yy = m/m, But nrg b Ube and n= My + vee Whenee, ‘Therefore, Substitution into Eq. (4) gives teas vw (aye Ede be (2) In this equation, both Ky and ng-+ vee (= n) ate positive. It remains to show thatthe summation term is positive, If m = 2, this term becomes f 8 o 4 ye, typ 2 mg toy = y » ya where the expression on the right is obtained by straight-forward algebraic manipulation. One can proceed by induction to find the general result, which is Dy ey? <2 vive All quantities in the sum are of course positive 3N2@) + jG) > NH) For the given reaction, v = —1, and for the given amounts of reactants, ng = 2. jase) By Eq. (13.5), Nk By Eq. (13.28),13.10 17 ay p > Whence, Goat 6) (3) Ka 1299 55 This may be written: red —2rep+(r—-1)=0 where, ‘The roots of the quadratic are: Because 6 <1, = 1—r-¥?, ‘The reactions are written: Mary: 2NH; + 3NO — 3H;0 + $Np 4) Paul: ANH: + 6NO > 61:0 + 5Nx @ Peter: 31,0 + §N; > 2NH, +3NO © Each applied Eqs. (13-116) and (13.25), here written: IK =-aGyRT ond K = (PY TCA" For reaction (4), AG = 3AG%,, ~ 28%, — 3G ig For Mary's reaction » = }, and A pn i sy! fueling and nk, = 294 FhusTia a For Paul's reaction v = I, and Shao Fin ~2A6% Ka=@Py! we and = InKe 4 Fius Sie oe For Peter's resetion » = —4, and Ko = (PY Mary: (pyPaul: Peter: ‘Taking the reciprocal yields Mary’s equation 13.24 Formation reactions: INo + Whe > Nis w @ ° Hy +40; + 120 ® Combine Eq, (3) with Eq, (1) and with Bq, (2) to eliminate Nz NO» + }H; > NH + 02 5) NO» > $0; +NO 6 Te set now comprises Eqs. (4), (5), and (6); combine Eq, (4) with Eg, (5) to eliminate Hy NOp + $10 NH +1302 o Equations (6) and (7) representa set of independent reactions for which r = 2. Other equivalent sets of two reactions may be obtained by different combination procedures. By the phase rule, Fa2-xtn- 2-145-2-0 wo (PY pie (a) Equation (13.28) here becomes: t.(<)K=K 13.35 (a) Equation (13.28) x (FB) Whence, =" Kcr) | (6) The preceding equation indicates thatthe equilibrium composition depends on temperature only. However, application of the phase rule, Eq. (13.36), yields Fo2+2-1- 2 This result means in general for single-reaction equilibrium between two species A and B that two degrees of freedom exist, and that pressure as well as temperature must be specified to fix the equilibrium state ofthe system. However, here, the specification that the gases are ideal removes the pressure dependence, which in the gencral case appears through the ds. 13.36 For the isomerization reaction in the gas phase at low pressure, assume ideal gases. Equation (13.28) then becomes: ye _ (2 y lay, -) K=K whence YA = KD) ma & mK 604Assume that vapor/liquid phase equilibrium can be represented by Raoult’s law, because of the low pressure and the similarity of the species: APD) =nP and (1 xa) PENT) = = ya) P (a) Application of Eq. (13.36) yields: (6) Given T, the reaction-equilibrivum equation allows solution for ya. The two phase-equilibrium ‘equations can then be solved for x, and P. The equilibrium state therefore depends solely on T- 13.38 (a) For low pressure and a temperature of 500 K, the system is assumed to be a mixture of ideal ‘gases, for which Eq. (13.28) is appropriate, Therefore, oa (B)'« aK (2) «= () Ku (@) These equation equations lead 0 the folowing set na Kivox | (1) [ox = Knox] (yen = Kinyox | @) ‘The mole fractions must sum to unity, and therefore; vox + Kiyox + Kuyox + Kmyox = Yox(1 + Ki + Ku + Kun) = 1 i Jox = TPE ET Kw ® (©) With the assumption that AC'z = 0 and therefore that Kz = 1, Eqs. (13.20), (13.21), and (13.22) combine to give: s = exp (—AGis8 aces) Altay (, _. Te K=KoK, ~e( Fe)? | ee (l- F 298.15 att (i= 28) — a Whence, (8.314) 298.15) K exp ‘The data provided lead to the following property changes of reaction and equilibrium constants at 500 K; Reaction | AHZq AGig K 1 | -1,750 2.8470 =1,040 ~1,000 1.2637 Mm | 10920 8690 0.1778 (@ Substitution of numerical values into Eqs. (1), (2), (3), and (4) yields the following values forthe mole fractions: vox = 0.1891 nox = 0.5383 Yox = 0.2390 rw = 0.0336 605Chapter 14 - Section B - Non-Numerical Solutions 14.2 Start with the equation immediately following Eq, (14.49), which can be modified slightly to read: s (nG"/RT inZ) ainz where the partial derivatives written here and in the following development without subscripts are understood to be at constant T', n/p (or p/n), and n,. Equation (6.59) after multiplication by n can be written: nck PY 32 ey Tar = 2mm) (2) + sntincy (2) —ninz Differentiate: a@GYRT) _ 42 ay.3 (Eee endo + 5 (E nG* fi 3 or BOC TED) a8 4.) + 39220 46) Inz Sn amBy cae Gm br The equation of state, Eq, (3.39), can be written: By definition, Zant Bo+C oe n2mnt nds (2) +02) (2) (nz) an; Differentiate + (2) entry + (2) ante +2 1+ p(B+B)+eQC+E)) When combined with the two underlined equations, the initial equation reduces to: Ing, 14 9B +B) + PAC +) ‘The two mixing rules are: 2By B=yiBy + 2iy2Bo C=C + SyfmCi2 + 3ryFCm + 2Cae Application ofthe definitions of Band C; to these mixing rues yields: 12 —yi)Br +29} Bu 2G = 2yndCin + 6y123Cu12 + 3y3(1 ~ 2y1)Ciza — By} Caz {Bir + 2yf Bia + y2t2 — ya) Bro 2yi Cin + 3¥FC1 — 2ydCii2 + 6y1¥3Cina + 2973 — 2y2)Cax2 60614.1 In combination with the mixing rutes, these give: B+ B, = 201 + Bu) 2C + Cy = 307Ciu + 2ymCra + 93Cin) B+ Bz = 2G2Bu + y1Bi2) 2C + Cy = 303Can2 + 2y192Ciza + Y7Ci2) In combination with the boxed equation these expressions long with Eq, (3.38) allow calculation of Indy and Inge, For the case described, Bgs. (14.1) and (14.2) combine to give: yy P = xP) If the vapor phase is assumed an ideal solution, 9; =), and yjP =x;P) When Eq, (3.37) is valid, the fugacity coefficient of pure species jis given by Eq, (11.38): — — BaP _ Ble PY For small values of the final term, this becomes approximately: of, umn — snp [i BEEP aT Write this equation for species 1 and 2 of a binary mixture, and sum. This yields on the left the difference between the actual pressure and the pressure given by Raoult’s law: P— Pony = HE Py esBals (Ppt = P) Because deviations from Raoult’s law are presumnably small, P on the right side may be replaced by its Raoul’s-law value. For the two terms, Pt P= PM 2PM Pt PS a2) PM — Pt = (PPS PS ~ P= PS PM PM = PS PM x) PA = (PS Be) Combine the three preceding equations ut Br (PM — PPM xx RT eae (Bo — Bes pt = psy (Bn Pi ~ BaP) 607Rearrangement yields the following: snp Pe — PE)? (By BY — Bea PM P—PIRL) = ane es (aoe) RT PS — PF xn(Pet ~ PS [oy + ~ Bu) PS 7) 7A | Clearly, when Bz: = Brs, the term in square brackets equals 1, and the pressure deviation from the Raoult’s-law value has the sign of Bi; this is normally negative. When the virial coefficients are not ‘equal, a reasonable assumption is that species 2, taken here as the “heavier” species (the one with the smaller vapor pressure) has the more negative second virial coefficient. This has the effect of ‘making the quantity in parentheses negative and the quantity in square brackets < 1. However, if this latter quantity remains positive (the most likely case) the sign of By, still determines the sign of the deviations. 14.13 By Eq. (11.87), the definition of, Iny, = In fy ~ Inxy ~ Inf wens Ta ayaa ‘Combination of this expression with Eq. (14.67) yields: jas” 0 pecawse za, | 2450 coos. r) By Eq. (11.42), the definition of fi, = Combination with Eq. (14.68) yields: 14.14 Stability requires that AG <0 (see Pg. 556). The limiting case obtains when AG = 0, in which event Eq, (12.30) becomes: oF aT Dx inxy Foran equimolar solution x; = 1/N where Nis the number of species. Therefore, GF (max eel 1 a atat <= InN = RT InN RTS in gy = AT Ey WN = aT and GF (max) = RT In2 For the special case of a binary solution, N 60814.17 M19 1421 14.23 According to Pb.11.38, G&=8,2Pyy2 or Ge This equation has the form: S— = Axx his equation has RF for which itis shown in Examples 14.5 and 14.6 that phase-splitting occurs for 4 > 2. Thus, the formation of two immiscible vapor phases requires: 12P/RT > 2. Suppose 7 = 300 K and P = 5 bar. The preceding condition then requires: 612 > 9977 em? mol! for vapor-phase immiscibility. Such lange positive values for 8:2 are unknown for real mixtures. (Examples of gas/gas equilibria are known, but at conditions outside the range of applicability of the two-term virial EOS.) GF Consider a guadratic mixture, deseribed by: =. = Axyep It is shown in Example 14.5 that phase splitting occurs for such @ mixture if A > 2; the value of A = 2 corresponds to a consolute point, at x: = x2 = 0.5. Thus, for a quadratic mixture, phase-spliting obtains i of oat tL eraosar This is @ model-dependent result. Many liquid mixtures are known which are stable as single phases, eventhough G¥ > 0.SRT for equimolar composition. ‘Comparison of the Wilson equation, Eq, (12.18) with the modified Wilson equation shows that GRD )m = C(GE/RT), where subscript m distinguishes the modified Wilson equation from the original Wilson equation, To simplify, define g@ = (G4/RT);, then Bm = CE gm = Cg. Inn = Clay, where the final equality follows from Bq, (11.92). Addition and subtraction of Inx; on the left side of this equation and of C In; on the right side yields ln(siyie = ney = CIn(eyy) — Clan, or In@eiyi)n = C Inger) — (C= Nina : dingayn _ dine - Differentiate: a > eee As shown in Example 14.7, the derivative on the right side of this equation is always positive. How- ever, for C sufficiently greater than unity, the contribution of the second term on the right ean make dingy dx, over part of the composition range, thus violating the stability condition of Bq, (14.67) and implying the formation of two liquid phases, <0 @ Refer to the stability requirement of Eq. (14.66). For instability, ie., for the formation of two Tiguid phases, @UGE RT) 1 dd = 60914.29 1430 1431 over part of the composition range. The second derivative of G® must be suliciently negative so as to satisfy this condition for some range of x). Negetive curvature is the norm for mixtures for which G* is positive; see, eg., the sketches of G* vs, x; for systems (a), (2), (), (e), and (f) in Fig. 11.4. Such systems are candidates for liquid/liquid phase splitting, although it does not in fact occur for the cases shown. Rather large values of G* are usually required, (b) Nothing in principle precludes phase-splitting in mixtures for which G* < 0; one merely requires that the curvature be sufficiently negative over part of the composition range. However, positive curvature is the norm for such mixtures. We know of no examples of liquid/liquid phase- splitting in systems exhibiting negative deviations from ideal-solution behavior. The analogy is Raouit’s law, Eq. (10.1), applied at constant P (see Fig. 10.12): ypP = 11, Ifthe vapor phase in VLE is ideal and the liquid molar volumes are negligible (assumptions inherent in Raoult’s law), then the Clausius/Clapeyron equation applies (see Ex. 6.5) dine _ Ani @ R Integration from the boiling temperature T, at pressure P (where P,** = P) to the actual temperature T (where PB = P,** gives: Combination with Bq, (10.1) yields: which is an analog of the Case SLE equations. Consider binary (to-species) equilibrium between two phases of the same kind. Equation (14.70) applies: xtytaafyf = 1,2) Irphase pis pure species 1 and phase is pure species 2, then xf = yf =1 and xf md oyfaahyP=t Henee, atyt =afyt = ‘The reasoning applies generally to (degenerate) N-phase equilibrium involving ’ mutually immiscible species. Whence the cited result for solids. The rules of thumb are based on Case II binary SLE behavior. For concreteness, lt the solid be pure species ! and the solvent be liquid species 2. Then Eqs. (14.89) and (14.88a) apply: ) AH?! n= vsey Sl ( ax AH (a) Differentiate: Spa Sp Thus dxi/d7 is necessarily positive: the solid solubility x; increases with increasing 7. (6) Equation (14.88a) contains no information about species 2. Thus, to the extent that Eqs. (14.89) and (14.88) are valid, the solid solubility x is independent ofthe identity of species 2. 610(c) Denote the two solid phases by subscripts 4 and B. Then, by Eqs. (14.89) and (14,88a), the solubilities x4 and xp are related by: XA gp | SH Tins = Ta) facet Tas Pa ‘where by assumption, An] = Hj = ant Accordingly, x4/xp > 1 ifand only if Ty 7 (See Fig. 14.21b). Then x4/tq > 1 ifandonlyif AH < SHG, in accord with the rule of thumb. 14.34 The shape of the solubility curve is characterized in part by the behavior of the derivative dy, /4P (constant 7). A general expression is found from Eq. (14.94), »; = PSP /Fi, where the enhance- ment factor F; depends (at constant T) on P and y;. Thus, #(),-@)2| “BenQ, C59) 3] in (4), 1 ] ap (ain Ae a ay This is a general result. An expression for Fis given by Eq, (14.95) pat Whence, oe PP) exp A RF From this, after some reduction: in Fi) aindy WE (Ch }, -() Rr ( Whence, by Eq. (4), (8)‘This too is a general result. If the two-term virial equation in pressure applics, then Ing, is given by Eg, (11.59), from which: ands 1 aindy 2yabi2P (0B!) = frases we (ORB) = Vix Bu - yu _ 1 dy af RT P SaP RT Whence, by Eq. (B), The denominator of this equation is positive at any pressure level for which Eq. (3.37) is likely to be valid. Hence, the sign of dy, /d P is determined by the sign of the group in parentheses. For very low pressures the 1/P term dominates and dvi /dP is negative. For very high pressures, 1/P is small, and dy;/aP can be positive. If this is the case, then dy /dP is zero for some intermediate pressure, and the solubility yy exhibits a minimum with respect to pressure. Qualitatively, these features are conisistent with the behavior illustrated by Fig. 14.22. However, the two-term virial equation is only valid for low to moderate pressures, and is unable to mimic the change in curvature and “fattening” of the »; vs. P curve observed for high pressures for the naphthalene/CO; system, 14,35 (a) Rewrite the UNILAN equation: =F inie+ Pet) info + Pe] Ca As s+ 0, this expression becomes indeterminate. Application of PHépita’s rule give imn = tim™ (Pe Pew sa" = 807 oe Pet” oF Pee =4( ae “ TNCEP eH or Which is the Langznuir isotherm, () Henry's constant, by definition: — = fim jeury’s constant, by definition; = fim SE dn_m(e e Ditferentiate Eq. (a): “(8 ce a 5 (cine er Pe Whence, 2465) « (©) All derivatives of n with respect to P are well-behaved in the zero-pressure limit: m ™ sinh s dn fim = Zosinhs 61214.36 1437 Bee. Numerical studies show that the UNILAN equation, although providing excellent overall correlation of adsorption data at low-to-moderate surface coverage, tends to underestimate Henry's constant Start with Eq. (14.105), written as: ingP/m) =—ink + f'@— 2-1 With 2=148n+Cn?-+--, this becomes: In(P/n) = ~Ink +2Bn + det + Thus a plot of In(P/n) vs. m produces —Ink as the intercept and 2B as the limiting slope (for n> 0), Altemstively, a polynomial curve fit of In(P/m) inm yields —Ink and 2B as the frst two coefficients For species i in a real-gas mixture, Eqs. (11.42) and (11.48) give: bh = UD) + RT inyidyP RT dinydP At constant temperature, aut With dy, uf Eq, (14.101) then becomes: Feat dln + Yxdinysds = 0 (const 7) For pure-gas adsorption, this simplifies to: a fan= (cons FpaadinP+ding (const 7) ey which is the real-gas anslog of Eq. (14,103). On the left side of Eq, (4), introduce the adsorbate compressibility factor through = =: Ta/RT = I14/nRT: a dn gpa a de (8) where n is moles adsorbed. On the right side of Eq. (4), make the substitution: ap ding=@- D> © which follows from Eq. (11.34). Combination of Eqs. (4), (B), and (C) gives on rearrangement (see See. 14.8) ne dn dP ding = 0-9 dee ZS which yields on integration and rearrangement: vairen fe -y'2-o9[ fa This equation is the real-gas analog of Eq, (14.105). 61314,39 & 14.40 Start with Bq. (14.105). With z= (1 —bm)-', one obtains the isotherm: n= EPC — br)exp (- w bn For bn sufficiently small, exp (>) a1 kp Whence, by Bq. (4), © EP(L~ 2bm) eon tee eee T+ 35kP which isthe Langmuir isotherm With 2= 1+ Bn, the adsorption isotherm is: KP exp(—2Bn) from which, for Bn sufficiently small, the Langmuir isotherm is again recovered Adm dP 1441 By Fa, (14.103) with a= A/m, S6H- SE yg, (14.108) with @ = dfn, SEP a WZ The definition of y and its derivative ar: aan and ai Whence, wo @) By general differentiation, » ” n= Hey © ay Pav pet Lge? © The equation, ¥;x; = 1, is an approximation that becomes increasingly accurate asthe solution procedure converges. Thus, by rearrangement of Fg, (B), pe LF, With P fixed, Eq. (C) can now be written in the simple but approximate form: aP @Du=5 Buss Equation (4) then becomes: dyandDx or sy =na( Ex) ‘where we have replaced differentials by deviations. The deviation in J°, x is known, since the true value must be unity, Therefore, i bDn =P -1 ae 61a14.42 1 Leusnsy By Eq, (14.128), Combine the three preceding equations yi PY ae iy = ST _ YS ei/n) P/PS, the Raoult’s law anslogy, is substituted the required equation is reproduced: bye "ee Multiply the given equation for G#/RT by n and convert all mole fractions to mole numbers: ay a ‘Apply Eq. (11.92) for # 1) pam) a tny, = diom (= 22) 4 dim ($= 8) — antat = Ajaa(l — 4) + Ars = x1) = Aaysnxs Introduce solute-free mole fractions: % wd xe te * ‘Whence, day = Aor} — x1)? + Araxs) — x1)? — Ansxdx$ (1 — x1)? Fors 0, ln yf? = Anaes + Aisxs — Aasxixh Apply this equation to the special case of species 1 infinitely dilute in pure solvent 2. In this case, xsl, xh=0, and my = Ai Also Iny = Ais Whence, In yp? = xh 723 4 x5 In yf — Aasxtas |In logarithmic form the equation immediately following Eq, (14.24) on page 536 may be applied to the several infinite-dilution cases: In =n fitiny® — Ay a=InFitiny twas nf +iny?s ‘Whence, In Ay = In fy = x4 (ln Hy 2 — In fi) + 44m Hy 3 — In ft) — Arsxixh or In yin Mia + x4 InAs — Aastix) 61s14.43 For the situation described, Figure 14.11 would have neo regions like the one shown from « to f. probably one on either side of the minimum in curve I. ty aT 1444 By Eq. (14.123) with Py = Vp Incr) Represent in y» by a Taylor series: tnralnno + 222] a ny eines me] ate But at x; = 0 (x2 = 1), both In y and its first derivative are zero. Therefore, 1 (any i ‘ if at di i Also, Ingy Ind =) =x) - 1/@inyg 13 ast ye 1 1 (@loyy at p aa ( as ) od: * Iny Therefore, In(xzy3) = +Inx2 + In» and. B 616Chapter 16 - Section B - Non umerical Solutions 16.1 The potential is displayed as follows. Note that K is used in place of & as a parameter to avoid confusion with Boltzmann’s constant. ‘Combination of the potential with Eq, (16.10) yields on piecewise integration the following expression for B 2 B= aN [4K =H ey PREM 1) BBN og yee tT 4 Reeth From this expression, SF = £5 [-(A? ~ nge¥7 4 (P — K*yee"7] according to which dB/d7 —0 for 7» co and also for an intermediate temperature Ty e+e ol Ge)| ‘That Tr, corresponds to a maximum is readily shown by examination of the second derivative d*B /dT?, 16.2 The table is shown below. Here, contributions to 2 (long range) ate found from Eq, (16.3) [for U(et)}, Bq, (16.4) [for Mind], and Bq, (16.5) [for (disp)}. Note the following: 1, As also seen in Table 16.2, the magnitude of the dispersion interaction in all cases is substantial 2. U(el), henec fe!), is identically zero unless both species in a molecular pair have non-zero permanent dipole moments, 3. As seen for several of the examples, the fractional contribution of induction forces ean be substantial for unlike molecular pairs. Roughly: (ind) is larger, the greater the difference in polarity of the interacting species. 617Molecular Pair = Cg/10- Jm® fel) find) f(disp) fed F(disp) CHUCHH ig 498 oo 1000 0 CHyYCHCh 343 0 0,008 0.992 a CHa(CHs).CO 249 0 0088 0.912 8 CHYUCH,CN 2.1 0 0188 0812 ° GHeCHCh 161.9 0 0008 0.992 0 CHHye(CHS):CO 119.1 0 0096 0.904 8 CHyg/CH3CN 106.1 0 0.205 0.795 0 CHCly/(CH3)2CO 95.0 0.143 0.087 0.770 0.186 CHC1;/CH3CN. 983 0.263 0.151 0,586 0.450 (CH)COICHSCN 27030805. 0.052 0.142——5.680 16.3, Water (#,0), a highly polar hydrogen donor and acceptor, is the common species forall four systems; in all four cases, it experiences strong attractive interactions with the second species. Here, interactions between unlike molecular pairs are stronger then interactions between pairs of molecules of the same kind, and therefore A is negative. (Sec the discussion of signs for H in Sec. 16.7.) 16.4 Of the eight potential combinations of signs, two are forbidden by Eq. (16.25). Suppose that H® is negative and $® is positive, Then, by Eq. (16.25), G* must be negative: the sign combination G¥ @, H® 9, and S® @ is outlawed, Similar reasoning shows that the combination G® ©, H® @, and S© © is inconsistent with Eq. (16.25). All other combinations are possible in principle. 16.5 In Series A, hydrogen bonding occurs between the donor hydrogens of CHCl: and the electron-rich benzene molecule. In series B, a charge-transfer complex ocours between acetone and the aromatic benzene molecule. Neither cyclohexane nor n-hexane offers the opportunity for these special salvation interactions, Hence the mixtures containing benzene have more negative (smaller positive) values of H® than those containing cyclohexane and n-hexane. (See Secs. 16.5 and 16.6.) 16.6 (a) Acetone/eyclohexane is an NAINP systeon; one expects G¥ ®, H® ©, and S® &. (®) Acetoneidichloromethane is a solveting NA/NA mixture. Here, without question, one will see GF 6, H® 2, and S¥ 8, (©) Aniline/eyctohexane is an AS/NP mixture. Here, we expect either Region I or Region II behavior: GF @ and H® ©, with SF @ or. [At 323 K (50°C), experiment shows that S® is @ for this system] (A) Benzene/carbon disulfide is an NP/NP system, We therefore expect G* &, H® ©, and S* @, (©) Benzenetn-hexane is NP/NP. Hence, G* @, H® ©, and S® @. (A) Chloroform/i,4-dioxane is a solvating NA/NA mixture. Hence, G® ©, H® ©, and S® ©. (2) Chloroforin/a-hexane is NA/NP. Hence, G® @, H® @, and S* ©, (A) Bthanol/n-nonane is an AS/NP mixture, and ethanol is a very strong associator. Hence, we expect Region Il behavior: G* @, H® ®, and S® 6. 16,7 By definition, 2[By —$(6u+By)] At normal temperature levels, intermolecular attractions prevail and the second vial oeticents are negative. (See Sec. 16.2 for a discussion of the connection between intermolecular forces and the second virial coefficient) ITinterations between unlike molecvar pairs are weaker than interactions between pairs of molecules of the same kind, Byl < HB + By| 618and hence (since each B is negative) 4; > 0. Ifunlike interactions are stronger than like interactions, [Byl > HB + Byl and hence 6 <0. [interactions are identical for all molecular pairs, By = Bu = By and by =0 ‘The rationalizations of signs for H of binary liquid mixtures presented in See. 16.7 apply approxi mately tothe signs of 2 for binary gas mixtures, Thus, postive isthe norm for NP/NP, NAJNP, and ASINP mixtures, whereas diz is usually negative for NA/NA mixtures comprising solvating species One expects 612 to be essentially zero for ideal solutions of real gases, e.g, for binary gas mixtures of the isomeric xylenes 619

Solution Manual Chemical Engine PDF

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Solution Manual Chemical Engine PDF

Uploaded by

Copyright:

Available Formats

You might also like