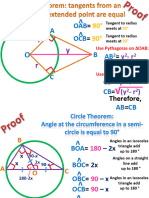
Solution for Problem 4

∴∆FGD is an equilateral triangle.

Connect AC
∴ FDG = 600
As given that DA=DC,  DAC = DCA=β
Since DFB = 900
Now connect BD
FBD = 300
Draw the angular bisector of BCD, say it
meets BD at G, and draw a perpendicular to In triangle GCB,
AB from D, say it meets AB at F.
GBC = 900 - α
Since ∆BDC is isosceles, angular bisector of
BCD, bisects the Base BD and as well as Since ABC = ABD + CBD
perpendicular to it. ABC=300 + 900 - α
Therefore DG=BG i.e.: ABC=120 - α
Consider ∆FAD and ∆DGC
∴ x = 120 - α
FAD = GCD (both are α in magnitude)

AFD = CGD (both are 900)

AD = CD (Given)

So ∆FAD ≡ ∆DGC (Under A.A.S case)

∴FD = GD

Now draw a circle having its center at G and

its radius GD. It passes through D,F,B,
because GD=GB and DFB=900.

∴GF is another radius.

So, GF=GD=FD