THERMODYNAMICS

Briefly, the second law of thermodynamics states that heat

naturally flows from hot to cold, or equivalently, it states that
you cannot convert all of heat to mechanical work. I explained
how these two statements are equivalent in the class.
One important result is that, in the most efficient heat engine,
the heat transfers have to take place isothermally; this was the
Carnot engine working on the Carnot cycle. There are two other
cycles having the same efficiency as the Carnot cycle we have
seen in the class: Stirling cycle and Ericsson cycle. I
explained how Carnot efficiency is obtained in these cycles using
internal heat transfer between system components, called
regeneration.
None of the engines based on these cycles is practical (they are
efficient but give so little specific work that they can barely
overcome their internal friction), and only the Stirling cycle
has seen limited applications. They mostly serve as models that
we imitate in real life cycles so that we may increase
efficiency.
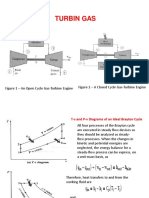
Then we saw Brayton cycle which is the basic one used in gas
turbine power plants and jet propulsion.
These idealized power cycles working on gas (air) are called air-
standard power cycles.
In Brayton cycle, heat transfer is at constant pressure, not
isothermal, therefore its efficiency is lower than that of
Carnot. So people naturally looked for ways to improve
efficiency, knowing of course that the efficiency, even
theoretically, cannot surpass Carnot efficiency.
One way to do this is called regeneration (or recuperation); we
have seen this term before. It refers to using hot gases within
the plant to heat cold gases at another location within the
system using heat exchangers.
In an actual plant, the heat exchanger at the top (where Q L is
given out-rejected) does not exist; the exhaust gases go out and
fresh air is taken into the compressor. But from thermodynamic
point of view, there is a heat exchanger.
Looking at the figure, the hot gases at the turbine exhaust are
used to heat cold gases at the entrance to the combustion chamber
(where heat transfer from outside Q H occurs). Of course, for
this to work, exhaust gases must be hotter, i.e., T 4 >T 2 in the
cycle. Otherwise no regeneration is possible.
(Thermal) efficiency
qL T −T 1
η=1− =1− A
qH T 3−T B
I remind you again that we always assume ideal gas with constant
specific heats (unless otherwise stated); and if the mass flow
rate in the cycle is ṁ , Q= ṁq and ṁ’s cancel.
The heat exchange within the regenerator does not come in here
because it is not an exchange with the surroundings (as was the
case in Stirling and Ericsson cycles).
For ideal regenerator
T B=T 4 , T A=T 2
i.e., all possible heat flow between the hot and cold gases
occurs. For example, the temperature of the hot gases decreases
to as low as the temperature of the cold gases entering the
regenerator.
This, of course is not possible. Actual points will be at T A '
and T B ' in the cycle. For the non-ideal, actual regenerator,
define regenerator efficiency as
h B ' −h2 h4 −h A '
ηreg = =
h B−h2 h4 −h A
(think why these are equal). You can replace h with T since
c p is constant.
Example.
Ideal Brayton cycle. Air k =1.4 . Temperatures T 1=21.1℃ ,
p2
T 3=982.2 ℃. Pressure ratio =8. Compute the efficiency for the
p1
following cases: no regeneration, with an ideal regenerator, and
with 70 % regenerator efficiency.
Ideal cycle, as we have seen before corona,
1
η=1− k−1
=0.448
p2
( )
p1
k

The case with ideal regenerator, T B=T 4 , T A=T 2 ,

T 2−T 1
η=1−
T 3 −T 4
k−1
p2
T 2=T 1
( )
p1
k
=533 K

T3
T 4= k−1
=693 K
p2
( )
p1
k

η=0.575
(increased).
Real regenerator with 70 % efficiency,

T A ' =T 4−ηreg ( T 4 −T 2 ) =307 ℃

T B ' =T 2+ ηreg ( T 4 −T 2 ) =372℃

T A −T 1
'

η=1− =0.468
T 3−T B '

(increased but not as much).

Another method to increase efficiency is intercooling (in the

compressor) and reheating (in the turbine). Below is a plant
with intercooling, reheating and regeneration:
(Note that this one is open to air, there is no difference as I
said).
The reason this one is more efficient is that compression and
expansion processes (zig-zags at the bottom and top) imitate the
constant temperature (isothermal) compression and expansion in
the Ericsson cycle, i.e., we are trying to approximate the
Ericsson cycle.
Think about how the T-S diagram is drawn.
Of course all these modifications to increase efficiency
increases cost.