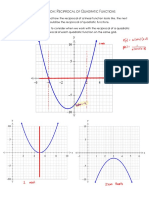
Q.2 (b) Explain Vertical line test and Horizontal line test.

Vertical Line Test:

The vertical line test is a graphical method of determining whether a curve in the plane represents
the graph of a function by visually examining the number of intersections of the curve with vertical lines.
The motivation for the vertical line test is as follows: A relation   is a function precisely when each
element   is matched to at most one value   and, as a result, any vertical line in the plane can
intersect the graph of a function at most once. Therefore, the vertical line test concludes that a curve in
the plane represents the graph of a function if and only if no vertical line intersects it more than once.
A plane curve which doesn't represent the graph of a function is sometimes said to have failed the vertical
line test.

The figure above shows two curves in the plane. The leftmost curve fails the vertical line test due to the
fact that the single vertical line drawn intersects the curve in two points. On the other hand, the vertical
line test shows that the rightmost curve is a function on its domain: Indeed, none of the vertical lines
drawn intersect the curve in more than one point and, by observation, neither would any other vertical
line.

horizontal line test:

Similar to the vertical line test, we also have a horizontal line test.
If we have a function, we can use the horizontal line test to tell if the function is one-to-one. One-to-one
means that for every specific input, the function has a specific output. This also means the
function's inverse is also a function.
The process is the same as the vertical line test. We draw horizontal lines and see how many places they
intersect our graph. If its at, at most, one point, then our function is one-to-one and we know its inverse is
a function.
One-to-one Function
Suppose we want to know if the following function is one-to-one:f(x)=(x+1)3−2First, we graph the
function. This is a cubic function.
 Made using Desmos
Then, we draw some horizontal lines through it and see where they intersect.
 Made using Desmos
Each of our lines only intersect the graph at, at most, one point. Therefore, we know this function is one-
to-one.
This means the function's inverse is also a function. Let's find the inverse and see.
To find the inverse, we swap the x and y variables
and solve for y again.y=(x+1)3−2x=(y+1)3−2x+2=(y+1)33√x+2=y+13√x+2−1=y
Here is our inverse function. If we graph this and apply the vertical line test, we will see it passes and is a
function.
To get to this inverse function, you may want to review the Addition and Subtraction Property of
Equality, the Multiplication and Division Property of Equality, cube roots,
 The inverse  y=3√x+2−1  passes the vertical line test so it's a function.
Made using Desmos
Not a One-to-one Function
Let's look at an example that doesn't pass the horizontal line test.f(x)=x2−1
Start by graphing the function.
 Made using Desmos
Next, draw horizontal lines through it.
 Made using Desmos
While one of our horizontal lines goes through only one point, the others we draw will go through two.
This means our function is not one-to-one. Our function fails the horizontal line test.
If we graph its inverse, it will not be a function and won't pass the vertical line test.
Let's take a look. Again, we swap the x and y variables and solve
for y.y=x2−1x=y2−1x+1=y2±√x+1=y
 The inverse  y=±√x+1 doesn't pass the vertical line test so it's not a function.
Made using Desmos
Even this graph isn't a function, it is still a relation!
Q.2 (c) Explain Horizontal and Vertical asymptotes.
An asymptote is a line or curve to which a function's graph
draws closer without touching it. Functions cannot cross
a vertical asymptote, and they usually
approach horizontal asymptotes in their end behavior (i.e.
as x→±∞x→±∞).
Looking at the graph of f(x)=x+2(x−1)(x+3)f(x)=x+2(x−1)
(x+3), you will notice that it has two vertical asymptotes (the
vertical dotted lines), one is at x=1x=1 and the other is
at x=−3x=−3.

Finding a Vertical Asymptote

We can find vertical asymptotes by simply equating the
denominator to zero and then solving for xx. In other words, if
f(x)=P(x)Q(x)f(x)=P(x)Q(x)
Then setting Q(x)=0Q(x)=0, will give the vertical
asymptote(s).
So if
f(x)=x+2(x−1)(x+3)f(x)=x+2(x−1)(x+3)
setting
(x−1)(x+3)=0(x−1)(x+3)=0
gives the vertical asymptotes at x=1x=1 and x=−3x=−3.
Finding a Horizontal Asymptote
Put the rational function in a standard form. That is, expand
the numerator and denominator if they are written in a
factored form.
Remove all terms except the terms that contain the
largest exponents of xx in the numerator and the
denominator.
There are three possibilities:
 If the degree of the numerator is smaller than the degree
of the denominator, then the horizontal asymptote crosses
the y−y−axis at y=0y=0. That is, it is the x−x−axis itself.
 If the degree of the denominator and the numerator are
the same, then the horizontal asymptote equals to the ratio
of the leading coefficients.
 If the degree of the numerator is larger than the degree
of the denominator, then there is no horizontal asymptote.