Professional Documents
Culture Documents
PDF 2 Law of Thermo
PDF 2 Law of Thermo
Uploaded by
maaz ahmad0 ratings0% found this document useful (0 votes)
10 views17 pages(1) The document discusses moving boundary work, which is the mechanical work done by the expansion or compression of a gas in a piston-cylinder device, such as in automobile engines. (2) It explains that the differential work done during a quasi-equilibrium process is the product of the absolute pressure P and the change in volume dV. (3) The total work done is calculated by integrating all differential work from the initial to final states using the pressure-volume relationship P=f(V).
Original Description:
Original Title
PDF 2 LAW OF THERMO
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Document(1) The document discusses moving boundary work, which is the mechanical work done by the expansion or compression of a gas in a piston-cylinder device, such as in automobile engines. (2) It explains that the differential work done during a quasi-equilibrium process is the product of the absolute pressure P and the change in volume dV. (3) The total work done is calculated by integrating all differential work from the initial to final states using the pressure-volume relationship P=f(V).
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
10 views17 pagesPDF 2 Law of Thermo
PDF 2 Law of Thermo
Uploaded by
maaz ahmad(1) The document discusses moving boundary work, which is the mechanical work done by the expansion or compression of a gas in a piston-cylinder device, such as in automobile engines. (2) It explains that the differential work done during a quasi-equilibrium process is the product of the absolute pressure P and the change in volume dV. (3) The total work done is calculated by integrating all differential work from the initial to final states using the pressure-volume relationship P=f(V).
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 17
Aerospace Thermodynamics
AS2007
Dr Surendra Ghadai
FIRST LAW OF THERMODYNAMICS
Moving Boundary Work
• One form of mechanical work mostly encountered in practice involved with the
expansion or compression of a gas in a piston-cylinder device
• Primary form of work in Automobile engines (Internal combustion engines)
• The piston moves back and forth
• Therefore, called as Moving boundary work or simply, boundary work
• How this work can be determined?
• Thermodynamics analysis?
• Very fast process – difficult to trace the equilibrium states and the path
it followed
• By measurement – Indicator diagram
• Whereas, for a quasi-equilibrium process, this displacement
work can be obtained
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work (quasi-equilibrium process)
• Consider the gas is enclosed in the piston-cylinder device
• Initial Pressure is P, and total Volume of gas is V and The
surface area of piston is A
• If the piston allowed to move a distance ds in quasi-equilibrium
manner, the differential work done will be
• So, the differential work is the product of absolute pressure P
and the change in volume dV
• Therefore, the moving boundary work is sometimes called the
P dV work
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work
• Now, P is absolute pressure, which is always positive
• dV is the differential volume, which is positive during an expansion process
(as volume increases) and negative during a compression process (as
volume decreases)
• Therefore, the differential work is positive for an expansion process (Work
output) and negative for a compression process (work input)
• The total boundary work done during the entire process is obtained by
adding all the differential work starting from the initial state to the final
state
• This integral can be evaluated, if we know the functional
relationship between P and V during the process i.e. P = f (V)
should be known.
• This P = f (V) is the equation of process path on a P-V diagram
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work
• The quasi-equilibrium expansion process shown in P–V diagram
• Differential area dA = P dV
•
• It reveals that the area under the process curve
on a P-V diagram is equal, in magnitude,
to the work done during a quasi-equilibrium
expansion or compression process of a closed
system.
• (On the P-v diagram, it represents the boundary
work done per unit mass.)
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work
• A gas can follow several different paths as it expands
from state 1 to state 2
• As the area under each path is different, the work
done will be different for each process
If work were not a path
function, no cyclic devices
(car engines, power plant)
could operate as power or
work-producing devices.
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work for Constant Volume process
• Since rigid tank has constant volume
• So, dV = 0. Hence, Wb = 0.
• Therefore, the boundary work done
during a constant volume process is
always zero.
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work for Constant Pressure process
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work for Isothermal process
• For an ideal gas at constant temperature T0,
• As
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work for Polytropic process
• For actual compression and expansion processes
of gases, the pressure and volume are often related
by
• This type of process is called as Polytropic process
• Work done for such process can be estimated from
•
• ,
• For an ideal gas , this equation can be written as-
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Moving Boundary Work
8/13/2021 KIIT Deemed to be University Dr Surendra Ghadai
Example 1
2
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Example 2
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
Example 3
8/12/2021 KIIT Deemed to be University Dr Surendra Ghadai
8/13/2021 KIIT Deemed to be University Dr Surendra Ghadai
Example 4
8/13/2021 KIIT Deemed to be University Dr Surendra Ghadai
Example 5
8/13/2021 KIIT Deemed to be University Dr Surendra Ghadai
You might also like
- HVAC - The Ultimate Guide To HVAC and Its ComponentsDocument29 pagesHVAC - The Ultimate Guide To HVAC and Its ComponentsGenesHeatingandAir100% (2)
- Practical Guides to Testing and Commissioning of Mechanical, Electrical and Plumbing (Mep) InstallationsFrom EverandPractical Guides to Testing and Commissioning of Mechanical, Electrical and Plumbing (Mep) InstallationsRating: 3.5 out of 5 stars3.5/5 (3)
- Southern Marine Engineering Desk Reference: Second Edition Volume IFrom EverandSouthern Marine Engineering Desk Reference: Second Edition Volume INo ratings yet
- CAPE Physics I1 P2 2019 SolutionsDocument4 pagesCAPE Physics I1 P2 2019 SolutionsLeah Cassie75% (4)
- Rig HydraulicsDocument60 pagesRig HydraulicsAbhinav Goyal100% (4)
- Career Change From Real Estate to Oil and Gas ProjectsFrom EverandCareer Change From Real Estate to Oil and Gas ProjectsRating: 5 out of 5 stars5/5 (1)
- LH265E-S6F-30.2 R404A t0 - 28 Tamb 32Document6 pagesLH265E-S6F-30.2 R404A t0 - 28 Tamb 32Gosai MohamedNo ratings yet
- A Guide to Ship Repair Estimates in Man-hoursFrom EverandA Guide to Ship Repair Estimates in Man-hoursRating: 4.5 out of 5 stars4.5/5 (5)
- Topic6 Time Cost Trade OffDocument22 pagesTopic6 Time Cost Trade OffBelan Omer100% (1)
- Diagnostic Fracture Injection Tests in Ultra Low Perm FormationsDocument6 pagesDiagnostic Fracture Injection Tests in Ultra Low Perm FormationsBolsec14No ratings yet
- Flow Analysis of Butterfly Valve Using CFDDocument7 pagesFlow Analysis of Butterfly Valve Using CFDIJMERNo ratings yet
- Hydrotest Method Statement 12th Mar 2012-1Document21 pagesHydrotest Method Statement 12th Mar 2012-1sethu1091100% (21)
- Drilling Problems N Drilling OptimizationDocument68 pagesDrilling Problems N Drilling Optimizationngecus67% (3)
- Flash Point Calculation by UNIFACDocument15 pagesFlash Point Calculation by UNIFACmertel_26No ratings yet
- Thermodynamics Applications in Chemical Engineerings and The Petroleum Industry, Jean Vidal, TecDocument406 pagesThermodynamics Applications in Chemical Engineerings and The Petroleum Industry, Jean Vidal, Tecphantanthanh100% (2)
- Met Questions SacaaDocument168 pagesMet Questions SacaaAnirudh Reddy100% (2)
- Guidelines for Estimating Greenhouse Gas Emissions of ADB Projects: Additional Guidance for Clean Energy ProjectsFrom EverandGuidelines for Estimating Greenhouse Gas Emissions of ADB Projects: Additional Guidance for Clean Energy ProjectsNo ratings yet
- Vapor Phase Drying For Moisture Removal From Transformer Coil InsulationDocument5 pagesVapor Phase Drying For Moisture Removal From Transformer Coil InsulationYashNo ratings yet
- Hydrotest Method Statement 12th Mar 2012 1Document21 pagesHydrotest Method Statement 12th Mar 2012 1Saut Maruli Tua Samosir100% (1)
- Detailed Solutions To ExercisesDocument123 pagesDetailed Solutions To Exerciseslutfi awn100% (5)
- Flow MeasurementDocument15 pagesFlow MeasurementPhongNo ratings yet
- Brosur - PolbanDocument2 pagesBrosur - PolbanSu Crez No AtmajaNo ratings yet
- 142SJJ JRP JJBvCME16HORIZONTALDIRECTIONALDRILLINGNEWERAFORDocument9 pages142SJJ JRP JJBvCME16HORIZONTALDIRECTIONALDRILLINGNEWERAFORnika2006No ratings yet
- Components HDDDocument9 pagesComponents HDDNafee AzmaniNo ratings yet
- Minor LossesDocument33 pagesMinor LossesAyesha SiddiqaNo ratings yet
- Pressure Buildups Vs Static Gradient Survey Flowing Gradient SurveyDocument1 pagePressure Buildups Vs Static Gradient Survey Flowing Gradient Surveyfadhli202100% (1)
- ConsolidationDocument14 pagesConsolidationSapria AdiNo ratings yet
- SPE 126108 HP/HT Well Intervention by Coil Tubing-East Coast Case HistoriesDocument9 pagesSPE 126108 HP/HT Well Intervention by Coil Tubing-East Coast Case Historiesharesh kumarNo ratings yet
- Mebs7014 2223 01Document66 pagesMebs7014 2223 01Yuki ChanNo ratings yet
- DuvalDocument12 pagesDuvalChemist Ahmed FoudaNo ratings yet
- Chapter 2:-: Faculty of Engineering Petroleum Engineering Department Production Engineering II Fourth StageDocument29 pagesChapter 2:-: Faculty of Engineering Petroleum Engineering Department Production Engineering II Fourth StageOmer IkhlasNo ratings yet
- Overview of Existing Work: Under The Supervision and GuidanceDocument26 pagesOverview of Existing Work: Under The Supervision and Guidanceharsh agarwalNo ratings yet
- 42" Export Pipeline Project Status: Always Moving ForwardDocument14 pages42" Export Pipeline Project Status: Always Moving Forwardtulasirao.nammiNo ratings yet
- FALL 2021 2022 MKT3871 Week03 - Transfer of Momentum and ApplicationsDocument36 pagesFALL 2021 2022 MKT3871 Week03 - Transfer of Momentum and ApplicationsAbdulaziz AlnajjarNo ratings yet
- Aerospace Thermodynamics AS2007: DR Surendra GhadaiDocument35 pagesAerospace Thermodynamics AS2007: DR Surendra Ghadaimaaz ahmadNo ratings yet
- Gas Lift ThesisDocument8 pagesGas Lift Thesisfjbr4n2n100% (2)
- Simulation of Drilling Pressure Profile in DirectiDocument7 pagesSimulation of Drilling Pressure Profile in DirectiSivaramanNo ratings yet
- Calc PWFDocument18 pagesCalc PWFgemsaproductionNo ratings yet
- Physics-Project 3Document11 pagesPhysics-Project 3Rajaram VishwakarmaNo ratings yet
- 513-Article Text-1583-1-10-20211115Document10 pages513-Article Text-1583-1-10-20211115hairieNo ratings yet
- ElectricityDocument96 pagesElectricityGangadhar RockNo ratings yet
- HYSYS - Htfs ExchangerDocument36 pagesHYSYS - Htfs ExchangerfsijestNo ratings yet
- TriptiDocument19 pagesTriptiTripti AgrawalNo ratings yet
- DST MajdobDocument12 pagesDST Majdobahmeda zayedNo ratings yet
- Model and Analysis of Desktop Wind Tunnel: Md. Khaleel, S. Alka, & Marampalli ShilpaDocument8 pagesModel and Analysis of Desktop Wind Tunnel: Md. Khaleel, S. Alka, & Marampalli ShilpaTJPRC PublicationsNo ratings yet
- Positioning of Splitter Vanes in Centrifugal Pumps 2Document9 pagesPositioning of Splitter Vanes in Centrifugal Pumps 280hoticeNo ratings yet
- Positioning of Splitter Vanes in Centrifugal Pumps 3Document7 pagesPositioning of Splitter Vanes in Centrifugal Pumps 380hoticeNo ratings yet
- Jay 1Document6 pagesJay 1DK MoviesNo ratings yet
- Thesis Online ChulaDocument7 pagesThesis Online Chulaangelagibbsdurham100% (2)
- Hydraulic Bridge: Physics ProjectDocument21 pagesHydraulic Bridge: Physics ProjectAlessandra0% (1)
- Thermoacoustic Engine and RefrigeratorDocument21 pagesThermoacoustic Engine and RefrigeratorSubhan UllahNo ratings yet
- EGU2020 11450 PresentationDocument30 pagesEGU2020 11450 PresentationmarwanNo ratings yet
- Spe 133268 MS PDFDocument18 pagesSpe 133268 MS PDFPhuc TruongNo ratings yet
- Fow Seng Joe (B1757) - FMI Lab 1 Impact JetDocument15 pagesFow Seng Joe (B1757) - FMI Lab 1 Impact JetRobert Fow JOENo ratings yet
- Afif 2020 J. Phys. - Conf. Ser. 1517 012062Document7 pagesAfif 2020 J. Phys. - Conf. Ser. 1517 012062Engineer BoyNo ratings yet
- Single and Multiphase CFD Simulations For Designing Cavitating VenturiDocument12 pagesSingle and Multiphase CFD Simulations For Designing Cavitating VenturiCarlos GamarraNo ratings yet
- PPE-3S-S2-Ch4-Lesson 4Document20 pagesPPE-3S-S2-Ch4-Lesson 4Omer IkhlasNo ratings yet
- Vertical Drain 4Document5 pagesVertical Drain 4Dian_SipilNo ratings yet
- Evaluating The Structural Strength of Flexible PavDocument29 pagesEvaluating The Structural Strength of Flexible PavKenneth DacasinNo ratings yet
- Thermodynamics 1 Chap#04 1Document44 pagesThermodynamics 1 Chap#04 1Mubashar HassanNo ratings yet
- FM Lab ManualDocument76 pagesFM Lab ManualsidharthNo ratings yet
- Evaluation of Technical Drilling OperationDocument56 pagesEvaluation of Technical Drilling OperationAkuffo TheophilusNo ratings yet
- Validation 1 - ENCIT2012-340Document8 pagesValidation 1 - ENCIT2012-340ahmed azizNo ratings yet
- Identifying Casing While Drilling (CWD) Potential in Geothermal Scenario Along With EconomicsDocument7 pagesIdentifying Casing While Drilling (CWD) Potential in Geothermal Scenario Along With EconomicsBelhadj Mohammed NafaaNo ratings yet
- Measurement of Threshold Capillary Pressure For Seal Rocks Using The Step-By-Step Approach and The Residual Pressure Approach-2011Document8 pagesMeasurement of Threshold Capillary Pressure For Seal Rocks Using The Step-By-Step Approach and The Residual Pressure Approach-2011是sherry吖No ratings yet
- Khanna's Qbjective Type QuestionsDocument878 pagesKhanna's Qbjective Type QuestionsarunNo ratings yet
- Final Year Mechanical Engg. Ground Source Cooling SystemDocument21 pagesFinal Year Mechanical Engg. Ground Source Cooling SystemrajanvidyarthiNo ratings yet
- A Crisis of More Area Than The Required Heat Exchanging Surface AreaDocument28 pagesA Crisis of More Area Than The Required Heat Exchanging Surface Areaavula43100% (1)
- Homework 5 - 2020 - 01 - v3 - YH (v3) - ALV (v2)Document5 pagesHomework 5 - 2020 - 01 - v3 - YH (v3) - ALV (v2)CARLOS DIDIER GÓMEZ ARCOSNo ratings yet
- Effects of Temperature in Phase Change of Matter Detailed Lesson PlanDocument11 pagesEffects of Temperature in Phase Change of Matter Detailed Lesson PlanJhana Kate FalculanNo ratings yet
- 02 - Heat Transfer MechanismDocument21 pages02 - Heat Transfer MechanismAndreana Amor GulayNo ratings yet
- Tutorial 1 CHM476Document3 pagesTutorial 1 CHM476PUTRI DAYANA BATRIESYA ABDUL HANIFNo ratings yet
- Trane 2TTB0060Document16 pagesTrane 2TTB0060Daniel Viñas BNo ratings yet
- Using KSP For The Dissolution of Borax in Water To Determine: G°, H° and S°Document4 pagesUsing KSP For The Dissolution of Borax in Water To Determine: G°, H° and S°Valentin-AngeloUzunov100% (18)
- Revista Mexicana de Ingeniería Química 1665-2738: Issn: Amidiq@xanum - Uam.mxDocument16 pagesRevista Mexicana de Ingeniería Química 1665-2738: Issn: Amidiq@xanum - Uam.mxEllen Gracia HindrawanNo ratings yet
- Lecture 2 BSE2201 Cooling Load CalculationDocument72 pagesLecture 2 BSE2201 Cooling Load CalculationBrian LiNo ratings yet
- SCV Series Screw CompressorDocument2 pagesSCV Series Screw CompressorCali MelendezNo ratings yet
- Chapter 4 - Transient Heat ConductionDocument18 pagesChapter 4 - Transient Heat ConductionMohsan HasanNo ratings yet
- Cooling Tower PowerPointDocument12 pagesCooling Tower PowerPointHaerNo ratings yet
- 02 Heat Question-BankDocument62 pages02 Heat Question-BankDébàshis Dash100% (1)
- HVACDocument58 pagesHVACAnonymous 6V5QyM1M3LNo ratings yet
- 2019 Recitation Chap 2 PDFDocument21 pages2019 Recitation Chap 2 PDFGull100% (1)
- Worksheet of ThermodynamicsDocument23 pagesWorksheet of Thermodynamicsdr.mohammed IkramNo ratings yet
- The Process Simulation Revolution: Thermophysical Property Needs and ConcernsDocument4 pagesThe Process Simulation Revolution: Thermophysical Property Needs and ConcernsMMHFNo ratings yet
- 26 - VRV Section of Daikin UK Product Catalogue 2010 - tcm46 188570 1 PDFDocument36 pages26 - VRV Section of Daikin UK Product Catalogue 2010 - tcm46 188570 1 PDFDaud Simon ANo ratings yet
- ASME Steam Tables - Compact EditionDocument32 pagesASME Steam Tables - Compact EditionPuput NurlizanNo ratings yet
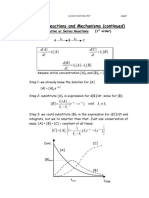
- Consecutive, Series, and Reversible ReactionsDocument6 pagesConsecutive, Series, and Reversible ReactionsRojo JohnNo ratings yet
- Ashrae Pocket Guide 2005 PDFDocument2 pagesAshrae Pocket Guide 2005 PDFDedi KartiwaNo ratings yet
- Exergy (Thermodynamics)Document4 pagesExergy (Thermodynamics)justdanish100% (1)