Probability

Continuous Random Variable-I

Some Special Continuous Distributions

Continuous Uniform Distribution (OR) Rectangular Distribution: A continuous

random variable x defined on [a, b] is said to have a uniform distribution, if its
probability density function is given by
 1
F(x) =  b − a ; forx ∈ [a, b]
0; otherwise

The cumulative distribution function of the continuous uniform random variable x is

given by
0; ifx ≤ a
x − a
F(x) =  ; ifa < x < b
b − a
1; ifx ≥ b

a+b
※Mean of x = µ =
2
(b − a)2
※Variance of x = σ = 2
12

Normal Distribution: A continuous random variable X is said to have a Normal

Distribution with parameters µ and σ2 if its density function is given by the
probability density function

−
(x − µ )2 − ∞ < x < ∞
 1 2 
 e 2σ − ∞ < µ < ∞ 
f (x ) = 
σ 2π
 σ>0 
 0 otherwise 
It is denoted as X ∼ N (µ, σ2)

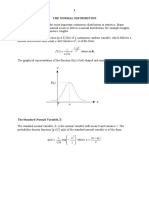
The graphical representation of normal distribution is as given below.

 Probability

34.13%
34.13%

13.59%
13.59%
2.14% 2.14%
µ − 2σ µ − σ µ µ + σ µ + 2σ

Properties of Normal Distribution

(i) The function is symmetrical about the valueµ.

(ii) It has a maximum at x = µ.

(iii) The area under the curve within the interval (µ ± σ) is 68%.
i.e. P (µ – σ ≤ x ≤ µ + σ) = 0.68.

(iv) A fairly large number of samples taken from a “Normal” population will have
average, median and mode nearly the same, and within the limits of average
±2 × S.D., there will be 95% of the values.

+∞
(v) E (X) = ∫ x . f (x ) dx = µ .
−∞

(vi) V (X) = σ2 ; S.D (X) = σ

(vii) For a normal distribution,

Mean = median = Mode.

(viii) All odd order moments about Mean vanish for a Normal Distribution.
i.e. µ 2n +1 = 0 ∀ = n = 0, 1, 2, …….

(ix) If X1 ∼ N (µ1, σ12) and X2 ∼ N (µ2, σ22), X1, X2 independent, then,

X1 + X2 ∼ N (µ1 + µ2, σ12 + σ22)
Also, X1 – X2 ∼ N (µ1 – µ2, σ12 + σ22)
 Probability

(x) If µ = 0 and σ² = 1, we call it as standard normal distribution. The

standardisation can be obtained by the transformation
x−µ X−µ
z= . Also, ∼ N (0, 1)
σ σ
Exponential Distribution: A continuous random variable x is said to have an
exponential distribution if its probability density function f(x) is given by
 − λx ; forx > 0
F(x) = λe
0; otherwise
Here λ is the parameter of the exponential distribution and λ > 0
The cumulative distribution function F(x) of an exponential distribution with λ as
parameter is
 − λx
F(x) = 1 − e ; if x > 0
0, otherwise
1
Mean = µ =
λ
1
Variance = σ2 =
λ2