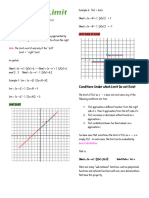
As mentioned previously, one condition for the

limit of a function as x approaches c from the left is

equal to the value of a function as x approaches c
from the right. Thus, the expression lim
�→�
�(�) always

denotes a two-sided limit.

ONE-SIDED LIMITS
One-sided limits are limits of a function as x
approaches c from either the left-hand side or the
right-hand side.
ONE-SIDED LIMITS
The limit of a function f at x = c as x approaches c
from the left-side is called the left-hand limit . In
evaluating the left-hand limit, only the values less than
c are considered. Otherwise, it is called a right-hand
limit.
LEFT-HAND AND RIGHT-HAND LIMITS
Let the function f be defined on the open interval
(x,c) such that c > x . If f approaches the number L as x
approaches c within (x,c), then L is called the left-hand
limit of f at c. This is written as:
���− �(�) = �
�→�
LEFT-HAND AND RIGHT-HAND LIMITS
Similarly, if f is defined on the open interval (x,c)
such that c < x and f approaches the number M as x
approaches c within (x,c), then the M is called the right-
hand limit of f at c. This is written as:
���+ �(�) = �
�→�
If the value of f (x) arbitrarily increases without
bound through positive values for all x sufficiently
close to c from both sides, without letting x equal to c,
then ���
�→�
�(�) = ∞
Likewise, if the value of f (x) arbitrarily decreases
without bound through negative values for all x
sufficiently close to c from both sides, without letting
x equal to c, then ���
�→�
�(�) =− ∞
VERTICAL ASYMPTOTES
Vertical asymptotes are vertical lines that a curve
approaches as it goes to infinity.
HORIZONTAL ASYMPTOTES
Horizontal asymptotes are horizontal lines that a
curve approaches as it goes to infinity.
We’ll see you on the next class <3