Class Notes: Integrals

I. Introduction to Integrals

Integrals are a fundamental concept in calculus, introduced by Sir Isaac Newton and
Gottfried Wilhelm Leibniz in the late 17th century.
They provide a way to find the accumulation or total of quantities, such as area, distance,
volume, and more.
Two main types of integrals: definite and indefinite.
II. Indefinite Integrals

Also known as antiderivatives.

Denoted as ∫f(x) dx, where f(x) is the function to be integrated.
The result is a new function F(x) + C, where F(x) is the antiderivative of f(x), and C is the
constant of integration.
Example: ∫2x dx = x^2 + C.
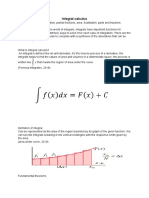
III. Definite Integrals

Used to find the net accumulation of a quantity over a specific interval.

Denoted as ∫[a, b] f(x) dx, where a and b are the limits of integration.
The result is a real number representing the accumulated quantity over [a, b].
Geometrically, it represents the area between the function curve and the x-axis from a to b.
Example: ∫[1, 3] x^2 dx = [1/3 * x^3] from 1 to 3 = (3^3/3) - (1^3/3) = 8.
IV. Fundamental Theorem of Calculus

Fundamental to the study of integrals.

States that if F(x) is an antiderivative of f(x) on an interval [a, b], then:

∫[a, b] f(x) dx = F(b) - F(a)

It provides a connection between differentiation and integration.

V. Methods of Integration

Various techniques are used to evaluate integrals, including:

Substitution method.
Integration by parts.
Trigonometric substitutions.
Partial fraction decomposition.
The choice of method depends on the form of the integrand.
VI. Applications of Integrals

Integrals have numerous real-world applications:

Calculating areas and volumes.
Determining displacement and velocity from acceleration.
Finding the center of mass of an object.
Solving problems in physics, economics, and engineering.
Probability and statistics (using probability density functions).
VII. Improper Integrals

Integrals that involve infinite limits or discontinuous functions.

Evaluated using limits, typically involving infinite series or integrals.
Example: ∫[1, ∞] 1/x dx = lim as a->∞ of ∫[1, a] 1/x dx = ∞.
VIII. Numerical Integration

Sometimes, it's impossible or impractical to find exact solutions analytically.

Numerical methods, like the trapezoidal rule or Simpson's rule, provide approximate
solutions by dividing the area into smaller pieces.
IX. Conclusion

Integrals are a powerful tool in mathematics with a wide range of applications.

They provide insights into accumulation and help solve real-world problems.
Mastery of integration techniques is essential for advanced calculus, physics, engineering,
and various scientific disciplines.