REVIEW – HYDRAULICS AND GEOTECHNICAL ENGINEERING

Base Units and Unit Pressures

Unit of Measure SI English

𝑚𝑚 𝑓𝑓𝑓𝑓
Acceleration
𝑠𝑠 2 𝑠𝑠 2
Area 𝑚𝑚2 𝑓𝑓𝑓𝑓 2
N ·m
Energy ft ·lb
(Joules)
Force Newton lb
Length m ft P: pressure gage
Mass Kg slug Pabs: absolute pressure
Area Moment of (If pressure is not specified, assume
Inertia 𝑚𝑚4 𝑓𝑓𝑓𝑓 4 gage)
𝑚𝑚
Momentum 𝑘𝑘𝑘𝑘 ∙ 𝑙𝑙𝑙𝑙 ∙ 𝑠𝑠
𝑠𝑠 Pabs = P + 1 atm
𝑙𝑙𝑙𝑙 1 atm = 14.7 psi = 101.3 kPa
Power watts 𝑓𝑓𝑓𝑓 ·
𝑠𝑠
𝑙𝑙𝑙𝑙 The pressure head in meters of a
Pressure Pa
𝑓𝑓𝑡𝑡 2 specified fluid:
Time s s 𝑃𝑃
𝑚𝑚 𝑓𝑓𝑓𝑓 ℎ=
Velocity 𝛾𝛾
𝑠𝑠 𝑠𝑠 Given two fluids A and B, the pressure
Volume 𝑚𝑚3 𝑓𝑓𝑓𝑓 3 head is:
Work
N ·m
ft ·lb 𝑆𝑆𝐺𝐺𝐴𝐴
ℎ𝐵𝐵 = ℎ
(Joules) 𝑆𝑆𝐺𝐺𝐵𝐵 𝐴𝐴
Other Formula:
𝑊𝑊𝑊𝑊𝑊𝑊𝑊𝑊ℎ𝑡𝑡
Manometers: Unit weight:𝛾𝛾 = 𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉 = 𝜌𝜌𝜌𝜌
An instrument for measuring the pressure 𝑀𝑀𝑀𝑀𝑀𝑀𝑀𝑀
Density: 𝜌𝜌 = 𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉𝑉
acting on a column of fluid, especially 𝛾𝛾
one with a U-shaped tube of liquid. Specific Gravity:𝑆𝑆𝑆𝑆 = 𝛾𝛾 = 𝜌𝜌/𝜌𝜌𝑤𝑤
𝑤𝑤
𝑁𝑁 𝑘𝑘𝑘𝑘
For a differential manometer, 𝛾𝛾𝑤𝑤 = 9810 3 𝜌𝜌𝑤𝑤 = 1000 3
𝑚𝑚 𝑚𝑚
𝛾𝛾
(For gases):𝑆𝑆𝑆𝑆 = 𝜸𝜸
𝒂𝒂𝒂𝒂𝒂𝒂
𝑁𝑁
𝛾𝛾𝑎𝑎𝑎𝑎𝑎𝑎 = 12 3
𝑚𝑚
Typical Specific Gravity Values:
Freshwater = 1.0
Seawater = 1.03
Oil = 0.80
Mercury = 13.6

Relationship of density, pressure and

density for air and other gases.
𝑃𝑃 = 𝜌𝜌𝜌𝜌𝜌𝜌

Where:
P = absolute pressure
ρ = density of gas
R = gas constant
T = temperature in Kelvin or Rankine

𝑝𝑝𝐴𝐴 + 𝛾𝛾1 ℎ1 − 𝛾𝛾1 ℎ1 − 𝛾𝛾1 ℎ1 = 𝑝𝑝𝐵𝐵 Sample Problems:

� 𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝, 𝑝𝑝 = 𝛾𝛾ℎ 1. One slug is equivalent to how many
kg?

2. What is the mass density of fresh

water in slugs per cubic foot?

INHINYERO REVIEW CENTER

 REVIEW – HYDRAULICS AND GEOTECHNICAL ENGINEERING

3. A body has a mass of 1.5 slugs in a P) at A and B is water and the specific
𝑚𝑚
place where 𝑔𝑔 = 9.81 𝑠𝑠2 , what is the mass gravity of mercury is 13.6.
in slugs where 𝑔𝑔 = 9.78 𝑚𝑚/𝑠𝑠 2 ?

4. A liquid in a 1.31 m3 container has a

mass of 1345 kg.
a. What is its mass density?
b. What is its specific gravity?
c. What is its gravity force?

5. A reservoir of glycerine has a mass

of 1200 kg and a volume of 0.952 cu. M.
Find its:
a. weight
b. density
c. specific weight
d. specific gravity
e. specific volume

6. The specific gravity of certain oil 13. Find the pressure at A.

is 0.82. Calculate its:
a. specific weight in lb/ft3
b. specific weight in kN/m3
c. mass density in slugs/ft3
d. mass density in kg/m3

7. A volume of water weighs about 9.75N.

Calculate its mass in kilograms.

8. If an object has a mass of 22 kg at

sea level, what will be its weight at a
point where the acceleration due to
gravity is 9.75 m/s2? What will be its
mass at that point?

9. A man weighs 70 kg. What is his

weight in lb and in N?

10. The pressure gage in a given tank

reads 92 mmHg. Determine the equivalent
height of column of oil, sg = 0.84. 14. Covert 98 gpm to cms.

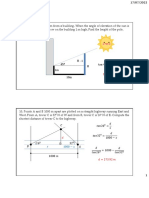
11. CE Board May 1998. A pressure gauge 15. Oil is flowing in a 0.1 m Φ pipe at
at elevation 8m at the side of a tank 3.5 m/s.
containing a liquid reads 80 kPa. a. What is the discharge in cms?
Another gauge at elevation 3m. reads 120 b. Find the flow rate in mgd
kPa. Compute the following: c. Find the weight flux in kN/s
a. specific weight of the fluid
b. density of the fluid 16. A gas is under pressure of 25 bar
c. specific gravity of the fluid absolute at 40-degree celcius.
a. Compute the pressure in kPa
12. A U tube manometer measures the b. Compute the gage pressure
pressure difference between two points A c. Compute the gas constant R in
and B in a liquid. The U tube contains m2/s2K if it has a unit weight of 360
mercury (fluid Q). Calculate the N/m3
difference in pressure if h =1.5 m, h2 =
0.75 m and h1 = 0.5 m. The liquid (fluid

INHINYERO REVIEW CENTER

 REVIEW – HYDRAULICS AND GEOTECHNICAL ENGINEERING
Total Hydrostatic Pressures:
A. Plane Surfaces
� 𝑨𝑨
𝑭𝑭 = 𝜸𝜸𝒉𝒉
at c.p. (total hydrostatic pressure on
plane area A subjected to liquid)
The distance between the centroid (c)
and center of pressure (c.p.) along the
body is called eccentricity (e).
𝒆𝒆 = 𝑰𝑰�/𝑨𝑨𝒚𝒚
� b. Find the location of the force from
� – distance of the centroid below the
𝒉𝒉
liquid surface on the vertical (m)
� – distance of the centroid below the
𝒚𝒚
liquid surface along the body (m)
�𝑰𝑰 – moment of inertia of A with respect
to its centroidal axis (m4)
Sample Problems:
1. A triangular gate with a horizontal
base 1.2 m long and an altitude of 1.8 m
is inclined 45° from the vertical with
the vertex pointing upward. The hinged
horizontal base of the gate is 2.7 m
below the water surface.
a. Calculate the total force of the
water on the gate
b. How far is the said force from
the vertex measured along the gate?
c. What normal force must be applied
at the vertex of the gate to open it?
2. A vertical rectangular gate on the
face of the dam is 2 m wide and 4 m
high. The upper edge is 3 m below the
water surface.
a. Find the total force of water on
the gate
b. How far is the said force from
the bottom of the gate?
c. If the gate is hinged at top, how
much horizontal force applied at the
bottom is needed to open it?
3. From the liquid surface, determine
the distance of the center of pressure
of the following:
a. A triangle of base b and height d
as vertical and submerged in a liquid
with its vertex at the liquid surface.
b. A circular area of diameter d and
submerged in a liquid. Its upper edge
coincides with the liquid surface.
c. A vertical semi-circular area of
diameter d and radius r is submerged
and has its diameter in a liquid
surface.
4. Tank abcd is 2.4 m wide and 6 m
long.
a. Compute the magnitude of the force on
wall ab
the bottom
c. Total force in the bottom of the
tank
B. Curved Surfaces
P = total hydrostatic pressure on a
curved surface
𝑃𝑃 = �𝑃𝑃ℎ2 + 𝑃𝑃𝑣𝑣 2
Ph - horizontal component; total
hydrostatic pressure on plane area “A”
which is the projection of the curved
surface on the vertical
Ph = 𝛾𝛾ℎ�𝐴𝐴 (projected area)
INHINYERO REVIEW CENTER
 REVIEW – HYDRAULICS AND GEOTECHNICAL ENGINEERING

2. Curve “mn” shown is a quarter circle

with radius of 5 m. For a length of 3 m
perpendicular to the paper, determine:
a. The horizontal force acting on the
curve
b. The vertical force acting on the
curve
c. The total force on the curve

𝑷𝑷𝒗𝒗 - vertical component; weight of liquid

whose volume is traced by moving the
curve vertically upward until the liquid
surface (prolongation)
𝑷𝑷𝒗𝒗 = 𝜸𝜸𝜸𝜸𝜸𝜸𝜸𝜸

Liquid below Surface

Sample Problems:
1. The face of the 50-m long dam shown
is a quarter circle with radius 20 m.

a. Calculate the vertical component of

the force of water on the dam
b. Determine the angle of the
resultant force of water with respect
to the horizontal

INHINYERO REVIEW CENTER