ENGR 387

Vibration of Mechanical Systems

Free damped vibration, Log decrement
(Rao: 2.6, 2.9*, 2.10* | Inman: 1.3)

Milad Ramezankhani, PhD Candidate

Winter 2021

Engineering Vibration, 4th Edition, Daniel J. Inman

0
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Viscous damping

Engineering Vibration, 4th Edition, Daniel J. Inman

1
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Viscous damping

• The viscous damping force F is proportional to the velocity 𝑥𝑥̇ and can be
expressed as:

• where c is the damping constant or coefficient of viscous damping

• The negative sign indicates that the damping force is opposite to the direction
of velocity.

Engineering Vibration, 4th Edition, Daniel J. Inman

2
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Single-degree-of-freedom system with a
viscous damper

Engineering Vibration, 4th Edition, Daniel J. Inman

3
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Solution of the equation of motion

Engineering Vibration, 4th Edition, Daniel J. Inman

4
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Critical damping

• The critical damping 𝑐𝑐𝑐𝑐 is defined as the value of the damping

constant 𝑐𝑐 for which the radical in becomes zero:

Engineering Vibration, 4th Edition, Daniel J. Inman

5
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Damping ratio

• For any damped system, the damping ratio 𝜁𝜁 is defined as the

ratio of the damping constant to the critical damping constant:

Engineering Vibration, 4th Edition, Daniel J. Inman

6
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Damping ratio and critical damping

Engineering Vibration, 4th Edition, Daniel J. Inman

7
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
 Damping ratio and critical damping

The nature of the roots s1 and s2 and hence the behavior of the solution above,
depends upon the magnitude of damping.

Engineering Vibration, 4th Edition, Daniel J. Inman

8
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Engineering Vibration, 4th Edition, Daniel J. Inman
9
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Engineering Vibration, 4th Edition, Daniel J. Inman
10
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
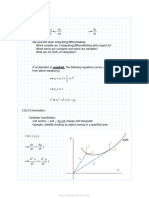
This is a damped harmonic motion of angular frequency , but because of the factor
, the amplitude decreases exponentially with time.

Engineering Vibration, 4th Edition, Daniel J. Inman

11
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Frequency of damped vibration

Engineering Vibration, 4th Edition, Daniel J. Inman

12
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Engineering Vibration, 4th Edition, Daniel J. Inman
13
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Engineering Vibration, 4th Edition, Daniel J. Inman
14
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Comparison of motions with different types of damping

Engineering Vibration, 4th Edition, Daniel J. Inman

15
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Phase plane of a damped system

Engineering Vibration, 4th Edition, Daniel J. Inman

16
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Example 1

Engineering Vibration, 4th Edition, Daniel J. Inman

17
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Example 2

Engineering Vibration, 4th Edition, Daniel J. Inman

18
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Example 3

Engineering Vibration, 4th Edition, Daniel J. Inman

19
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Logarithmic decrement
• The logarithmic (log) decrement represents the rate at which the amplitude of
a free-damped vibration decreases.
• It is defined as the natural logarithm of the ratio of any two successive
amplitudes (measured one cycle apart).
• Application: estimate the damping coefficient (𝜉𝜉) experimentally.

Engineering Vibration, 4th Edition, Daniel J. Inman

20
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Logarithmic decrement

Engineering Vibration, 4th Edition, Daniel J. Inman

21
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Logarithmic decrement

Engineering Vibration, 4th Edition, Daniel J. Inman

22
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Logarithmic decrement

Example:

Engineering Vibration, 4th Edition, Daniel J. Inman

23
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Example 4

Engineering Vibration, 4th Edition, Daniel J. Inman

24
Mechanical Vibrations, 6th Edition, Singiresu S. Rao
Energy dissipated in viscous damping

Engineering Vibration, 4th Edition, Daniel J. Inman

25
Mechanical Vibrations, 6th Edition, Singiresu S. Rao