Professional Documents
Culture Documents
Lecture 3 Porosity Measurement
Lecture 3 Porosity Measurement
Uploaded by
Saroo BastkyCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Lecture 3 Porosity Measurement
Lecture 3 Porosity Measurement
Uploaded by
Saroo BastkyCopyright:
Available Formats
Reservoir Rock Properties Lab.
Porosity
From the viewpoint of petroleum engineers one of the most important properties of a reservoir
rock is porosity. Porosity is a measure of storage capacity of a reservoir. It is defined as the ratio
of the pore volume to bulk volume, and it may be expressed as either a percent or a fraction,
Two types of porosity are total or absolute porosity and effective porosity. Total porosity is the
ratio of all the pore spaces in a rock to the bulk volume of the rock while the effective porosity
øe is the ratio of interconnected void spaces to the bulk volume. Thus, only the effective porosity
contains fluids that can be produced from wells. For granular materials such as sandstone, the
effective porosity may approach the total porosity, however, for shales and for highly cemented
or vugular rocks such as some limestones, large variations may exist between effective and total
porosity.
Porosity may be classified according to its origin as either primary or secondary. Primary or
original porosity developed during deposition of the sediment. Secondary porosity is caused by
some geologic process subsequent to formation of the deposit..
Figure 1: Cubic packing (a), rhombohedral (b), cubic packing with two grain sizes (c), and typical sand
with irregular grain shape (d).
Grain size distribution and sorting can influence the porosity. For a uniform rock grain size,
porosity is independent of the size of the grains. A maximum theoretical porosity of 48% is
achieved with cubic packing of spherical grains, as shown in Fig.1a. Rhombohedral packing, which
is more representative of reservoir conditions, is shown in Fig.1b; the porosity for this packing is
26%. Typical reservoir sand is illustrated in Fig. 1d.
Petroleum Eng. Dept. Page 1
Reservoir Rock Properties Lab.
Porosity measurement on core plugs:
The porosity of reservoir rock may be determined by using core analysis, well logging technique
or well testing. The porosity determined from core analysis has the advantage that no assumption
needs to be made as to mineral composition, borehole effects, etc. However, since the volume
of the core is less than the rock volume which is investigated by a logging device, porosity values
derived from logs are frequently more accurate in the case of heterogeneous reservoirs.
From the definition of porosity, it is evident that the porosity of a sample of porous material can
be determined by measuring any two of the three quantities: bulk volume, pore volume or grain
volume from core plugs.
Bulk volume:
Although the bulk volume may be computed from measurements of the dimensions of a
uniformly shaped sample, the usual procedure utilizes the observation of the volume of fluid
displaced by the sample. The fluid displaced by a sample can be observed either volumetrically
or gravimetrically. In either procedure it is necessary to prevent the fluid penetration into the
pore space of the rock. This can be accomplished by:
(1) Coating the sample with a thin layer of wax (paraffin) or a similar substance (varnish),
(2) Saturating the core with the fluid into which it is to be immersed, or
(3) Using mercury.
Gravimetric determinations of bulk volume can be accomplished by observing the loss in the
weight of the sample when immersed in a fluid or by change in weight of a pycnometer with and
without the core sample.
Pore volume:
All the methods measuring pore volume yield effective porosity. The methods are based on
either the extraction of a fluid from the rock or the introduction of a fluid into the pore spaces of
the rock. One of the commonly used methods is the helium technique, which employs Boyle's
law. The Helium porosimeter apparatus is shown in Figure 2.
Helium has the following advantages over other gases:
(I) Its small molecules rapidly penetrate into small pores.
(2) It is an inert gas and does not adsorb on rock surfaces (air may do),
(3) It can be an ideal gas (i.e., z = 1.0) for pressures and temperatures usually used in the test,
(4) It has a high diffusivity so affords a useful mean for determining porosity of low permeability
rocks.
Petroleum Eng. Dept. Page 2
Reservoir Rock Properties Lab.
Fig. 2: Schematic diagram of helium porosimeter apparatus.
The schematic diagram of the helium porosimeter shown in Fig. 2 has a reference volume V1, at
pressure p1, and a sample chamber with unknown volume V2, and initial pressure p2. The
reference cell and the sample cup are connected by tubing; the system can be brought to
equilibrium when the core holder valve is opened, allowing determination of the unknown
volume V2 by measuring the resultant equilibrium pressure p. Boyle’s law is applicable if the
expansion takes place isothermally.
Grain Volume Measurement
The grain volume of core samples is sometimes calculated from sample weight and knowledge
of average density. Boyle’s law is often employed with helium as the gas to determine grain
volume. The technique is fairly rapid, and is valid on clean and dry sample.
The measurement of the grain volume of a core sample may also be based on the loss in weight
of a saturated sample plunged in a liquid. Grain volume may be measured by crushing a dry and
clean core sample. The volume of crushed sample is then determined by (either pycnometer or)
immersing in a suitable liquid.
MATRIX VOLUME FROM GAS EXPANSION METHOD
Very accurate, especially for samples with low porosities
• Initial conditions, with volumes of 2 cells known
• Place core in second cell, evacuate gas (air) from second cell
• Open valve
Petroleum Eng. Dept. Page 3
Reservoir Rock Properties Lab.
• With V1 known, record p1
• p1 = pressure at initial conditions
• V1 = Volume of cell 1
• Place cleaned, dried core sample in cell 2
• Evacuate cell 2
• Open valve
This method assumes that the core becomes saturated with the gas. Incomplete saturation
would lead to an overestimate of the matrix volume.
• 𝑉𝑓 = Volume of Cell 1 + Volume of Cell 2 - Matrix Volume of Core
• 𝑉𝑡 = Volume of Cell 1 + Volume of Cell 2
• 𝑉𝑚 = 𝑉𝑡 - 𝑉𝑓
• Vb = the bulk volume of core, cm3.
• øe = (Vb-Vm)/Vb effective (interconnected) porosity of the core, fraction.
PORE VOLUME FROM GAS EXPANSION METHOD:
Pore volume measurements can be done by using the Boyle’s law, where the sample is placed
in a rubber sleeve holder that has no voids space around the periphery of the core and on the
ends. Such a holder is called the Hassler holder, making the volume of Cell 2 equal to the bulk
volume. Helium or one of its substitutes is injected into the core plug through the end stem.
Petroleum Eng. Dept. Page 4
Reservoir Rock Properties Lab.
This method is a continuation of the measurement of the matrix volume and uses Boyle’s law.
The experiment is set up differently to measure pore volume.
Boyle’s law:
Initial cell conditions: measure V1 in Cell 1 Put core in Hassler sleeve, then evacuate and open
valve.
To determine pore volume using ideal gas law at constant T:
𝑝1 𝑣1 = 𝑝2 𝑣2
Where
𝑣2 = Volume of first chamber and pore volume of core
𝑣𝑝 = 𝑣2 − 𝑣1
Vb = the bulk volume of core, cm3.
øe = (Vb-Vg)/Vb effective (interconnected) porosity of the core, fraction.
The gas expansion method (Boyle’s law method) is probably the preferred method for
measurement of core porosity. The method is preferable for poorly consolidated samples that
require a rubber sleeve or jacket. The measurement can be made at confining pressures
approximating reservoir stress conditions.
Example
A calibration procedure resulted in V1 = 100 cc and V2 = 80 cc, respectively. A core sample was
placed in the first chamber at 0 kPa pressure. Gas was admitted to the second chamber to a
Petroleum Eng. Dept. Page 5
Reservoir Rock Properties Lab.
pressure of 413.7 kPa. The valve was open and the final equalized pressure was recorded as
199.783 kPa. What is the grain volume?
Solution:
𝑝1 𝑣1 = 𝑝2 𝑣2
80 x 413.7 = 199.783 x Vf
Vf = 165.66 cc
Vgrain = Vt – Vf
= 100 + 80 – 165.66 = 14.34 cc
Gravimetric Method (Archimedes Method):
Archimedes principle: buoyant force is equal to the weight of the fluid displaced.
𝑉𝑝 = Pore volume, cm3
𝑊𝑠𝑎𝑡 = Weight of core saturated with fluid, g
𝑊𝑠𝑢𝑏 = Weight of saturated sample submerged in water, g
𝑊𝑑𝑟𝑦 = Weight of dry core, g
𝜌𝑓 = Density of saturated fluid, gm/cm
Petroleum Eng. Dept. Page 6
Reservoir Rock Properties Lab.
Example
Archimedes Method of Calculating Porosity a Core Sample
Using the gravimetric method with the following data, calculate the pore and bulk volumes and
the porosity. Is this porosity total or effective?
Dry weight of sample, 𝑊 𝑑𝑟𝑦 = 427.3 g
Weight of sample saturated with water, 𝑊 𝑠𝑎𝑡 = 448.6 g
Density of water (f ) = 1.0 g/cm3
Weight of saturated sample submerged in water, 𝑊 𝑠𝑢𝑏 = 269.6 g
Solution:
When a rock has a small fraction of void space, it is difficult to measure porosity by the mentioned
methods. At this case, mercury injection (Fig. 3a) is used. The principle consists of forcing mercury
under relatively high pressure in the rock pores. A pressure gauge is attached to the cylinder for
reading pressure under which measuring fluid is forced into the pores. (Fig. 3b) shows a typical
curve from the mercury injection method. The volume of mercury entering the core sample is
obtained from the device with accuracy up to 0.01 cm3.
Fig. 3: Mercury injection pump (a) and porosity through mercury injection (b)
Petroleum Eng. Dept. Page 7
Reservoir Rock Properties Lab.
Porosity Determination by Liquid Saturating Method
Description:
The determination of the effective liquid porosity of a porous plug is the initial part of the
measurement of capillary pressure using porous plate method in core laboratories. Before the
capillary pressure is determined the volume of the saturating liquid (brine or oil) in the core must
be known. Thus, the effective liquid porosity of the core can be calculated in the beginning of
capillary pressure measurement.
Procedure:
1. Weigh dry plug Wdry, measure its diameter D, and length L, with caliper (1 core for each group).
2. Put the cores in the beaker inside a vacuum container, run vacuum pump about 1 hour.
3. Saturate the cores with 36 g/l NaCl brine, ρbrine = 1.02g/cm3.
4. Weigh the saturated cores, Wsat.
Calculations and report:
1. Calculate the saturated brine weight, Wbrine = Wsat-Wdry.
2. Calculate the pore volume (saturated brine volume), Vp = Wsat/ρbrine.
3. Calculate effective porosity, øe = Vp/Vb.
Example 1
An irregular piece of sandstone is 35.25 grams in mass. When coated with varnish, its mass
increased to 36.55 grams. Compute the rock porosity if the coated sample displaces 15.7 ml of
water when fully submerged. ρg = 2.65 g/cm3, ρw = 1.00 g/cm3, ρv = 1.80 g/cm3.
Solution
Vg = 35.25 / 2.65 = 13.30 cm3
Vv = (36.55 – 35.25) / 1.80 = 0.72 cm3
Vb = 15.70 – 0.72 = 14.98 cm3
ϕ = (14.98 – 13.3) / 14.98 = 0.112 = 11.2%
Note: This value is the absolute porosity.
Example 2
Petroleum Eng. Dept. Page 8
Reservoir Rock Properties Lab.
The varnish coating on the sample of example 1 was removed and the sample was submerged in
water. When air bubbling stopped, the sample was weighed while suspended in water. It weighed
21300 dynes. Assume that you don't know the rock composition, compute the rock porosity.
Solution
Weight of sample in air = 35.25 x 980 = 34,545 dynes
Weight of sample in water = 21,300 dynes
Weight of displaced water = 34545 – 21300 = 13,245 dynes
Volume of displaced water = 13245 / (980 x 1) = 13.52 cm3
Vg = 13.52 cm3
ϕ = (14.98 – 13.52) / 14.98 = 0.097 = 9.7%
Note: This value is the effective porosity.
MATRIX DENSITIES (m) OF TYPICAL PURE COMPONENTS OF RESERVOIR ROCK
Lithology Matrix Density
(g/cm3)
Sandstone 2.65
Limestone 2.71
Dolomite 2.87
Bulk Volume Calculated by Displacement:
Example 3: A core sample coated with paraffin immersed in a container of liquid displaced 10.9
cm3 of the liquid. The weight of the dry core sample was 20.0 g, while the weight of the dry
sample coated with paraffin was 20.9 g. Assume the density of the solid paraffin is 0.9 g/cm 3.
Calculate the bulk volume of the sample.
Weight of paraffin coating, Wparaffin =
Weight of dry core sample coated with paraffin - Weight of dry core sample
Wparaffin = 20.9 g = 20.0 g = 0.9 g
Volume of paraffin coating = Weight of paraffin / density of paraffin
Vparaffin = 0.9 g / 0.9 g/cm3 = 1.0 cm3
Bulk volume of core sample = (Bulk volume of core coated with paraffin) – (volume of paraffin)
Vb = 10.9 cm3 – 1.0 cm3 = 9.9 cm3
Example 4
Petroleum Eng. Dept. Page 9
Reservoir Rock Properties Lab.
Calculating the Matrix Volume and Porosity of a Core Sample Using the Displacement Method
The core sample from Example 3 was stripped of the paraffin coat, crushed to grain size, and
immersed in a container with liquid. The volume of liquid displaced by the grains was 7.7 cm3.
Calculate the matrix volume and the core porosity. Is this effective porosity or total porosity?
(It is total porosity).
Solution:
Bulk Volume, Vb = 9.9 cm3
Matrix Volume, Vma = 7.7 cm3
Vp Vb − Vma 9.9 – 7.7
𝑃𝑜𝑟𝑜𝑠𝑖𝑡𝑦 = ∅ = = = = 0.22 = 22% (Total Porosity)
Vb Vb 9.9
Petroleum Eng. Dept. Page 10
You might also like
- 2019 RAM 1500 Classic Big Horn 3.6LDocument139 pages2019 RAM 1500 Classic Big Horn 3.6LguillebohlNo ratings yet
- Drilling Mud CalculationDocument12 pagesDrilling Mud Calculationaditya imansyahNo ratings yet
- Benzodiazepine and Z Drug Resource Pack GMMMG FINAL v1 0 For GMMMG WebsiteDocument59 pagesBenzodiazepine and Z Drug Resource Pack GMMMG FINAL v1 0 For GMMMG WebsiteAaronNo ratings yet
- Set 1 PDFDocument3 pagesSet 1 PDFOmer IkhlasNo ratings yet
- Properties of Wet GasesDocument18 pagesProperties of Wet GasesAlejandro Perez100% (1)
- Chapter 3 Permeability Part 3Document14 pagesChapter 3 Permeability Part 3PugalNo ratings yet
- Drilling BOPsDocument12 pagesDrilling BOPsSaroo MusicNo ratings yet
- PET524 1b PorosityDocument8 pagesPET524 1b PorosityzsiddiquiNo ratings yet
- Porosity Measurement by Helium Porosimetery MethodDocument5 pagesPorosity Measurement by Helium Porosimetery MethodAhmad Mu'tasimNo ratings yet
- Rock Permeability: Reservoir Rock Properties LabDocument12 pagesRock Permeability: Reservoir Rock Properties LabhashoNo ratings yet
- Gas Well Testing HandbookDocument2 pagesGas Well Testing Handbookjose david CardozoNo ratings yet
- Example 3 Relating Downhole Rate With The Rate at Standard ConditionsDocument8 pagesExample 3 Relating Downhole Rate With The Rate at Standard ConditionsMaisam AbbasNo ratings yet
- Brihad Bhagavatamrita 1Document81 pagesBrihad Bhagavatamrita 1nitai1008100% (1)
- 00.0 DKFG 1-2Document113 pages00.0 DKFG 1-2wisdom seeker100% (3)
- Differential Liberation TestDocument19 pagesDifferential Liberation Testndlr81100% (1)
- Bhs. Inggris Kelas 4Document4 pagesBhs. Inggris Kelas 4dulsetosezNo ratings yet
- Reservoir Lab SheetDocument36 pagesReservoir Lab SheetSteve Lian Kuling100% (1)
- Porosity by Saturation Method-150731201424-Lva1-App6891Document16 pagesPorosity by Saturation Method-150731201424-Lva1-App6891Mohammed AL-sharafiNo ratings yet
- Experiment On Sand ContentDocument15 pagesExperiment On Sand ContentAnsell EwemeNo ratings yet
- Yield of ClayDocument7 pagesYield of ClayMohammed Ali AlnooriNo ratings yet
- Reservoir Laboratory: Exp Name: Bulk Volume MeasurementDocument5 pagesReservoir Laboratory: Exp Name: Bulk Volume MeasurementAvericl H n v ejkeNo ratings yet
- Funnel Viscosity Lab.2Document11 pagesFunnel Viscosity Lab.2Lulav BarwaryNo ratings yet
- 02 - Pore Space PropertiesDocument54 pages02 - Pore Space PropertiesNhi VoNo ratings yet
- Lab 3 Porosity Determination Using Helium Porosimeter MethodDocument6 pagesLab 3 Porosity Determination Using Helium Porosimeter MethodRichard OwusuNo ratings yet
- Sand Content: University of Zawia Faculty of Oil & Gas Engineering Drilling Fluid Lab ExperimentDocument6 pagesSand Content: University of Zawia Faculty of Oil & Gas Engineering Drilling Fluid Lab Experimentايمن القنونيNo ratings yet
- Cleaning and Saturation Determination: Reservoir Rock Properties LabDocument6 pagesCleaning and Saturation Determination: Reservoir Rock Properties LabMohammef MohammedNo ratings yet
- Porosity QuestionsDocument3 pagesPorosity QuestionsAtahan AltayNo ratings yet
- PET 310E Experiment #1 Page 1 of 10 Drilling and Completion Fluids LaboratoryDocument10 pagesPET 310E Experiment #1 Page 1 of 10 Drilling and Completion Fluids LaboratoryEmin KaragözNo ratings yet
- Oil Well TestingDocument5 pagesOil Well TestingRizwan FaridNo ratings yet
- Reserve Estimation Methods - 00 - IntroductionDocument4 pagesReserve Estimation Methods - 00 - Introductionviya7No ratings yet
- Predicting Hydrocarbon Recovery - AAPG WikiDocument3 pagesPredicting Hydrocarbon Recovery - AAPG WikiWassef MBNo ratings yet
- Reservoir Rock Properties Lab.: Capillary PressureDocument6 pagesReservoir Rock Properties Lab.: Capillary PressureHeven HassanNo ratings yet
- Lab ManualDocument17 pagesLab ManualMuhammad SaifuddinNo ratings yet
- Density Log: DR Bijaya K BeheraDocument20 pagesDensity Log: DR Bijaya K BeheraSagar DadhichNo ratings yet
- Lab 3-To Measure The Absolute Porosity of A Given Core Sample GravimetricallyDocument13 pagesLab 3-To Measure The Absolute Porosity of A Given Core Sample GravimetricallySunny BbaNo ratings yet
- Viscosity Flow Time RelationDocument7 pagesViscosity Flow Time Relationm_k_tripathyNo ratings yet
- Reservoir Engineering Lab REPORT SESSION/SEM: 20212022/1: Experiment No. Title Section Group No. Group MembersDocument11 pagesReservoir Engineering Lab REPORT SESSION/SEM: 20212022/1: Experiment No. Title Section Group No. Group MembersDHANASEELAN A/L V G PRAGASAM A19ET0053No ratings yet
- Experiment On Hydrogen Ion ConcentrationDocument15 pagesExperiment On Hydrogen Ion ConcentrationAnsell EwemeNo ratings yet
- Lab 3Document13 pagesLab 3ismael hashiNo ratings yet
- Drilling Engineering Lab.3.: Mud DilutionDocument10 pagesDrilling Engineering Lab.3.: Mud DilutionLulav BarwaryNo ratings yet
- Ararat Private Technical InstituteDocument14 pagesArarat Private Technical InstituteKhairy Omer100% (1)
- Lab 1-Measurement of Density of Drilling Mud Samples Using Mud Balance.Document15 pagesLab 1-Measurement of Density of Drilling Mud Samples Using Mud Balance.Sunny BbaNo ratings yet
- Sand Content 1Document4 pagesSand Content 1ايمن القنونيNo ratings yet
- Material Balance in Saturated ReservoirDocument5 pagesMaterial Balance in Saturated ReservoirSPE Call for WritingNo ratings yet
- Well-Logging Lab No. 6 - Porosity Logs.Document4 pagesWell-Logging Lab No. 6 - Porosity Logs.Sam AhmedNo ratings yet
- Experiment No. 6 Mud ResistivityDocument3 pagesExperiment No. 6 Mud ResistivityAlimahmood BahraniNo ratings yet
- Mud Densities Exp NewDocument8 pagesMud Densities Exp NewHafizszul FeyzulNo ratings yet
- Reservior Petrophysics LabDocument55 pagesReservior Petrophysics Labhussein alsaedeNo ratings yet
- 1D PetroMod Software Modeling of The Basrah Oil Fields Art-3A10.1007-2Fs12517-012-0640-4Document26 pages1D PetroMod Software Modeling of The Basrah Oil Fields Art-3A10.1007-2Fs12517-012-0640-4Charles PaikiNo ratings yet
- RFT ManualDocument14 pagesRFT Manualmazhar badrNo ratings yet
- خواص صخور المكمن رقم 1Document30 pagesخواص صخور المكمن رقم 1maamoun ramyNo ratings yet
- 26 Properties of Reservoir RockDocument33 pages26 Properties of Reservoir RockWahyudi Mufti100% (1)
- Abdullwahid Ahmed EXPDocument14 pagesAbdullwahid Ahmed EXPAbdullwahid AhmedNo ratings yet
- Ex2 PDFDocument1 pageEx2 PDFMusab UsmanNo ratings yet
- Tutorial 2Document3 pagesTutorial 2علي حسين جميلNo ratings yet
- Lab Report Permeability MeasurementDocument9 pagesLab Report Permeability Measurementsher afganNo ratings yet
- Cementing 1 PDFDocument20 pagesCementing 1 PDFSagar DadhichNo ratings yet
- Exercise 2-Material Balance Calculations (Zero-Dimensional Analysis)Document1 pageExercise 2-Material Balance Calculations (Zero-Dimensional Analysis)Albertlb ABNo ratings yet
- Material Balance MSC 2 2013Document21 pagesMaterial Balance MSC 2 2013Karwan DilmanyNo ratings yet
- Pansystem Analysis of Drawdown and Build-Up TestDocument11 pagesPansystem Analysis of Drawdown and Build-Up TestSayaf SalmanNo ratings yet
- Lecture 5. Neutron LoggingDocument72 pagesLecture 5. Neutron LoggingDimash AbdrakhmanovNo ratings yet
- Caliper Logs: Instructor: Hamad Ur Rahim Class: DDE Semester: IIIDocument19 pagesCaliper Logs: Instructor: Hamad Ur Rahim Class: DDE Semester: IIINaser KhanNo ratings yet
- Lab 4-Measurement of Plastic Viscosity of Different Mud Samples by Viscometer.Document20 pagesLab 4-Measurement of Plastic Viscosity of Different Mud Samples by Viscometer.Sunny BbaNo ratings yet
- Saturating Method Porosity Determination by LiquidDocument9 pagesSaturating Method Porosity Determination by Liquidali ahmedNo ratings yet
- Koya University Faculty of Engineering School of Petroleum and Chemical Reservior LabDocument16 pagesKoya University Faculty of Engineering School of Petroleum and Chemical Reservior LabBakomora Evans WilliamsNo ratings yet
- Sulaimani Polytechnic University (SPU) : Oil & Energy EngineeringDocument8 pagesSulaimani Polytechnic University (SPU) : Oil & Energy Engineeringrebaz omerNo ratings yet
- Seismic Refraction MethodDocument9 pagesSeismic Refraction MethodSaroo MusicNo ratings yet
- Introduction To The Refraction Method in GeophysicsDocument10 pagesIntroduction To The Refraction Method in GeophysicsSaroo MusicNo ratings yet
- Drlling Mud Grupe C1Document22 pagesDrlling Mud Grupe C1Saroo MusicNo ratings yet
- Sarmand 1Document19 pagesSarmand 1Saroo MusicNo ratings yet
- Cleaning and Saturation DeterminationDocument7 pagesCleaning and Saturation DeterminationSaroo MusicNo ratings yet
- Core and Plug PreparationDocument7 pagesCore and Plug PreparationSaroo MusicNo ratings yet
- GraniteDocument2 pagesGraniteSaroo MusicNo ratings yet
- Juki 1790Document2 pagesJuki 1790dharmik borisagarNo ratings yet
- Class-6 MarhsDocument6 pagesClass-6 Marhsrameshdorage12No ratings yet
- Vision RX Lab Private Limited P-4, Kasba Industrial Estate, Phase - 1, Kolkata - 107Document1 pageVision RX Lab Private Limited P-4, Kasba Industrial Estate, Phase - 1, Kolkata - 107Pravin KhopadeNo ratings yet
- Ril Sa71m15017693 R00Document5 pagesRil Sa71m15017693 R00Android100% (1)
- AnswersPractice Problems - Unit 3 - Open Up ResourcesDocument32 pagesAnswersPractice Problems - Unit 3 - Open Up ResourcesJa'Kyah Allen Student - WakeForestMSNo ratings yet
- StrabismusDocument61 pagesStrabismusOmesh PrathirajaNo ratings yet
- Human Body Temperature Measurement ListDocument2 pagesHuman Body Temperature Measurement ListproNo ratings yet
- List Besaran Diskon Maksimal Per Produk: NO Kode Produk Komposisi Kemasan HNADocument10 pagesList Besaran Diskon Maksimal Per Produk: NO Kode Produk Komposisi Kemasan HNAapotekerNo ratings yet
- Book PDFDocument19 pagesBook PDFAnjali KumarNo ratings yet
- CPP - Balancing EquationsDocument6 pagesCPP - Balancing EquationsAarchi SinghNo ratings yet
- Eco 101 Chap 1Document8 pagesEco 101 Chap 1rezsxNo ratings yet
- Term Paper: FIN 101 Basic FinanceDocument3 pagesTerm Paper: FIN 101 Basic FinanceErfan TanhaeiNo ratings yet
- Typing NotesDocument6 pagesTyping NotesMuhammad Ali SaqibNo ratings yet
- Maasai Mara University.: Food Crops Research Institute Kisii CentreDocument50 pagesMaasai Mara University.: Food Crops Research Institute Kisii CentreChilaNo ratings yet
- Total Station +leicaDocument17 pagesTotal Station +leicaDaro EngineerNo ratings yet
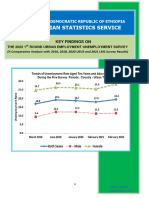
- 2022 - 1st Round UEUS Key FindingsDocument17 pages2022 - 1st Round UEUS Key FindingsEyobNo ratings yet
- Before The Book LibraryDocument433 pagesBefore The Book LibraryGreyci LinsNo ratings yet
- Chapter Four: Measures of Dispersion (Variation) : AbebuabebawDocument21 pagesChapter Four: Measures of Dispersion (Variation) : AbebuabebawYohannis RetaNo ratings yet
- Igloo Keep People WarmDocument1 pageIgloo Keep People Warmjasmine8321No ratings yet
- Haemnatopoiesis and CMLDocument8 pagesHaemnatopoiesis and CMLKe XuNo ratings yet
- Mann+Hummel: Filtration Solutions For CompressorsDocument8 pagesMann+Hummel: Filtration Solutions For CompressorsSethuraman Kumarappan (KPCL)No ratings yet
- Relationship Between Emotional Intelligence and Students Academic Performance - Role of Ethnic FactorDocument13 pagesRelationship Between Emotional Intelligence and Students Academic Performance - Role of Ethnic Factorمعن الفاعوريNo ratings yet
- CBSE Class 7 Computer Science Question Paper Set A - 0Document2 pagesCBSE Class 7 Computer Science Question Paper Set A - 0Rajesh Kumar.RNo ratings yet
- Kvs Ro JPR Class10th Science Study Material 2023-24Document98 pagesKvs Ro JPR Class10th Science Study Material 2023-24Avinesh MeenaNo ratings yet
- Medical Application Form (New) - V3-2021!10!12 - RAKDocument3 pagesMedical Application Form (New) - V3-2021!10!12 - RAKAnkita NiravNo ratings yet