MODULE 2: EXPLORING THE PRABOLAS

Learning Targets
At the end of this chapter, the students are expected to:
1. define parabola as a conic section;
2. determine the standard form and general form of equation of a parabola;
3. transform the standard from of equation into general for, and vice versa;
4. graph parabolas in a rectangular coordinate system; and
5. solve situational problems involving parabola.

Understanding the General and Standard Equations of a Parabola

A. The general form of the equation is where D, E, and F are constants:

1. y 2 + Dx+ Ey + F=0 2. x 2+ Dx+ Ey+ F=0
Example: y 2−4 x +6 y +17=0 Example: x 2+ 6 x−12 y+ 21=0

B. The standard form or the vertex form of the equation is where h and k are the coordinates of
the vertex, and P is the length of the focus.
2
1. ( y−k ) =4 p(x−h) 3. y 2=± 4 px
Example: ( y−3 )2=4 ( x−2 ) Example: y 2=16 x

2
2. ( x−h ) =4 p ( y−k ) 4. x 2=± 4 py
Example: ( x +5 ) =−8 ( y−1) Example: x 2=−56 y
2

Transforming the Equations of a Parabola from the General Form to Standard Form

It is very essential to learn how to transform a general form of equation to its standard form,
especially in cases of graphing a curve on the rectangular coordinate system. Below are the suggested
steps when changing the equation of a parabola from general form to standard form.

Steps:
1. Group the terms with same variables.
2. Move the remaining terms to the right side of the equation.
3. Create a perfect square trinomial by completing the squares. Whatever terms you have added
to the left side should also be added to the right side to keep the equation true.
4. Simplify both sides of the equation.
5. Express the perfect square trinomials as square of binomials to make the equation in the
vertex form.
Example:
Express each equation of the parabola in standard form.
1. y 2−4 x−12 y +28=0 3. 2 y 2+ 12 y −x+14=0 5. 3 y 2−24 x=0
2. x 2−2 x−4 y+ 13=0 4. 5 y 2 +30 y+ 24 x=51

Transforming the Equations of a Parabola from the Standard Form to General Form

When transforming a general form of equation to standard from, use the completing the square
method. It means that you have to reverse the process when you changed the equation from standard
form to general form. The steps are enumerated below.
1. Square the binomial and expand.
2. Place all the terms to the left side of the equation.
3. Simplify the equation by combining all like terms.
4. Write the equation in general form: x 2+ Dx+ Ey+ F=0 or y 2 + Dx+ Ey + F=0.

Example:
Express each equation of the parabola in standard form.
2 24
3. ( y +3 ) = ( x−4 )
2 2
1. ( y +5 ) =−2( x−7) 5. ( y−2 ) =−24 x−48
5
2
2. x =3( y−1) 4. ( x +5 ) =6 ( y−3)
2

1|PRECALCULUS, 1st Semester, AY 2023-2024 MSU-Binidayan CHS

 Parts and Characteristics of a Parabola

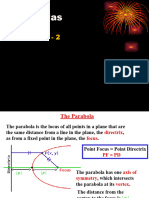
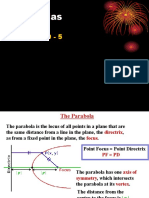
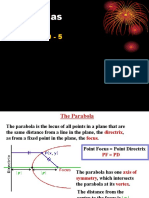
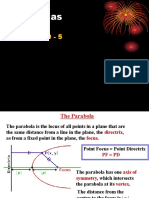
A parabola is the set of all points in a plane that are

equidistant from a fixed line called directrix and fixed point
called its focus. It has four possible openings – upward,
downward, to the right, and to the left. The line that passes
through the focus and is perpendicular to the directrix is
called the axis of symmetry, while the point where the
patabola intersects with its axis of symmetry is called the
vertex. It is the point midway between the latus rectum and
the directrix. To determine the width of the parabola’s
opening, we find/determine the length of its latus rectum.
Latus rectum is the line segment that passes through the
focus of a parabola and is perpendicular to the axis of
symmetry. It is also sometimes called the focal width.

The characteristics of parabola with vertex at (0 , 0) are summarized below:

Parabola with horizontal axis of Parabola with vertical axis of

Vertex: (0 , 0)
symmetry symmetry
Equation 2
y =4 px
2
x =4 py
Focus ( p , 0) (0 , p)
If p<0 , parabola opens to the left. If p<0 , parabola opens downward.
Opening of Parabola
If p>0 , parabola opens to the right. If p>0 , parabola opens upward.
Equation: x=± p Equation: y=± p
Direction: Vertical Direction: Horizontal
Latus Rectum
Length: 4 p Length: 4 p
Endpoints: ( p , ±2 p) Endpoints: (± 2 p , p)
Equation: y=k ; k=0 Equation: x=h ; h=0
Axis of Symmetry
Direction: Horizontal Direction: Vertical
Equation: x=− p Equation: y=− p
Directrix
Direction: Vertical Direction: Horizontal

Example:
Find the coordinates of the focus and the equation of the directrix for each parabola. Draw the
parabola, its focus and directrix.
1. x 2=20 y 3. y 2=−16 x 5. y 2=32 x
2. x 2− y=0 4. 2 x 2+5 y=0

For parabola with vertex at (h , k ), the following characteristics can be derived.

Parabola with horizontal axis of Parabola with vertical axis of

Vertex: (h , k )
symmetry symmetry
Equation ( y−k )2=4 p(x−h) 2
x =4 py
Focus (h+ p , k ) (h , k + p)
If p<0 , parabola opens to the left. If p<0 , parabola opens downward.
Opening of Parabola
If p>0 , parabola opens to the right. If p>0 , parabola opens upward.
Equation: x=h+ p Equation: y=k + p
Direction: Vertical Direction: Horizontal
Latus Rectum
Length: 4 p Length: 4 p
Endpoints: (h+ p , k ± 2 p) Endpoints: (h ± 2 p , k + p)
Equation: y=k Equation: x=h
Axis of Symmetry
Direction: Horizontal Direction: Vertical
Directrix Equation: x=h− p Equation: y=k− p

2|PRECALCULUS, 1st Semester, AY 2023-2024 MSU-Binidayan CHS

 Direction: Vertical Direction: Horizontal

Example:
2
1. ( y +3 ) =4 (x−2) 3. ( x−2 ) =8 y+ 8 5. x 2−6 x−12 y +21=0
2

2. y 2−12 y−4 x +28=0 4. ( y−2 ) =−8 x

2

Finding the Equation of a Parabola, Given Certain Conditions

Study the following examples on how you can find the equations of a parabola, given its vertex,
focal length, axis of symmetry, and opening.

Example 1. Write the standard form of equation of a parabola whose vertex is at the origin, has a
focal length of 5, has a horizontal axis of symmetry, and opens to the right.

Example 2. Find the general form of equation of a parabola whose vertex is at the origin, has a
focal length of 7, has a vertical axis of symmetry, and opens downward.

Example 3. Write the equation of a parabola whose vertex is at (2, 3) and has a directrix at x=5 .

Example 4. Write the standard form of equation of a parabola whose vertex is at the origin, has a
focal length width of 16 units, and has a directrix at x=−4 .

Example 5. Find the general form of equation of a parabola whose vertex is at (5, -1), has a focal
width of 12 units, and has a directrix at y=2.

3|PRECALCULUS, 1st Semester, AY 2023-2024 MSU-Binidayan CHS