Parabola Week 2

Content Standards
The learners demonstrate an understanding of key concepts of conic sections and systems of
nonlinear equations
Performance Standards
The learner shall be able to model situations appropriately and solve problems accurately
using conic sections and systems of nonlinear equations
Most Essential Learning Competencies
The learners define a parabola and graph a parabola given an equation in vertex form
Lesson Presentation
Parabola
1. Definition and Equation of a Parabola
2. More Properties of Parabolas
3. Situational Problems Involving Parabolas
Introduction

A parabola is one of the conic sections. We have already seen parabolas which open upward or
downward, as graphs of quadratic functions. Here, we will see parabolas opening to the left or right.
Applications of parabolas are presented at the end. 1.2.1.

Do you know that the parabola is used in the design of car headlights and in spotlights? This is because
a parabolic reflector has the property that if a light source is placed at the focus of the reflector has the
property that a light source is placed at the focus of the reflector, the light rays will reflect from the mirror as
rays parallel to the axis.
For this reason, this is used in car headlights to give an intense concentrated beam of light.

Pre - Calculus Page 1 of 9

Parabola Week 2

1.2.1 Definition and Equation of a Parabola

A parabola is the set of all points (x, y) in a plane that are equidistant from a fixed line, called the
directrix, and a fixed point called the focus, not on the line. The vertex is the midpoint between the focus and
the directrix, while the axis of symmetry of the parabola is the line passing through the focus and the vertex.
Latus Rectum is connecting two points of parabola and passes through the focus.

Degenerate Case of a Parabola

This is the case in which p = 0 yields the degenerate case (x − h) 2 = 0 or (y − k) 2 = 0 forming either the vertical
line x = h or the horizontal line y = k. This implies that degeneracy in the case of parabolas yields vertical or
horizontal lines.

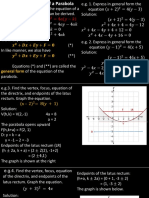
Standard Equation of a Parabola

Standard Equation Vertex at Focus Directrix Axis of Symmetry Opening of the Graph
(h,k)
2
(x – h) = 4p (y – k) (h, k + p) y=k–p x=h Upward
(x – h)2 = – 4p (y – k) (h, k – p ) y=k+p x=h Downward
(y – k)2 = 4p (x – h) (h + p,k) x=h–p y=h Right
(y – k)2 = – 4p (x – h) (h – p, k ) x=h+p y=h Left

UPWARD RIGHT

Pre - Calculus Page 2 of 9

Parabola Week 2

DOWNWARD LEFT
Conceptualizing Eccentricity
From the definition of a parabola, the distance from any point on the parabola to the focus is equal to the
distance from that same point to the directrix. Therefore, by definition, the eccentricity of a parabola must be
1.

Example 1.2.1. Determine the focus and directrix of the parabola with the given equation. Sketch the graph,
and indicate the focus, directrix, vertex, and axis of symmetry.

Pre - Calculus Page 3 of 9

Parabola Week 2

Given: x2 = 12y
The equation of parabola that opens UPWARD is (x − h) 2 = 4p(y − k)

Graph:

4𝑝 12
STEP 1: Vertex: (h, k) STEP 2: 4
= 4
STEP 3: Focus: (h, k + p)
(0, 0) p=3 (0, 0 + 3)
(0, 3)

STEP 4: Directrix: y = k − p STEP 5: Axis of Symmetry: x = h STEP 6: Latus Rectum: 2p

y=0−3 x=0 2(3) = 6
y = −3

Example 1.2.3.

Given: The figure shows the graph of parabola, with only its focus and vertex indicated. Find its
standard equation. What is the directrix and its axis of symmetry?

Solution: The parabola opens to the LEFT, we use the template (y − k)2 = −4p(x − h)
Equation: (y + 4)2 = −8p(x − 5)

Graph:

Pre - Calculus Page 4 of 9

Parabola Week 2

−4𝑝 −8
STEP 1: Vertex: (h, k) STEP 2: −4
= −4
STEP 3: Focus: (h, k + p)
(5, -4) p=-2 (5 -2, -4)
(3, -4)

STEP 4: Directrix: x = h + p STEP 5: Axis of Symmetry: y = h STEP 6: Latus Rectum: 2p

x=5+2 y=5 2(2) = 4
x=7

1.2.2. More Properties of Parabolas

If the equation is given in the general form Ax2 + Cx + Dy + E = 0 (A and C are nonzero) or By 2 + Cx + Dy + E = 0
(B and C are nonzero), we can determine the standard form by completing the square in both variables.

Example 1.2.4. Transform the equation of a parabola y2 − 5x + 12y = −16 to standard form.

Solution: We complete the square on y, and move x to the other side.

y2 + 12y = 5x – 16
y2 + 12y + 36 = 5x − 16 + 36
(y + 6)2 = 5x + 20

Standard Form: (y + 6)2 = 5(x + 4)

Transforming the Equations of a Parabola from Standard Form to General Form

Example 1.2.5. Transform the equation of a parabola (y + 5)2 = −2(x − 7) to general form.

Step 1. Square the binomial and expand.

(y + 5)2 = −2(x − 7)
y2 + 10y + 25 = −2x + 14

Step 2. Place all the terms to the left side of the equation.
y2 + 10y + 25 + 2x − 14 = 0

Step 3. Simplify the equation by combining all like terms.

y2 + 10y + 2x + 25 − 14 = 0
y2 + 10y + 2x + 11 = 0

Step 4. Write the equation in general form.

y2 + 10y + 2x + 11 = 0

Therefore, the general form of the given parabola is

y2 + 10y + 2x + 11 = 0.

Pre - Calculus Page 5 of 9

Parabola Week 2

1.2.3. Situational Problems Involving Parabolas

We now solve some situational problems involving parabolas.

Example 1.2.6.

A satellite dish has a shape called a paraboloid, where each cross-section is a parabola. Since radio
signals (parallel to the axis) will bounce off the surface of the dish to the focus, the receiver should be placed at
the focus. How far should the receiver be from the vertex, if the dish is 12 ft across, and 4.5 ft deep at the
vertex?

Solution:
The second figure above shows a cross-section of the satellite dish drawn on a rectangular
coordinate system, with the vertex at the origin. From the problem, we deduce that (6, 4.5) is a
point on the parabola. We need the distance of the focus from the vertex, i.e., the value of c in x
2 = 4cy.
x2 = 4cy
(6)2 = 4c (4.5)
36 = 18c
36 18𝑐
18
= 18

c=2

Thus, the receiver should be 2 ft. away from the vertex.

Pre - Calculus Page 6 of 9

Parabola Week 2

To Do’s:
Seatwork 1: Determine the vertex, focus, directrix, and axis of symmetry of the parabola with the given
equation. Sketch the graph, and include these points and lines.

1. x2 = − 6y
2. x2 + 2x − 8y + 33 = 0
3. x2 − 6x − 4y = −1
4. y2 + 24y − 9x + 225 = 0
5. A satellite dish shaped like a paraboloid, has diameter 2.4 ft. and depth 0.9 ft. If the receiver is placed
at the focus, how far should the receiver be from the vertex?

Pre - Calculus Page 7 of 9

Parabola Week 2

Summary of Lesson

• A parabola is the set of all points (x, y) in a plane that are equidistant from a fixed line.
• Vertex (h, k) is a midpoint between the focus and directrix
• Directrix (x or y axis) is a fixed line in a parabola.
• Focus is a fixed point in a parabola.
• Axis of symmetry is a line which cuts through the middle of the parabola
• Latus Rectum is connecting two points of parabola and passes through the focus.
• Standard equation of the parabola:

Standard Equation Vertex at Focus Directrix Axis of Symmetry Opening of the Graph
(h,k)
2
(x – h) = 4p (y – k) (h, k + p) y=k–p x=h Upward
(x – h)2 = – 4p (y – k) (h, k – p ) y=k+p x=h Downward
(y – k)2 = 4p (x – h) (h + p,k) x=h–p y=h Right
(y – k)2 = – 4p (x – h) (h – p, k ) x=h+p y=h Left

• General equation of a parabola Ax2 + Cx + Dy + E = 0

• In which p = 0 yields the degenerate case (x − h) 2 = 0 or (y − k) 2 = 0 forming either the vertical line x = h
or the horizontal line y = k. This implies that degeneracy in the case of parabolas yields vertical or
horizontal lines.
• General form to standard form by completing the square in both variables.
• Standard form to general form, expand the expression using (a + b) 2 = (a2 + 2ab + b2) and set equal to
0.

References and Supplementary Materials

Books and Journals

1. Math for Engaged Learning
Author: Yvette Lim, Rizaldi Nocon, Ederlina Nocon, and Leonor Ruivivar

Pre - Calculus Page 8 of 9

Parabola Week 2

Online Instructional Videos

1. https://francisjosephcampena.weebly.com/uploads/1/7/8/6/17869691/ched_precalculus-
part1.pd

Pre - Calculus Page 9 of 9