Professional Documents
Culture Documents
08 SampMath
Uploaded by
Shaun Miles0 ratings0% found this document useful (0 votes)
8 views1 page1. The document provides a historical introduction to stochastic processes and Brownian motion. It discusses key figures like Robert Brown, Louis Bachelier, and Albert Einstein and their contributions to understanding random particle motion.
2. Einstein developed the idea that Brownian motion results in a Gaussian distribution, with variance increasing linearly over time. Bachelier also noticed properties like the Markov property of Brownian motion.
3. Formally, a stochastic process is defined as a collection of random variables indexed by time, defined on a common probability space. The challenge is developing properties like how sample paths vary over time from a fixed starting point.
Original Description:
Historical Introduction to Stochastic Processes
Original Title
08-SampMath
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Document1. The document provides a historical introduction to stochastic processes and Brownian motion. It discusses key figures like Robert Brown, Louis Bachelier, and Albert Einstein and their contributions to understanding random particle motion.
2. Einstein developed the idea that Brownian motion results in a Gaussian distribution, with variance increasing linearly over time. Bachelier also noticed properties like the Markov property of Brownian motion.
3. Formally, a stochastic process is defined as a collection of random variables indexed by time, defined on a common probability space. The challenge is developing properties like how sample paths vary over time from a fixed starting point.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
8 views1 page08 SampMath
Uploaded by
Shaun Miles1. The document provides a historical introduction to stochastic processes and Brownian motion. It discusses key figures like Robert Brown, Louis Bachelier, and Albert Einstein and their contributions to understanding random particle motion.
2. Einstein developed the idea that Brownian motion results in a Gaussian distribution, with variance increasing linearly over time. Bachelier also noticed properties like the Markov property of Brownian motion.
3. Formally, a stochastic process is defined as a collection of random variables indexed by time, defined on a common probability space. The challenge is developing properties like how sample paths vary over time from a fixed starting point.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 1
IV.24.
Stochastic Processes 647
that the word “speed” is not really appropriate.) Ein-
IV.24 Stochastic Processes stein’s method was based on considerations of statis-
Jean-François Le Gall tical physics, which led him to the heat equation
[I.3 §5.4] and then to the Gaussian density that solves
this equation (see section 5.2).
1 Historical Introduction A few years before Einstein, the French mathemati-
Stochastic processes are one of the major themes of cian Louis Bachelier, in his work about the mathemat-
modern probability theory. Roughly speaking, they are ical modeling of stock markets, had already noticed
mathematical models that describe the evolution of the Gaussian distribution of Brownian motion. How-
random phenomena as time goes by. In this article, we ever, Bachelier was dealing not with the physical phe-
shall introduce and illustrate the fundamental ideas of nomenon known as Brownian motion, but rather with
the theory of stochastic processes by concentrating on random walks where the step size was very small. As
the single most important example: Brownian motion. we shall see in sections 2 and 3, the two concepts are
essentially equivalent from a mathematical viewpoint.
We start with a brief historical introduction, in order to
Bachelier pointed out what we call today the Markov
provide some motivation for the mathematical theory
property of Brownian motion: if we wish to predict the
that follows.
displacement after time t of a Brownian particle, then
In 1828, the British botanist Robert Brown observed
knowledge of the path followed by the particle before
the very irregular and wiggly motion of small particles
time t does not help us any more than just knowing
of pollen suspended in water. Brown pointed out the
the position at time t. Bachelier’s arguments were not
unpredictable character of the motion, which appeared
completely satisfactory, and his ideas were not fully
to obey no known physical rule. During the nineteenth
appreciated in his time.
century, several physicists tried to understand the ori-
How does one go about modeling a particle that
gin of this “Brownian motion,” which turned out to
moves in a random way? A first remark is that the posi-
be present in many other physical phenomena. Several
tion of the particle at time t will be a random variable
theories were proposed, some of them rather fanci-
[III.71 §4] Bt . But these random variables will depend on
ful: perhaps Brownian particles were living microscopic
each other: if you know where the particle is at time t,
animals, or perhaps the motion was due to electro-
it will affect your knowledge of how likely it is to be in
static forces. By the end of the century, however, physi-
a certain region at some later time. These two consid-
cists had concluded that the constant changes of direc- erations can be accommodated if we take as our basic
tion in Brownian motion could be explained by the model a set of random variables Bt , one for each non-
impacts on a particle from the molecules of the sur- negative real number, all defined on the same underly-
rounding medium. If the particle was sufficiently light, ing probability space. This, formally speaking, is what
then these numerous collisions could have a macro- a stochastic process is.
scopic influence on its displacement. This explanation This may seem a rather simple definition, but in order
was also consistent with the experimental observation for a stochastic process to be interesting it needs to
that the motion became faster if the temperature of the have additional properties, and difficult mathematical
water, and thus the thermal agitation of its molecules, questions arise as soon as one tries to obtain them. Let
increased. us write Ω for the underlying probability space. Then
Albert Einstein, in one of his three famous 1905 each of the random variables Bt is a function from Ω to
papers, was responsible for a major step forward in R3 , and therefore we associate a point in R3 with each
the understanding of Brownian motion. He worked out pair (t, ω) (where t is a positive real number and ω
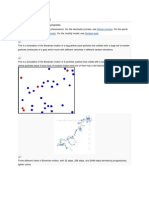
that if a Brownian particle starts at the origin, then belongs to Ω). So far we have thought about the prob-
after a fixed time t its position should be randomly dis- ability distribution of Bt , so we have been focusing on
tributed according to the (three-dimensional) gaussian what happens when we fix t and let ω vary. However,
distribution [III.71 §5] with mean 0 and variance σ 2 t, we must also consider what happens when we look at
where σ 2 is a constant, called the diffusion constant, a “single instance” of a stochastic process, by fixing ω
that measures how quickly the distribution spreads and letting t vary. For fixed ω, the function that takes t
out with time. (One can think of this loosely as the to Bt (ω) is called a sample path. If we want a rigorous
speed of the Brownian motion, but we shall see later mathematical theory of Brownian motion, then a very
You might also like
- Quantum Theory Without ObserversDocument21 pagesQuantum Theory Without ObserverscdcrossroaderNo ratings yet
- GravitationDocument16 pagesGravitationGraecus1No ratings yet
- The Patristic Doctrine of Creation by Fr. Seraphim RoseDocument46 pagesThe Patristic Doctrine of Creation by Fr. Seraphim Roseakrob100% (3)
- The Universe On A Tee ShirtDocument26 pagesThe Universe On A Tee ShirtJohn WindersNo ratings yet
- The Evolution of The UniverseDocument101 pagesThe Evolution of The UniverseNoman QureshiNo ratings yet
- Relativity PDFDocument82 pagesRelativity PDFDavidSuarez100% (3)
- Spooky PhysicsDocument44 pagesSpooky PhysicsMir MirceaNo ratings yet
- R.pearson - Key To Consciousness. Quantum GravitationDocument16 pagesR.pearson - Key To Consciousness. Quantum GravitationJorgee_Porgee_8203No ratings yet
- Probability MITDocument116 pagesProbability MITMinh Quan LENo ratings yet
- Henry Stapp - QuantumDocument35 pagesHenry Stapp - Quantummet3311100% (2)
- Brownian MotionDocument76 pagesBrownian MotionPraveen KumarNo ratings yet
- Concerning Time, Space and MusicDocument18 pagesConcerning Time, Space and MusicChrisTselentisNo ratings yet
- Wiener, N. Time, Communication, and The Nervous SystemDocument24 pagesWiener, N. Time, Communication, and The Nervous SystemRodolfo van GoodmanNo ratings yet
- Weber-Type Laws of Action-at-a-Distance in Modern PhysicsDocument18 pagesWeber-Type Laws of Action-at-a-Distance in Modern PhysicsnirvicharaaNo ratings yet
- Perform Quantitative Risk AnalysisDocument12 pagesPerform Quantitative Risk AnalysissdfasdfasdfasfaNo ratings yet
- Zarah & Pharez: Questions & AnswersDocument15 pagesZarah & Pharez: Questions & AnswersEnrique RamosNo ratings yet
- Ged 109 Reviewer General Concepts and Historical Events in Science, Technology and Society Scientific RevolutionDocument25 pagesGed 109 Reviewer General Concepts and Historical Events in Science, Technology and Society Scientific Revolutionjustine reine cornicoNo ratings yet
- Poincaré and The Special Theory of RelativityDocument4 pagesPoincaré and The Special Theory of RelativityNAYEEM_AIUBNo ratings yet
- 3rdquarter Systems Sci10 DLLDocument6 pages3rdquarter Systems Sci10 DLLkaycin DuzonNo ratings yet
- Causal InterpretationDocument5 pagesCausal InterpretationHaris_IsaNo ratings yet
- Critica A Rosenblum, KuttnerDocument23 pagesCritica A Rosenblum, KuttnerfmcapoNo ratings yet
- Free Fall - Definition, Examples, & Facts - BritannicaDocument8 pagesFree Fall - Definition, Examples, & Facts - BritannicareddygrNo ratings yet
- The Labyrinth of Quantum LogicDocument41 pagesThe Labyrinth of Quantum LogicJordan BlevinsNo ratings yet
- Brownian Motion: From Wikipedia, The Free EncyclopediaDocument21 pagesBrownian Motion: From Wikipedia, The Free EncyclopediarayroyNo ratings yet
- Karthikeya XII-A Physics Project PDFDocument23 pagesKarthikeya XII-A Physics Project PDFkarthikeya kakarlapudiNo ratings yet
- Boltzmann's Approach To Statistical MechanicsDocument16 pagesBoltzmann's Approach To Statistical MechanicsTony RossNo ratings yet
- A History of Time: 20th Century Time: Version For PrintingDocument9 pagesA History of Time: 20th Century Time: Version For PrintingKatherine WilsonNo ratings yet
- Unpredictability Uncertainty and Fractal StructureDocument5 pagesUnpredictability Uncertainty and Fractal StructureArtur MinasyanNo ratings yet
- On Wheeler's Quantum Circuit: Gregg JaegerDocument35 pagesOn Wheeler's Quantum Circuit: Gregg Jaegerabhi.chakra01No ratings yet
- 2005 Frey Brownian Motion A Paradigm of Soft Matter and Biological PhysicsDocument31 pages2005 Frey Brownian Motion A Paradigm of Soft Matter and Biological PhysicscsNo ratings yet
- MazoDocument4 pagesMazomarcoNo ratings yet
- Epistemic and Ontic Quantum RealitiesDocument22 pagesEpistemic and Ontic Quantum RealitiesJorge MoraNo ratings yet
- 2010 The Definition of Mach's PrincipleDocument22 pages2010 The Definition of Mach's PrincipleWI TONo ratings yet
- Brownian MotionDocument31 pagesBrownian Motionsujatha ramkiNo ratings yet
- Lecture 23: Decoherence and Foundations of QM (12/13/2005)Document8 pagesLecture 23: Decoherence and Foundations of QM (12/13/2005)bgiangre8372No ratings yet
- Richard Amoroso - Time$ - 6р PDFDocument6 pagesRichard Amoroso - Time$ - 6р PDFАнатолий ПодругинNo ratings yet
- Norbert Wiener - Time, Communication, and The Nervous SystemDocument24 pagesNorbert Wiener - Time, Communication, and The Nervous SystemBenjamim GomesNo ratings yet
- Quantum Theory and The Role of Mind in Nature: March 1, 2001 LBNL-44712Document42 pagesQuantum Theory and The Role of Mind in Nature: March 1, 2001 LBNL-44712EyiogbeNo ratings yet
- A 16 Unsubstantiated Relativity Models DR Burniston BrownDocument14 pagesA 16 Unsubstantiated Relativity Models DR Burniston BrownAnonymous i71HvPXNo ratings yet
- Time As An Illusion: PSW - Papers@yahoo - CaDocument21 pagesTime As An Illusion: PSW - Papers@yahoo - CaIgor CorreiaNo ratings yet
- Demonstration of The Existence of A Velocity Vector Missing From The Special Theory of RelativityDocument8 pagesDemonstration of The Existence of A Velocity Vector Missing From The Special Theory of RelativityAndre LanzerNo ratings yet
- Butterfield LeibnClarkeDocument9 pagesButterfield LeibnClarkerebe53No ratings yet
- What Is The Meaning of The Wave Function?Document20 pagesWhat Is The Meaning of The Wave Function?nNo ratings yet
- Bush Physics Today2015Document8 pagesBush Physics Today2015TomCafezNo ratings yet
- Chronos KairosDocument10 pagesChronos KairosDana Kiosa100% (1)
- Will String Theory Lead To A Reformulation of Quantum Mechanics?Document1 pageWill String Theory Lead To A Reformulation of Quantum Mechanics?Denzel WillingtonNo ratings yet
- tmpB89E TMPDocument19 pagestmpB89E TMPFrontiersNo ratings yet
- Bohmian Mechanics and Quantum Field TheoDocument4 pagesBohmian Mechanics and Quantum Field Theoroberto estradaNo ratings yet
- Basic Quantum TheoryDocument3 pagesBasic Quantum Theoryrahsan.swrNo ratings yet
- V. Christianto - On The Origin of Macroquantization in Astrophysics and Celestial MotionDocument13 pagesV. Christianto - On The Origin of Macroquantization in Astrophysics and Celestial MotionHuntsmithNo ratings yet
- 0063 0078Document16 pages0063 0078Anurag AnandNo ratings yet
- The Celestial Mechanics of Newton: Dipankar BhattacharyaDocument10 pagesThe Celestial Mechanics of Newton: Dipankar BhattacharyaAlexander AlekhineNo ratings yet
- The Clockwork Universein ChaosDocument17 pagesThe Clockwork Universein ChaosanuragkrishnaNo ratings yet
- The Animate and The Inanimate - William James SidisDocument88 pagesThe Animate and The Inanimate - William James SidisAdriano CordeiroNo ratings yet
- Penrose 2018-Big Bang and Its Dark-MatterDocument14 pagesPenrose 2018-Big Bang and Its Dark-MatterChris GolightlyNo ratings yet
- Weber-Type Laws of Action-at-a-Distance in Modern PhysicsDocument18 pagesWeber-Type Laws of Action-at-a-Distance in Modern PhysicsEdel PonsNo ratings yet
- Bush PHYSICS TODAY2015 PDFDocument9 pagesBush PHYSICS TODAY2015 PDFAyussh VoltegourdeNo ratings yet
- Brownian MotionDocument25 pagesBrownian Motionsujatha ramkiNo ratings yet
- Culture of Quantum ChaosDocument21 pagesCulture of Quantum Chaosvaleria seminarioNo ratings yet
- Explaining Michelson-Morley Without Spec PDFDocument3 pagesExplaining Michelson-Morley Without Spec PDFAndré AbramczukNo ratings yet
- Newton - de GravitationeDocument4 pagesNewton - de GravitationeOmar KassemNo ratings yet
- Chairperson Inventory.2024Document4 pagesChairperson Inventory.2024Shaun MilesNo ratings yet
- The Phys MicroDocument3 pagesThe Phys MicroShaun MilesNo ratings yet
- 10 SampMathDocument1 page10 SampMathShaun MilesNo ratings yet
- 05 SampMathDocument1 page05 SampMathShaun MilesNo ratings yet
- 04 SampMathDocument1 page04 SampMathShaun MilesNo ratings yet
- 07 SampMathDocument1 page07 SampMathShaun MilesNo ratings yet
- SU Figure 4: Macro Processor - Output ProcessingDocument1 pageSU Figure 4: Macro Processor - Output ProcessingShaun MilesNo ratings yet
- 01 SampMathDocument2 pages01 SampMathShaun MilesNo ratings yet
- 00 SampMathDocument2 pages00 SampMathShaun MilesNo ratings yet
- Figure 5: Macro Result Pushed Back Onto StackDocument1 pageFigure 5: Macro Result Pushed Back Onto StackShaun MilesNo ratings yet
- PG 03Document1 pagePG 03Shaun MilesNo ratings yet
- Catdvi File - Dvi - TR - S " /T" "/N" - Fgrep 'XXX (' - Sort - U A Sectional Unit Is A Part, Chapter, Section, Subsection, EtcDocument1 pageCatdvi File - Dvi - TR - S " /T" "/N" - Fgrep 'XXX (' - Sort - U A Sectional Unit Is A Part, Chapter, Section, Subsection, EtcShaun MilesNo ratings yet
- Jurnal RossilawatiDocument13 pagesJurnal RossilawatiراسیلاواتیNo ratings yet
- CH 1 MCQs KEYDocument12 pagesCH 1 MCQs KEYmazmaz1212No ratings yet
- Heideggers Ideas About DeathDocument6 pagesHeideggers Ideas About DeathCristian TayagNo ratings yet
- Full Download Test Bank For Chemistry 9th Edition Zumdahl Isbn 10 1133611095 Isbn 13 9781133611097 PDF Full ChapterDocument36 pagesFull Download Test Bank For Chemistry 9th Edition Zumdahl Isbn 10 1133611095 Isbn 13 9781133611097 PDF Full Chapterpoliture.caprylicnth9x100% (19)
- Some of The Fellowship Details in INDIADocument23 pagesSome of The Fellowship Details in INDIASaurav DasNo ratings yet
- MBA Project TOCDocument3 pagesMBA Project TOCKasubabu YajjalaNo ratings yet
- CV Tegar PrajaksaDocument6 pagesCV Tegar Prajaksaijejejerry100% (1)
- EDA 11 Introduction To Lesson 6Document38 pagesEDA 11 Introduction To Lesson 6John David LoberosNo ratings yet
- P Resident Ramon Magsaysay State University Iba, Zambales: Graduate School Ma 210 - Research MethodologyDocument4 pagesP Resident Ramon Magsaysay State University Iba, Zambales: Graduate School Ma 210 - Research MethodologyRodrick Sonajo RamosNo ratings yet
- q1 Week 7Document29 pagesq1 Week 7IsraelDelMundoNo ratings yet
- Case Study T 10Document5 pagesCase Study T 10zinaida casianuNo ratings yet
- NEERI Journal DetailsDocument4 pagesNEERI Journal DetailsSubhashree Mishra0% (1)
- EE Guide - Physics v1Document41 pagesEE Guide - Physics v1gaminglabelNo ratings yet
- Nature of PhilosophyDocument2 pagesNature of PhilosophyBSN CMUNo ratings yet
- Model Building and Deficition of Science GILBERT 1991Document7 pagesModel Building and Deficition of Science GILBERT 1991anaNo ratings yet
- Stazione Zoologica Anton Dohrn - Napoli History and Philosophy of The Life SciencesDocument24 pagesStazione Zoologica Anton Dohrn - Napoli History and Philosophy of The Life SciencesArctic OneNo ratings yet
- Chapter 1 Lesson 3 - Quantitative and Qualitative ResearchDocument12 pagesChapter 1 Lesson 3 - Quantitative and Qualitative ResearchRomeo LicarteNo ratings yet
- Walnut Hill School For The Arts Math Algebra 1 Placement TestDocument6 pagesWalnut Hill School For The Arts Math Algebra 1 Placement TestSUNGMIN CHOINo ratings yet
- Sakina CVDocument1 pageSakina CVapi-357133617No ratings yet
- Research Methodology Masters Dec 2017Document55 pagesResearch Methodology Masters Dec 2017Aiman OmerNo ratings yet
- Predictors of Student's Performance in TIMSS Mathematics Released ItemsDocument8 pagesPredictors of Student's Performance in TIMSS Mathematics Released ItemsPsychology and Education: A Multidisciplinary JournalNo ratings yet
- Feser - Classical Natural Law Theory Property Rights and TaxationDocument32 pagesFeser - Classical Natural Law Theory Property Rights and TaxationCharles Walter100% (1)
- Symbolic Interaction Theory: Nilgun Aksan, Buket Kısac, Mufit Aydın, Sumeyra DemirbukenDocument3 pagesSymbolic Interaction Theory: Nilgun Aksan, Buket Kısac, Mufit Aydın, Sumeyra DemirbukenIgor Dutra BaptistaNo ratings yet
- Reason of Grade 12 HUMSS 10 Choosing Their StrandDocument4 pagesReason of Grade 12 HUMSS 10 Choosing Their Strandchristian bill malagyabNo ratings yet