Week I: Kinematics of Particles: Hakan Dogan

Week I: Kinematics of Particles
Hakan Dogan
Department of Mechanical Engineering

Hacettepe University
MMU 204 - Dynamics

23-24 Spring
Acknowledgement: These lecture slides are almost completely same as

Prof Dr Engin Tanik’s and Prof Dr Volkan Parlaktas’s previous Dynamics lecture
slides.
Hakan Dogan MMU204 Dynamics February 22, 2024 1 / 36

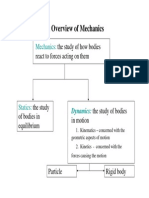
Kinematics of Particles Introduction
Kinematics of Particles
Sections:
Rectilinear motion
Plane curvilinear motion
Rectangular coordinates (x − y )
Normal and tangential coordinates (n − t)
Polar coordinates (r − θ )
Space curvilinear motion
Relative motion (Translating axes)
Constrained motion of connected particles

Choose of Coordinates
Question: How to describe the position of particle P at any time t?


Rectangular coordinates (x, y , z)

Cylindrical coordinates (r , θ , z)

Spherical coordinates (R, θ , φ )

Spherical coordinates (R, θ , φ )
Normal-tangent coordinates (n, t)

Kinematics of Particles Rectilinear Motion
Rectilinear Motion
Consider a particle P moving along a straight line. The position of P at
any instant of time t can be specified by its distance s measured from
some convenient reference point O fixed on the line. At time t + ∆t the
particle has moved to P ′ and its coordinate becomes s + ∆s. The change
in the position coordinate during the interval ∆t is called the displacement
∆s of the particle. The displacement would be negative if the particle
moved in the negative s-direction.

Velocity
The average velocity of the particle during the interval ∆t is the
displacement divided by the time interval or vav = ∆s/∆t. As ∆t
becomes smaller and approaches zero in the limit, the average velocity
approaches the instantaneous velocity of the particle, which is
∆s ds
v = lim or v= = ṡ
∆t→0 ∆t dt

Acceleration
The average acceleration of the particle during the interval ∆t is the
change in its velocity divided by the time interval or aav = ∆v /∆t. As ∆t
becomes smaller and approaches zero in the limit, the average acceleration
approaches the instantaneous acceleration of the particle, which is
∆v
a = lim
∆t→0 ∆t
dv d 2s
a= = v̇ or a= = s̈
dt dt 2

Velocity and Acceleration (contd.)
By eliminating the time dt between the equations given below,

ds
v= = ṡ
dt
dv
a= = v̇
dt
we obtain a differential equation relating displacement, velocity, and
acceleration. This equation is
vdv = ads or ṡd ṡ = s̈ds

Analytical Integration
When a is constant , equations a = dv /dt = v̇ and vdv = ads can be

integrated directly. For simplicity withs = s0 , v = v0 and t = 0
designated at the beginning of the interval, then for a time interval t
the integrated equations become
Z v Z t
dv = a dt or v = v0 + at
v0 0
Z v Z s
vdv = a ds or v 2 = v02 + 2a(s − s0 )
v0 s0
CAUTION: The above equations have been integrated for constant

acceleration only. A common mistake is to use these equations for
problems involving variable acceleration, where they do not apply.

Analytical Integration
Substitution of the integrated expression for v into equation

v = ds/dt = ṡ and integration with respect to t give
Z s Z t
1
ds = (v0 + at)dt or s = s0 + v0 t + at 2
s0 0 2
CAUTION: The above equations have been integrated for constant
acceleration only. A common mistake is to use these equations for
problems involving variable acceleration, where they do not apply.

Sample Problem #1
The position coordinate of a particle which is confined to move along a

straight line is given by s = 2t 3 − 24t + 6, where s is measured in meters
from a convenient origin and t is in seconds. Determine
A The time required for the particle to reach a velocity of 72 m/s from
its initial condition at t = 0,
B The acceleration of the particle when v = 40 m/s, and
C The net displacement of the particle during the interval from t = 1 s
to t = 4 s.

Solution #1

Sample Problem #2
When the effect of aerodynamic drag is included, the y -acceleration of a
baseball moving vertically upward is au = −g − kv 2 , while the acceleration
when the ball is moving downward is ad = −g + kv 2 . If the ball is thrown
upward at 30 m/s from essentially ground level, compute its maximum
height h and its speed vf upon impact with the ground. Take k to be
0.006 m−1 and assume that g is constant.

Kinematics of Particles Plane curvilinear motion
Plane curvilinear motion

Consider now the continuous motion of a particle along a plane curve as
represented in Figure. At time t the particle is at position A, which is
located by the position vector r measured from some convenient fixed
origin O. If both the magnitude and direction of r are known at time t,
then the position of the particle is completely specified. At time t + ∆t,
the particle is at A′ , located by the position vector r + ∆r.

Plane curvilinear motion (contd.) - Velocity
We now extend the basic definition of the derivative of a scalar

quantity to include a vector quantity and write
dr
v= = ṙ
dt
The derivative of a vector is itself a vector having both magnitude and
a direction. The magnitude of v is called the speed and is the scalar
ds
v = |v| = = ṡ
dt

Plane curvilinear motion - Acceleration
The average acceleration of the particle between A and A′ is defined

as ∆v/∆t, which is a vector whose direction is that of ∆v divided by
∆t.
The instantaneous acceleration a of the particle is defined as the
limiting value of the average acceleration as the time interval
approaches zero. Thus,
∆v
a = lim
∆t→0 ∆t
By definition of the derivative, then, we write

dv
a= = v̇
dt

Plan curvilinear motion - Visualisation of Motion

Rectangular coordinates - Vector representation

This system of coordinates is particularly useful for describing motions
where the x- and y -components of acceleration are independently
generated or determined.

Sample Problem #3
A rocket has expended all its fuel when it reaches position A, where it has
a velocity u at an angle θ with respect to the horizontal. It then begins
unpowered flight and attains a maximum added height h at position B
after travelling a horizontal distance s from A to B. Determine the
expressions for h and s, the time t of flight from A to B, and the equation
of the path. For the interval concerned, assume a flat earth with a
constant gravitational acceleration g and neglect atmospheric resistance.

Sample Problem #3

Normal and tangential coordinates (n − t)

The n- and t-coordinates are considered to move along the path with the
particle as seen in Figure where the particle advances from A to B to C .

Normal and tangential coordinates (n − t) - Velocity

The magnitude of the velocity can be written v = ds/dt = ρ β˙ /dt, and we
can write the velocity as the vector:
v = v et = ρ β˙ et

Normal and tangential coordinates (n − t) - Acceleration
The acceleration a of the particle is defined as,
dv d(v et )
a= = = v e˙t + v̇ et
dt dt
e˙t = β˙ en
v2
a= en + v̇ et
ρ
v2
an = = ρ β˙ 2 = v β˙ and at = v̇ = s̈
ρ
q
a = an2 + at2

Normal and tangential coordinates (n − t) - Geometric

interpretation
It is especially important to observe that the normal component of

acceleration an is always directed toward the center of curvature C .

Normal and tangential coordinates (n − t) - Circular

motion
v = r θ̇
v2
an = = r θ̇ 2 = v θ̇
r
at = v̇ = r θ̈

Sample Problem #4
To anticipate the dip and hump in the road, the driver of a car applies her
brakes to produce a uniform deceleration. Her speed is 100 km/h at the
bottom A of the dip and 50 km/h at the top C of the hump, which is 120
m along the road from A. If the passengers experience a total acceleration
of 3 m/s2 at A and if the radius of curvature of the hump at C is 150 m,
calculate
A the radius of curvature at A,
B the acceleration at the inflection point B, and
C the total acceleration at C .

Sample Problem #4

Sample Problem #5
A football player releases a ball with the initial conditions shown in the
figure. Determine the radius of curvature of the trajectory
A just after release and
B at the apex.
For each case, compute the time rate of change of the speed

Polar coordinates (r − θ )
The particle is located by the radial distance r from a fixed point and by
an angular measurement θ to the radial line. Polar coordinates are
particularly useful when a motion is constrained through the control of a
radial distance and an angular position or when an unconstrained motion
is observed by measurements of a radial distance and an angular position.
r = r er

Polar coordinates (r − θ ) - Velocity
v = ṙ = r˙er + r e˙r
v = r˙er + r θ̇ eθ
vr = r˙ and vθ = r θ̇
q
v = vr2 + vθ2

Polar coordinates (r − θ ) - Acceleration

a = v̇ = (¨
r er + r˙e˙r ) + (r˙θ̇ eθ + r θ̈ eθ + r θ̇ e˙θ )
r − r θ̇ 2 )er + (r θ̈ + 2r˙θ̇ )eθ
a = (¨
ar = r¨ − r θ̇ 2 and aθ = r θ̈ + 2r˙θ̇
q
a = ar2 + aθ2

Polar coordinates (r − θ ) - Circular motion

For motion in a circular path with r constant, the equations in polar
coordinates become simply
Velocity:
vr = 0 and vθ = r θ̇
Acceleration:
ar = −r θ̇ 2 and aθ = r θ̈

Sample Problem #6
Rotation of the radially slotted arm is governed by θ = 0.2t + 0.02t 3 ,
where θ is in radians and t is in seconds. Simultaneously, the power screw
in the arm engages the slider B and controls its distance from O according
to r = 0.2 + 0.04t 2 , where r is in meters and t is in seconds. Calculate the
magnitudes of the velocity and acceleration of the slider for the instant
when t = 3 s.

Sample Problem #6

Sample Problem #7
The piston of the hydraulic cylinder gives pin A a constant velocity
v = 1.5 m/s in the direction shown for an interval of its motion. For the
instant when θ = 60◦ , determine r˙, r¨, θ̇ , and θ̈ where r = OA.

Sample Problem #6

Next Lecture
Space curvilinear motion

Relative motion
Constrained motion of connected particles
Review of Chapter 2

Week I: Kinematics of Particles: Hakan Dogan

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Week I: Kinematics of Particles: Hakan Dogan

Uploaded by

Copyright:

Available Formats

Week I: Kinematics of Particles

Department of Mechanical Engineering

MMU 204 - Dynamics

Acknowledgement: These lecture slides are almost completely same as

Hakan Dogan MMU204 Dynamics February 22, 2024 1 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 2 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 3 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 3 / 36

Rectangular coordinates (x, y , z)

Hakan Dogan MMU204 Dynamics February 22, 2024 3 / 36

Rectangular coordinates (x, y , z)

Hakan Dogan MMU204 Dynamics February 22, 2024 3 / 36

Rectangular coordinates (x, y , z)

Spherical coordinates (R, θ , φ )

Hakan Dogan MMU204 Dynamics February 22, 2024 3 / 36

Rectangular coordinates (x, y , z)

Spherical coordinates (R, θ , φ )

Normal-tangent coordinates (n, t)

Hakan Dogan MMU204 Dynamics February 22, 2024 3 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 4 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 5 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 6 / 36

Velocity and Acceleration (contd.)

By eliminating the time dt between the equations given below,

vdv = ads or ṡd ṡ = s̈ds

Hakan Dogan MMU204 Dynamics February 22, 2024 7 / 36

When a is constant , equations a = dv /dt = v̇ and vdv = ads can be

CAUTION: The above equations have been integrated for constant

Hakan Dogan MMU204 Dynamics February 22, 2024 8 / 36

Substitution of the integrated expression for v into equation

Hakan Dogan MMU204 Dynamics February 22, 2024 9 / 36

The position coordinate of a particle which is confined to move along a

Hakan Dogan MMU204 Dynamics February 22, 2024 10 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 11 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 12 / 36

Plane curvilinear motion

Hakan Dogan MMU204 Dynamics February 22, 2024 13 / 36

Plane curvilinear motion (contd.) - Velocity

We now extend the basic definition of the derivative of a scalar

Hakan Dogan MMU204 Dynamics February 22, 2024 14 / 36

Plane curvilinear motion - Acceleration

The average acceleration of the particle between A and A′ is defined

By definition of the derivative, then, we write

Hakan Dogan MMU204 Dynamics February 22, 2024 15 / 36

Plan curvilinear motion - Visualisation of Motion

Hakan Dogan MMU204 Dynamics February 22, 2024 16 / 36

Rectangular coordinates - Vector representation

Hakan Dogan MMU204 Dynamics February 22, 2024 17 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 18 / 36

Hakan Dogan MMU204 Dynamics February 22, 2024 19 / 36

Normal and tangential coordinates (n − t)

Hakan Dogan MMU204 Dynamics February 22, 2024 20 / 36

Normal and tangential coordinates (n − t) - Velocity

Hakan Dogan MMU204 Dynamics February 22, 2024 21 / 36

Normal and tangential coordinates (n − t) - Acceleration

The acceleration a of the particle is defined as,

Hakan Dogan MMU204 Dynamics February 22, 2024 22 / 36

Normal and tangential coordinates (n − t) - Geometric

It is especially important to observe that the normal component of

Hakan Dogan MMU204 Dynamics February 22, 2024 23 / 36

Normal and tangential coordinates (n − t) - Circular

Hakan Dogan MMU204 Dynamics February 22, 2024 24 / 36

Rectangular coordinates (x, y , z)

Rectangular coordinates (x, y , z)

Rectangular coordinates (x, y , z)

Spherical coordinates (R, θ , φ )

Rectangular coordinates (x, y , z)

Spherical coordinates (R, θ , φ )

Normal-tangent coordinates (n, t)

The average acceleration of the particle between A and A′ is defined

Space curvilinear motion