REAL NUMBERS 20.
144 cartons of Coke cans and 90 cartons of Pepsi cans
4-MARKS & 3-MARKS
1. For any positive integer n, prove that n3 − n is
divisible by 6.
2. Prove that √ 3 is an irrational number. Hence, show that
7 + 2√ 3 is also an irrational number.
3. Find HCF of 81 and 237 and express it as a linear
combination of 81 and 237 i.e. given that
HCF(81,237)=81x + 237y for some x and y .
4. Show that the square of any positive integer is of the
forms 4m or 4m + 1, where m is any integer.
5. Express the HCF&LCM of 48 & 18 as a linear
combination.
6. Find the HCF of 256 and 36 using Euclid’s Division
Algorithm. Also, find their LCM and verify result
HCF × LCM = Product of the two numbers.
7. A sweet seller has 420 kaju barfis and 130 badam barfis.
She wants to stack them in such a way that each stack
has the same number, and they take up the least area of
the tray. What is the number of that can be placed in
each stack for this purpose?
8. Use Euclid’s division lemma to show that the cube of any
positive integer is of the form 9m, 9m + 1 or 9m + 8.
9. Use Euclid’s division lemma to show that the square of
any positive integer is either of the form 3m or 3m + 1
for some integer m
10. Show that any positive odd integer is of the form 6q +
1, or 6q + 3, or 6q + 5, where q is some integer
11. Use Euclid’s division algorithm, find the HCF (867,255)
12. Find the HCF of 96 and 404 by the prime factorizations
method. Hence, find their LCM.
13. Use Euclid’s algorithm to find the HCF(4052, 12576)
14. Find HCF and LCM of 378, 180 and 420 by prime
factorization method. Is HCF × LCM of these numbers
equal to the product of the given three numbers?
15. If two positive integers a and b are written as a = x 3y2 &
b = xy3 ; x, y are prime numbers, find the HCF (a, b) ?
16. A circular field has a circumference of 360 km. Three
cyclists start together and can cycle 48, 60 & 72 km a
day, round the field. When will they meet again?
17. Show that cube of any positive integer is of the form
4m, 4m + 1 or 4m + 3, for some integer m.
18. An army contingent of 616 members is to march
behind an army band of 32 members in a parade. The
two groups are to march in the same number of
columns. What is the maximum number of columns in
which they can march?
19. Find the HCF and LCM of 6, 72 and 120, using the prime
factorizations method.
are to be stacked in a canteen. If each stack is of the
same height and if it equal contain cartons of the same
drink, what would be the greatest number of cartons
each stack would have?
21. Find the HCF and LCM of 510 and 92 and verify that
HCF × LCM = Product of two given numbers.
22. Three bells toll at intervals of 9, 12, 15 minutes
respectively. If they start tolling together, after what
time will they next toll together?
23. Given that HCF (306, 1314) = 18. Find LCM (306,
1314)
24. Find HCF and LCM of 16 and 36 by prime factorization
and check your answer.
25. Find the HCF, by Euclid’s division algorithm of the
numbers 92690, 7378 and 7161.
26. Use Euclid division lemma to show that the square of
any positive integer cannot be of the form 5m + 2 or
5m + 3 for some integer m.
27. Find the HCF of 180, 252 and 324 by Euclid’s Division
algorithm.
----------------------------------------------------------------------
POLYNOMIALS
4-MARKS & 3-MARKS
1. Obtain all other zeroes of the polynomial
x4+ 6x3+ x2− 24x − 20, if two of its zeroes are 2 &−5.
2. Obtain all other zeroes of the polynomial
4x4+ x3− 72x2− 18x , if its 2 zeroes are 3√ 2 & −3√ 2 .
3. Obtain all other zeroes of the polynomial
9x4− 6x3− 35x2+ 24x − 4, if 2 of its zeroes are 2 &−2.
4. If the polynomial x4− 6x3+ 16x2− 25x + 10 is divided by
(x2− 2x + k), the remainder comes out to be x + a, find
k and a.
5. If the polynomial 6𝑥4 + 8𝑥3 − 5𝑥2 + 𝑎𝑥 + 𝑏 is exactly
2
divisible by the polynomial 2𝑥 − 5, then find the
value of 𝑎 and 𝑏.
6. Find all zeroes of the polynomial
(2x4 – 9x3 + 5x2 + 3x – 1) if two of its zeroes are
(2 + √3) and (2 – √3).
7. Obtain all the zeroes of x4- 7x3 +17x2-17x + 6 , if two of
its zeroes are 3 and 1.
8. Show that 3 is a zero of the polynomial 2x3− x2− 13x −
6. Hence find all the zeroes of this polynomial.
9. Given that x − √ 5 is a factor of the polynomial
x3− 3√ 5 x2− 5x + 15√ 5 , find all the zeroes of the
polynomial.
10. Find the other zeroes of the polynomial x4− 5x3+ 2x2+
10x − 8 if it's two zeroes are − √ 2 and √ 2.
11. What should be added to x3+ 5x2+ 7x + 3 so that it is
completely divisible by x2+ 2x .
12. Obtain all other zeroes of 3x4+6x3-2x2-10x-5, if two of
its zeroes are
√ 3 √
5 and - 5
3
13. Check whether the polynomial t2– 3 is a factor of
Polynomial 2t4 + 3t3 – 2t2 –9t – 12.
14. If one the zero of a polynomial 3x2− 8x + 2k + 1 is
seven times the other, find the value of k.
1 if its speed were 5 km/h more. Find the original speed
15. Verify whether 2, 3 and are the zeroes of the
2
polynomial p(x) = 2x3− 11x2+ 17x − 6.
16. If the sum and product of the zeroes of the polynomial
ax2− 5x + c are equal to10 each, find values of 'a '& 'c'.
17. If one root of the quadratic equation 6x2− x − k = 0 is
3
, then find the value of k.
2 has to increase its speed by 25 km/hr from its usual
18. Solve for x : √ 3x2− 2 √ 2 x − 2√ 3 = 0
19. If α and β are the zeroes of the quadratic polynomial
1 1
f(x) = x2 - 2x – 8, then find the value of
α
+ β
. taken 30 minutes less for the journey. Find the original
20. If α and β are the zeroes of the quadratic polynomial
1 1
f(x) = 6x2 + x – 2, then find the value of -
α β
-------------------------------------------------------
QUADRATIC EQUATION
4-MARKS & 3-MARKS
DIRECT PROBLEMS:
1) A natural number, when increased by 12, equals 160
times its reciprocal. Find the number.
2) Had Ajita scored 10 more marks in her mathematics
test out of 30 marks, 9 times these marks would have
been the square of her actual marks. How many marks
did she get in the test?
3) The base of a triangle is 4 cm longer than its altitude. If
the area of the triangle is 48 sq. cm, then find its base
and altitude.
4) A pole has to be erected at a point on the boundary of a
circular park of diameter 13 metres in such a way that
the differences of its distances from two diametrically
opposite fixed gates A and B on the boundary is 7
metres. Is it possible to do so? If yes, at what distances
from the two gates should the pole be erected?
5) The diagonal of a rectangular field is 60 metres more
than the shorter side. If the longer side is 30 metres
more than the shorter side, find the sides of the field.
6) A cottage industry produces a certain number of
pottery articles in a day. It was observed on a
particular day that the cost of production of each
article (in rupees) was 3 more than twice the number
of articles produced on that day. If the total cost of
production on that day was ` 90, find the number of
articles produced and the cost of each article.
7) Find two consecutive odd positive integers, sum of
whose squares is 290.
8) Find a natural number whose square diminished by 84
is equal to thrice of 8 more than the given number.
TRAIN AND SPEED:
1) A train, travelling at a uniform speed for 360 km, would
have taken 48 minutes less to travel the same distance
of the train.
2) A train travels at a certain average speed for a distance
of 63 km and then travels a distance of 72 km at an
average speed of 6 km/h more than its original speed.
If it takes 3 hours to complete the total journey, what is
its original average speed?
3) A car left 30 minutes later than the scheduled time. In
order to reach its destination 150 km away in time, it
speed. Find its usual speed.
4) A train covers a distance of 90 km at a uniform speed.
Had the speed been 15 km/hr more, it would have
speed of the train.
5) Two trains leave a railway station at the same time.
The first train travels due west and the second train
due north. The first train travels 5 km/hr faster than
the second train. If after two hours, they are 50 km
apart, find the average speed of each train.
6) Passenger train takes 1 hr more than an express train
to travel a distance of 240 km from Chennai to
Virudhachalam. The speed of passenger train is less
than that of an express train by 20 km per hour. Find
the average speed of both the trains.
7) A train travels a distance of 480 km at a uniform speed.
If the speed had been 8 km/h less, then it would have
taken 3 hours more to cover the same distance. We
need to find the speed of the train.
8) An express train takes 1 hour less than a passenger
train to travel 132 km between Mysore and Bangalore
(without taking into consideration the time they stop at
intermediate stations). If the average speed of the
express train is 11km/h more than that of the
passenger train, find the average speed of the two
trains
9) A train travels 360 km at a uniform speed. If the speed
had been 5 km/h more, it would have taken 1 hour
less for the same journey. Find the speed of the train.
AGE RELATED PROBLEMS:
1) If Zeba were younger by 5 years than what she really
is, then the square of the age (in years) would have
been 11 more than five times her actual age. What is
 her age now? At present Asha’s age (in years) is 2 more
than the square of her daughter
2) Nisha’s age. When Nisha grows to her mother’s
present age, Asha’s age would be one year less than 10
times the present age of Nisha. Find the present ages
of both Asha and Nisha.
3) One year ago, a man was 8 times as old as his son.
Now his age is equal to the square of his son’s age.
Find their present ages.
4) Rohan’s mother is 26 years older than him. The
product of their ages (in years) 3 years from now will
be 360. We would like to find Rohan’s present age.
BOAT AND STREAM
1) The speed of a boat in still water is 15 km/hr. It goes
30 km upstream and return downstream to the
original point in 4 hrs 30 minutes. Find the speed of
the stream.
2) A motor boat whose speed is 18 km/h in still water
takes 1 hour more to go 24 km upstream than to
return downstream to the same spot. Find the speed
of the stream.
3) The time taken by a person to cover 150 km was
1 (k – 12)x2 + 2(k – 12)x + 2 = 0 has 2 real equal roots.
2 hours more than the time taken in the return
2 7) Find the value of k for which the quadratic equation
journey. If he returned at a speed of 10 km/hour more
thanthe speed while going, find the speed per hour in
each direction.
COMPLETING THE SQUARES
1) Check whether the equation 6x2 – 7x + 2 = 0 has real
roots, and if it has, find them by the method of
completing the squares.
2) Solve the quadratic equation 5x2- 6x -2 = 0 by M.C.S
3) Solve the equation a2 x2- 3abx+ 2b2 = 0 by M.C.S
4) Find the roots of the equation 5x2 – 6x – 2 = 0 by the
method of completing
5) Find the roots of 4x2 + 3x + 5 = 0 by the method of
completing the square.
6) Find the roots of 2x2 – 5x + 3 = 0 by the method of
completing the square.
7) Find the roots of 5x2 – 6x – 2 = 0 by the M.C.S
8) Find the roots of 4x2 + 3x + 5 = 0 by M.C.S
9) Find the roots of 2x2 + x + 4 = 0 by M.C.S
TIME AND WORK
1) A takes 6 days less than the time taken by B to finish a
piece of work. If both A and B together can finish it in
4 days, find the time that B would take to finish this
work by himself.
2) Two water taps together can fill a tank in 75/8 hours.
The tap of larger diameter takes 10 hours less than the
smaller one to fill the tank separately. Find the time in
which each tap can separately fill the tank.
1
3) Two pipes running together can fill a tank in 11 min.
9
If one pipe takes 5 minutes more than the other to fill
the tank, find the time in which each pipe would fill
the tank separately.
4) The denominator of a fraction is two more than its
numerator. If the sum of the fraction and its reciprocal
is 34/15 , find the fraction.
NATURE OF ROOTS
1) Find the value of k for which the quadratic equation
2x2 + kx + 3 = 0 has two real equal roots.
2) Find the value of k for which the quadratic equation
kx(x – 3) + 9 = 0 has two real equal roots.
3) Find the value of k for which the quadratic equation
4x2 – 3kx + 1 = 0 has two real equal roots..
4) If –4 is a root of the equation x 2 + px – 4 = 0 and the
equation x2 + px +q = 0 has equal roots, find the
value of p and q.
5) If –5 is a root of the equation 2x2 + px – 15 = 0 and the
equation p(x2 + x) +k = 0 has equal roots, find the
value of k.
6) Find the value of k for which the quadratic equation
k2x2 – 2(k – 1)x + 4 = 0 has two real equal roots..
8) If roots of the equation (a – b)x 2 + (b – c)x + (c – a) =
0 are equal, prove that b + c = 2a.
9) Prove that both the roots of the equation
(x – a)(x – b) + (x – b)(x – c)+ (x – c)(x – a) = 0 are
real but they are equal only when a = b = c.
10) Find the positive value of k for which the equation
x2 + kx +64 = 0 and x2 – 8x +k = 0 will have real roots.
11) Find the value of k for which the quadratic equation
kx2 – 6x – 2 = 0 has two real roots.
12) Find the value of k for which the quadratic equation
3x2 + 2x + k= 0 has two real roots.
13) Find the value of k for which the quadratic equation
2x2 + kx + 2 = 0 has two real roots.
14) Show that the equation 3x2 + 7x + 8 = 0 is not true for
any real value of x.
15) Show that the equation 2(a2 + b2)x2 + 2(a + b)x + 1 =
0 has no real roots, when a ≠ b.
16) Find the value of k for which the quadratic equation
kx2 + 2x + 1 = 0 has two real and distinct roots.
17) Find the value of p for which the quadratic equation
2x2 + px + 8 = 0 has two real and distinct roots.
18) If the equation (1 + m2)x2 + 2mcx + (c2 – a2) = 0 has
equal roots, prove that c2 = a2(1 + m2).
19) If the roots of the equation (c 2 – ab)x2 – 2(a2 – bc)x +
(b2 – ac) = 0 are real and equal, show that either a = 0
or (a3 + b3 + c3) = 3abc.
20) Find the value of k for which the quadratic equation
9x2 + 8kx + 16 = 0 has two real equal roots.
21) Find the value of k for which the quadratic equation
(k + 4)x2 + (k+1)x + 1 = 0 has two real equal roots.
22) Prove that x2(a2 + b2) + 2x(ac + bd) + (c 2 + d2) = 0
has no real root, if ad ≠bc.
23) If the roots of the equation x 2 + 2cx + ab = 0 are real
unequal, prove that the equation
x2 – 2(a+ b) + a2 + b2 + 2c2 = 0 has no real roots.
24) Find the positive values of k for which the equation
x2 + kx + 64 = 0 and x 2 – 8x + k = 0 will both have
real roots.
25) Find the value of k for which the quadratic equation
(k + 4)x2 + (k + 1)x + 1 = 0 has equal roots.
26) Find the value of k for which the quadratic equation
k2x2 – 2(2k – 1)x + 4 = 0 has real and equal roots.
27) Find the value of k for which the quadratic equation
(k + 1)x2 – 2(k – 1)x + 1 = 0 has real and equal roots.
28) Find the value of k for which the quadratic equation
(4 – k)x2 + (2k + 4)x + (8k + 1) = 0 has real and
equal roots.
29) Find the value of k for which the quadratic equation
(2k + 1)x2 + 2(k + 3)x + (k + 5) = 0 has real and
equal roots.
( )
2
2X 2X
30) Solve for x : + = 24, x≠0
X −5 X−5
a b 2c
31) Find x in terms of a, b and c : + = x≠
x−a x−b x−c
a, b, c
32) Find the value of k for which the quadratic equation
x2 – 2(k + 1)x + k2 = 0 has real and equal roots.
TWO-DIGIT PROBLEMS
33) A two digit number is such that the product of its
digits is 12. When 36 is added to the number, the
digits are reversed. Find the number.
34) A two digit number is such that the product of its
digits is 8. When 54 is subtracted from the number,
the digits are reversed. Find the number.
35) A two digit number is four times the sum and twice
the product of its digits. Find the number
36) A two digit number is such that the product of its
digits is 14. When 45 is added to the number, the
digits interchange their places. Find the number.
37) A two digit number is such that the product of its
digits is 18. When 63 is subtracted from the number,
the digits interchange their places. Find the number.
38) A two digit number is four times the sum and three
times the product of its digits. Find the number
39) A two digit number is such that the product of its
digits is 8. When 18 is subtracted from the number,
the digits are reversed. Find the number.
----------------------------------------------------------
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
SOLVING EQUATIONS
4-MARKS & 3-MARKS
1) Solve: 11x + 15y + 23 = 0; 7x – 2y –20 =0.
2) Solve: 2ax +3by =a + 2b; 3ax + 2by = 2a + b.
3) Find the value of k, so that the system of equations has
no solution: 3x – y – 5 = 0; 6x – 2y – k = 0.
4) Find the value of k, so that the system of equations has
a non-zero solution: 3x + 5y = 0; kx + 10y = 0.
5) Find the value of k, so that the system of equations has
a unique solution :x +2y = 3; 3x +ky =1
6) For what value of k, the following pair of linear
equations has infinite number of solutions:
kx + 3y =(2k +1); 2(k+1)x + 9y = (7k +1)
7) Find the value of k, so that the system of equations has
a non-zero solution: 5x – 3y = 0; 2x + ky = 0.
8) Show that the system of the equations has a unique
solution and hence find the solution of the given
equations. 3x + 5y =12; 5x + 3y = 4.
9) For Uttarakhand flood victims two sections A and B of
class contributed Rs. 1,500. If the contribution of X-A
was Rs. 100 less than that of X-B, find graphically the
amounts contributed by both the sections.
10) Solve system of linear equations graphically:
x + 2y = 3; 4x +3y = 2.
11) Solve the following pair of equations :
2 3 4 9
+ =2 & - = -1
√x √ y √x √ y
12) Solve for x and y : 2x − y + 3 = 0 & 3x − 5y + 1 = 0
TWO-DIGIT PROBLEMS
1) The sum of the digits of a two digit number is 9. Also,
nine times this number is twice the number obtained by
reversing the order of the digits. Find the number.
2) The sum of the digits of a two digit number is 9. If 27 is
added to it, the digits of the numbers get reversed. Find
the number.
3) The sum of a two-digit number and the number
obtained by reversing the digits is 66. If the digits of the
number differ by 2, find the number. How many such
numbers are there?
4) A two-digit number is 4 more than 6 times the sum of its
digit. If 18 is subtracted from the number, the digits are
reversed. Find the number.
5) A two digit number is obtained by either multiplying the
sum of digits by 8 and then subtracting 5 or by
multiplying the difference of digits by 16 and adding 3.
Find the number.
6) The sum of a two-digit number and the number
obtained by reversing the digits is 99. If the digits differ
by 3, find the number.
7) The sum of a two-digit number and the number formed
by interchanging its digit is 110. If 10 is subtracted from
the original number, the new number is 4 more than 5
times the sum of the digits of the original number. Find
the original number.
8) 4 chairs and 3 tables cost Rs 2100 and 5 chairs and 2
tables cost Rs 1750. Find the cost of none chair and
one table separately.
9) If a bag containing red and white balls, half thenumber
of white balls is equal to one-third the number of red
balls.Thrice the total number of balls exceeds seven
times the number of white balls by 6. How many ballsof
each colour does the bag contain ?
SPEED, DISTANCE AND TIME RELATED QUESTIONS
10) A and B are two points 150 km apart on a highway.
Two cars start A and B at the same time. If they move in
the same direction they meet in 15 hours. But if they
move in the opposite direction, they meet in1 hours.
Find their speeds.
11) A train covered a certain distance at a uniform speed. If
the train would have been 10 km/hr scheduled time.
And, if the train were slower by 10 km/hr, it would
have taken 3 hr more than the scheduled time. Find the
distance covered by the train.
12) A boat goes 30 km upstream and 44 km downstream in
10 hours. In 13 hours, it can go 40 km upstream and 55
km down-stream. Determine the speed of the stream
and that of the boat in still water.
13) Places A and B are 100 km apart on a highway. One car
starts from A and another from B at the same time. If
the cars travel in the same direction at different speeds,
they meet in 5 hours. If they travel towards each other,
they meet in 1 hour. What are the speeds of the 2 cars?
14) A train covered a certain distance at a uniform speed. If
the train would have been 10 km/h
15) faster, it would have taken 2 hours less than the
scheduled time. And, if the train were slower by
10 km/h; it would have taken 3 hours more than the
scheduled time. Find the distance covered by the train.
16) Ritu can row downstream 20 km in 2 hours, and
upstream 4 km in 2 hours. Find her speed of rowing in
still water and the speed of the current.
17) Roohi travels 300 km to her home partly by train and
partly by bus. She takes 4 hours if she travels 60 km by
train and the remaining by bus. If she travels 100 km
by train and the remaining by bus, she takes 10
minutes longer. Find the speed of the train and the bus
separately.
18) A boat covers 32 km upstream and 36 km downstream
in 7 hours. In 9 hours, it can cover 40 km upstream and
48 km down-stream. Find the speed of the stream and
that of the boat in still water.
19) Two places A and B are 120 km apart on a highway. A
car starts from A and another from B at the same time.
If the cars move in the same direction at different
speeds, they meet in 6 hours. If they travel towards
each other, they meet in 1 hours 12 minutes. Find the
speeds of the two cars.
TIME AND WORK RELATED QUESTIONS
20) 2men and 7 boys can do a piece of work in 4 days. The
same work is done in 3 days by 4 men and 4 boys. How
long would it take one man and one boy to do it alone.
21) 2 women and 5 men can together finish an embroidery
work in 4 days, while 3 women and 6 men can finish it
in 3 days. Find the time taken by 1 woman alone to
finish the work, and also that taken by 1 man alone.
22) 8 men and 12 boys can finish a piece of work in 10 days
while 6 men and 8 boys finish it in 14 days. Find the
time taken by one man alone and by one boy alone to
finish the work.
23) 8 men and 12 boys can finish a piece of work in 5 days
while 6 men and 8 boys finish it in 7 days. Find the time
taken by 1 man alone and by 1 boy alone to finish the
work.
24) 2 men and 5 boys can do a piece of work in 4 days. The
same work is done by 3 men and 6 boys in 3 days. .
Find the time taken by 1 man alone and by 1 boy alone
to finish the work.
25) The ratio of incomes of two persons is 9 : 7 and the
ratio of their expenditures is 4 : 3. If each of them
manages to save Rs 2000 per month, find their monthly
incomes.
26) The taxi charges in a city consist of a fixed charge
together with the charge for the distance covered. For a
distance of 10 km, the charge paid is Rs 105 and for a
journey of 15 km, the charge paid is Rs 155. What are
the fixed charges&the charge per km? How much does
a person have to pay for travelling a distance of 25 km?
GEOMETRICAL FIGURES RELATED QUESTIONS
27) The area of a rectangle gets reduced by 9 square units,
if its length is reduced by 5 units and breadth is
increased by 3 units. If we increase the length by 3
units and the breadth by 2 units, the area increases by
67 square units. Find the dimensions of the rectangle.
28) The length of a room exceeds its breadth by 3 metres. If
the length is increased by 3 metres and the breadth is
decreased by 2 metres, the area remains the same. Find
the length and the breadth of the room.
29) The area of a rectangle gets reduced by 8m2, if its
length is reduced by 5m and breadth is increased by
3m. If we increase the length by 3m and the breadth by
2m, the area increases by74m2. Find the length and the
breadth of the rectangle.
----------------------------------------------------------------------
ARITHMETIC PROGRESSIONS
(4-MARKS & 3-MARKS)
1) If the mth term of an AP be 1/n and its nth term be 1/m
then show that its (mn)th terms is 1.
2) If m times the mth term of an AP is equal to n times the
nth term and m≠ n, show that its (m + n)th term is 0.
3) If the pth term of an AP is q and qth term of an AP is p,
prove that its nth is (p + q – n).
4) If the pth, qth and rth terms of an AP is a, b, c
respectively, then show that
a(q – r) + b(r – p)+ c(p – q) = 0.
5) The sum of three numbers in AP is 15 and their product
is 80. Find the numbers.
6) The sum of three consecutive terms of an AP is 21 and
the sum of the squares of these terms is 165. Find the
terms.
7) Which term of the AP 9, 12, 15, 18,…. will be 39 more
than its 36th term?
8) Find the sum of first 25 terms of an AP whose nth term
is given by (7 – 3n).
9) If the sum of the first m terms of an AP be n and the
sum of first n terms be m then show that the
sum of its first (m + n) terms is –(m + n).
10) If the sum of the first p terms of an AP is the same as
the sum of first q terms (where p +q) then show that
the sum of its first (p + q) terms is 0.
11) If the sum of first n, 2n and 3n terms of an AP be S1, S2
and S3 respectively, then prove that S3 =3(S2 – S1).
12) Find the sum of first 51 terms of an AP whose second
and third terms are 14 and 18 respectively.
13) The sum of first 8 terms of an AP is 100 and the sum of
its first 19 terms is 551. Find the AP.
14) How many two-digit numbers are divisible by 3?
15) For what value of n, are the nth terms of two APs: 63,
65, 67, . . . and 3, 10, 17, . . . equal?
16) Two APs have the same common difference. The
difference between their 100th terms is100, what is the
difference between their 1000th terms?
17) How many terms of the AP : 24, 21, 18, . . . must be
taken so that their sum is 78?
18) The sum of the third and the seventh terms of an AP is
6 and their product is 8. Find the sum of first sixteen
terms of the AP.
2
3 n 13 n
19) In an A.P. the sum of first n terms is + . Find
2 2
the 25th term.
20) Divide 56 in four parts in A.P. such that the ratio of the
product of their extremes (1st and 4rd ) to the product
of means (2nd and 3rd ) is 5:6.
1
21) If the sum of the first n terms of an A.P. is (3n2 +7n).
2
then find its nth term. Hence write its 20th term.
22) For what value of n, are the nth terms of two A.Ps 63,
65, 67, ... and 3, 10, 17, .... equal?
23) In an A.P., if the 12th term is −13 and the sum of its
first four terms is 24, find the sum of its first ten terms.
24) The tenth term of an A.P., is −37 and the sum of its first
six terms is −27. Find the sum of its first eight terms.
25) If 7th term of an A.P. is 1/9 and 9th term is , 1/7 find
63rd term.
26) Determine an A.P. whose third term is 9 and when fifth
term is subtracted from 8th term, we get 6.
27) The ninth term of an A.P. is equal to seven times the
second term and twelfth term exceeds five times the
third term by 2. Find the first term and the common
difference.
28) In an A.P., first term is 5, common difference is 3 and
nth term is 50. Find the value of n and sum of its first n
terms.
29) Find the sum of integers between 100 and 200 that are
divisible by 9.
30) Find the 20th term of an A.P. whose 3rd term is 7 and
the seventh term exceeds three times the 3rd term by
2. Also find its nth term an .
31) A spiral is made up of successive semicircles, with
centres alternately at A and B, starting with centre at A,
of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in
Fig.. What is the total length of such a spiral made up of
thirteen consecutive semicircles?
 No. of 0- 6- 10- 14- 20- 28- 38-
days 6 10 14 20 28 38 40
--------------------------------------------------------------------- No. of 1 10 7 4 4 3 1
students 1

STATISTICS
(4-MARKS & 3-MARKS)
9) If the mean distribution is 25, Then find p.
1) Find the mode of the following
Class 0-10 10-20 20-30 30-40 40-50
Xi 35 38 4 42 44
Frequency 5 18 15 P 6
0
fi 5 9 1 7 2
10) Find the value of p if the median of the following
2) Write the median0class of the following distribution.
frequency distribution is 50
CI 0-10 10-20 20- 30- 40- 50- 60-
Class 20- 30- 40- 50- 60- 70- 80-
30 40 50 60 70
30 40 50 60 70 80 90
f 4 4 8 10 12 8 4
Frequency 25 15 P 6 24 12 8

3) Write the sum of lower limits of the median class and

11) The frequency distribution table of donation of a class
modal class of the following distribution:
X students from their pocket money to PM relief fund is
Class 0-5 5-10 10-15 15-20 20-25
given below. find the mean of the following frequency
Frequency 10 15 12 20 9
distribution using step deviation method. Which
quality of class X is being depicted in the question?
4) Calculate the mean of the following distribution Money Rs 0-10 10-20 20-30 30-40 40-50
Class 50- 60- 70- 80- 90- Frequency 7 12 13 10 8
interval 60 70 80 90 100
Frequency 8 6 12 11 13 12) Find the median of the following data
C Less Less Less Less Less Less Less Less
5) Find the mode of the following frequency distribution I Than Than Than Than Than Than Than than
10 30 50 70 90 110 130 150
C.I 10-20 20-30 30-40 40-50 50-60
F 0 10 25 43 65 87 96 100
f 12 35 45 25 13

13) During the medical checkup of 35 students of

6) Find the median of the following distribution class ,their weights were recorded as follows: Draw a
C.I 0- 10-20 20-30 30-40 40-50 50-60 less than type and more than type Ogive from given
10 data. Hence obtain the median from the graph.
F 5 8 20 15 7 5 Weight in 38- 40- 42- 44- 46- 48- 50-
kg 40 42 44 46 48 50 52
7) A class teacher has the following absentee record of 40 No. of 3 2 4 5 14 4 3
students of a class for the whole term. students
No. of 0- 6- 10- 14- 20- 28- 38-
days 6 10 14 20 28 38 40 14) The mean of the following frequency distribution is 50
No. of 11 10 7 4 4 3 1 and the sum of the observations is 120. Find the
students missing frequencies f1 and f2.
C.I 0-20 20-40 40-60 60-80 80-100
8) Write the distribution as less than type and more than F 17 f1 32 f2 19
type cumulative frequency distribution.
15) The following distribution give the daily income of 65 21) If the median of the following data is 32.5. Find the
workers of a factory. Convert the above to a more value of x and y.
than type cumulative frequency distribution and draw C. 0- 10 20 30 40 50 60 Tota
its ogive. l 1 - - - - - - l
Daily 100- 120- 140- 160- 180- 0 20 30 40 50 60 70
income 120 140 160 180 200 f x 5 9 12 Y 3 2 40
No. of 14 16 10 16 9
workers 22) The mean of the following distribution is 18. the
frequency f is missing .Determine f.
C 11- 13- 15- 17- 19- 21- 23-
I 13 15 17 19 21 23 25
f 3 6 9 13 f 5 4
CI 0-6 6-12 12-18 18-24 24-30 Total
f 4 x 5 y 1 20
23) The following distribution gives the weights of 60
students of a class. Find the mean and mode weights
15) If the median of the following data is 14.4Find the value
of the students.
of x and y.
Weight students
16) Find the value of p, if the mean of the following
40-44 4
distribution is 18.
44-48 6
Variants (xi) 13 15 17 19 20+p 23
48-52 10
Frequency (fi) 8 2 3 4 5p 6
52-56 14
17) Find the mean, mode and median for the data.
56-60 10
Cl 0- 10- 20- 30- 40- 50- 60-
60-64 8
10 20 30 40 50 60 70
64-68 6
f 5 8 15 20 14 8 5
68-72 2
18) The median of the following data is 52.5. find the value 24) On the sports day of a school, 300 student
of x and y, if the total frequency is 100. participated. Their ages are given in the following
C.I 0- 10- 20- 30- 40- 50- 60- 70- 80- 90-
distribution
10 20 30 40 50 60 70 80 90 100
f 2 5 X 12 17 20 Y 9 7 4 CI 5-7 7-9 9-11 11-13 13-15 15-17 17-19
f 67 33 41 95 36 13 15
19) Draw ‘less than ogive’ and ‘more than ogive’ for the 25) Monthly expenditures on milk in 100 families of
following distribution and hence find its median. ahousing society are given in the following frequency
distribution : Monthly. Find the mode and median for
Cl 20- 30- 40- 50- 60- 70- 80-
the distribution.
30 40 50 60 70 80 90
expenditure No. of families
f 10 8 12 24 6 25 15
0 -175 10
175-350 14
20) The following table shows age distribution of persons
350-525 15
in a particular region. Calculate the median age
525-700 21
Age in years No. of persons
700-875 28
Below 10 200
Below 20 500 875-1050 7
Below 30 900 1050-1125 5
Below 40 1200 26) Find the median of the following data :
Below 50 1400 Class Interval Frequency
Below 60 1500 0-20 6
Below 70 1550 20-40 8
Below 80 1560 40-60 10
60-80 12
80-100 6
 100-120 5 and AC.
120-140 3 13) Find the ratio in which the point p(m, 6) divides the
How can we find the median graphically ?
27) Find the value of x and y , if the median for the
following data is 31.
Cl 0-10 10-20 20-30 30-40 40-50 50-60
f 5 x 6 y 6 5
-------------------------------------------------------------------
COORDINATE GEOMETRY
(4-MARKS & 3-MARKS)
DISTANCE FORMULA
1) The base BC of an equilateral triangle ABC lies on y-
axis. The co-ordinates of point C are (0,3). The origin is
the mid-point of the base. Find the coordinates of the
point A and B. Also find the coordinates of another
point D such that BACD is a rhombus.
2) Prove that the area of a triangle with vertices (t, t − 2),
(t + 2, t + 2) and (t + 3) is independent of t.
3) If P(−5,− 3),Q(−4, − 6) ,R(2, − 3) and S(1, 2) are the
vertices of a quadrilateral PQRS, find its area.
4) P(9a − 2,− b) divides the line segment joining
A(3a + 1, − 3) and B(8x, 5) in the ratio 3:1. Find the
values of a and b.
5) Find the values of k so that the area of the ∆le with
vertices (k + 1,1), (4, − 3)& (7, − k) is 6 sq units.
6) The base QR of an equilateral triangle PQR lies on x-
axis. The co-ordinates of point Q are (−4,0) and the
origin is the mid-point of the base. find the coordinates
of the point P and R.
7) Find the coordinates of the point which divide the line
segment joining A(2,− 3) and B(−4,− 6) into three
equal parts.
8) Find the values of k for which the points A(k + 1, 2k) ,
B(3k,2k + 3) and C(5k − 1, 5k) are collinear.
9) Prove that the point (3,0), (6,4) and (−1, 3) are the
vertices of a right angled isosceles triangle
10) If A(5,2), B(2, − 2) and C(−2, t) are the vertices of a
right angled triangle with angle B = 90o, then find the
value of t.
11) For what values of k are the points (8,1), (3, − 2k)
and (k, − 5) collinear?
12) The vertices of ∆ABC are A(6, − 2) ,B(0, − 6) and
C(4,8). Find the co-ordinates of mid-points of AB,BC
line segment joining the points A(−4, 3) and B(2, 8).
Also find the value of m.
14) Find the coordinates of the point which divides the line
segment joining the points A(4, –3) and B(9, 7) in the
ration 3 : 2.
15) The coordinates of the midpoint of the line segment
joining the points A(2p + 1, 4) and B(5, q–1)are(2p, q).
Find the value of p and q.
16) Find the coordinates of the points of trisection of the
line segment joining the points (4, –1) and(–2, –3).
17) Find the area of a triangle formed by the points A(1, –
1), B(– 4, 6) and C(– 3, – 5).
18) Find the value of k if the points A(7, –2), B(5, 1) and
C(3, k) are collinear.
19) Find the area of the triangle formed by joining the
midpoints of the sides of the triangle whose vertices
are (0, –1), (2, 1) and (0, 3). Find the ratio of this area
to the area of the given triangle.
20) If (x, y) be on the line joining the two points (1, –3) and
(–4, 2), prove that x + y + 2 = 0.
21) Find the condition that the point (x, y) may lie on the
line joining (3, 4) and (–5, –6).
22) Find the value of k for which the area formed by the
triangle with vertices A(4, 4), (3, k) and C(3, –2) is 7
square units.
23) The x-coordinate of a point P is twice its y-coordinate.
If P is equidistant from Q(2,− 5) and R(−3,6), find
the co-ordinates of P.
24) Find the altitude of an equilateral triangle when each
of its side is 'a' cm.
25) If the co-ordinates of points A and B are (−2,− 2)
and (2, − 4) respectively, find the co-ordinates of
P such that AP =3/7AB, where P lies on the line
segment AB.
26) Find the ratio in which the line segment joining the
points A(3, − 3) and B(−2, 7) is divided by x-axis.
Also find the co-ordinates of point of division.
27) Find the point on the x-axis which is equidistant from
the points (2, - 5) and (-2,9).
28) Show that A(6, 4), B(5, - 2) and C(7,- 2) are the vertices
of an isosceles triangle.
29) Prove that the diagonals of a rectangle ABCD, with
vertices A(2, - 1), B(5, - 1), C(5,6) and D(2,6) are
equal and bisect each other.
30) The vertices of quadrilateral ABCD are A(5, - 1),
B(8, 3), C(4, 0) and D(1, - 4). Prove that ABCD is
a rhombus.
31) The co-ordinates of the vertices of TABC are A(7,2),
B(9,10) and C(1,4). If E and F are the mid-points
of AB and AC respectively, prove that EF =1/2 BC 2.
32) If R(x, y) is a point on the line segment joining
the points P(a, b) and Q(b, a), then prove that
x + y = a + b.
33) Find the ratio in which the line segment joining the
points A(3, - 3) and B(-2, 7) is divided by x-axis.
Also find the co-ordinates of point of division.
-----------------------------------------------------------------------
PROBABLITY
(4-MARKS & 3-MARKS)
1) The record of a weather station shows that out of the
past 250 consecutive days, its weather forecasts were
correct 175 times.
(i) What is the probability that on a given day it was
correct?
(ii) What is the probability that it was not correct on a
given day?
2) Cards are marked with numbers 4, 5, 6, …….50 are
placed in the box and mixed thoroughly. One card is
drawn at random from the box. What is the probability
of getting
a) a two-digit number b) a perfect square number
c) a number divisible by 5.
d) a number divisible by 2 or 3.
3) There are 30 cards numbered from1 to 30. One card is
drawn at random. Find the probability of getting the
card with
a) a two-digit number b) a perfect square number
c) a number divisible by 5.
d) a number divisible by 2 or 3.
4) Tickets numbered 2, 3, 4, 5, …..100, 101 are placed in a
box and mixed thoroughly. One ticket is drawn at
random from the box. Find the probability that the
number on the ticket is
a) a two-digit number
b) a perfect square number
c) a number divisible by 5.
d) a number divisible by 2 or 3.
5) A box contains 12 balls out of which x are black. If one
ball is drawn at random from the box, what is the
probability that it will be a black ball? If 6 more black
balls are put in the box, the probability of drawing a
black ball is now double of what it was before. Find x.
6) A bag contains 5 red balls and some blue balls. If the
probability of drawing a blue ball is double that of a red
ball, determine the number of blue balls in the bag.
7) Two customers are visiting a particular shop in the
same week (Monday to Saturday). Each is equally likely
to visit the shop on any day as on another day. What is
the probability that both will visit the shop on
(i) the same day?
(ii) consecutive days?
(iii) different days?
8) A bag contains 3 red balls and 5 black balls. A ball is
drawn at random from the bag. What is the probability
that the ball drawn is red and not red?
9) A bag contains 9 blue, 4 black, 5 red and 7 white balls.
One ball is taken out of the bag and found red ball then
again one ball is taken out at random from the
remaining. What is the Probability that it will be
a) black? b) white or blue? c) not blue ball?
d) neither blue ball nor red ball?
10) Three coins are tossed simultaneously. What is the
probability of getting
i) exactly two heads
ii) at least two heads
iii) at most two heads
iv)one head or two heads
11) All spades are removed from a well shuffled deck of 52
cards and then one card is drawn randomly from the
remaining cards. Find the probability of getting
(a) neither a heart nor a king
(b) neither an ace nor a king
(c) neither a red card nor a queen card
(d) a black card or an ace.
12) One card is drawn from a well-shuffled deck of 52
cards. Find the probability of getting
(a) an ace card (b) a red card
(c) either red or king card (d) red and a king
13) Two dice are thrown simultaneously. What is the
probability that the sum of the numbers appearing on
the dice is
(i) 7? (ii) a prime number? (iii) 1?
14) Two dice are thrown simultaneously. Find the
probability of getting
(i) the sum equal to 12.
(ii) the sum greater than equal to 10
(iii) the sum less than or equal to 10
(iv) the sum as a prime number
15) Three coins are tossed simultaneously. What is the
probability of getting
i) exactly two heads ii)at least two heads
 iii). at most two heads iv) one head or two heads
-----------------------------------------------------------------------
CIRCLES
(4-MARKS & 3-MARKS)
1) In the given figure, O is the centre of the circle. Find
∠ APC , if DA and DC are tangents and ∠ADC =500.
2) Prove that opposite sides of a quadrilateral
circumscribing a circle subtend supplementary angles
at the centre of the circle.
3) In figure, PQ, is a chord of length 16 cm, of a circle of
radius 10 cm. the tangents at P and Q intersect at a
point T . Find the length of TP.
4) In the figure, PQ is a tangent to a circle with center O. If
∠OAB = 300, find ∠ABP and ∠AOB.
5) Two tangents TP and TQ are drawn to a circle with
centre O from an external point T . Pt ∠PTO =∠ OPQ
6) Prove that “The tangent at any point of a circle is
perpendicular to the radius through the point of
contact”.
7) Prove that “The lengths of tangents drawn from an
external point to a circle are equal.”
8) Prove that the parallelogram circumscribing a circle is
a rhombus.
9) In the given figure, PA& PB are tangents to a circle from
an external point P such that PA=4cm & ∠BAC = 1350
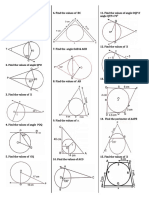
Find the length of chord AB.
10) Prove that “The centre lies on the bisector of the angle
between the two tangents drawn from an external
point to a circle.”
11) In the given figure, OP is equal to the diameter of a
circle with center O and PA and PB are tangents. Prove
that ABP is an equilateral triangle.
12) Find the length of the tangent drawn to a circle of
radius 3 cm, from a point distant 5 cm from the centre.
13) Prove that the perpendicular at the point of contact to
the tangent to a circle passes through the centre.
14) Prove that the angle between the two tangents drawn
from an external point to a circle is supplementary to
the angle subtended by the line-segment joining the
points of contact at the centre.
15) Prove that opposite sides of a quadrilateral
circumscribing a circle subtend supplementary angles
at the centre of the circle.
16) Two tangents PA and PB are drawn to the circle with
center O, such that ∠APB = 1200. Prove that OP = 2AP.
17) A circle is touching the side BC of ΔABC at P and is
touching AB and AC when produced at Q and R
respectively. Prove that AQ = ½ (Perimeter of Δ ABC).
18) A quadrilateral ABCD is drawn to circumscribe a circle
Prove that AB + CD = AD + BC
19) In Fig., XY and X′Y′ are two parallel tangents to a circle
with centre O and another tangent AB with point of
contact C intersecting XY at A and X′Y′ at B. Prove that
∠ AOB = 90°.
 TRIANGLES
(4-MARKS & 3-MARKS)
1) Prove that in a right angled triangle the square of
hypotenuse is equal to the sum of the squares of the
other two sides.
2) If a line is drawn parallel to one side of a triangle to
intersect the other two sides in distinct points, prove
that the other two sides are divided into the same ratio.
3) ∆ ABC is right angled at B and D is midpoint of side BC.
Prove that AC² = 4AD² - 3 AB²
4) Prove that the ratio of the areas of two similar triangles
is equal to the ratio of square of their
corresponding sides.
5) In a ∆ , if the square of one side is equal to sum of the
squares of the other two sides, prove that the angle
opposite to the first side is a right angle.
6) In an equilateral ∆ ABC, D is a point on the side BC, such
that BD = 1/3BC. Prove that 9 AD² = 7 AB²
7) P and Q are the mid points of side CA and CB
respectively of ∆ ABC right angled at C. Prove that
4(AQ²+ BP²) = 5 AB² .
8) ABCD is a trapezium in which AB || DC & its diagonals
intersect each other at the point O. Show that
OA.DO=BO.CO
9) CM and RN are respectively the medians of ∆ABC and
∆PQR. If ∆ABC~∆PQR, prove that(i) ∆AMC~∆PNR
(ii) CM/RN=AB/P (iii) ∆CMB~∆RNQ
10) A girl of height 90 cm is walking away from the base of
a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m
above the ground, find the length of her shadow after
4 seconds.