Name: ________________________

AQA A Level Physics

Mechanics and Materials 3.4.1.3 Class: ________________________

Date: ________________________

Time: 77 minutes

Marks: 60 marks

Q1 to Q7 to be worked through with tutor. Q8 to Q15 to

Comments:
be worked through independently.

Arnold Hill Academy Page 1 of 25

 (a) (i) Define acceleration.
1
______________________________________________________________

(ii) State why acceleration is a vector quantity.

______________________________________________________________

______________________________________________________________
(2)

(b) State what feature of a velocity-time graph may be used to calculate

(i) acceleration,

______________________________________________________________

(ii) displacement.

______________________________________________________________
(2)

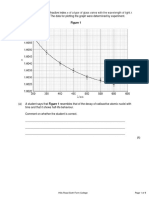
(c) The graph in Figure 1 shows how the displacement of a runner from a fixed point, along a
straight track, varies with time.

Figure 1

Arnold Hill Academy Page 2 of 25

 Without calculation, sketch on the grid in Figure 2 a graph to show how the velocity of the
same runner varies over the same period. The time scales are the same on both graphs.

Figure 2
(4)
(Total 8 marks)

A car accelerates uniformly from rest along a straight road. Which graph shows the variation of
2 displacement x of the car with time t?

A B C D

(Total 1 mark)

The graph shows how the vertical speed of a parachutist changes with time during the first 20 s
3 of his jump. To avoid air turbulence caused by the aircraft, he waits a short time after jumping
before pulling the cord to release his parachute.

Arnold Hill Academy Page 3 of 25

(a) Regions A, B and C of the graph show the speed before the parachute has opened. With
reference to the forces acting on the parachutist, explain why the graph has this shape in
the region marked

(i) A, ____________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

(ii) B, ____________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

(iii) C, ____________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________
(6)

Arnold Hill Academy Page 4 of 25

(b) Calculate the maximum deceleration of the parachutist in the region of the graph marked D,
which shows how the speed changes just after the parachute has opened. Show your
method clearly,

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(2)

(c) Use the graph to find the total vertical distance fallen by the parachutist in the first 10 s of
the jump. Show your method clearly.

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(4)

(d) During his descent, the parachutist drifts sideways in the wind and hits the ground with a
vertical speed of 5.0 m s–1 and a horizontal speed of 3.0 m s–1. Find

(i) the resultant speed with which he hits the ground,

______________________________________________________________

______________________________________________________________

______________________________________________________________

(ii) the angle his resultant velocity makes with the vertical.

______________________________________________________________

______________________________________________________________
(2)
(Total 14 marks)

Arnold Hill Academy Page 5 of 25

 A roller coaster car is raised to a height of 65 m and released from rest.
4
What is the maximum possible speed of the car?

A 11 m s−1

B 25 m s−1

C 36 m s−1

D 130 m s−1

(Total 1 mark)

A student measures the acceleration due to gravity, g, using the apparatus shown in the figure
5 below. A plastic card of known length is released from rest at a height of 0.50m above a light
gate. A computer calculates the velocity of the card at this point, using the time for the card to
pass through the light gate.

Arnold Hill Academy Page 6 of 25

(a) The computer calculated a value of 3.10 m s–1 for the velocity of the card as it travelled
through the light gate. Calculate a value for the acceleration due to gravity, g, from these
data.

answer = ______________________ m s–2

(2)

(b) The student doubles the mass of the card and finds a value for g that is similar to the
original value. Use the relationship between weight, mass and g to explain this result.

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(1)

(c) State and explain one reason why the card would give more reliable results than a table
tennis ball for this experiment.

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(2)
(Total 5 marks)

Arnold Hill Academy Page 7 of 25

 An object is dropped from a cliff. How far does the object fall in the third second?
6
Assume that g = 10 m s–2.

A 10 m

B 20 m

C 25 m

D 45 m

(Total 1 mark)

The first section of a full-size stroboscopic photograph of a marble released from rest and in free
7 fall is shown below. Every time the strobe light flashes an image of the marble is recorded. The
time interval between successive flashes of the strobe light was 0.0435 s.

(a) This photograph can be used to find a value for the acceleration due to gravity g.

(i) Take measurements from the diagram below that can be used to find an accurate
value for g.

(2)

(ii) Calculate a value for g using your measurements from (a)(i).

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________

______________________________________________________________
(2)

Arnold Hill Academy Page 8 of 25

(b) Suggest why the duration of the flash of the strobe should be as short as possible.

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(1)

(Total 5 marks)

Arnold Hill Academy Page 9 of 25

 A girl jogs at 2.0 m s–1 in a straight line for 30 seconds, turns around and returns to her starting
8
point 20 seconds later.

What is her average velocity and average speed?

Average velocity/m s–1 Average speed/m s–1

A 0 m s−1 2.4 m s−1

B 0 m s−1 2.5 m s−1

C 1.0 m s−1 2.0 m s−1

D 2.5 m s−1 2.5 m s−1

(Total 1 mark)

A perfectly elastic rubber ball falls vertically from rest and rebounds from the floor. Which one of
9
the following velocity-time, v–t, graphs best represents the motion from the moment of release to
the top of the first rebound?

(Total 1 mark)

Arnold Hill Academy Page 10 of 25

 The velocity–time graph for a falling object is shown.
10

Which of the following shows the corresponding acceleration–time graph?

(Total 1 mark)

Arnold Hill Academy Page 11 of 25

 A body travels with speed v, which varies with time t as shown in the graph.
11

Which one of the graphs, A to D, shows how the distance s covered by the body varies with time
t?

(Total 1 mark)

Arnold Hill Academy Page 12 of 25

 The figure below is a speed-time graph for a sprinter at the start of a race.
12

Determine the distance covered by the sprinter in the first 0.3 s of the race.

_______________________________________________________________________

_______________________________________________________________________

_______________________________________________________________________

_______________________________________________________________________

_______________________________________________________________________

distance ______________________ m
(Total 3 marks)

A vehicle accelerates uniformly from a speed of 4.0 m s–1 to a speed of 12 m s–1 in 6.0 s.
13
(a) Calculate the vehicle's acceleration.

Acceleration ____________________
(2)

Arnold Hill Academy Page 13 of 25

 (b) On the axes below, draw a graph of speed against time for the vehicle covering the 6.0 s
period in which it accelerates.

(2)

(c) Calculate the distance travelled by the vehicle during its 6.0 s period of acceleration.

Distance ____________________
(2)
(Total 6 marks)

Galileo used an inclined plane, similar to the one shown in the figure below, to investigate the
14 motion of falling objects.

(a) Explain why using an inclined plane rather than free fall would produce data which is valid
when investigating the motion of a falling object.

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(2)

Arnold Hill Academy Page 14 of 25

(b) In a demonstration of Galileo’s investigation, the number of swings of a pendulum was
used to time a trolley after it was released from rest. A block was positioned to mark the
distance that the trolley had travelled after a chosen whole number of swings.
See the figure below.

The mass of the trolley in the figure above is 0.20 kg and the slope is at an angle of 1·8º to
the horizontal.

(i) Show that the component of the weight acting along the slope is about 0.06 N.

(2)

(ii) Calculate the initial acceleration down the slope.

answer = ______________________ m s–2

(2)

Arnold Hill Academy Page 15 of 25

(c) In this experiment, the following data was obtained. A graph of the data is shown below it.

time / pendulum swings distance travelled /m

1 0.29

2 1.22

3 2.70

4 4.85

From the graph above, state what you would conclude about the motion of the trolley?
Give a reason for your answer.

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________

___________________________________________________________________
(2)

Arnold Hill Academy Page 16 of 25

 (d) Each complete pendulum swing had a period of 1.4 s. Use the graph above to find the
speed of the trolley after it had travelled 3.0 m.

answer = ______________________ m s–1

(3)
(Total 11 marks)

A lunar landing module is descending to the Moon’s surface at a steady velocity of 10.0 m s –1. At
15
a height of 120 m a small object falls from its landing gear. Assuming that the Moon’s
gravitational acceleration is 1.60 m s–2, at what speed, in m s–1 does the object strike the Moon?

A 22.0

B 19.6

C 16.8

D 10.0

(Total 1 mark)

Arnold Hill Academy Page 17 of 25

Mark schemes
(a) (i) rate of change of velocity
1
[or a = ] (1)

(ii) (acceleration) has (magnitude and) direction (1)

2

(b) (i) (acceleration) is the gradient (or slope) of the graph (1)

(ii) (displacement) is the area (under the graph)

2

(c)

4
[8]

B
2
[1]

(a) (i) region A: uniform acceleration

3
(or (free-fall) acceleration = g (= 9.8(i) m s–2))

force acting on parachutist is entirely his weight

(or other forces are very small) (1)

(ii) region B: speed is still increasing

acceleration is decreasing (2) (any two)

because frictional (drag) forces become significant (at higher speeds)

(iii) region C: uniform speed (50 m s–1)

because resultant force on parachutist is zero (2) (any two)

weight balanced exactly by resistive force upwards

The Quality of Written Communication marks were awarded primarily for the
quality of answers to this part
(6)

Arnold Hill Academy Page 18 of 25

 (b) deceleration is gradient of the graph (at t = 13s) (1)

(e.g. 20/1 or 40/2) = 20 m s–2 (1)

(2)

(c) distance = area under graph (1)

suitable method used to determine area (e.g. counting squares) (1)
with a suitable scaling factor (e.g. area of each square = 5 m2) (1)
distance = 335 m (±15 m) (1)
(4)

(d) (i) speed = √(5.02 + 3.02) = 5.8 m s–1 (1)

(ii) tan θ = gives θ = 31° (1)

(2)
[14]

C
4 [1]

(a) correct substitution in (v2 = u2 + 2as)

5
or correct rearrangement g = or

= 9.6 (9.61 m s–1)

2

(b) g = W/m or W = mg (= ma) and weight is proportional

to mass/doubling the mass doubles the weight/’masses
cancel’/the factor of two cancels (so g remains the same)
1

(c) ball’s acceleration will decrease/be less than card’s or card’s

acceleration will be unaffected/nearly constant

air resistance affects cards less or card is more streamlined

or card does less work against air resistance
alternative timing/(velocity/speed/acceleration)
uncertain/(inaccurate /imprecise/less reliable)
indication that full width of ball may not pass through gate/difficulty
in determining ‘length’ of ball passing through gate
2
[5]

C
6
[1]

Arnold Hill Academy Page 19 of 25

 (a) (i) maximum distance from 1st to 5th image = 139 mm (allow 138 to 140mm) ✔
7
Any other correctly measured distance(s), to provide additional data, but do not allow
the distance from 1st to 2nd image (as this is too small).

Alternatively allow a repeat measurement of the maximum distance for this mark. ✔
E.g. 1st to 4th image distance = 79 mm, 1st to 3rd image distance =
34 mm (allow ± 1mm on these values)
If a candidate measures distances which do not go back to the first
image the initial velocity, u, will not be zero. Use of the ‘suvat’
equations is then considerably more complicated. A mark can still
be awarded, provided the candidate illustrates how g can be
calculated or correctly calculates g from this value in (a)(ii).
If the printing process in your centre alters the scale of this
diagram, measure the values on your printed papers and mark
the scripts accordingly. (Send details to the moderator).
If the candidate is visually impaired and is using a modified
paper that alters the scale of this diagram, measure the values
on the printed paper and mark the script accordingly.
2

(ii) Evidence of correct number of time intervals to match the distance used.(e.g Using
distance from 1st to 5th marble with 4 time intervals, time = 0.174 s) ✔

Value of g = 9.18 or 9.2 m s–2 (based on 139 mm and 0.174 s)

Allow ecf from value of time in (a),and ecf from incorrect
measurements in (b), but to allow ecf candidate must show
workings of the calculation and not just state a value for g

(Allow also 918 or 920 cm s–2 and 9180 or 9200 mm s –2) Answer must have correct
unit ✔
Allow this mark based on a correct calculation from just one
measurement of distance in (a)(i)
No sf penalty
2

(b) So image is sharp / less blurred / image is well defined

OR
Any answer referring to ‘motion blurring’
Allow reference to ‘image’ or ‘marble’
1
[5]

A
8 [1]

D
9
[1]

B
10 [1]

Arnold Hill Academy Page 20 of 25

 B
11
[1]

clear attempt to use area under graph/statement that distance is

12 equivalent to area under graph

C1

38 to 40 squares/1 square is equivalent to 0.05 m

C1

1.9 to 2.0 m

A1
[3]

13 (a) a = Δv / t
C1

1.3 m s–2
A1

(b) (0,4) and (6,12) both marked (accept axes wrong way round)
M1

joined by a straight line and axes labelled with quantity or unit

A1

(c) distance = area under graph or average speed × time

C1

48 m (47.9 m) ecf from (a) or (b)

A1
[6]

(a) any two from

14
freefall is too quick (any indication of slower motion) (1)

(Galileo had) no (accurate) method to time freefall (or valid

comment regarding timing of freefall or inclined plane) (1)

correct reference to air resistance or drag (not ‘wind’) (1)

max 2

(b) (i) 0.20 × 9.81 = 1.962 (N) (1)

(1.962 sin 1.8 =) 0.0616 or 0.062 seen (1) (allow 0.061)

(0.0628 for use of g = 10 gets 1 mark)
2

Arnold Hill Academy Page 21 of 25

 (ii) 0.06(16)/0.20

or use of a = F/m with a clearly identified force but not the weight

or g sinθ = g sin 1.8° (1)

0.31 (m s–2) (1) (0.308)

accept 0.3 or 0.30 correct answer only for second mark

or (a = 2s/t2)

= 2 × 0.29/1.42 (1) = 0.31 (1) or use of other values from table

2

(c) accelerating (1) (accept increasing speed, etc but not increasing
acceleration/quicker motion, etc)

greater distance for each additional swing (‘per unit time’ must be implied)
or gradient/ steepness/ slope increasing (1) (accept curves upwards)
2

(d) tangent used:

tangent drawn at 3.0 m ± 0.3 on graph (1)

their time from graph × 1.4 (1)

= 1.28 to 1.44 (m s–1) (1)

or suvat used:

use of v = or v = (u) + at with a from (b) (ii) (1)

(t =) 4.4 to 4.5 (s) (1)

(speed =) 1.3 to 1.4 (m s–1) (1)

3
[11]

A
15
[1]

Arnold Hill Academy Page 22 of 25

Examiner reports
Parts (a) and (b) produced good responses although a significant proportion of candidates did
1 concern themselves with rate of change of speed rather than velocity. Part (c) was less well
answered and proved to be a good discriminator as only the most able candidates were able to
sketch the correct graph.

In part (a) most candidates were able to interpret the graph correctly and almost all understood
3 why the parachutist reached constant terminal speed in region C of the graph. Although many
also understood and stated that the acceleration in region A was constant, few stated that this
was because the drag on the parachutist was negligible or much smaller than his weight.
Answers were generally well expressed and a mark of four or five was most common. A minority
of candidates, however, was quite incapable of using physics terms accurately and subsequently
scored few marks.

Many candidates understood that the acceleration in part (b) equalled the gradient of the line in
region D of the graph and arrived at a correct answer (although the unit of acceleration was often
given as −1). Candidates who used a = (ʋ − u) / t very often chose points off the straight section
of the graph and arrived at α value for a outside the acceptable range.

In part (c) many candidates ignored the graph and attempted to use an equation of uniform
acceleration to find the distance travelled. The majority, however, made some attempt to relate
distance to the area under the graph and most of these answers fell within the acceptable range.

Part (d) was most often correct, although in part (ii) many candidates inverted the tan function
and found the angle to the horizontal rather than the vertical.

This calculation proved to be very accessible, with 84% of students giving the correct answer. It
4 should be noted that, in a written paper, students who use the suvat equations would not get the
same credit as those who correctly equate GPE and KE, despite the two approaches giving the
same answer.

Most candidates gained full marks in part (a). A few performed a calculation using t = s/v, with
5 3.1 as the average speed. This gave a value for g twice the required size.

In part (b) correct answers should have included ‘weight is proportional to the mass and W/m =
g’, or ‘doubling the mass will double the weight and g will remain the same’ or similar. Many said
increasing m will increase W but this was not sufficient for the mark.

A large majority of candidates seemed to be familiar with the use of a light-gate to measure
velocity in part (c). Most said that air resistance would affect the ball more. However, very few
then went on to explain that the increased air resistance would reduce the acceleration. Many
said that air resistance ‘slows down’ the ball. They may be thinking, incorrectly, that the ball slows
down as it falls, or they may be indicating that the ball is slower than it would be if there were no
air resistance. Students therefore need to be able to describe the motion of an object in an
unambiguous manner, eg ‘when an object falls, the acceleration decreases due to air resistance’.

Few candidates were able to explain that the full diameter of the ball was unlikely to pass through
the beam. This is a difficult idea to express. Candidates should be encouraged to include a
simple sketch to help illustrate a point if they are finding it difficult to put into words. Some said
that that there is more uncertainty in the measurement of the diameter of the ball. However, this
would depend on the measurement technique, so credit could not be given.

Arnold Hill Academy Page 23 of 25

 This question discriminated well, with only the most able candidates scoring four or five marks.
7
(a) (i) Some candidates attempted to measure the largest distance, between the initial and
4th position. A tolerance of +/-1 mm was allowed on their measurement.

Fewer candidates attempted a second measurement, although the question clearly

referred to measurements
.

(ii) This proved to be much more difficult, and candidates had to compute the correct
time interval for the distance measured, and then use the correct formula. Only the
most able candidates were able to compute a correct value for g.

(b) Fewer than half of the candidates appreciated how the sharpness of the image would
depend on the duration of the flash.

Students should be warned about multiple-choice questions that have an apparently very
8 straightforward solution. Approximately the same number of students gave the incorrect
response B as gave the correct response in this question. Presumably they calculated the speed
for the second half of the journey, and took the average of the two speeds rather than calculating
the total distance divided by the total time.

Being able to interpret graphs is another important skill commonly tested by multiple choice
10 questions. 67% of students were able to spot that graph B correctly represented the variation of
the gradient of the velocity-time graph with time. The most popular distractor was A, perhaps due
to students eliminating C and D as being obviously incorrect, and being able to go no further.

Most candidates realised that they should determine the area under the graph. Techniques for
12 doing this varied, but square counting tended to be most accurate and less prone to error. The
standard of setting out of working was generally poor.

(a) This calculation was successfully done by the majority of candidates.

13
(b) The graph was adequately drawn by the majority of candidates.

(c) A few candidates made errors in this calculation by either using the maximum (rather than
average) value of speed or by making an incorrect assessment of the area under the
graph.

In part (a), candidates did not have to have encountered Galileo’s method for investigating
14 freefall to be successful. Many showed awareness that either air resistance would not be a
significant factor or that timing would be easier due to the lesser speeds when using an inclined
plane.

Considerably less than half candidates were able to resolve to find the component of the weight
acting down the slope in part (b) (i). Some used just the mass rather than mg and this response
gained zero marks.

Part (b) (ii) was a straight forward use of a = F/m and the majority of candidates gained full
marks.

Arnold Hill Academy Page 24 of 25

In part (c), many candidates thought the trolley was accelerating at an increasing rate because of
the upward curve. Some did not use the term ‘acceleration’ in their answer and some thought
that the rate of acceleration was decreasing because the curve was getting straighter. The data
plotted on the graph does not support the view that the acceleration decreases. The distance
between each pendulum swing increases in such a way to support uniform acceleration.

A very large majority of candidates did not recall that the gradient of a distance time graph gives
the speed in part (d). Most of these calculated the average speed using v = s/t with s = 3.0 and t
= 3.15 × 1.4 rather than the instantaneous speed at 3.0 m.

Arnold Hill Academy Page 25 of 25