Professional Documents
Culture Documents
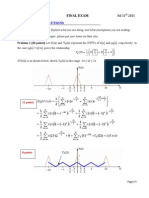
General Structure of Wave Mechanics (Ch. 5) : Product Dot DX U U U U J I X U Ions Eigenfunct
Uploaded by
Ronalson SiraitOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
General Structure of Wave Mechanics (Ch. 5) : Product Dot DX U U U U J I X U Ions Eigenfunct
Uploaded by
Ronalson SiraitCopyright:
Available Formats
P460 - math concepts 1
General Structure of Wave
Mechanics (Ch. 5)
Sections 5-1 to 5-3 review items covered previously
use Hermitian operators to represent observables (H,p,x)
eigenvalues of Hermitian operators are real and give the
expectation values
eigenvectors for different eigenvalues are orthogonal and
form a complete set of states
any function in the space can be formed from a linear series
of the eigenfunctions
some variables are conjugate (position, momentum) and one
can transform from one to the other and solve the problem in
eithers space
x d
x
i dx p p
e x u C t x
product dot dx u u u u j i
x u ions eigenf unct
op
iEt
N N
ij j i j i
i
o
) (
) ( ) , (
| |
) ( :
* *
/
*
c
c
= >= <
=
= >= >=< <
} }
P460 - math concepts 2
Notation
there is a very compact format (Dirac notation) that is often
used
|i> = |u
i
> = eigenfunction
<_,|> is a dot product between 2 function
|i><j| is an outer product (a matrix). For example a rotation
between two different basis
if an index is repeated there is an implied sum
operator projection n n
n n n C x u C x
product dot dx u u u u j i
x u ions eigenfunct
N N N
ij j i j i
i
= = =
= >= >=< <
}
o
) ( ) (
| |
) ( :
*
P460 - math concepts 3
Degeneracy (Ch. 5-4)
If two different eigenfunctions have the same eigenvalue they
are degenerate (related to density of states)
any linear combination will have the same eigenvalue
usually pick two linear combinations which are orthogonal
can be other operators which have only some specific linear
combinations being eigenfunctions. Choice may depend on
this (or on what may break the degeneracy)
example from V=0
) ( ) (
j i j i
j j i i
u u a u u O
au Ou au Ou
| o | o + = +
= =
0 ) ( : ,
0 cos sin : cos , sin
2
, , cos , sin
*
2 2
=
=
=
}
}
dx e e orthogonal e e
kxdx kx orthogonal kx kx
m
k
E e e kx kx
ikx ikx ikx ikx
ikx ikx
P460 - math concepts 4
Degeneracy (Ch. 5-4)
Parity and momentum operators do not commute
and so cant have the same eigenfunction
two different choices then depend on whether you want an
eigenfunction of Parity or of momentum
momentum e e
Parity kx kx
ikx ikx
,
cos , sin
P
x
i P p Pp p P
x
x
i x P p
x
x
i
x
x
i P x p P
op op op
op
op
c
c
= =
c
c
=
c
c
=
c
c
=
2 ] , [
) (
)) ( (
) (
)
) (
( )) ( (
P460 - math concepts 5
Uncertainty Relations
(Supplement 5-A)
If two operators do not commute then their uncertainty
product is greater then 0
if they do commute 0
start from definition of rms and allow shift so the functions
have <U>=0
define a function with 2 Hermitian operators A and B U
and V and real
because it is positive definite
can calculate I in terms of U and V and [U,V]
2 2
2 * 2 2 2 2
) ( ) ( , 0
) (
A U U A A U
dx A A A A A
A = A >= >< < =
>= < > < > =< A
}
) ( ) ( ) ( x V i U x | + =
0 ) (
*
> =
}
dx I | |
> < =
> < =
B B V
A A U
dx V i U V i U
dx V i U V i U
dx V i U V i U I
dag dag
) )( (
) )( (
) ( ) ) ((
*
*
*
+ =
+ =
+ + =
}
}
}
Hermitian
U U U
T dag
= =
*
P460 - math concepts 6
Uncertainty Relations
(Supplement 5-A)
rearrange
But just the expectation values
can ask what is the minimum of this quantity
use this uncertainty relationship from operators alone
dx V VU UV i U
dx V i U V i U I
) ) ( (
) )( (
2 2 2 *
*
+ + =
+ =
}
}
> < + > < + > =<
> < + > < > < + > =<
2 2 2
2 2 2
] , [
) (
V V U i U
V VU UV i U I
> <
> <
= =
2
min
2
] , [
0
V
V U i
d
dI
2 2 2
2 2 2
2 2
min min
2
min
] , [
4
1
) ( ) (
] , [
4
1
0 ] , [ ) (
> < > A A
> < > > >< <
> > < + > < + > =<
B A i B A
V U i V U
V V U i U I
P460 - math concepts 7
Uncertainty Relations -- Example
take momentum and position operators
in position space
that x and p dont commute, and the value of the commutator,
tells us directly the uncertainty on their expectation values
i x p xp px
x
x i i x
x
i px
x
x i xp
x
i p x x
op op
= =
c
c
=
c
c
=
c
c
=
c
c
= =
] , [
2
) (
2
1
] , [
4
1
] , [
4
1
) ( ) (
2 2
2 2 2
= > < = > < > A A
> < > A A
i i x p i x p
B A i B A
P460 - math concepts 8
Time Dependence of Operators
the Hamiltonian tells us how the expectation value for an
operator changes with time
but know Scrod. Eq.
and the H is Hermitian
and so can rewrite the expectation value
dx t x
t
A t x dx t x A t x
t
dx t x
t
A
t x A
dt
d
dx t x A t x A
t
t
)] , ( [ ) , ( ) , ( )] , ( [
) , ( ) , (
) , ( ) , (
* *
*
*
c
c
+
c
c
+
c
c
= > <
= > <
} }
}
}
* * *
*
)
1
(
1
H
i
H
i t
H
i t
= =
c
c
=
c
c
HA A H H H
T * * *
) ( = =
| | A H
i
t
A
A
dt
d
dx AH
i
dx HA
i
t
A
A
dt
d
t
t
t
t
,
* *
+
c
c
= > <
+
c
c
= > <
} }
P460 - math concepts 9
Time Dependence of Operators II
so in some sense just by looking at the operators (and not
necessarily solving S.Eq.) we can see how the expectation
values changes.
if A doesnt depend on t and [H,A]=0 <A> doesnt change
and its observable is a constant of the motion
homework has H(t); lets first look at H without t-dependence
and look at the t-dependence of the x expectation value
| | A H
i
t
A
A
dt
d
t
t
,
+
c
c
= > <
) (
2
2
x V
m
p
H + =
| |
| | | | | | | |
m
p
x
dt
d
p
i
p x p x p p x p x x V
x x V
m
p i
x H
i
x
dt
d
=
= + = =
(
+ = =
2
, , , 0 ), (
), (
2
,
2
2
P460 - math concepts 10
Time Dependence of Operators III
and look at the t-dependence of the p expectation value
rearrange giving
like you would see in classical physics
| |
| |
dx
dV
i dx
d
i
V V
dx
d
i
p V V p Vp pV
x V p
i
p x V
m
p i
p H
i
p
dt
d
= =
=
=
(
+ = =
) (
) ( ) ( ) (
) ( ,
), (
2
,
2
| |
dt
x dV
x
dt
d
m and
dt
x dV
p
dt
d
dx
dV
i
x V p
) (
) (
) ( ,
2
2
=
= =
You might also like
- Critical radius and nuclei calculations for homogeneous nucleation of copper and ironDocument7 pagesCritical radius and nuclei calculations for homogeneous nucleation of copper and ironGuilherme Dos Santos MoreiraNo ratings yet
- Comparative Statics and Derivatives ExplainedDocument20 pagesComparative Statics and Derivatives Explainedawa_caemNo ratings yet
- The Lax-Wendroff Technique for Solving Hyperbolic PDEsDocument13 pagesThe Lax-Wendroff Technique for Solving Hyperbolic PDEsSnehit Sanagar100% (1)
- Physics problem set explores quantum mechanicsDocument5 pagesPhysics problem set explores quantum mechanicsDaljot Singh KangNo ratings yet
- Lee Smolin - A Real Ensemble Interpretation of Quantum MechanicsDocument14 pagesLee Smolin - A Real Ensemble Interpretation of Quantum MechanicsGeorge OvermeireNo ratings yet
- Chap 1 Preliminary Concepts: Nkim@ufl - EduDocument20 pagesChap 1 Preliminary Concepts: Nkim@ufl - Edudozio100% (1)
- DOC-20240316-WA0026Document3 pagesDOC-20240316-WA0026Thisala BandaraNo ratings yet
- MAE 152 Computer Graphics For Scientists and Engineers: Splines and Bezier CurvesDocument76 pagesMAE 152 Computer Graphics For Scientists and Engineers: Splines and Bezier CurvesPrateek ChakrabortyNo ratings yet
- FEU Diliman - Economic Optimization I - Lecture NotesDocument6 pagesFEU Diliman - Economic Optimization I - Lecture NotesM.E. Foods, Inc.No ratings yet
- Lesson 1 - FunctionsDocument35 pagesLesson 1 - FunctionsQyndel Zach BiadoNo ratings yet
- TensorsDocument46 pagesTensorsfoufou200350% (2)
- Functions in EngineeringDocument35 pagesFunctions in EngineeringMegane LeeNo ratings yet
- Discrete Random Variables and Probability DistributionsDocument36 pagesDiscrete Random Variables and Probability DistributionskashishnagpalNo ratings yet
- Project 02: Simple Slope Static and Dynamic AnalysisDocument13 pagesProject 02: Simple Slope Static and Dynamic AnalysisJason YudhaNo ratings yet
- Complex Integration and Conformal TransformationsDocument43 pagesComplex Integration and Conformal TransformationsRathnaNo ratings yet
- Paper 23-A New Type Method For The Structured Variational Inequalities ProblemDocument4 pagesPaper 23-A New Type Method For The Structured Variational Inequalities ProblemEditor IJACSANo ratings yet
- Galerkin's Method in ElasticityDocument29 pagesGalerkin's Method in ElasticityAdari SagarNo ratings yet
- Technical Note - Autoregressive ModelDocument12 pagesTechnical Note - Autoregressive ModelNumXL ProNo ratings yet
- Solutions To Home Practice Test/Mathematics: Integral Calculus-2 HWT - 1Document12 pagesSolutions To Home Practice Test/Mathematics: Integral Calculus-2 HWT - 1varunkohliinNo ratings yet
- Probability Theory and Mathematical Statistics: Homework 2, Vitaliy PozdnyakovDocument13 pagesProbability Theory and Mathematical Statistics: Homework 2, Vitaliy PozdnyakovGarakhan TalibovNo ratings yet
- The Structure of Determining Matrices For A Class of Double - Delay Control SystemsDocument18 pagesThe Structure of Determining Matrices For A Class of Double - Delay Control SystemsinventionjournalsNo ratings yet
- Linearna Algebra - Rjesenja, ETFDocument44 pagesLinearna Algebra - Rjesenja, ETFmarkovukNo ratings yet
- Y_d(Ω) sketch for problem 1Document4 pagesY_d(Ω) sketch for problem 1Le HuyNo ratings yet
- A New Non-Symmetric Information Divergence ofDocument7 pagesA New Non-Symmetric Information Divergence ofInternational Journal of Research in Engineering and TechnologyNo ratings yet
- Chapter 2 Mat455Document36 pagesChapter 2 Mat455Ajaq 98No ratings yet
- MECH300H Introduction To Finite Element Methods: ReviewDocument10 pagesMECH300H Introduction To Finite Element Methods: ReviewamitaiiscNo ratings yet
- Exam 2solutionDocument5 pagesExam 2solutionJames Steven HaneyNo ratings yet
- 2 Overview of Numerical AnalysisDocument59 pages2 Overview of Numerical AnalysisVashish RamrechaNo ratings yet
- 19 MacCormack TechniqueDocument14 pages19 MacCormack TechniquekkkrajaNo ratings yet
- PHY103A: Lecture # 2: Semester II, 2017-18 Department of Physics, IIT KanpurDocument21 pagesPHY103A: Lecture # 2: Semester II, 2017-18 Department of Physics, IIT KanpurSABARI BALANo ratings yet
- MATLAB FormulasDocument3 pagesMATLAB FormulasRoberto Alessandro IonescuNo ratings yet
- Ee 704 - Control Systems Ii Anith Krishnan 1Document13 pagesEe 704 - Control Systems Ii Anith Krishnan 1Anith KrishnanNo ratings yet
- Mathematics For Microeconomics: Maximization of A Function of One VariableDocument35 pagesMathematics For Microeconomics: Maximization of A Function of One VariableYbnias GrijalvaNo ratings yet
- 2nd Basiccal Differentiation RulesDocument35 pages2nd Basiccal Differentiation RulesBernadette BaduaNo ratings yet
- Vector Integral Calculus OutlineDocument65 pagesVector Integral Calculus OutlineTarek Hajj ShehadiNo ratings yet
- CFD Lecture 3: Dr. Thomas J. BarberDocument24 pagesCFD Lecture 3: Dr. Thomas J. BarberTareq DahbNo ratings yet
- EE644 - Discrete Time Systems Spring 2009 Midterm Exam #2 With Solutions Problem 1. Polyphase RepresentationsDocument5 pagesEE644 - Discrete Time Systems Spring 2009 Midterm Exam #2 With Solutions Problem 1. Polyphase RepresentationsDecker JamesNo ratings yet
- ROOT FINDINGDocument3 pagesROOT FINDINGyana22No ratings yet
- Mechanics of Solids Week 10 LecturesDocument9 pagesMechanics of Solids Week 10 LecturesFlynn GouldNo ratings yet
- Conversion Between State Space and Transfer Function Representations in Linear Systems - IDocument28 pagesConversion Between State Space and Transfer Function Representations in Linear Systems - ITeja VaitlaNo ratings yet
- Ufabccapitulo 1Document121 pagesUfabccapitulo 1Leonardo De Avellar FredericoNo ratings yet
- High Voltage Engineering Lec2Document14 pagesHigh Voltage Engineering Lec2nasirvivacNo ratings yet
- Equation Appendix Final ExamDocument5 pagesEquation Appendix Final ExamDhanush raoNo ratings yet
- Discrete-Time Signals and SystemsDocument111 pagesDiscrete-Time Signals and Systemsduraivel_anNo ratings yet
- Process Modelling and OptimizationDocument11 pagesProcess Modelling and Optimizationavish mehtaNo ratings yet
- Interpolation Produces That Matches Exactly. The Function Then Can Be Utilized To ApproximateDocument44 pagesInterpolation Produces That Matches Exactly. The Function Then Can Be Utilized To ApproximategraphicalguruNo ratings yet
- Lecture 4 (Compatibility Mode)Document26 pagesLecture 4 (Compatibility Mode)Anonymous dGnj3bZNo ratings yet
- 2nd Basiccal Differentiation RulesDocument35 pages2nd Basiccal Differentiation RulesBernadette BaduaNo ratings yet
- Mech300H Introduction To Finite Element Methods: Finite Element Analysis (F.E.A.) of 1-D ProblemsDocument31 pagesMech300H Introduction To Finite Element Methods: Finite Element Analysis (F.E.A.) of 1-D Problemsbadboys123No ratings yet
- Advanced Computational Methods: Numerical IntegrationDocument59 pagesAdvanced Computational Methods: Numerical IntegrationMohammed HamdyNo ratings yet
- Some Basic Formulae:: Quadratic FormulaDocument6 pagesSome Basic Formulae:: Quadratic FormulaBlazingStudiosNo ratings yet
- AM I MID TERM EXAMINATION (ECEA and ECE B) 2-3-2022Document16 pagesAM I MID TERM EXAMINATION (ECEA and ECE B) 2-3-2022Ruag ShradaNo ratings yet
- Discrete Signals and SystemsDocument111 pagesDiscrete Signals and SystemsharivarahiNo ratings yet
- Paper 6Document9 pagesPaper 6RakeshconclaveNo ratings yet
- Motilal Nehru National Institute of Technology Civil Engineering Department Least Square Regression Curve FittingDocument44 pagesMotilal Nehru National Institute of Technology Civil Engineering Department Least Square Regression Curve Fittingvarunsingh214761No ratings yet
- Correlation and Regression AnalysisDocument23 pagesCorrelation and Regression AnalysisMichael EdwardsNo ratings yet
- Inverse Trigonometric Functions (Trigonometry) Mathematics Question BankFrom EverandInverse Trigonometric Functions (Trigonometry) Mathematics Question BankNo ratings yet
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesFrom EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesNo ratings yet
- Application of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsFrom EverandApplication of Derivatives Tangents and Normals (Calculus) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- Transformation of Axes (Geometry) Mathematics Question BankFrom EverandTransformation of Axes (Geometry) Mathematics Question BankRating: 3 out of 5 stars3/5 (1)
- BUKU INTI-bfm:978-1-4613-9907-0/1 BUKU PDFDocument13 pagesBUKU INTI-bfm:978-1-4613-9907-0/1 BUKU PDFRonalson SiraitNo ratings yet
- CH 15Document53 pagesCH 15Ronalson SiraitNo ratings yet
- chapter2MPF2012 PDFDocument80 pageschapter2MPF2012 PDFRonalson SiraitNo ratings yet
- 8 Power Considerations and The Poynting VectorDocument10 pages8 Power Considerations and The Poynting VectorMuhammad SaadNo ratings yet
- BUKU INTI-bfm:978-1-4613-9907-0/1 BUKU PDFDocument13 pagesBUKU INTI-bfm:978-1-4613-9907-0/1 BUKU PDFRonalson SiraitNo ratings yet
- Chem 373 - Lecture 17: Radial Wavefunction and Orbital Levels of The Hydrogen AtomDocument21 pagesChem 373 - Lecture 17: Radial Wavefunction and Orbital Levels of The Hydrogen AtomNuansak3100% (1)
- How To Report and Use UncertaintiesDocument22 pagesHow To Report and Use UncertaintiesRonalson SiraitNo ratings yet
- Measurement & Uncertainties: Dosen PengampuDocument26 pagesMeasurement & Uncertainties: Dosen PengampuRonalson SiraitNo ratings yet
- HCPDocument4 pagesHCPIshan BaruahNo ratings yet
- 8 Power Considerations and The Poynting VectorDocument10 pages8 Power Considerations and The Poynting VectorMuhammad SaadNo ratings yet
- Christopher Chui: 6/5/2014 Nuclear Chemistry - C. Chui 1Document11 pagesChristopher Chui: 6/5/2014 Nuclear Chemistry - C. Chui 1Ronalson SiraitNo ratings yet
- Emulsi Pada Produk SusuDocument28 pagesEmulsi Pada Produk SusuRonalson SiraitNo ratings yet
- Nuclear LectureDocument35 pagesNuclear LectureRonalson SiraitNo ratings yet
- 1 Pengantar MekatronikaDocument64 pages1 Pengantar MekatronikaRonalson SiraitNo ratings yet
- Deterministic ModelsDocument1 pageDeterministic ModelsRonalson SiraitNo ratings yet
- Bab 3 Pengantar Inferensi StatistikaDocument46 pagesBab 3 Pengantar Inferensi StatistikaRonalson SiraitNo ratings yet
- k1 0Document19 pagesk1 0Ronalson SiraitNo ratings yet
- Introduction To Quantum Field TheoryDocument261 pagesIntroduction To Quantum Field TheorykoutariNo ratings yet
- Organic Chemistry With Biological Applications 3rd Edition Mcmurry Test BankDocument9 pagesOrganic Chemistry With Biological Applications 3rd Edition Mcmurry Test BankCarolHutchinsonmrwjn100% (11)
- EpiGaN-HV650V Leaflet Feb 2017Document2 pagesEpiGaN-HV650V Leaflet Feb 2017Quan LinhNo ratings yet
- Test OdtDocument4 pagesTest OdtkanwaljitsinghchanneyNo ratings yet
- Esc201: Introducton To Electronics: DiodesDocument35 pagesEsc201: Introducton To Electronics: Diodesash jayNo ratings yet
- Junction Field Effect TransistorDocument3 pagesJunction Field Effect TransistorAbril de VeraNo ratings yet
- Makalah Metalurgi Fisik HCPDocument6 pagesMakalah Metalurgi Fisik HCPAdlan MizanNo ratings yet
- Physics Solution: Electric Field and ChargesDocument10 pagesPhysics Solution: Electric Field and ChargesTrilok AkhaniNo ratings yet
- ME280 Homework #2: Problem SolutionsDocument9 pagesME280 Homework #2: Problem Solutions104922No ratings yet
- Adsorption For Wastewater Treatment and Water Purification: Basic Knowledge On Adsorption Process and Types of AdsorbentsDocument16 pagesAdsorption For Wastewater Treatment and Water Purification: Basic Knowledge On Adsorption Process and Types of AdsorbentsHenryPeñaNo ratings yet
- Multiple Particle SystemsDocument21 pagesMultiple Particle SystemsMD IMRAN HOSSENNo ratings yet
- CH 3 Crystalline StructuresDocument71 pagesCH 3 Crystalline StructuresMusab AbdrabbuhNo ratings yet
- Thompson PDFDocument50 pagesThompson PDFYudi FernandezNo ratings yet
- Introduction To CeramicsDocument3 pagesIntroduction To CeramicsHarini MunasingheNo ratings yet
- Atomic Structure MCQS: 1 Year N0tes Chemistry NewDocument11 pagesAtomic Structure MCQS: 1 Year N0tes Chemistry NewHaider Jalal100% (9)
- Ternary Phase DiagramsDocument10 pagesTernary Phase DiagramsJéssica NotórioNo ratings yet
- Metallurgy MMS Module 1 and 2Document245 pagesMetallurgy MMS Module 1 and 2Sahal T YousephNo ratings yet
- 2017 9646 H2 Physics Prelim Paper 2 SolutionDocument10 pages2017 9646 H2 Physics Prelim Paper 2 SolutionxiaokiaNo ratings yet
- Icondugtivity: MaterlalsDocument6 pagesIcondugtivity: MaterlalsSakshi KabadeNo ratings yet
- The Value of Surface Tension of A Liquid at Critical Temperature IsDocument10 pagesThe Value of Surface Tension of A Liquid at Critical Temperature Issagarchidre114No ratings yet
- Organic Solar CellsDocument21 pagesOrganic Solar CellsTôn Vương NguyễnNo ratings yet
- Superconductivity in Twisted Bilayer GrapheneDocument19 pagesSuperconductivity in Twisted Bilayer GrapheneScience BrainsNo ratings yet
- Problem Set 5Document2 pagesProblem Set 5Saied Aly SalamahNo ratings yet
- Solution Set 3Document11 pagesSolution Set 3HaseebAhmadNo ratings yet
- Colloidal System: by Msc. Dua'A M. HadiDocument22 pagesColloidal System: by Msc. Dua'A M. HadiYahya Daham Zafeer SakhrNo ratings yet
- Single Electron Tunneling DevicesDocument16 pagesSingle Electron Tunneling DevicesDebapriya Basu RoyNo ratings yet
- Magnetic Domain Wall StructureDocument21 pagesMagnetic Domain Wall StructureGuille AngonaNo ratings yet