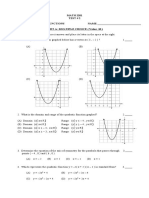
Quadratic Curves

4.3  Quadratic Curves

 • Supply, demand, cost, revenue, and profit
functions can also be quadratic curves.
• Examples:
S(x)  x  30x
2
D(x)  x 2 100x  2,400

• Quadratic curves – plane curves with

equations of the form
2
Ax  Bxy  Cy  Dx  Ey  F  0
2

• These curves are called conic sections.

 4.3  Quadratic Curves

• Types: Circle, Ellipse, Parabola, Hyperbola

• For more information, read Section 3.2 of the

book.
4.3  Quadratic Curves
1. Given the supply function S(x) = x2 + 6x + 9
and demand function D(x) = x2 – 10x + 25,
find the market equilibrium quantity and
price.
S(x)  D(x)
x 2  6x  9  x 2 10x  25
x 1

S(1)
 12
 6(1)  9 16
: 1 unit
m.e. quantity m.e. price : Php16

4.3  Quadratic Curves

 7. Given the demand function yD(x + 4) = 400
and supply function 2yS – x – 38 = 0, find the
market equilibrium quantity and price.
yS  yD
x  38
yS  400 x  38
2 
400 x4 2
yD 
x4  800  (x  38)(x  4)
x 2  42x  648  0
 x  12
y S (12)  1238
2  25 

m.e. quantity : 12 units m.e. price : Php25

 4.3  Quadratic Curves
 9. Given the cost function C(x) = 1,250 + 20x
and revenue function R(x) = x(50 – 0.1x), find
the break-even quantity and price.

C(x)  R(x) C(50)  2,250

1,250  20x  50x  0.1x 2 C(250)  6,250

x 2  300x 12,500  0
 
x  50 or x  250 

 b.e. points : (50,2250) and (250,6250)


4.3  Quadratic Curves


19. When a particular computer accessory is
sold for x pesos per unit, manufacturers will
2
supply 10 units to local retailers. The local
x

demand would be 60 – x units.

a)At what market price will the manufacturers'
supply of the items be equal to the

consumers' demand for them?
b)How many units will be sold at this price?

4.3  Quadratic Curves

 S(x)  D(x)
x2
 60  x
10
 x 10x  600  0
2

(x  30)(x  20)  0

x  20


 D(20)  60  20  Php40


4.3  Quadratic Curves


25. Assume that a company's cost and revenue
functions are C(x) = 6x + 120 and
R(x) = 3x2+48x, respectively.
a)Find the break-even price and quantity.
b)Set up the profit function and use it to find the
profit when 120 units are manufactured and
sold.

4.3  Quadratic Curves

 25. Assume that a company's cost and revenue
functions are C(x) = 6x + 120 and
R(x) = 3x2+48x, respectively.
a)Find the break-even price and quantity.
C(x)  R(x)
6x 120  3x 2  48x C (2.43)  134.58
3x 2  42x 120  0
C (3)  138.00
 x 2 14 x  40  0

x  2.43

x3 b.e. price : Php138.00
 b.e. quantity : 3 units

4.3  Quadratic Curves

 25. Assume that a company's cost and revenue
functions are C(x) = 6x + 120 and
R(x) = 3x2+48x, respectively.
b)Set up the profit function and use it to find the
profit when 120 units are manufactured and
sold.
P(x)  R(x)  C(x)  (3x 2  48x)  (6x 120)
 3x 2  42x 120

 P(120)  3(120)

2
 42(120) 120  Php48,120

4.3  Quadratic Curves
