Professional Documents
Culture Documents
Calculus Assignment 1
Uploaded by
kibet caleb0 ratings0% found this document useful (0 votes)
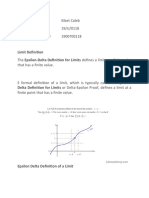
4 views9 pages1. The document defines the epsilon-delta definition of limits, which defines a limit at a finite point that has a finite value. It introduces the variables epsilon and delta and explains how they are used to define regions around the limit point.
2. The document works through two examples of applying the epsilon-delta definition of limits. The first example finds the limit as x approaches 2 of 3x+5, showing that the limit is 11. The second example finds the limit as x approaches 1 of 1/x, showing that the limit is 3.
3. In both examples, delta is chosen in terms of epsilon to satisfy the epsilon-delta definition. Calculations are shown to demonstrate that for any epsilon
Original Description:
Original Title
Calculus assignment 1 (1)
Copyright
© © All Rights Reserved
Available Formats
PPTX, PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Document1. The document defines the epsilon-delta definition of limits, which defines a limit at a finite point that has a finite value. It introduces the variables epsilon and delta and explains how they are used to define regions around the limit point.
2. The document works through two examples of applying the epsilon-delta definition of limits. The first example finds the limit as x approaches 2 of 3x+5, showing that the limit is 11. The second example finds the limit as x approaches 1 of 1/x, showing that the limit is 3.
3. In both examples, delta is chosen in terms of epsilon to satisfy the epsilon-delta definition. Calculations are shown to demonstrate that for any epsilon
Copyright:
© All Rights Reserved
Available Formats
Download as PPTX, PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
4 views9 pagesCalculus Assignment 1
Uploaded by
kibet caleb1. The document defines the epsilon-delta definition of limits, which defines a limit at a finite point that has a finite value. It introduces the variables epsilon and delta and explains how they are used to define regions around the limit point.
2. The document works through two examples of applying the epsilon-delta definition of limits. The first example finds the limit as x approaches 2 of 3x+5, showing that the limit is 11. The second example finds the limit as x approaches 1 of 1/x, showing that the limit is 3.
3. In both examples, delta is chosen in terms of epsilon to satisfy the epsilon-delta definition. Calculations are shown to demonstrate that for any epsilon
Copyright:
© All Rights Reserved
Available Formats
Download as PPTX, PDF, TXT or read online from Scribd
You are on page 1of 9
Calculus assignment 1
Name : Kibet Caleb
Student number : 19/U/0118
Registration number : 1900700118
Limit Definition
• The Epsilon-Delta Definition for Limits defines a limit at a
finite point that has a finite value.
•
• The formal definition of a limit, which is typically called
the Epsilon-Delta Definition for Limits or Delta-Epsilon Proof,
defines a limit at a finite point that has a finite value.
Limit definition
Limit definition
• First, we create two variables, delta (δ) and epsilon (ε).
• Next we choose an epsilon region around the number L on the y-
axis.
• Then, we use this region to help us define a delta region around
the number a on the x-axis so that all x-values, excluding a, inside
the region correspond to y-values inside the epsilon region.
• Finally, we show (prove) that we can find y-values of the function
as close as we want to the value L by using only the points in a
small enough interval around a.
• We will define our limit in such a way as to allow epsilon to
represent any number, while we restrict the value of delta; thus,
ensuring that our region is precise.
1. lim (3 𝑥 +5 )=11
𝑥 →2
• Solution
• Let ε > 0.
• The first part of the definition begins “For every ε > 0.” This means
we must prove that whatever follows is true no matter what
positive value of ε is chosen. By stating “Let ε > 0,” we signal our
intent to do so.
• Choose δ= ε/2.
• The definition continues with “there exists a δ > 0. ”. In other
words, we must go and find δ. So, where exactly did δ=ε/2 come
from?
• We tackle the problem from an algebraic point of view. This is our
"Analysis Doodle" to discover what value to use for δ.
1. lim 3 𝑥 +5=11
𝑥 →2
• Let ε > 0.
• Choose δ = ε/2.
• Assume 0 < |x−1| < δ.
• In other words:
• 0 < |x−1| < ε/2,
• so – ε/2 < x−1 < ε/2,
• then –ε < 2x−2 < ε
• then |2x−2| < ε,
• then |(3x+5)−11| < ε
• Thus, if 0 < |x−1| < δ, then |(3x+5)−11| < ε.
• Therefore, by the definition of limit, = 11
2. = 3
• The first part we separate the equations according to
the properites of limits
• Thus wee get
• =3
• ≠0
• As noted in the statement we only need to worry
about the limit in the denominator being zero when
we do the limit of a quotient. If it were zero we would
end up with a division by zero error and we need to
avoid that.
2. = 3
• 1. Let ε > 0.
• 2. Choose δ = min {1, ε/4}.
• This choice of δ may appear odd at first glance, but it
was obtained by taking a look at our ultimate desired
inequality:
• ∣ () −3 (∣ < ε.
• | ()| < ε.
• This inequality is equivalent to ||⋅|| < ε.
• This is the place where assuming δ ≤ 1 comes into play.
2. = 3
• The choice of δ ≤ 1 here is arbitrary. We could have just as easily used any other positive number.
• In some proofs, greater care in this choice may be necessary.
• Now, since δ ≤ 1 and |x - 1| < δ ≤ 1,
• We are able to show that |3x−3| <4.
• Consequently, ||⋅||<||⋅4
• At this point we realize that we also need δ ≤ ε/4.
• Thus, we choose δ = min {1, ε/4}.
• 3. Assume 0< || < δ. Thus,
• ||<1
• And
• || < ε/4.
•
• Since || < 1, we may conclude that −1 < < 1.
• Thus, by subtracting 3 from all parts of the inequality, we obtain – 4 < x−4 < −1. Consequently, |3x−3| < 4. This gives
us
• ∣∣ = ||⋅|| < ⋅4 = ε.
• Therefore,
•
• =3
You might also like
- Attacking Problems in Logarithms and Exponential FunctionsFrom EverandAttacking Problems in Logarithms and Exponential FunctionsRating: 5 out of 5 stars5/5 (1)
- Calculus Assignment 1Document7 pagesCalculus Assignment 1kibet calebNo ratings yet
- Week 5 The Precise Definition of A LimitDocument10 pagesWeek 5 The Precise Definition of A LimitCynthia PlazaNo ratings yet
- Chapter 2, Section 2.4: The Integers and DivisionDocument18 pagesChapter 2, Section 2.4: The Integers and Divisiontalhaaftab728No ratings yet
- 12limits NotesDocument17 pages12limits NotesAulia Diva Muthiah YudaNo ratings yet
- Epsilon Delta ProofsDocument2 pagesEpsilon Delta ProofsMrDubsterNo ratings yet
- The Epsilon-Delta Limit Definition:: A Few ExamplesDocument15 pagesThe Epsilon-Delta Limit Definition:: A Few ExamplesElvisNo ratings yet
- Evaluation of Definite IntegralDocument4 pagesEvaluation of Definite Integralapi-127466285No ratings yet
- Proving InequalitiesDocument4 pagesProving InequalitieskukumaluXDNo ratings yet
- Functions, Limtis and Continuity (Part 1)Document20 pagesFunctions, Limtis and Continuity (Part 1)NiñaLeizylMendezNo ratings yet
- 2.3 - LimitsDocument7 pages2.3 - LimitsJosephp22No ratings yet
- Error Analysis: - Significant Figures: The Number of Digits That Can Be Used With ConfidenceDocument38 pagesError Analysis: - Significant Figures: The Number of Digits That Can Be Used With Confidencedesigncrafthub.burhanNo ratings yet
- Inverse Tigonometric Functions PPT BenitezDocument42 pagesInverse Tigonometric Functions PPT BenitezAliyah Monique BenitezNo ratings yet
- Example: Problem 2.4.30 Definition of A Limit: 110.109 Calculus I (Phys Sci & Eng) Professor Richard BrownDocument2 pagesExample: Problem 2.4.30 Definition of A Limit: 110.109 Calculus I (Phys Sci & Eng) Professor Richard BrownAnilkumarsanctumNo ratings yet
- "Less Than" Absolute-Value InequalitiesDocument4 pages"Less Than" Absolute-Value InequalitiesWei JernNo ratings yet
- Numerical CH OneDocument45 pagesNumerical CH OneEbisa DugoNo ratings yet
- Numerical CH OneandtwoDocument25 pagesNumerical CH OneandtwoEbisa DugoNo ratings yet
- Kelompok 3-2Document14 pagesKelompok 3-2Abah Gamer1No ratings yet
- Quant Notes by Target 760Document8 pagesQuant Notes by Target 760francescoabcNo ratings yet
- Rational Numbers: 1.5 Is A Rational Number Because 1.5 3/2 (3 and 2 Are Both Integers)Document22 pagesRational Numbers: 1.5 Is A Rational Number Because 1.5 3/2 (3 and 2 Are Both Integers)Ethan MartinezNo ratings yet
- Ib Academy Math Studies Study GuideDocument64 pagesIb Academy Math Studies Study GuideSuuz de Bruijn100% (11)
- 3 5 PDFDocument21 pages3 5 PDFMahmoud Abdel-SalamNo ratings yet
- Continued FractionsDocument13 pagesContinued FractionsIonescu ViorelNo ratings yet
- 3 Limit and Continuity: 3.1 Definition of LimitsDocument94 pages3 Limit and Continuity: 3.1 Definition of LimitsDanmin TesfaNo ratings yet
- 3 Limit and Continuity: 3.1 Definition of LimitsDocument94 pages3 Limit and Continuity: 3.1 Definition of LimitsDanmin TesfaNo ratings yet
- 03 Integration MethodsDocument15 pages03 Integration MethodsJohn ReynielNo ratings yet
- 2020 State Competition SolutionsDocument13 pages2020 State Competition SolutionsSam LNo ratings yet
- Section 3 - Divisibility: - Definition: If N and D Are Integers and D 0, Then Integer K. - Alternatively, We SayDocument9 pagesSection 3 - Divisibility: - Definition: If N and D Are Integers and D 0, Then Integer K. - Alternatively, We SayNeeraj RanjanNo ratings yet
- 4-Absolute Value InequalityDocument19 pages4-Absolute Value Inequalitykimi no udinNo ratings yet
- Statistics Chapter-IVDocument59 pagesStatistics Chapter-IVMiley GirmayNo ratings yet
- Applied 1 ch3 2020Document25 pagesApplied 1 ch3 2020awelNo ratings yet
- Numerical Methods - Exercises: Introductory LectureDocument37 pagesNumerical Methods - Exercises: Introductory LectureFresh BarleyNo ratings yet
- Precise Definition of The LimitDocument5 pagesPrecise Definition of The LimitHades LucianNo ratings yet
- Absolute Value FunctionsDocument8 pagesAbsolute Value Functionsapi-357579360No ratings yet
- Epsilon Delta Proof of Sinx Over XDocument11 pagesEpsilon Delta Proof of Sinx Over Xlotto20012002100% (1)
- Lecture 3-EquationsDocument30 pagesLecture 3-EquationsLame JoelNo ratings yet
- Number System Class 9Document17 pagesNumber System Class 9gaurav nangru100% (1)
- Maths Real Numbers PPT by Aarushi PatidarDocument22 pagesMaths Real Numbers PPT by Aarushi PatidarAarushi PatidarNo ratings yet
- Basic Algebra LectureDocument95 pagesBasic Algebra Lecturericardo mccurchinNo ratings yet
- Mathslide 2Document41 pagesMathslide 2Phenicia De PeizaNo ratings yet
- Chapter 1: Divisibility & PrimesDocument25 pagesChapter 1: Divisibility & PrimesYue HUNo ratings yet
- Lect 3 ErrorsDocument5 pagesLect 3 ErrorsAlaa FjNo ratings yet
- Lecture 1 - Mathematical Preliminaries (Differentiation, Integration and Taylor Series)Document22 pagesLecture 1 - Mathematical Preliminaries (Differentiation, Integration and Taylor Series)Huzaika MatloobNo ratings yet
- Lecture 1: Limits, Derivatives, The Product Rule, The Quotient Rule, and The Chain RuleDocument41 pagesLecture 1: Limits, Derivatives, The Product Rule, The Quotient Rule, and The Chain RuleLevi LeuckNo ratings yet
- Exponentsexponents The Mathematicians ShorthandDocument29 pagesExponentsexponents The Mathematicians ShorthandJhon Ryan AlmendarezNo ratings yet
- Section 2-10: The Definition of The Limit - Practice Problems SolutionsDocument2 pagesSection 2-10: The Definition of The Limit - Practice Problems SolutionsDalmi G. SantosNo ratings yet
- Calculus Course 1Document3 pagesCalculus Course 1Abhijit Kar Gupta100% (2)
- Quest HW1 SolutionsDocument6 pagesQuest HW1 Solutionsellie<3No ratings yet
- Week 1-2Document33 pagesWeek 1-2DavisNo ratings yet
- Rootfindings 2ndstudentDocument19 pagesRootfindings 2ndstudentজোবায়ের মারুফNo ratings yet
- Klompok 6 422-425Document5 pagesKlompok 6 422-425radhiahhanifaturNo ratings yet
- Squares and Square RootsDocument8 pagesSquares and Square RootsJessica RamerNo ratings yet
- DS Lecture-10 Num THDocument34 pagesDS Lecture-10 Num THZaraNo ratings yet
- Section 9.1: Sequences Section 9.2: Infinite SeriesDocument51 pagesSection 9.1: Sequences Section 9.2: Infinite SeriesBerk GüneşNo ratings yet
- Chapter-2: Algorithms, Integers and MatricesDocument72 pagesChapter-2: Algorithms, Integers and MatricesSINIGI RAMYA SRINo ratings yet
- Junior/Intermediate Number Theory Tips: A B A BDocument9 pagesJunior/Intermediate Number Theory Tips: A B A BpantmukulNo ratings yet
- Daily Productivity TemplateDocument1 pageDaily Productivity Templatekibet calebNo ratings yet
- Assignment 1-Formal Definition of Limits1Document1 pageAssignment 1-Formal Definition of Limits1kibet calebNo ratings yet
- 50+ Best Web Development Tools and Resources PDFDocument20 pages50+ Best Web Development Tools and Resources PDFkibet calebNo ratings yet
- Javascript Array Methods Ebook PDFDocument34 pagesJavascript Array Methods Ebook PDFkibet calebNo ratings yet
- Developer S Handbook 6XeUxslA PDFDocument3 pagesDeveloper S Handbook 6XeUxslA PDFkibet calebNo ratings yet
- Chapter 16 - Logical Database DesignDocument33 pagesChapter 16 - Logical Database Designkibet calebNo ratings yet
- Chapter 17 - Physical Database DesignDocument44 pagesChapter 17 - Physical Database Designkibet calebNo ratings yet
- EERD Discussion Case StudyDocument1 pageEERD Discussion Case Studykibet calebNo ratings yet
- Mountain View Community HospitalDocument1 pageMountain View Community Hospitalkibet calebNo ratings yet
- DATA AND INFORMATION MANAGEMENT AssignmenrtDocument5 pagesDATA AND INFORMATION MANAGEMENT Assignmenrtkibet calebNo ratings yet
- Your Free Buyer Persona TemplateDocument8 pagesYour Free Buyer Persona Templateel_nakdjoNo ratings yet
- Final PS-37 Election Duties 06-02-24 1125pm)Document183 pagesFinal PS-37 Election Duties 06-02-24 1125pm)Muhammad InamNo ratings yet
- Simple Future Tense & Future Continuous TenseDocument2 pagesSimple Future Tense & Future Continuous TenseFarris Ab RashidNo ratings yet
- WO 2021/158698 Al: (10) International Publication NumberDocument234 pagesWO 2021/158698 Al: (10) International Publication Numberyoganayagi209No ratings yet
- Equine PregnancyDocument36 pagesEquine Pregnancydrdhirenvet100% (1)
- Spiritual Transcendence in Transhumanism PDFDocument10 pagesSpiritual Transcendence in Transhumanism PDFZeljko SaricNo ratings yet
- Marketing PlanDocument41 pagesMarketing PlanMark AbainzaNo ratings yet
- Focus Charting of FDocument12 pagesFocus Charting of FRobert Rivas0% (2)
- Jesus Died: Summary: Jesus Died We Need To Have No Doubt About That. Without Jesus' Death We Would Have NoDocument6 pagesJesus Died: Summary: Jesus Died We Need To Have No Doubt About That. Without Jesus' Death We Would Have NoFabiano.pregador123 OliveiraNo ratings yet
- Contents Serbo-Croatian GrammarDocument2 pagesContents Serbo-Croatian GrammarLeo VasilaNo ratings yet
- A Passage To AfricaDocument25 pagesA Passage To AfricaJames Reinz100% (2)
- Large Span Structure: MMBC-VDocument20 pagesLarge Span Structure: MMBC-VASHFAQNo ratings yet
- Essay EnglishDocument4 pagesEssay Englishkiera.kassellNo ratings yet
- Clinincal Decision Support SystemDocument10 pagesClinincal Decision Support Systemم. سهير عبد داؤد عسىNo ratings yet
- Percy Bysshe ShelleyDocument20 pagesPercy Bysshe Shelleynishat_haider_2100% (1)
- Concentrating Partial Entanglement by Local OperationsDocument21 pagesConcentrating Partial Entanglement by Local OperationsbhpliaoNo ratings yet
- Peri Operative Nursing ManagementDocument19 pagesPeri Operative Nursing ManagementSabina KontehNo ratings yet
- War Thesis StatementsDocument8 pagesWar Thesis StatementsHelpPaperRochester100% (2)
- The Minecraft Survival Quest ChallengeDocument4 pagesThe Minecraft Survival Quest Challengeapi-269630780100% (1)
- Oxford Reading Circle tg-4 2nd EditionDocument92 pagesOxford Reading Circle tg-4 2nd EditionAreeb Siddiqui89% (9)
- Computer Application in Chemical EngineeringDocument4 pagesComputer Application in Chemical EngineeringRonel MendozaNo ratings yet
- Research ProposalDocument18 pagesResearch ProposalIsmaelNo ratings yet
- 01ESS - Introducing Siebel ApplicationsDocument24 pages01ESS - Introducing Siebel ApplicationsRajaNo ratings yet
- Paediatrica Indonesiana: Sumadiono, Cahya Dewi Satria, Nurul Mardhiah, Grace Iva SusantiDocument6 pagesPaediatrica Indonesiana: Sumadiono, Cahya Dewi Satria, Nurul Mardhiah, Grace Iva SusantiharnizaNo ratings yet
- Uptime Elements Passport: GineerDocument148 pagesUptime Elements Passport: GineerBrian Careel94% (16)
- Abnormal PsychologyDocument13 pagesAbnormal PsychologyBai B. UsmanNo ratings yet
- OglalaDocument6 pagesOglalaNandu RaviNo ratings yet
- Nielsen & Co., Inc. v. Lepanto Consolidated Mining Co., 34 Phil, 122 (1915)Document3 pagesNielsen & Co., Inc. v. Lepanto Consolidated Mining Co., 34 Phil, 122 (1915)Abby PajaronNo ratings yet
- 28Document12 pages28physicsdocsNo ratings yet
- Barangay Sindalan v. CA G.R. No. 150640, March 22, 2007Document17 pagesBarangay Sindalan v. CA G.R. No. 150640, March 22, 2007FD BalitaNo ratings yet